基于多新息最小二乘算法的非线性系统辨识
2019-10-09刘芳芳任晓明
刘芳芳,任晓明
(1.国网河南省电力公司技能培训中心,河南 郑州 450051;2.中电科信息产业有限公司,河南 郑州 450050)
0 引言
最小二乘递推算法(recursive least square,RLS)是为解决传统最小二乘算法计算量大且不能在线辨识而产生的。其具有易于在线辨识,计算量小且简单易用的优点,备受学者和工程师的关注[1-2]。在线性系统和非线性系统的参数辨识中是应用较多的一种辨识算法。文献[3]利用一阶线性滤波技术对系统输入输出数据进行滤波,获得有效的辨识数据。通过采用递归最小二乘算法,辨识伪线性ARMA系统的各个参数。仿真结果表明了算法的有效性。文献[4]利用辅助模型设计了变递推间隔分解最小二乘算法。对比仿真结果证明了提出算法明显优于目前存在的一些算法。文献[5]针对输出误差模型辨识过程中计算负担大的缺点,利用分解技术将多变量系统分解为多个子系统辨识模型,然后通过对三个子系统分别设计递推最小二乘算法辨识各个子系统的参数。文献[6]提出的算法与常规的辨识模型不同,它利用装置瞬时能量状态而不是电荷状态作为燃料表的状态,然后构建辨识模型,利用递归最小二乘算法辨识超级电容器的电容和电阻值。试验验证了提出算法的合理性和有用性。
从上述文献可知,由于递推最小二乘法在每次参数更新时仅仅利用当前的系统信息,导致辨识精度较低和收敛速度慢,且递归最小二乘法应用于线性系统的辨识居多,用于非线性系统的辨识文献有限。因为递归最小二乘法(auxiliary model based least squares algorithm,AM-RLS)是根据线性系统的线性回归形式发展而来的,所以适用于处理线性系统。为此,多新息最小二乘法(multi-innovation least squares,MILS)通过利用p组数据改善了递推最小二乘的辨识性能。将多新息最小二乘算法尝试用于处理含输入非线性项的非线性系统辨识。在该算法中,利用关键项分离技术获得线性分离的辨识模型,减少了冗余的参数估计和计算负担。利用建立辅助模型解决内部变量未知问题,提高了辨识的精度。
非线性系统结构如图1所示。图1中:f(·) 为多项式非线性子环节;L(·)为动态线性子系统;v(t)为系统外加的噪声项;u(t)、y(t)为系统的输入、输出量;x(t)为中间变量。
这类组合系统以能够刻画一大类实际非线性系统
特性而受到研究者的关注[7-9]。

图1 非线性系统结构图
图1中,各个部分表达式为:
(1)
(2)
为了建立辨识模型,需要将非线性项代入线性子系统。如果直接代入,将导致辨识模型对各个参数是复合的,增加多余的参数估计。为此,当非线性项代入到线性项时,利用关键项分离技术[7-10]可以减少冗余的参数估计数量,同时减少了算法的计算负担。为获得唯一的辨识模型,一般设b1=1。
将式(1)代入式(2),结合关键项分离技术,可得:
y(t)=b1f1x(t-1)+b1f2x(t-1)2+…+b1fmx(t-1)m+b2x(t-2)+b3x(t-3)+…+bnbx(t-nb)-
a1y(t-1)-a2y(t-2)-…-anay(t-na)+v(t)
(3)
将式(3)化为紧凑的形式,表达式为:
y(t)=φT(t)θ+v(t)
(4)
其中,系统信息向量φ(t)的表达式为:
φ(t)={x[t-1,x(t-1)2,…,x(t-1)m,x(t-2),x(t-3),…,x(t-nb),-y(t-1),
-y(t-2),…,y(t-na)]}T
(5)
被估计参数向量θ为:
θ=[b1f1,b1,f2,…,f1fm,b2,b3,…,bnb,a1,a2,…,ana]T
(6)
1 辨识算法
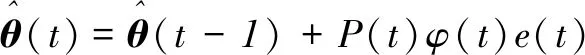
(7)
(8)
P-1(t)=P-1(t-1)+φ(t)φT(t)P(0)=p0I
(9)
在RLS算法中,e(t)为单新息。参数更新时仅仅利用了当前系统信息,这使得参数辨识性能不够理想。为了提高RLS的辨识性能,利用p组数据构造多新息向量。为此,定义:
φ(p,t)=[φ(t),φ(t-1),…,φ(t-p+1)]T
(10)
y(p,t)=[y(t),y(t-1),…,y(t-p+1)]T
(11)
则多新息向量E(p,t)可以表示为:
(12)
当p≥2 时,MILS算法表述为:

(13)
(14)
P-1(t)=P-1(t-1)+φ(p,t)φT(p,t)
(15)
为了避免求矩阵的协方差矩阵,结合矩阵求逆原理和式(13)~式(15),可以获得下式的多新息最小二乘法算法:
(16)
由于信息矩阵中含有未知的变量x(t),会使得辨识算法无法实施。为此,利用辅助模型辨识思想[11],构造如下的辅助模型。利用辅助模型的输出替代未知的变量,使辨识算法可顺利实施。辅助模型的表达式为:
(17)
为便于后续仿真对比,将提出的算法称为基于辅助模型的多新息最小二乘辨识算法(auxiliary model based multi innovation least squares algorithm,AM-MILS)。
当新息长度p=1时,MILS简化为最小二乘的形式,即:
(18)
2 仿真结果
为了验证提出算法的优势,将基于辅助模型的AM-RLS[12]作为对比仿真。
考虑系统为:
x(t)=0.5u(t)+0.2u2(t)+0.1u3(t)
y(t)=u(t-1)+0.2u(t-2)-0.6y(t-1)-0.45y(t-2)
此系统中真实的参数为f1=0.5,f2=0.2,f3=0.1,b1=1,b2=0.2,a1=0.6,a2=0.45。本文的目标是利用可测的输入输出数据,设计辨识算法,以辨识这些真实的参数值,并验证辨识算的有效性。
AM-MILS的初始参数为:p0=106,θ(0)=[0.001,0.001,0.001,0.001,0.001,0.001]T,N=2 000,p=4,噪声为白噪声,输入幅值为1的随机序列。对比算法AM-RLS的初始值参数和AM-MILS 一样。不同算法多项式参数估计曲线、不同算法线性子系统系数参数估计曲线如图2、图3所示。
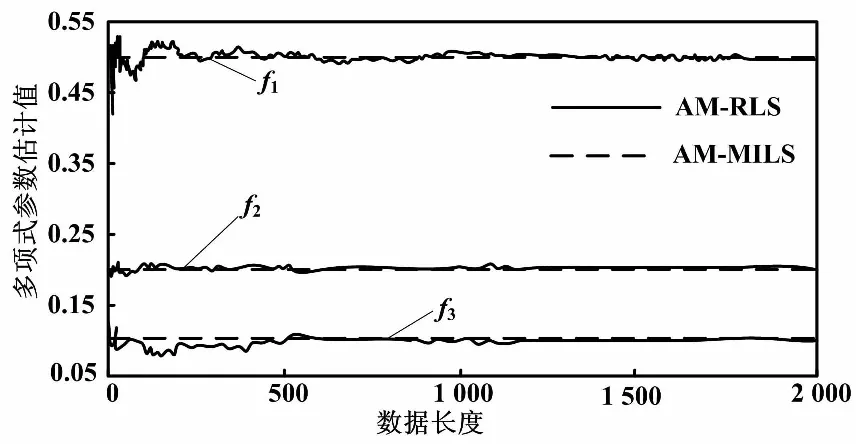
图2 不同算法多项式参数估计曲线
从图2、图3可以看出,在参数估计的初始阶段,两种辨识算法的估计曲线都快速向真实值靠拢,在参数估计的后期阶段,随着数据的增加,被估计的参数能够收敛于真实值或其附近值。这说明两种辨识算法对这类非线性系统是有效的。但是从图2、图3中也可以看出,AM-RLS 参数估计结果有明显的震荡,且收敛速度明显低于AM-MILS算法,这主要得益于AM-MILS通过利用p组系统信息,不仅利用了当前的数据而且利用过去的信息,提高了辨识的性能。

图3 不同算法线性子系统参数估计曲线
图4是AM-RLS模型验证结果,图5是AM-MILS 算法模型验证结果。

图4 AM-RLS模型验证结果
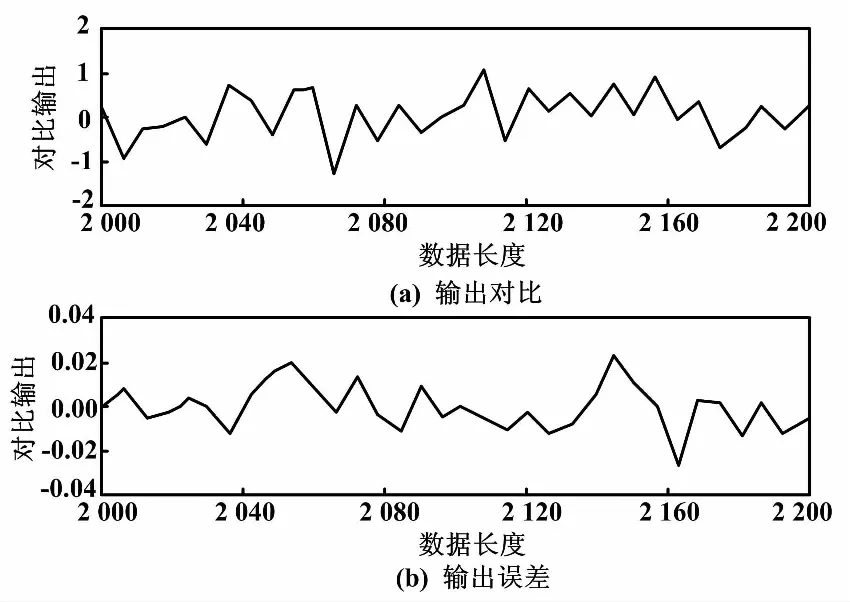
图5 AM-MILS模型验证结果
从图4和图5可知,基于两种辨识的算法建立的估计模型都能有效地跟踪实际模型的输出。这说明辨识结果是正确的、有效的。基于AM-MILS算法的模型相对于AM-RLS算法而言能够以较小的输出误差跟踪实际模型的输出,这说明AM-MILS的辨识性能高于AM-RLS算法,这和参数估计结果图2、图3是一致的。
参数估计误差曲线[11-13]如图6所示。图6显示两种辨识算法的参数估计结果都是随着数据的增加而逐渐减少的,最后趋向于一个较小的平稳值。但是图6也反映了AM-MILS算法比AM-RLS 算法有更高的估计精度和收敛速度,侧面证明了AM-MILS的优势。

图6 参数估计误差曲线
从图6可以得出一个结论:AM-MILS因为引入了多新息长度,使得辨识性能高于AM-RLS算法。
3 结束语
本文针对含输入非线性项的非线性系统辨识问题,将多新息长度引入到单新息中,设计多新息向量。基于多新息最小二乘法,实现考虑系统的参数辨识。构造的辨识模型对参数向量是线性的,有效避免了多余的参数估计并减少了计算量;辅助模型的建立解决了未知的中间变量问题,提高了参数辨识的精度。对比结果表明,相比于基于辅助模型的递推最小二乘算法,基于多新息最小二乘算法的辨识结果更接近真实值,更能描述实际模型的输出非线性特性。这证明了加入多新息后,设计的辨识算法的辨识性能变得更加优异。
