浅谈异形盾构三刀盘同步控制方法
2019-10-09黄圣
黄圣
(上海隧道工程机械制造分公司,上海 200137)
1 研究背景和目的
1.1 项目背景
在异型盾构的制造技术中,异型断面的切削组成形式有很多种选择方案,通过土压平衡型盾构机在施工过程中对前方土体的扰动影响分析中发现,全断面切削可以使土体的扰动达到最小,经过全断面异型盾构设计可行性研究,及对多动力源驱动大刀盘扭矩平衡控制系统的掌握,提出了以3 个圆形大刀盘在一工作面上进行大断面切削的刀盘驱动模式。同一平面上的左中右3 个大刀盘的运转轨迹有部分重叠,如图1。

图1 三刀盘结构
由于切削面在同一个平面上,如果控制不当,可能会产生左中,中右刀盘互相干涉的情况,造成刀盘损坏,这对工程的正常施工和设备的维护会带来非常严重的影响,故需要研究一种具有高可靠性的控制方法,避免同一平面上3 个刀盘在运转时的互相干涉,从而使3 个刀盘能在异型断面内进行全断面的连续的切削。
1.2 原有多刀盘控制技术
在市场上,三圆盾构本身比较少见,而且一般异性多刀盘盾构机一般的切削面会选择设计在不同平面上,很难找到可以参考的产品。多刀盘的角度差控制一般根据盾构机的刀盘形式,在双圆盾构中运用的比较广泛,其代表产品有日本三菱重工和石川岛播磨,于2004 年在国内应用于上海轨道交通的区间隧道施工中,其对多刀盘同步角度差的控制比较简单,是根据角度差控制的边界条件来进行刀盘运行的强制停止,而在上海隧道的类矩形盾构机的中运用的同步控制方式,可以动态的控制两个刀盘的角度差,在控制性能上有着显著的提升。
1.3 研究目的
通过对原有的双刀盘同步控制系统进行研究,依据目前多刀盘的结构特点和施工要求,为了增加施工的连续性和可靠性,需要研究一种在掘进过程中能动态的、实时的对角度偏差进行同步控制的三刀盘同步方法。
2 同步控制系统模型
2.1 刀盘驱动方式选择
一般刀盘的驱动形式有着油马达,双速电机加离合器和变频器两种驱动形式,油马达形式的大刀盘驱动有着负载平衡响应快的特点,但其调速性能比较差。双速电机加离合器的驱动方式无法对刀盘速度进行微调。变频驱动的方式既能通过对刀盘电机的机械特性软硬度的调整达到负载均衡的目的,又可以通过频率的调整对多刀盘的速度控制进行微调。故选择使用变频驱动方式作为大刀盘的动力源。
相对于其他两种驱动方式,变频驱动可以通过软件方式对3 个刀盘分别进行分段的加、减速控制。并能在紧急状态下通过刹车电阻实现快速制动功能,来保证刀盘启动和停止过程的安全性。同时在3 个刀盘运行过程中可以通过快速的偏差响应,对运行中产生的角度偏差进行实时调整。
2.2 控制模型
三刀盘旋转同步修正,不同于双刀盘的同步修正,因为存左中,中右两种可能干涉的刀盘关系,如果作为整体系统进行考虑,那就有三个刀盘转速三个控制变量及两个角度差两个控制目标,控制模型会非常复杂。在这个项目中,我们对控制系统进行简化,讲中间的刀盘从控制系统中剔除,其作为开环控制,根据设定频率进行旋转,而其他左右两个刀盘的转速通过于主刀盘角度的差值计算进行闭环控制,这样就把一个复杂的系统分解为简单的左中,中右两个只有一个控制量和一个控制目标的控制模型。显然这样的控制模型更好在系统内搭建及运行。
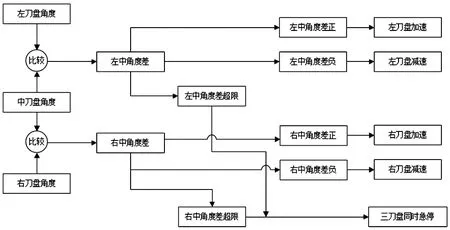
图2 刀盘角度控制系统图
在3 个圆形大刀盘驱动装置的中心位置安装刀盘位置、速度检测装置,就可以实时测定三个刀盘的转速和角度。采用在变频器中设定的加速时间和分段加速的方式,保证刀盘启动期间运转的安全。在三个刀盘运转期间,通过专用控制算法和手段,实时计算三刀盘角度差后通过防干涉的算法来及时调整刀盘转速,从而保证刀盘不发生相互干涉,并确保刀盘扭矩的同步,如图2 所示。
在刀盘停止期间,通过可控的制动方式及刀盘角度的实时反馈来控制刀盘快速停止在预定的位置上,并且保证了两刀盘之间安全的角度差,如图3 所示。

图3 双刀盘停止控制系统图
2.3 控制方式选择
多刀盘的同步控制从控制形式上看是一个运动系统,其控制的刀盘的转速这一向量及多刀盘之间的角度差;由于其运动空间受限,为多个重叠的刀盘切削面,并且其速度方向的限制,只是旋转速度。故并不需要进行运动学的一些计算,可以简化为一种过程控制来进行分析。
选择工程上经常使用的PID 控制器,主要原因有两点,首先是PID 控制是一种非常成熟的控制方式,其次现有的主流可编程序控制器都带有PID 控制模块,可以使整个控制流程都集成在系统本身的硬件中,不需要再经过运动控制器进行运算处理。
在PID 控制算法中,其输入e(t)与输出u(t)的关系为:
u(t)=kp[e(t)+1/TI ∫e(t)dt+TD×de(t)/dt]
式中积分的上下限分别是0 和t。
因此它的传递函数为:
G(s)=U(s)/E(s)=kp[1+1/(TI×s)+TD×s]
其中kp 为比例系数;TI 为积分时间常数;TD 为微分时间常数。其工作原理如图4 所示。
图中r 为设定值,y 为输出值,e 为两者之间的误差,通过MatLab 仿真,可以得到一个经典的PID 控制输出的曲线,如图5 所示。
图5 是一个比例常数为2,积分常数为20,微分常数为1 的PID 控制系统,我们可以看到,在有小幅震荡后系统很快自动达到了系统的设定值。这符合对双刀盘同步驱动系统的控制要求。
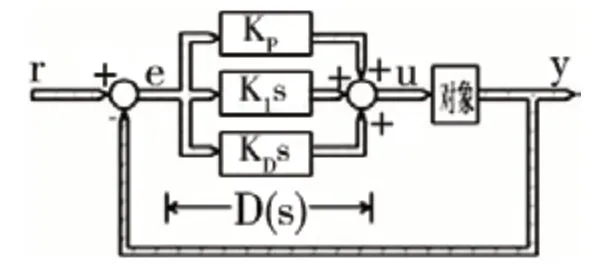
图4 PID 控制系统图
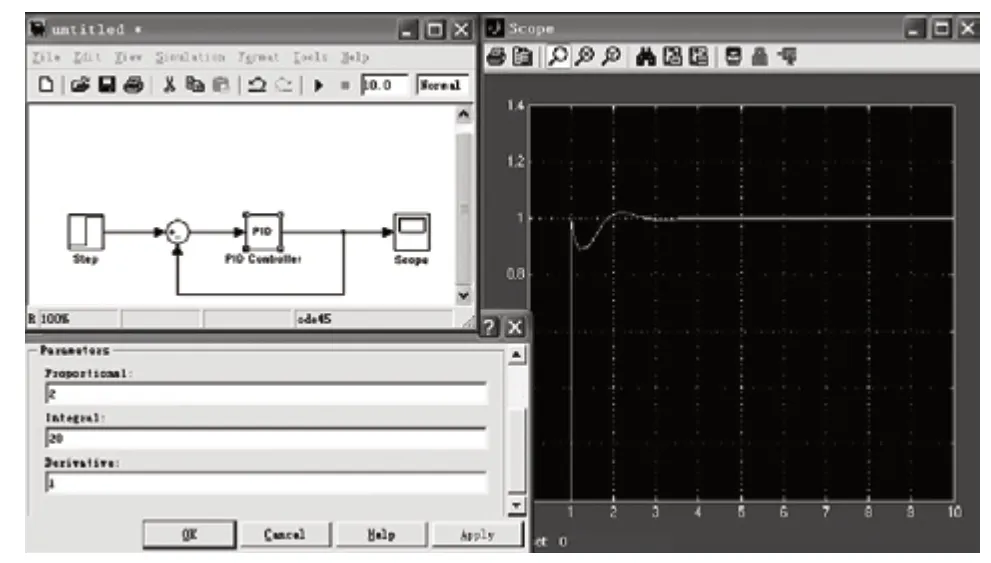
图5 Matlab PID 仿真
2.4 控制系统的组态
根据所确定的刀盘驱动型式、控制模型和控制方法,具有偏差同步控制的系统框图如图6 所示。
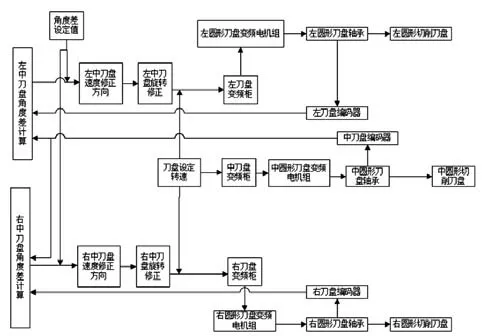
图6 三刀盘控制系统组态
3 结语
通过上述研究,可以得到一个对于同一切削平面的三刀盘同步控制系统,该系统可以对在同一切削平面上相互干涉的三个刀盘进行控制,达到保持系统平衡,避免干涉的效果。
