例谈数形结合思想在一次函数教学中的运用

陈璐

【摘 要】数学是研究数量关系和空间形式的学科，其所研究的范围和对象决定了“数形结合”是学生学习过程中，不可或缺的一种思想方法，尤其是在初中一次函数教学中，很多问题都需要学生从“数”和“形”两个方面做出思考，因此在教学过程中，教师能够将数形结合思想渗透于其中具有重要意义，下面笔者将从自身的实践教学经验出发，做出相关介绍阐述。

【关键词】数形结合思想;一次函数;教学运用

【中图分类号】G633.6       【文献标识码】A

【文章编号】2095-3089（2019）18-0235-02

前言

在整个初中阶段的数学学习中，函数学习具有极其重要的地位，并贯穿于学习始终，而一次函数是学生学习认识函数的开端，是学生学习二次函数、反比例函数的基础，在一次函数教学中，教师要明确数学思想是数学学科的灵魂，是学生学好数学知识的关键，而函数是“数”与“形”的巧妙结合，将数形结合思想运用到一次函数教学中，可更好的助力学生数学学习成长。

一、数形结合思想及一次函数介绍

1.数形结合思想。

数学领域之中有这样的一句话“数无形，少直观，形无数，难入微”，由此可以看出，在数学学科之中，“数”与“形”是不分家的，数形结合是学习数学最基本也是最有效的一种方法[1]。简而言之，数形结合可理解为以数学问题的条件和结论为内在联系依据，分析代数意义的同时，揭示几何直观意义的一种方法。在学习数学学科的过程中，数形结合大致可以分为两种情形，一是“以数解形”，即借助数的精确性，对形的属性做出阐述;二是“以形助数”，即借助几何的直观性，阐述数字之间的某种联系。在数学领域之中，如解函數问题、方程问题、绝对值问题、立体几何问题等，数形结合思想都是非常适用的，而纵观近几年的中考命题趋势，也十分注重学生对数形结合的掌握考察，因此在日常教学中，教师能够在课程知识讲解时，潜移默化的将数学知识应用其中，这对学生的数学学习发展是有诸多裨益好处的。

2.一次函数教学。

“一次函数”是初中数学的核心内容，也是重要的基础知识内容，与未来高中阶段的知识有紧密的联系，同时还在现实生活之中广泛应用，研究学习一次函数，一定要把定义、性质、图像紧密的结合在一起，这样学生才能体会知识的真谛，掌握解题的要领[2]。（1）函数的定义，一个量随着另外一个量的变化规律。这里后一个量就是自变量，前一个量因为后一个量的变化而变化，所以叫因变量，自变量的取值范围，与函数的整式、分式、根式具体表达方式有关，要使这些式子有意义。（2）一次函数的定义，表达形式为y=kx+b，其中k、b是常数，k不等于0。

二、数形结合思想在一次函数教学中的运用

1.以形助数，直观理解函数图像性质。

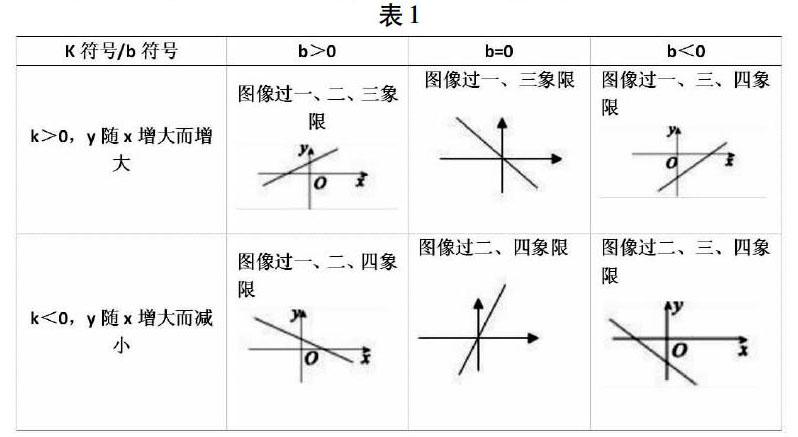
在初中数学“一次函数”课程教学中，教师要从基础知识抓起，强化学生对一次函数图像性质的掌握，这样才能为学生的后续学习典型基础，而显然在这个过程中，单依靠“数”的讲解是远远不够的，只有采用数形结合的方法，借助图形的直观性将抽象的数学概念和数量关系形象化，这样才能帮助学生在头脑之中构建数学模型，为学生的概念形成理解奠定基础。具体而言，教师在向学生讲解一次函数图像性质时，可以为学生出示下表：

在该表之中，将“数”与“形”完美的结合在了一起，一次函数知识不再是空洞无物的，函数知识有了具体的形象，在“以形助数”的过程中，学生对一次函数图像知识有了更加深刻的认识和理解[3]。

2.以数解形，借助性质强化图像功能。

在初中数学“一次函数”课程教学中，函数图像形象的显示了函数的性质，为学生认识学习一次函数提供了“形”的直观基础。同样，一次函数关系式，是由“数”构建的，数赋予了图像的基本形式，因此在运用数形结合思想时，“以数解形”也是一种可行的教学方式，可使问题便的一目了然。以这样的两个问题为例：

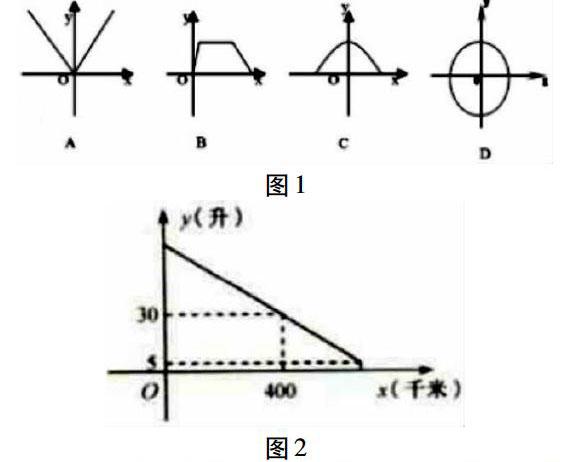
例1：“下列四个图像之中，表示某一次函数的图像有哪些？”

在这一函数问题之中，就需要采用“以数解形”的方式进行解题，如要从数形结合的方向思考，依据函数图像在自变量x的取值范围内任取一个值的一次函数定义，可以发现，在上述出示的四个图像之中，A、B中的变量y都有与之相对应的值，因此A、B都可称之为一次函数，而C、D图像之中，变量y不是x的唯一变量，因此不能表示某一函数的图像。在这一数学问题之中，就充分的体现出了“以数解形”的重要作用。

例2：2018年中考试题中有这样的一个解答题：一辆汽车行驶时的耗油量为0.1升/千米，如图是油箱剩余油量y（升）关于加满油后行驶的路程x（千米）的函数图形（如图2所示）。（1）根据图像直接写出汽车行驶400千米时的油箱内剩余油量，并计算加满油时油箱的油量。（2）求y关于x的函数关系式，并计算该汽车在剩余油量5升时已行驶的路程。

解答：对于这一问题，通过题意可知，汽车行驶400千米剩余油量30升，加满油时油量为70升;在对（2）问题解析时，可设y=kx+b（k≠0），把点（0，70），（400，30）坐标代入得b=70，k=-0.1，故y=0.1x+70，而当y=5时，x=650，得出汽车已行驶路程为650千米。通过这样的一个函数问题，在解一次函数问题时，要从形到数，量化入微，在充分理解题意的基础上，仔细的观察分段函数的特征，这样才能确定最终的函数解析式。

3.数形结合，实现方法到思想的飞越。

在初中数学“一次函数”课程教学中，数形结合思想的运用，不仅是“以形助数”或“以数解形”，还应该做到数形结合，将“数”与“形”结合在一起进行思考，通过把数量关系问题转化为图形问题，或者通过将图形问题转化为数量关系问题，从而实现从“方法”到“思想”的飞跃，这样才能将函数问题简单化，抽象问题具体化，最终实现高效学习、高效解题的目标[4]。函数知识是贯穿于整个初中阶段的学习内容，而一次函数是学生函数学习的开端和基础，因此学好一次函数知识尤为重要，但显然在笔者执教的过程中发现，对于函数问题，很多学生感到望而生畏，函数学习成为无法攻克的难题，而函数本就是“数”与“形”的巧妙结合，在解题的过程中，可以充分的借助数形结合思想，同时将函数问题与方程、不等式相关知识联系在一起，善于将知识“牵手”，将“形”与“数”对应在一起，这样很多复杂的问题就会迎刃而解、不攻自破，这是新课标背景下，教师需要树立的一种教学思想。

4.数形联系，函数建模中强化数形结合。

在初中数学“一次函数”课程教学中，数形结合思想的运用，可以借助一次函数的图像，直观的分析一元一次方程的解、不等式解及二元一次方程组的解，在这个过程中，学生就可以体会到函数解与图像点坐标之间的紧密联系，从而品味到数学学科之中，数形结合的魅力，同时借助数形之间的巧妙联系，还可以帮助学生在脑海之中构建数学模型，这对学生的数学学习发展都是十分具有裨益好处，而这也是一次函数中渗透数形结合思想的主线，举这样一个例子，如下表所示，移动公司推出了两种话费套餐方式，问选择哪种计费方式更加省钱？

在面对这一问题时，可将通话时间设为x，月消费用为y，那么全球通的函数解析式就为y=50+0.4x，而神州行的函数解析式则为y=0.6x。运用数形结合思想，可在同一坐标系之中，画出这两个函数解析式的图像，可以发现x=250，y=150时两函数之间存在交点，因此通过对图像的观察可以发现，在通话时间为250min之前，神州行套餐资费是更加合适的，在通话时间刚好为250min时，两种套餐价格相同，而当通话时间超出250min时，全球通套餐则更加经济实惠。在初中数学“一次函数”课程教学中，教师要善于借助数与形之间的联系，帮助学生在头脑之中建立函数模型，而这将转化为一种能力，推动学生的函数学习更进一步。

5.数形与实际结合，避免教学误区出现。

一次函数在现实生活之中有广泛的运用，如购买消费活动中，生产加工活动中，都会涉及变量与线性之间的关系，这时就可以借助一次函数去解决问题，因此数形结合思想在一次函数教学中的运用，还应该强化生活实际与一次函数之间的有机结合，要借此培养学生运用函数知识解决生活问题的能力，防止出现“一次函数都是一条直线的误区”。举这样的一个例子，如发动机开始工作时，初始油箱之中有40L的机油，每小时消耗5L，求邮箱剩余有油量q与工作时间t之间的函数关系，试画出其中的函数图像。在解答这一问题时，若是只有数，而无形，就很容易出现解题错误，而数形与实际相结合，就可以更加准确的观察出函数q=-5t+40在0≤t≤8这个区间内，是一条线段而不是直线，这是因为油箱之中的机油是会消耗尽的，因此解一次函数生活性问题时，要从生活实际出发，兼顾数形，注意自变量的取值范围，从而画出标准的一次函数图像[5]。此外，在实际生活问题之中，“最值”一般都是指“最高成本”“最高利润”“最少之处”等，大部分情况下，自变量的取值范围是全体实数，但也有一些自变量受实际限制。

总结

在初中数学教学中，一次函数是十分重要的教学内容，贯穿渗透于学生的整个数学学习生涯中，而数学思想方法是数学知识的灵魂，是学生学好数学学科的关键，在一次函数教学中，教师能够将数形结合思想方法渗透于其中，这可以帮助学生更好的领悟到函数的真谛，并迅速的掌握函数的解题要领，因此的今后的一次函数函数教学中，教师有必要关注对数形结合思想的运用研究。

参考文献

[1]柴文甲.例谈数形结合思想在一次函数教学中的运用[J].青海教育，2019（03）：47-48.

[2]胡诗雨.初中数学课堂渗入数形结合思想——以一次函数与二元一次方程的关系为例[J].中学数学研究（华南师范大学版），2017（20）：20+17.

[3]朱根陆.数形结合有妙用以图思图建奇功——例谈一次函數的图像问题[J].中学数学，2017（22）：78-79.

[4]余敬平.结合函数图象解决行程问题——数形结合思想在一次函数中的应用[J].初中数学教与学，2016（10）：39-41.

[5]潘红涛.谈数形结合思想在一次函数中的应用[J].数学学习与研究，2016（15）：101.