脐动脉血流信号非线性临床研究

俞凯君 许子非 李春

摘  要： 针对孕妇脐动脉血流信号确定性与随机性相结合的复杂非线性特征，从一个新的角度研究正常与病态血流信号间的差异。首先以孕妇真实的临床诊断数据为研究对象，分析了超声脐动脉血流信号的搏动指数、阻力指数及S/D值，并分析了其健康状况，在此基础上引入分形维数对非线性脐动脉血流信号进行对比研究。通过分析孕妇脐动脉血流分形维数，分析异常脐血流信号的分形特征，结果表明：分形维数与孕周具有相关性，分形维可作为定量检测孕妇及胎儿健康状况的重要指标。

关键词： 脐血流信号;搏动指数（PI）;阻力指数（RI）;S/D值;分形维数

中图分类号： R318; N93    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2019.04.035

本文著錄格式：俞凯君，许子非，李春. 脐动脉血流信号非线性临床研究[J]. 软件，2019，40（4）：162167

【Abstract】： Aiming at the complex nonlinear characteristics of determinate and randomness of umbilical arterial blood flow signals in pregnant women， the difference between normal and abnormal blood flow signals is studied from a new perspective. Firstly， the actual clinical diagnosis data of pregnant women were taken as the research object. The pulsation index （PI）， resistance index （RI） and S/D value of ultrasound umbilical artery blood flow signal were analyzed， and their health status was analyzed. A comparative study of nonlinear umbilical arterial blood flow signals was performed by using fractal dimension. The fractal dimension of umbilical arterial blood flow and the fractal characteristics of abnormal umbilical blood flow signal were analyzed.The results showed that fractal dimension is correlated with gestational age and it can be used as an important indicator for quantitative detection of pregnant women and fetus health status.

【Key words】： Umbilical blood flow signal; Pulsation index （PI）; Resistance index （RI）; S/D; Fractal dimension

0  引言

脐动脉是母体向胎儿传递营养和物质的重要通道[1]，对孕妇脐动脉的血流信号进行采集和分析，可获取有关胎儿生长发育的重要信息[2]。目前，超声多普勒技术已广泛应用于产科的临床诊断中以获取胎儿发育的相关信息，通过对这类信息的分析及处理，尽早发现胎儿异常以便及时处理，提前治疗以降低先天性疾病概率、提高生育质量。

多普勒脐动脉血流信号属于典型的非平稳信号，具有复杂的时变特征。传统的脐动脉多普勒血流信号的分析方法主要有声谱参数法和波形分类法。

声谱参数法是通过获取声谱参数数值大小，判断脐血信号是否异常。常见的声谱参数主要有收缩期血流速度最大值和舒张末期血流速度值之比S/D、搏动指数PI和阻力指数RI等。如，Hima[3]对比分析了正常和患有宫内生长迟缓（IntraUterine Growth Retardation，IUGR）孕妇的脐动脉和大脑中动脉多普勒血流信号，计算其声谱参数，发现在探测IUGR病症方面，脐动脉血流信号效果更好;Blanco等[4]通过脐动脉多普勒血流信号的声谱参数，发现脐动脉多普勒血流信号能检测妊娠异常，为胎儿健康评估提供有效信息;Dai等[5]发现患有急性胎儿宫内窘迫症孕妇脐动脉血流超声波的声谱参数S/D、PI和RI值更低。

波形分类法则是通过对大量病例的统计分析，将正常波形和各种不同程度典型病例分为数类。基于波形匹配，从各种分类决策法中找出最相似的波形作为匹配结果，以此作为诊断结果[5]。Malcus等[6]针对脐动脉多普勒流速波形图，提出一种新的半定量波形自动分类决策方法，并与临床数据进行对比，表明该方法有一定的临床应用价值;Latifoglu等[7]采集25位孕期13-40周孕妇脐动脉血流多普勒信号，基于短时傅里叶和自回归建模方法得出其功率谱密度图，发现孕妇怀孕初期的功率谱密度频率范围低于怀孕晚期;文献[8]在研制的彩色编码血流声谱图上，通过计算多普勒信号的最大频率自动提取声谱图的包络，然后自动实现一种波形的分类决策方法，从而为医学临床提供了一定的诊断标准。

但血流信号的频谱并未包含所有生理、病理特征信息，有许多富有极高价值的信息隐含在信号的相位谱中。仅通过分析信号频谱或时间波动规律尚不能进行准确的诊断。因此，选择一种更准确的非线性信号处理方法，对于脐血信号分析和孕妇、胎儿健康状况检测具有重要意义。

分形是解决非线性问题的一门重要学科，近年来相关研究十分活跃，其在化学、工程、生物、材料及医学等领域均取得了良好的应用效果，尤其是生物医学信号处理方面[6-12]。国内外相关研究人员已应用分形理论处理多种类型的非线性信号，如生物信号检测与指标提取、图谱分析与辅助功能诊断、心率变异性研究及蛋白质二级和三级结构预测   等[13-16]。Sladana[17]通过分形理论处理脑电波数据，通过计算脑部受伤前后脑皮层信号的Higuchi分形维数，发现脑部警觉性变化将会改变脑电波信号的分形维数;文献[18]采用Imagej方法分析腰椎体松质骨区域图像，腰椎松质骨CT图像灰度纹理信息的分形维数可量化骨微结构的退变程度，说明分形理论可基于CT图像进行定量的医疗诊断;Bogaert等[19]分析了正常人与心脏移植患者的心率變异信号的关联维数，研究表明心率变异信号的关联维数可以清楚地反映性别和生理差异;文献[22]研究了受试者麻醉期心率变异性信号的关联维数与尺度指数等分形特性参数，结果表明麻醉期心搏周期具有明显的分形特性变化。

以上研究说明，分形理论可以通过分析脑电波、动脉多普勒血流信号和CT图像等典型的医学非线性特征，获取不同医学信号的隐含信息，从而对案例进行科学诊断。与传统声谱参数法和波形分类法相比，分形理论具有更强大的非线性信息处理能力，可更为全面、透彻地反映信号的深层次信息。

为此，本文在超声多普勒信号分析的基础上引入分形维数对非线性脐动脉血流信号进行对比研究。通过分析孕妇脐动脉血流分形维数，从一个新的角度研究正常与病态血流信号间的差异，并分析病态血流信号的畸变特征和病理特性。

1  分形维数计算原理及方法

1977年，哈佛大学教授B.B.Mandelbrot首次提出“分形（Fractals）”一词;1986年，将部分与整体以某种形式相似的形体定义为分形[21]。分形具有自相似性、标度不变性、存在分数维数以及整体与局部、局部与局部具有长程相关性等特点[22]。分形维数是定量分析研究对象自相似性的一种度量参数，其计算方法有多种[23]。其中，计盒维数法原理简单，易于实现，因此，成为应用最广泛的方法之一[24]。

2  脐血流多普勒信号的临床意义与采集

2.1  脐血流信号的临床意义

常用脐动脉测定数据指标有S/D值（收缩期最高峰值/舒张末期低峰值）、搏动指数PI（PI=（SD）/ M，M为频率变化均值）、阻力指数RI（RI=（SD）/S）。上述指标可直接反应血流波形在收缩期和舒张期的形态，虽然可以不依赖于声波和血管的夹角，但这些波形受胎儿呼吸运动、胎心率变异、孕妇体质等因素影响。例如，孕妇仰卧位时，脐血流阻力增加等。

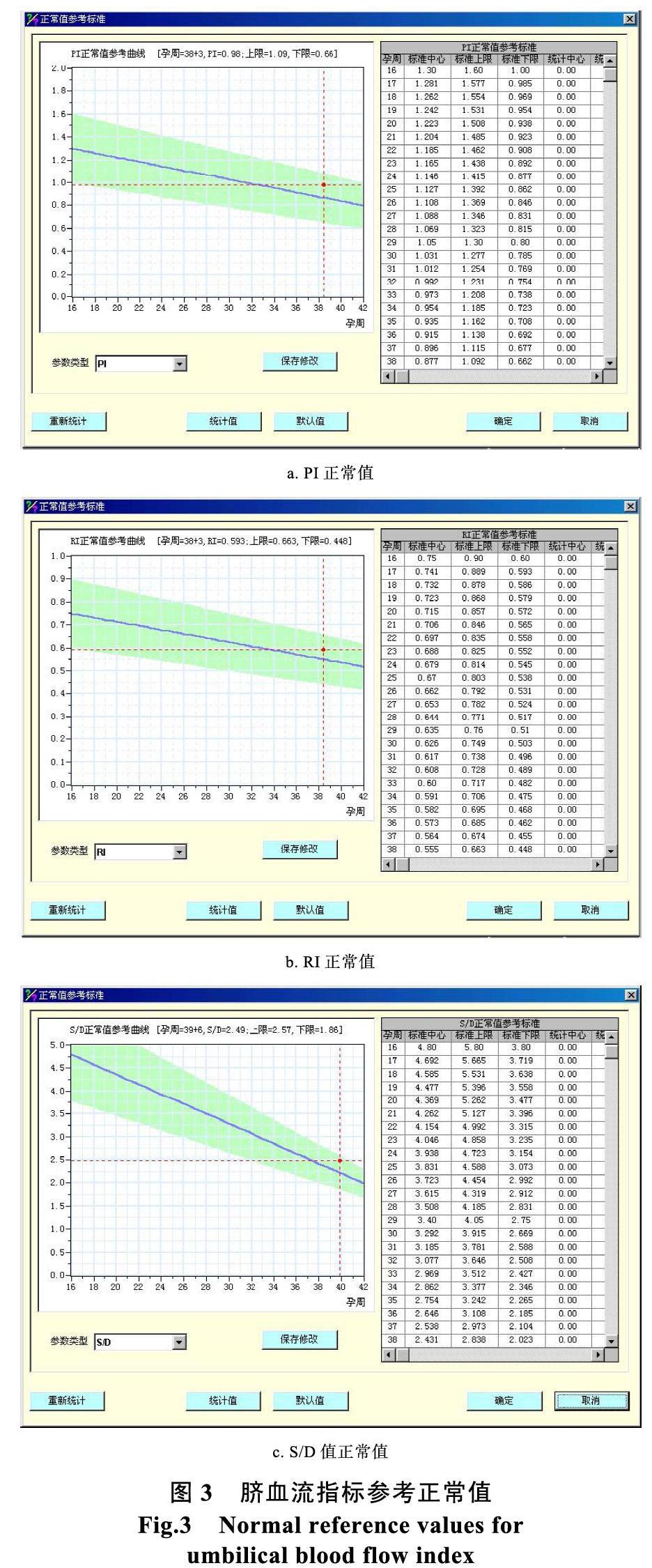
临床研究表明，对于处于不同孕周的健康孕妇及胎儿，脐血流信号的PI值、RI值及S/D值均有其正常的合理区间值。临床诊断中将通过多普勒血流信号采集仪采集到脐血流信号与PI、RI及S/D的正常值参考曲线图谱及参考标准进行比较分析，最终以此判定胎儿及孕妇的健康状况。脐血流信号各参数值的正常值及其健康区间范围如图3所示。

由图3可知，健康的孕妇的胎儿PI值应介于0.6～2.0之间，RI值介于0.4～1之间，S/D值介于2～4之间。在正常情况下PI值、RI值及S/D值均随孕周增长而逐渐下降。30孕周时PI值降至0.8～1.2，RI值降至0.5～0.75，S/D值降至小于3。在孕周增长过程中，S/D值下降，说明血流阻力在逐渐降低，血流增加，这有利于胎儿的生长和发育。当以上各指标不在健康合理区间范围内时，通常表现出各种症状，比如RI过高，表明胎儿-胎盘、子宫-胎盘的循环阻力增高，临床表现为妊高症病理特征;再比如S/D值异常升高，通常与母体血清葡萄糖含量有关，所以S/D比值监护可作为控制血糖水平的一项指标。通过以上参数还可检测胎儿是否发育迟缓、双胎、早产、羊水过多与不足及脐带异常等症状。

2.2  脐动脉血流信号的采集与分析

数据来源于无锡市锡山区人民医院鹅湖分院临床实验，实验设备为多普勒血流信号采集仪，型号为EDAN-MFM-OBM。该设备采集脐动脉血流信号的原理是：利用多普勒效应，声源以固定频率发射超声波，超声波遇到界面发生反射。用于测量血流时，声源发射的超声波在流动的红细胞上可发生后向散射，发射信号与反射信号的多普勒频移会发生改变，将这种改变的数据进行比较，用于测量血流方向和速度。多普勒血流信号采集仪的采集窗口如下。

根据上述脐血流信号采集原理，对处于不同孕周的104位就诊孕妇进行了多普勒信号采集，获取了多普勒信号图谱，如图5为某孕妇30孕周时的脐动脉血流信号图谱。此外，记录并分析了每个孕妇的搏动指数（PI）、阻力指数RI及S/D值，结果如6所示。

由图6可知，本文选取的104位孕妇孕周为26周至42周，年龄介于22岁到43岁之间。对104位孕妇脐血流信号进行临床诊断分析，其中61位诊断为正常，其余43位异常或存在疑问。根据搏动指数诊断有14位孕妇的PI值出现异常，其中4位孕妇PI指数偏高，初步表面脐带可能受到外界挤压动脉血流不畅，容易造成胎儿营养不良;另外10位PI指数偏低，将表现出其他临床症状。根据阻力指数诊断，有18位孕妇脐血流信号异常，主要表现为脐带流阻偏低。根据S/D值分析，有28位存在异常，初步诊断为母体血糖异常。

3  脐动脉血流多普勒信号分形维数分析

根据分形维数计算分析原理，对104位孕妇脐血流信号图谱进行分形维数分析，为使结果更加准确，分别对每位孕妇不同心动周期下脐血流信号图谱进行分形维数计算，然后计算其平均值作为该孕妇脐血流信号的最终分形维数。

首先对61位健康孕妇脐血流信号图谱的分维值计算与分析，结果如图7所示。

由图7结果可知：正常孕妇脐血流信号的分形维数介于1.718～1.776之间，分形维数与孕周之间具有相关性，随孕周的增长，分形维数总体呈增大趋势。究其原因为：随着胎儿逐渐增大，所需营养增多，脐动脉血流量增大，同时血流复杂性增大，因此分形维数有增大趋势。

然后对43位异常或存疑孕妇脐血流信号图谱的分维值计算与分析，结果如图8所示。

由图8结果可知：异常或存疑孕妇脐血流信号的分形维数介于1.753～1.901之间。总体趋势与正常孕妇脐血流信号的分形维数趋势相似，分形维数随孕周增大也呈增大趋势。

对比图7与图8可知，总体上正常孕妇脐血流信号的分形维数较异常/存疑孕妇脐血流信号分形维数小。究其原因为：健康孕妇脐血流流量更加稳定，胎儿呼吸均匀，因此其多普勒信号更加稳定;而异常孕妇因存在病例上的不正常狀况所致，母体为胎儿的供血不稳定或是胎儿呼吸不稳定等因素造成多普勒检测信号波动较大，因此其分形维数较大。根据以上分析表明，孕妇脐血流信号具有分形维数，且分形维数与孕妇孕周存在相关性，表现为孕周越长分形维数越大;孕妇脐血流信号的分形维数与孕妇与胎儿的健康存在相关性，分形维数可定量检测孕妇脐血流流动的稳定性。

4  结论

基于上述研究与分析，主要结论如下：

（1）孕妇脐动脉血流信号的分形维数与孕周具有关联性，孕周越大分形维数越大;

（2）孕妇脐血流信号的分形维数与孕妇与胎儿的健康状况有关，分形维数可作为定量监测胎儿健康状况的指标。

（3）脐动脉血流信号的分维值在一定程度上反映母体对胎儿供血情况，具体表现为：健康孕妇脐动脉血流多普勒信号分形维数总体较异常孕妇脐动脉血流信号分形维数低，表明正常孕妇脐血流流动更稳定，而异常孕妇脐血流波动更剧烈。

参考文献

[1] Trudinger B J， Giles W B， Cook C M. Flow velocity wave-forms in the maternal uteroplacental and fetal umbilical placental circulations[J]. American Journal of Obstetrics and Gynecology， 1985， 152（2）： 155-163.

[2] 张振钧， 王宏. 超声多普勒脐动脉血流测定的探讨[J]. 中华妇产科杂志， 1990， 25（4）： 212-214.

[3] Blanco P G， Vercellini R， Rube A， et al. Evaluation of Feline Uterine and Umbilical Arteries Blood Flow in a Pharma-cologically Induced Abnormal Gestation Model[J]. Therioge?no?logy， 2016， 86（9）： 2323-2327.

[4] Latifoglu F， Kara S， Guney M. Spectral Analysis of Umbilical Artery Doppler Signals During Normal Pregnancy Using STFT and AR Method[C]. IEEE： International Sym-posium on Signal Processing and ITS Applications， 2007.

[5] 吴晓峰， 汪源源， 王威琪， 等. 对超声DOPPLER声谱图进行分类决策的两种方法[J]. 应用声学， 1996， 11（3）： 7-11.

[6] Xia Shaoxu， Yao Bin， Chen Qiping， et al. Composites with Koch Fractal Activated Carbon Fiber Felt Screens for Strong Microwave Absorption[J]. Composites Part B Engineering， 2016， 105（11）： 1-7.

[7] Cai Wei， Chen Wen， Xu Wenxiang. Characterizing the Creep of Viscoelastic Materials by Fractal Derivative Models[J]. International Journal of Non-Linear Mechanics， 2016， 87（12）： 58-63.

[8] Mandelbrot B B. The Fractal Geometry of Nature[M]. New York： W. H. Freeman and Company， 1983.

[9] Ataei M， Kiyoumarsi A， Ghorbani B. Control of Chaos in Permanent Magnet Synchronous Motor by Using Optimal Lyapunov Exponents Placement[J]. Physics Letters A， 2010， 374（41）： 4226-4230.

[10] Heinz-Otto Peitgen， Hartmut Jürgens， Dietmar Saupe. Chaos and Fractals： New Frontiers of Science[M]. New York： Spr-inger， 2004.

[11] Heymans O， Fissett J， Vico P， et al. Is Fractal Geometry Useful in Medicine and Biomedical Sciences[J]. Medical Hypotheses， 2000， 54（3）： 360-366.

[12] Candela R， Mirelli G， Schifani R. PD Recognition by Means of Statistical and Fractal Parameters and a Neural Network[J]. IEEE Transactions on Dielectrics & Electrical Insulation， 2000， 7（1）： 87-94.

[13] Talebinejad M， Chan A D C， Miri A. Multiplicative Multi-fractal Modeling of Electromyography Signals for Discerning Neuropathic Conditions[J]. Journal of Electromy?ography & Kinesiology， 2010， 20（6）： 1244-1248.

[14] Y?lmaz D， Güler N F. Analysis of the Doppler Signals Using Largest Lyapunov Exponent and Correlation Dimension in Healthy and Stenosed Internal Carotid Artery Patients[J]. Digital Signal Processing， 2010， 20（2）： 401-409.

[15] Gaalaas L， Henn L， Gaillard P R， et al. Analysis of Tra-becular Bone Using Site-Specific Fractal Values Calculated from Cone Beam CT Images[J]. Oral Radiology， 2014， 30（2）： 179-185.

[16] Bagheri H， Ranjbari E， Amiri-Aref M， et al. Modified Fractal Iron Oxide Magnetic Nanostructure： A Novel and High Performance Platform for Redox Protein Immobilization， Direct Electrochemistry and Bioelectrocatalysis Applica?tion[J]. Biosensors & Bioelectronics， 2016， 85（11）： 814-821.

[17] Spasi? S. Surrogate Data Test for Nonlinearity of the Rat Cerebellar Electrocorticogram in the Model of Brain Injury[J]. Signal Processing， 2010， 90（12）： 3015–3025.

[18] 馮银波， 方向明， 陈宏伟， 等. 分形维数在CT腰椎松质骨图像中应用的研究[J]. 同济大学学报医学版， 2016（3）： 107-111.

[19] Bogaert C， Beckers F， Ramaekers D， et al. Analysis of Heart Rate Variability with Correlation Dimension Method in a Normal Population and in Heart Transplant Patients[J]. Autonomic Neuroscience Basic & Clinical， 2001， 90（2）： 142- 147.

[20] 刘晓芳， 叶志前， 刘群芳. 麻醉期心率变异性的分形特性分析[J]. 生物医学工程学杂志， 2006， 23（3）： 10-13.

[21] Mandelbrot B B， Wheeler J A. The fractal geometry of nature[M]. Birkh auser Verlag， 1991.

[22] 李潭. 基于分形理论的高速列车状态分析与故障诊断研究[D]. 成都： 西南交通大学， 2015.

[23] 王鹏程. 基于分形理论的结合面接触特性分析[D]. 昆明： 昆明理工大学， 2015.

[24] Harrouni S， Guessoum A. Using fractal dimension to quan-tify long-range persistence in global solar radiation[J]. Chaos Solitons & Fractals， 2009， 41（3）： 1520-1530.

[25] Sarkar N， Chaudhuri B B. An efficient differential box- counting approach to compute fractal dimension of image[J]. IEEE Transactions on Systems Man & Cybernetics， 1994， 24（1）： 115-120.