基于MATLAB的多种插值算法在地表时序监测中的应用研究

郭瑞 李素敏 陈娅男

摘  要： 为了克服InSAR技术获取数据时，由于部分月份缺失影像，而导致对研究区进行长时间序列形变分析时，所获取的形变序列为非等时距，不利于系统地反映其形变趋势的问题。本文基于MATLAB软件进行插值算法编写，对缺失时间跨度同的两种地表形变监测数据，分别进行多种插值算法实验。实验结果显示：对于缺失月份较少的数据，三次样条插值拟合效果最好;对缺失较多月份或分布不均匀的数据，立方插值拟合效果最好;线性插值和邻近点插值的拟合效果较差，不适用于对缺失的数据进行插值。该结果对由于缺失部分数据而影响其形变时序分析的情况提供了方法指导，具有较强的实用意义。

关键词： MATLAB，插值算法，数据缺失，形变分析

中图分类号： TP3    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2019.04.004

本文著录格式：郭瑞，李素敏，陈娅男. 基于MATLAB的多种插值算法在地表时序监测中的应用研究[J]. 软件，2019，40（4）：1824

【Abstract】： In order to overcome the InSAR technology acquisition data， due to the lack of images in some months， the long-term sequence deformation analysis of the study area， the obtained deformation sequence was non-equal time interval， which is not conducive to systematically reflect the deformation trend. In this paper， based on MATLAB software， the interpolation algorithm was written. For the two kinds of surface deformation monitoring data with the same time span， a variety of interpolation algorithm experiments were carried out. The experimental results showed that for the missing data， the cubic spline interpolation has the best effect. For the data with more months or uneven distribution， the cubic interpolation fits best; linear interpolation and adjacent point interpolation Poor effect， not suitable for interpolating missing data. This result provides a methodological guidance for the situation that affects the deformation timing analysis due to the missing part of the data，and has a strong practical significance.

【Key words】： MATLAB; Interpolation algorithm; Data loss; Deformation analysis

0  引言

相比傳统的地表形变监测技术，星载合成孔径雷达干涉测量（interferometric synthetic aperture radar，InSAR）以其高精度、高分辨率、全天候以及不受恶劣天气影响的优点在近些年迅速普及。但是由于其在获取卫星影像的过程中，会出现若干月份无影像或获取影像的时间间隔相差较大等问题，导致生成的地表时序形变图缺失部分月份数据，不便于分析。基于此，有必要利用合适的插值算法，对缺失的形变数据进行内插，获取其完整的地表时序形变图，进行地表形变分析。

李鹏、顾宏斌等利用三次样条法、双三次样条法的思路应用于气动导数查新，避免了以往线性插值的“局限性”，提高了计算结果精度[1]。杨力，钱博等利用三次样条插值方法处理BOC调制信号相关谱主峰及副峰数据，提高了相位测量精度[2]。吕建升等在采集离散点时加入编程算法，实现了生成等高线，并提高了成图精度[3]。聂磊、舒红等利用地理加权回归克里格插值，对地形地貌复杂、观测站点分布稀疏不均匀的地区进行了月尺度平均气温的插值方法及精度分析研究[4]。李雨、崔希民等基于Matlab运用曲线拟合法，采用模型编程求得矿区地表形变情况[5]。苏超威等利用Matlab软件并结合三次样条插值函数对地铁附近的地表形变做出了低相关监测及预报[6]。余礼仁、徐良骥等对缺失部分数据的地区，基于Matlab软件并利用三次样条插值算法实现了对缺失数据的补充，实现了对该区域的时序沉降分析研究[7]。

由于Matlab可以便捷高效地实现应用于此类问题中[8-12]，因此本文基于Matlab软件，分别采用Nearest、Linear、Spline、Pchip插值算法[13，14，15，16]对缺失部分数据的地表监测数据进行插值处理，获取完整的时序分析数据，并对四种插值算法精度进行比较。

1  不同内插反演函数的建立

1.1  线性插值（Linear）算法及实现

2  实验数据及处理流程

2.1  实验数据

实验中，采用2015年4月至2018年4月间获取的该地区60景Sentinel-1A数据并辅以SRTM 30m DEM数据，利用ENVI的SarScape模块对数据进行处理。

采集数据时间及获取的形变数据值如下表所示：表1数据获取的间隔时间较不均匀，虽只缺失2016-5-23到2016-10-14期间这一段数据，但缺失的数据时间跨度较大，接近5个月;表2数据获取的时间间隔较为均匀，缺失三段数据但缺失的数据时间跨度较小，均为36天，分别为2017-7-5到2017-8-10、2017-9-27到2017-11-2、2018-1-25到2018-3-2。由于部分的数据缺失，会影响后续对地表形变的时序分析，因此有必要采取插值算法对其进行插值处理。

2.2  数据预处理

由表1及表2可知获取的时间序列是基于日期排序的，不利于下一步的插值处理。若要进行后续处理，需要先对原始数据的横坐标进行转换，通过将获取数据的日期间隔转换为对应的x轴坐标间隔，然后通过依次累加获取其完整的x轴坐标。转换后结果见表3及表4。

2.3  插值算法应用

利用MTALAB软件，分别进行线性插值、邻近点插值、三次样条插值、立方插值算法的编写，对表1及表2进行插值计算。

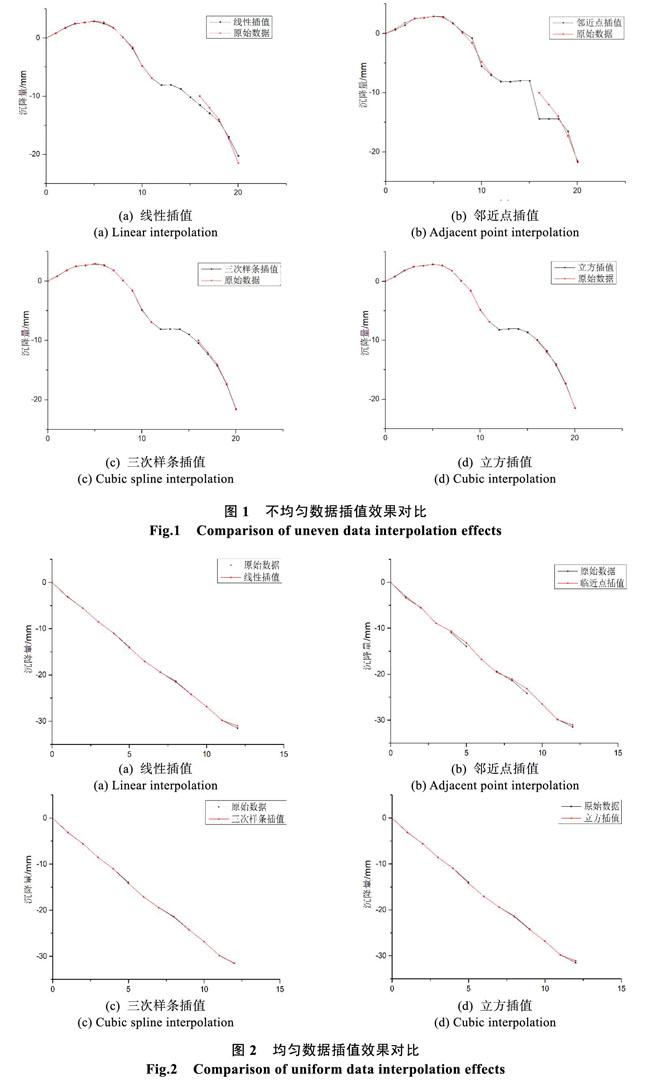
考虑到内插后的数据便于分析，采用1（即月为单位）为间隔对表1及表2数据进行插值，插值后的结果如图1所示。

度较好但是在插值后期的拟合度较差，插值出现明显跃变，不够平滑;邻近点插值拟合度较差，其插值跃变幅度大，引起的误差也相对较大，平滑度较差;三次样条插值与立方插值的拟合效果都比较好，这两种方法可以较好地表现出原始数据的走势，但立方插值的效果优于三次样条插值。对于均匀且缺失时间跨度较小的数据，线性插值、三次样条插值、立方插值都可以较好的拟合出原数据的趋势，拟合曲线光滑;邻近点插值法的拟合效果不好，拟合曲线平滑度差。

值方法速度较快，占用内存最小，但一般来说误差较大，并且插值结果不够滑，相比而言邻近点插值的平滑度更差;三次样条插值是所有插值方法中运行耗时最长的，插值函数及其一二阶导函数都连续，是较光滑的插值方法，占用内存比立方插值方法小，但是已知数据分布不均匀的时候可能出现异常结果;立方插值法中，插值函数及其一阶导数都是连续的，所以插值结果比较光滑，速度比三次样条插值快，但是占用内存最多。

综上，对于部分数据缺失的情況，一般应选用三次样条插值方式进行拟合，可以较快的拟合出较为真实的平滑值，但是在缺失数据较多，或数据分布不均匀的情况下，应选用立方插值拟合，可有效避免异常结果的出现。

3  不同算法地表形变结果分析

通过2.3中的插值算法应用，得出在缺失不同数据的情况下，应该采用何种插值算法。对表1中数据进行立方插值法插值，对表2中数据进行三次样条法插值。通过图3对比可以看处，未选择合适插值算法进行插值前的原始数据，因为缺少部分数据，无法对其进行时序沉降分析，但选择合适插值算法对原始数据进行插值后，获得了完整的时序沉降数据，便于对其分析。因此选择合适的差值算法，对于因缺失数据而影响其形变分析的地区，具有重要的实用价值。

4  结论

本文利用InSAR获取的地表时序沉降数据，融合四种插值算法，对缺失部分月份的数据进行插值拟合，结果发现：

（1）线性插值和邻近点插值误差较大，邻近点插值的拟合度最低。

（2）三次样条插值耗时最长但其平滑程度较好，对于缺失数据较少的情况，拟合效果较好。

（3）立方插值拟合结果较好，更适用于缺失数据较多或数据不均匀的情况，但其所占内存较多。

通过本文实验可以看出，对于缺失部分数据的原始数据在利用插值算法后，弥补了其因缺失数据而不能进行完整时序分析的缺陷，对进一步的地表形变监测分析具有重要的实用价值。

参考文献

[1] 李鹏， 顾宏斌， 高振兴. 三次样条插值法在气动导数计算中的应用[J]. 飞行力学， 2008（02）： 74-76+80.

[2] 杨力， 钱博， 冯永新， 薄煜明. 提高BOC调制信号多相关峰值精度的三次样条插值法[J]. 系统仿真学报， 2009， 21（12）： 3573-3576.

[3] 吕建升， 须鼎兴. 基于离散点绘制等高线算法的研究[J]. 现代测绘， 2006（05）： 5-7.

[4] 聂磊， 舒红， 刘艳. 复杂地形地区月平均气温（混合）地理加权回归克里格插值[J]. 武汉大学学报（信息科学版）， 2018（10）： 1553-1559.

[5] 李雨， 崔希民， 何荣， 李春意. 基于Matlab地表沉陷预测的自动实现[J]. 煤炭技术， 2018， 37（09）： 147-149.

[6] 苏超威， 丁克良， 周命端， 刘淼. 结合三次样条插值函数的地铁地表沉降监测预报模型[J]. 测绘通报， 2015（S1）： 160-162.

[7] 余礼仁， 徐良骥， 庞会， 王振兵. 融合三次样条插值的D-InSAR沉陷变形监测技术[J]. 测绘通报， 2017（09）： 51-55.

[8] 雒明世， 张倩琳.  基于MATLAB 的OFDM 系统仿真与教学研究[J].  软件， 2015， 36（6）： 152-157.

[9] 王赛男， 邢冬梅.  基于MATLAB 的小波阈值滤波与应用[J]. 软件， 2015， 36（10）： 102-104.

[10] 于洋， 袁健华， 钱江， 等.  新边界条件下的三次样条插值函数[J]. 软件， 2016， 37（02）： 25-28.

[11] 姜文涛， 刘荣海， 杨迎春， 等.  基于 MATLAB 时频分析算法的滚动轴承故障研究[J].  软件， 2018， 39（2）： 102-107.

[12] 孙彦超， 章坚民.  基于 MATLAB 的 DG 选址定容可视化系统的设计与实现[J].  软件， 2018， 39（4）： 142-147.

[13] 张梦远， 姚瑶. 吉林省气温与降水数据空间插值与分布研究[J]. 吉林农业， 2018（20）： 108-110.

[14] 王巍， 徐媛媛， 杨皓， 何雍春， 黄孟佳， 杨正琳， 袁军. 基于类线性插值算法的DDFS设计与实现[J]. 微电子学， 2018， 48（03）： 406-410.

[15] 陈爽， 张悦， 张勤俭， 曹宇男. 一种基于B样条插值的机器人速度规划算法[J]. 应用基础与工程科学学报， 2018， 26（03）： 661-671.

[16] 王玉春， 王昆， 阳海鹏， 欧阳群， 张其大. 几种插值和拟合算法在潮汐插值上的应用分析[J]. 科技创新导报， 2018， 15（08）： 114-115.