装配式斜交空心板桥受力分析及试验研究

杨晶晶 李睿 徐征

摘  要： 装配式斜交空心板桥受力比较复杂，在设计装配式斜交空心板桥时一般按正交桥来计算配筋，然而在竖向荷载作用下，其内力、应力、挠度都与相应的正交桥有明显的差别。本文通过对一座已建装配式斜交空心板桥分别进行单梁、整体梁格Midas civil模型计算，并与荷载试验结果相对比，得出了装配式斜交空心板桥的受力特点，指出了按正交桥来设计装配式斜交空心板桥在内力、应力、挠度等方面所存在的误差，为今后类似装配式斜交空心板桥的设计提供参考。

关键词： 装配式;斜交;空心板;横向分布计算

中图分类号： U442.5    文獻标识码： A    DOI：10.3969/j.issn.1003-6970.2019.04.017

本文著录格式：杨晶晶，李睿，徐征，等. 装配式斜交空心板桥受力分析及试验研究[J]. 软件，2019，40（4）：8487

【Abstract】： The prestressed hollow slab bridge is more complicated. When designing the prestressed hollow slab bridge， the orthogonal bridge is used to calculate the reinforcement. However， under the vertical load， the internal force， stress and deflection are corresponding. There are significant differences in orthogonal bridges. In this paper， a single-beam and integral beam Midas civil model is calculated for a prefabricated oblique hollow slab bridge， and compared with the load test results， the force characteristics of the assembled oblique slab bridge are obtained. The error of internal force， stress and deflection of the fabricated skewed hollow slab bridge is designed according to the orthogonal bridge， which provides a reference for the design of similarly fabricated oblique slab bridges in the future.

【Key words】： Assembled; Skewed; Hollow slab; Lateral distribution calculation

0  引言

在很多工程实际中，由于路线与所跨越的河流等存在障碍，而不得不采用斜交桥的方案[1]。斜交桥中，预制装配式空心板桥的应用相对较多。斜交桥的计算，往往近似地按正交桥来考虑，计算其横向分布系数，然后进行配筋[2]。而事实上，斜交桥梁的受力与正交桥有很大的区别，在同样的荷载作用下，其内力、应力、挠度的大小、分布等，都与正交桥有很大的区别，且这种区别会随着斜交角度的增加而增大[3，4];斜交板桥的锐角处与钝角处的受力相差较大[5]。本文以云南省某斜交空心板桥为例，对该桥在多种荷载工况下的受力特性进行计算分析并进行荷载试验。计算时，近似地按正交桥计算其空心板的横向分布系数，选取有代表性的单梁建立Midas civil单梁模型进行计算，并与Midas civil整体梁格模型、荷载试验结果进行比较分析，从而了解装配式斜交空心板桥的实际受力情况。

1  斜交空心板桥的受力特点

斜交桥的纵向主弯矩比跨径为斜跨长、宽度为b的正交桥小，并随斜交角的增大而减小如图1所示[6]，其次斜交桥的纵向最大弯矩的位置，随斜交角的增大从跨中向钝角部位移动如图2所示[7]。

预制装配式斜交空心板桥在垂直荷载下一般具有下列特性：1）在自重作用下最大挠度发生在跨中截面，且沿宽度方向均匀分布[8，9];2）装配式斜交空心板桥与整体式斜交空心板桥相比，在自重作用下的应力分布更加均匀[10，11];3）其剪应力的最大值集中在两个钝角的平分线上[12，13];4）自重小，整体挠度和结构的应力都相对较小[14，15];5）宽跨比对斜交空心板桥的影响：宽桥对斜支承敏感，窄桥斜支承只影响支承局部[16，17];6）装配式斜交空心板桥边板跨中弯矩最大值大于次边板和中板的跨中弯矩最大值[18，19]。

2  工程实例

2.1  工程概况

云南某斜交空心板桥，其上部结构为1-17米预应力混凝土斜交空心板，斜交角为45°。设计荷载城市A级;桥宽32米，横向由30块板组成，分左右幅，中板宽99 cm，边板宽99.5 cm，板与板之间的铰缝宽度为1 cm。钢绞线弹性模量取E= 195000 Mpa，标准抗拉强度1860 MPa，张拉控制应力按照图纸上所提供的数据，其值为0.72fpk=1339 MPa，对该桥进行荷载试验。

2.2  计算模型

综合考虑先张法预应力空心板的特点以及测试的需要，采用梁格法建立Midas civil模型，梁本身自重和预应力效应单独考虑。空心板材料为C50混凝土，其弹性模量、容重等材料参数均《公路桥涵设计规范》取定。弹性模量取E=34500 MPa，容重取γ=26 KN/m2，Midas civil全桥计算模型如图3所示。

2.3  试验荷载及加载方式

根据桥梁结构型式，确定了各加载截面的最不利内力，按照荷载等效原则，试验荷载拟由载重车辆车队组成。桥梁汽车试验荷载选用典型的三轴载重自卸汽车3辆，单车总重量400KN。其前轴承载80KN，两后轴分别承重160KN。试验车辆尺寸及轴重如图4所示。

2.4  工况的确定

本文的静载试验分为2个工况，其中以左幅为例。试验车辆纵向及平面布置如图5、图6所示，桥梁左幅应变测点布置如图7所示。

试验工况1：布置1、2号试验车辆加载;试验工况2：布置1、2、3号试验车辆加载。如图6所示。

2.5  橫向分布计算

为不失代表性，选取1号边板、9号中板、16号中板，近似地按正交桥的方法，分别用铰接板法和刚接梁法计算其横向分布系数，然后建立Midas civil单梁模型进行计算分析，并与Midas civil梁格模型、荷载试验的结果对比，最终得到装配式斜交空心板桥的实际受力状态。两种横向分布计算方法所得横向分布系数如表1所示。

3  受力特点分析

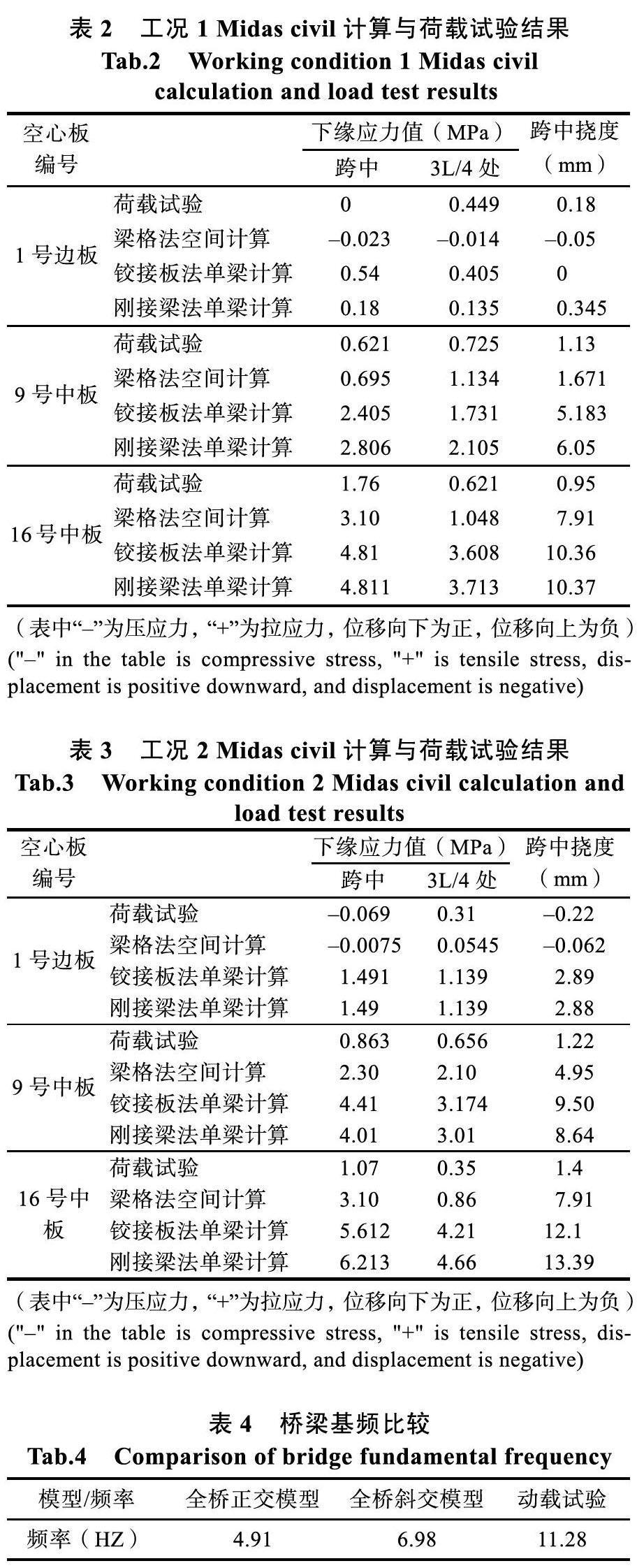
通过对比1号、9号、16号最不利纵板的两种Midas civil单梁模型、Midas civil梁格模型以及荷载试验的空心板板底应力值及位移，分析横向铰接板法、横向刚接梁法建立的模型应力及位移并与梁格模型计算结果、荷载试验结果比较，由此判断两种横向分布计算方法的误差大小。工况1、2条件下纵板1、9、16两类Midas civil单梁模型、Midas civil梁格模型及荷载试验的应力值及位移值如表2、表3。采用正交和斜交方法计算得到的基频与动载试验测试得到的基频如表4。

从表2和表3可以看出，发现Midas civil梁格模型计算结果与荷载试验数据最为接近，在荷载作用下，其实际应力、挠度，都比采用单梁模型计算的要小得多。从表4可以看出，采用斜交模型计算得到的桥梁基频比正交计算要大，且更接近实测值，也就是说，与同等跨径的正交桥相比，斜交桥的刚度相对较大。因此，在对斜交桥进行设计计算时，如果采用单梁模型，近似地按照正交桥的方法计算横向分布系数，再计算其内力、应力和变形，将得到相对保守的结果。同时，也会导致对桥梁受力特点的误判。

4  结论

通过对具有代表性的1、9、16号纵板进行分析，分别用Midas civil单梁模型和Midas civil梁格法模型进行计算，并与荷载试验对比，可以得到如下结论。

（1）斜交桥与正交桥受力相差极大，不应简单地采用正交桥的横向分布系数方法来计算斜交桥，否则，将会带来较大的误差;

（2）由于斜交桥特殊的受力特点，会使得其整体性比同等跨径的正交桥好，而且整体刚度比同等跨径的正交桥要大;

（3）对于斜交桥的设计和计算，必须采用有限元方法建模分析，才能得到相对准确的结果。

参考文献

[1] 王秀艳. 基于JTGD60-2004规范的斜板桥实用计算方法研究[D]. 上海： 同济大学， 2008： 5-6.

[2] 王良波. 装配式斜交空心板桥的受力特性及其承载力分析[D]. 长沙： 长沙理工大学， 2004： 12-13.

[3] 欧阳祥森. 装配式斜交空心板桥的受力特性分析与设计方法研究[D]. 长沙： 长沙理工大学. 2006： 15-16.

[4] 梁栋， 王云燕， 马金龙， 等. 装配式斜交空心板桥梁的内力简化计算方法[J]. 交通科技， 2015（6）： 1-4.

[5] 周爱国. 某斜交空心板梁桥荷载试验空间效应分析[J]. 中外公路， 2012（4）： 110-113.

[6] 杨彩霞， 柴金义. 有限元梁格法在斜交空心板计算中的合理性分析[J]. 内蒙古大学学报（自然科学版）， 2014（6）： 637-642.

[7] 刘小燕， 韦成龙， 欧阳祥森， 等. 装配式斜交空心板桥受力特性分析[J]. 公路工程， 2007（8）： 45-48.

[8] 屈计划， 唐国喜. 装配式斜交板桥空间内力分析方法[J]. 工程建设与设计， 2012（7）： 165-168.

[9] 郭晓涵， 芦娜. 基于SAP2000的通信三管塔风荷载加载方法研究[J]. 软件， 2016， 37（6）： 57-64.

[10] 张翅， 郑国梁. 结构化分析工具JS-SA中的关键技术[J]. 软件， 1996（1）： 6-8.

[11] 仝瑞金， 钟建国. 斜交装配式空心板桥受力性能影响分析[J]. 湖南交通科技， 2015（1）： 94-96.

[12] 袁友忠. 基于梁格法的斜交空心板桥计算分析[J]. 公路与汽运， 2016（5）： 167-170.

[13] 陈端迎. 面向建筑工程设计院所的生产项目管理平台研究与设计[J]. 软件， 2015， 36（10）： 108-110.

[14] 陈荣序. 斜交空心板桥受力特性的数值分析与实验研究[D]. 长春： 吉林大学， 2014： 5-6.

[15] 吴承坤， 阮永芬， 等. 软土地区基坑工程参数影响的敏感性分析[J]. 软件， 2018， 39（9）： 158-165.

[16] 王锴， 刘士全， 杨建. 单跨斜交桥受力分析[J]. 内蒙古公路与运输， 2012（6）： 27-29.

[17] 刘琳. 计算机软件工程管理与应用分析[J]. 软件， 2014， 35（2）： 141-143.

[18] Elgabbas. F， A A El-Ghandour， A A A bdelrahman， ASEL- Dieb. Different CFRP strengthening teehniques for prestressed hollow core concreteslabs：Experimental study and analytical investigation[J]. Composite structures. 2010， 92（2）： 401-411.

[19] Girhammar U A， M Pa jari. Tests and analysis on shear strength of composite slabs of hollowcore units and concrete topping[J]. Construction and Building Materials. 2008， 22（8）： 1708-1722.