基于混沌映射的散列函数加密算法分析及设计

向志华 赖小平

摘  要： 混沌序列具备散列函数所要求的单向性、扩散性、初值敏感性等非常多的特性，在混沌映射的基础上可以设计出优秀的散列函数来进行加密算法设计。密码学和混沌两者有着类似的结构和紧密的关系，这也使得混沌密码算法成为当代信息安全的重要研究内容。作为一种新的构造散列函数的方法，混沌映射正得到越来越多的关注。本文主要研究一种基于广义混沌映射的散列函数的加密算法，通过更改混沌方程的控制参数和状态值，更改混沌映射的方程获得不同的散列结果，可以更有效的防止攻击。

关键词： 散列函数;混沌;加密;算法

中图分类号： TP311.1    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2019.08.015

本文著录格式：向志华，赖小平. 基于混沌映射的散列函数加密算法分析及设计[J]. 软件，2019，40（8）：6669

【Abstract】： Chaotic sequences have many characteristics such as unidirectionality， diffusion and sensitivity of initial values required by hash functions. On the basis of chaotic mapping， excellent hash functions can be designed to design encryption algorithms. Cryptography and chaos have similar structure and close relationship， which makes chaotic cryptography algorithm become an important research content of contemporary information security. As a new method to construct hash function， chaotic mapping is attracting more and more attention. In this paper， a hash function encryption algorithm based on generalized chaotic map is studied. By changing the control parameters and state values of chaotic equation and changing the equation of chaotic map， different hash results can be obtained， which can prevent attacks more effectively.

【Key words】： Hash function; Chaos; Encryption; Algorithms

0  引言

传统加密算法和混沌系统两者的混合特性都比较好，并且它们的加密过程也相似。在传统加密算法中所具备的混乱特性，类似于混沌系统的类随机特性及参数敏感性。并且在传统密算法中所具备的扩散特性，这又类似于在混沌系统中的所具备的轨道混合特性，如轨道发散性和初值敏感性等。随着可信计算技术近年来的发展，散列算法的应用也越来越广泛。因此对混沌映射的散列函数的研究具有重要的实际意义。本文主要研究怎样将混沌思想应用到散列函数加密算法中。

1  散列函数介绍

在原有的单向散列方法中，主要存在有MD5，MD2，SHA-1等实现标准，要设计实现无碰撞的压缩函数，一般可以基于异或等逻辑运算的复杂方法来进行。基于异或运算本身所带有的缺点，就算被操作的文本长度很短，单步执行过程简化，计算的轮数也依然很大。基于安全的考虑，要求迭代的轮次必须足够多。

基于DES的分组加密说法可以通过多次迭代得到对应散列结果。在分组加密方法中，散列函数的执行效率和安全机制主要取决于所采用的基本密码算法，运算量较大，所以难以同时找到快速并可靠的加密算法。

2  混沌的概念

混沌，可以理解为：一种无序状态的集合，在确定的非线性系统中无需附加别的随机因素也会出现的随机行为[1]。混沌系统是由一种非线性函数f对其自身进行迭代所构成的[2]，即： 。在该系统中，根据上次迭代所得到的结果，再次使用相同的方法作二次及多次迭代。

在混沌系统中，有着复杂的动力学行为，和对初始状态和系统参数的异常敏感，因而很难用概率统计学原理进行重构并预测。同时，在混沌系统中，迭代过程是单向的，每次迭代都会生成截然不同的的结果。在一个混沌系统中，假设初值和系数是相同的，也将产生完全两个完全相同的迭代结果。

3  混沌映射与密码学二者的关系

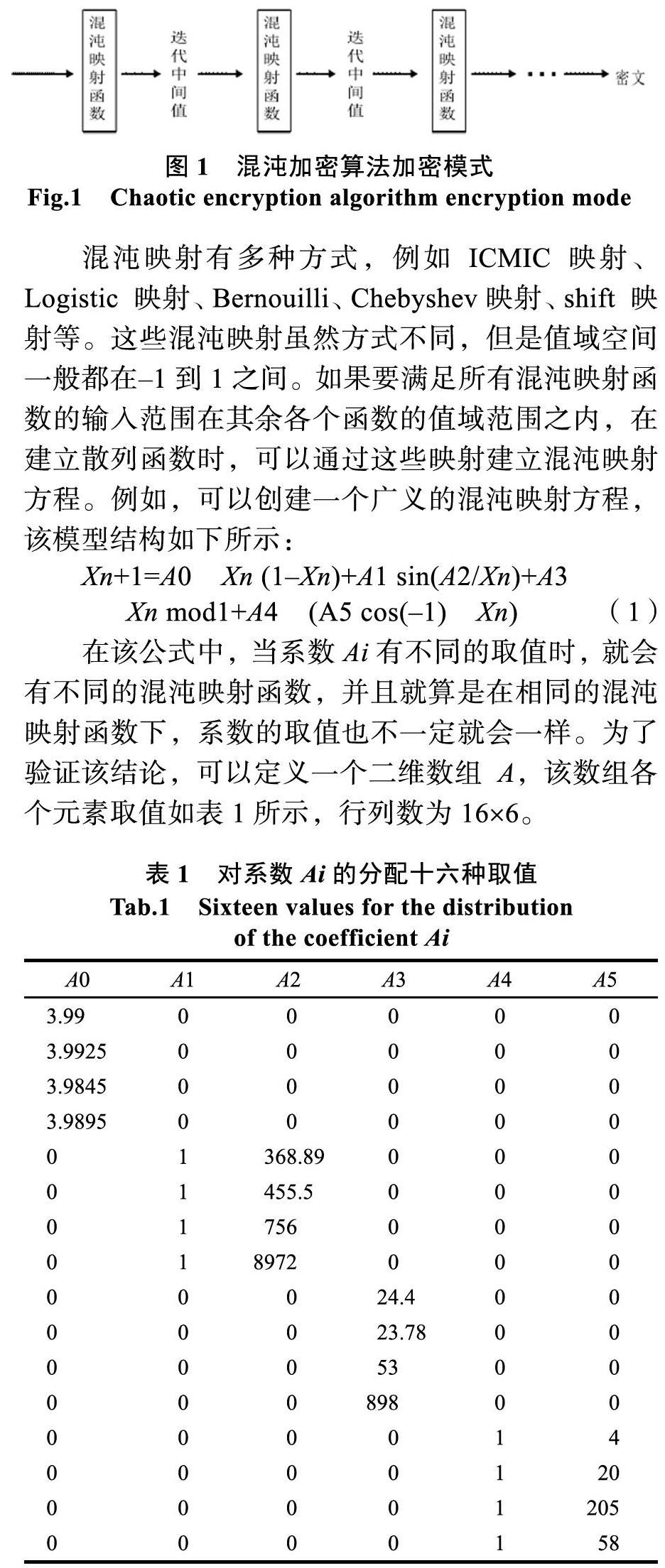
混沌系统有如下几个基本特性：有界性、确定性、对初始条件的敏感性、拓扑传递性和混合性、宽带性、快速衰减的自相关性、长期不可预测性和伪随机性[3]。在混沌系统中，由于它所具备的这些独特的基本特性，能让密码设计和保密通信得到更好的实现。建立确定的混沌动力学方程，也可以更好地保证通信双方可靠的进行信息收发及加解密。如图1所示的混沌加密算法加密模式：

密码算法与混沌映射的关系从操作过程和特性特点来看，两者是紧密相连的 。在操作过程上理解，在密码算法里面所用到的密钥相当于混沌的原始值。传统密码算法可以利用多轮加密方式，置乱密文和明文间的统计和推理关系，而混沌映射为了实现对对明文的扰乱也是通过多次迭代。从特性层面上理解，密码算法的混乱性类似于混沌的对原始值的敏感性，密码算法的扩散性类似于混沌的混合性。混沌軌道对初值十分敏感并且带有发散特点，刚好满足密码算法中所提出的扩散原则。密码算法中提出了混淆原则，而混沌吸引子也具备了混合特性与拓扑传递特点，还有对系统参数的敏感性。

用六种不同方式修改内容，并计算各自散列值，看看会有怎样的变化：

条件a：保持原文内容不变，初始参数h0=0.1，初始值X0=0.232323。

条件b：其余内容不变，把信息中的首字母“W”改成“X”。

条件c：其余内容不变，把信息中全部的单词ring改成rang。

条件d：其余内容不变，把信息末尾的句号改成逗号。

条件e：其余内容不变，在信息末尾添加一个空格符号。

条件f：其余内容不变，把初始值X0由0.232323设置为0.232325。

当修改条件后，产生的散列值用十六进制方式表示如下。

6  算法分析

（1）灵活性

虽然在散列函数中，通常为了得到长度确定的字符串，会将其它长度的字符串进行压缩操作。但是在不同的应用环境，散列值的长度也会有不同的要求，有些地方会将其固定为256比特，有些固定为128比特。在混沌映射的前提下，散列算法利用确定的方式，提取迭代值中的一部分比特位，再次重构后，获得最后的散列结果。散列值的位数可以根据实际需求很方便的改变，这与传统的散列算法相比有很大的优点，也具有更好的拓展性和灵活性。

（2）安全性

通过对算法改进后，可以得到16种不同的映射方式，所用到的密钥有两个：X0，其中0

7  总结

混沌映射是当前密码学领域的一个研究热点，它不仅具备散列算法所要求的各项性质，同时也兼备优良的密码学特点。虽然散列函数和混沌理论都各自有自己的优缺点，但是如果把两者的优点和特性结合起来，可以形成一种新的基于混沌映射的散列算法，不但可以提高加密算法安全性，还给攻击者破解密钥增大了难度。散列算法在文件校验、数字签名、远程认证方面有非常重要的作用，这些也是保证信息安全的重要途径。

参考文献

[1] 蒋君莉， 张雪峰. 基于多混沌系统的彩色图像加密方法[J]. 计算机应用研究， 2014（10）： 3131-3140.

[2] 薛香莲. 一种新的基于超混沌映射的彩色图像加密算法[J]. 计算机应用与软件， 2013（8）： 318-321.

[3] 认证加密算法专栏序言[J]. 胡磊. 密码学报. 2018（1）： 68-69.

[4] 方旋. 基于混沌映射的散列算法改进及其在密钥协商协议中的应用[D]. 武汉工程大学， 2013.

[5] 李达. 基于混沌映射的哈希函数分析与构造[D]. 北京邮电大学， 2011.

[6] 何婷婷 罗晓曙 廖志贤 韦正丛. 一种新的混沌映射散列函数构造方法及应用[D]. 物理学报， 2012.

[7] 刘长琦. 基于混沌序列的DES算法改进及实现[D]. 东北大学， 2009.

[8] 刘文兵. 一种FFTT非对称加解密算法的研究与实现[D]. 山东科技大学， 2011.

[9] 杨华千. 基于混沌理论的HASH函数研究现状综述[D]. 重庆工商大学学报（自然科学版）， 2012.

[10] 高路. 基于数字水印的三维CAD模型版权保护技术研究[D]. 浙江大学， 2010.

[11] 刘银森. 基于混沌加密的保密视频会议系统研究及实现[D]. 华南理工大学， 2011.

[12] 邱辰霖， 程礼. 一种基于相邻数据依赖性的混沌分析方法[J/OL]. 物理学报， 2016， 65（03）： 56-71.

[13] Zhang Y Q， Wang X Y. A symmetric image encryption algorithm based on mixed linear–nonlinear coupled map lattice[J]. Information Sciences， 2014， 273（8）： 329-351.

[14] 高瑞峰. 基于混沌理论和密文扩散的数字图像加密算法研究[D]. 安徽大学， 2017.

[15] 基于混沌系统的数字图像加密技术研究[D]. 侯文刚. 江西财经大学 2018.

[16] 基于混沌的数字图像加密算法的研究与设计[D]. 夏荣. 湖南大学 2018.

[17] 基于混沌系统的图像加密算法研究[D]. 吕群. 江南大学， 2018.

[18] Arnold置乱变换图像加密算法研究[D]. 方毅. 江西理工大学， 2018.

[19] 混沌圖像加密算法研究与实现[D]. 安守楠. 中北大学， 2018.

[20] 基于复合混沌的图像加密算法研究[D]. 吴贻峰. 兰州理工大学， 2018.

[21] 基于混沌理论与DNA编码的图像加密算法研究[D]. 胡裴龙. 安徽大学， 2018.

[22] 基于多混沌序列与隐写术的医学图像加密技术的研究[D]. 姜涛. 武汉科技大学， 2018.

[23] 张雪锋. 混沌序列生成技术及其若干应用研究[D]. 西安： 西安电子科技大学， 2011.

[24] Fridrich J， Kodovsky J. Rich models for steganalysis of digital images[J]. IEEE Transaction on Information Forensics and Security， 2012（3）： 868-882.

[25] Patidar V， Pa Reek N K， Purohit G. Modified substitution- diffusion ijnage cipher using chaotic standard and logistic maps[J]. Communications in Nonlinear Science and Numer?ical Simulation， 2010（10）： 2755-2765.