车辐式索桁架模态分析与试验研究

王泽强 刘占省 韩庆华 张维廉 周黎光

摘  要：通过跨度60m圆形车辐式索桁架屋盖1：10缩尺模型的模态分析和模型试验，考察了拉索预应力、矢跨比及内外环直径比3个变化参数对结构自振特性的影响，对比分析了前四阶振型的试验结果与理论计算结果。试验和分析结果发现：结构第一、二阶振型为反对称上下振动，第三阶为内环扭转振动，第四阶为内环相对扭转振动;两者频率误差在10%以内，试验振型与理论振型基本吻合;前四阶振型的频率均在10Hz以上，表明车辐式索桁架结构为低频动力响应，自振频率较小且分布密集;预应力水平越高，振型频率越大，则结构刚度越大;矢高增加，结构频率随之减小，结构更容易发生侧向失稳;内外环直径比越大，结构扭转刚度相对会减小，容易发生扭转失稳。

关键词：车辐式索桁架;模态分析;正弦激振法;试验研究;参数分析

中图分类号： TU 461     文献标识码： A   文章编号：

Abstract： Through the modal analysis and test of the 1：10 scale model of 60m circular spoke cable-trusses， the influence of 3 parameters of cable prestress， rise to span ratio and diameter ratio of inner and outer ring on the natural vibration characteristics of the structure were investigated. The results of test and theoretical of the first four order modal were compared and analyzed. It can be seen that： The first， second order vibration modes of the structure are antisymmetric upper and lower vibrations， the third order is the inner ring torsional vibration， and the fourth order is the relative torsional vibration of the inner ring. The frequency error is less than 10%， and the experimental mode of vibration is in agreement with the theoretical mode. The frequencies of the first four modes are all above 10Hz， indicating that the spoke cable truss structure is of low frequency dynamic response， and the natural frequency is small and the distribution is dense. When prestress level of the structure is higher， the modal frequency will increase， and the stiffness will also increase. With the increase of sagittal height， the structural frequency will decrease， and the structure is more prone to lateral instability. With the increase of the inner and outer ring diameter ratio， the torsion stiffness of structure will decrease and torsion instability will also occur.

Key words： spoke cable-truss structure;modal analysis;sinusoidal excitation method;test research;parameter analysis

車辐式索桁架是一种受力高效、结构轻盈的典型预应力钢结构体系，其主要由柔性的拉索和刚性的撑杆组成。在动力荷载的作用下，这种柔性结构可能会发生拉索松弛和拉索预应力损失现象;撑杆轴力方向的改变;甚至发生结构系统性共振等危害。在结构抗震、抗风、冲击荷载和爆炸荷载研究中，结构的动力响应不仅与外界的激励及其随时间的变化规律有关，更取决于结构自身的动力特性，即结构的振型和振动频率。因此，在结构的动力响应分析之前有必要对结构进行模态分析研究。

国内外对大跨空间结构的静力性能、模型试验研究较多，对车辐式索桁架结构的模态分析较少。蔺军[1]针对三种葵花型空间索系结构的模态对比分析，研究不同预应力水平对结构的自振特性影响和规律。郭彦林[2]针对宝安体育场进行缩尺模型试验，分别研究了主体索系结构和整体索膜结构的模态对比分析，研究表明膜材预应力对模态的影响不明显。孙文波[3]选取佛山世纪莲体育中心的车辐式索膜结构作为研究对象，着重分析不同预应力度和不同的膜的张拉刚度对结构自振特性的影响。结构的模态实验方面，李峰[4]针对凯威特—联方型弦支穹顶结构模型进行模态分析，探讨了外部荷载、矢跨比、环数比及支座形式变化参数对结构自振特性的影响。Yao Chen[5] 提出了一种高效的对称方法来确定多种独立自应力模式下各种索杆结构的整体预应力模态。对文章的独立单层外环梁，双层柔性拉索、小直径的内环的车辐式屋盖体系，结构的动力特性尚有待探究。

文章首先介绍了车辐式索桁架结构模态试验模型的设计方法，基于ANSYS 建立结构的有限元模型进行模态分析，通过试验测得结构的自振频率和相关振型，与理论结果对比分析，验证计算机模拟的可靠性。通过研究结构成型态初始预应力水平、矢跨比和内外环直径比对结构模态的影响和变化规律，为类似结构设计和动力性能评估提供参考。

1试验模型设计

1.1 相似比关系

试验以60米直径的某圆形轮辐式索桁架结构工程为背景，几何缩尺比例为1：10，应力比为1：1。长度和弹性模量的相似系数、为设计时首先确定的条件，针对本试验几何相似系数Sl=1/10，模型采用与原结构模型同样的材料，故材料相似系数Se =1/1。从而，模型与原结构模型中拉索、撑杆的截面积比为1：100。为了满足应力比1：1的要求，需要进行结构质量补偿，算出9倍的补偿自重荷载所产生的等效节点力，在节点施加质量块补偿荷载。文章主要考虑满足结构缩尺前后应力相等要求。柔性結构缩尺前后刚度的变化主要受位形和索力影响，质量块以节点荷载的形式作为质量补偿，试验结构的理论质量是减少的。所得的试验频率虽与原始模型有误差，但与试验理论模拟一致，验证了有限元模拟的可靠性。

根据结构模型进行计算分析、结构设计图纸前提下，选择了结构模型试验的各种杆件。其中，模型用的索材选用钢丝绳，弹性模量为1.3×105MPa，准确值由材料试验确定;钢管选用Q235B钢材。并结合市场供应情况，模型选用的材料和规格如表2所示：

1.2 结构模型与节点设计

结构模型直径为6m，由10榀鱼腹式索桁架、2道柔性环索和1道刚性受压环形工字梁组成。整体结构属于自平衡结构体系，即屋盖对主体结构只传递重力作用，无弯矩作用。屋盖结构下方有8根圆钢管柱支承，每根柱下通过4根地锚螺栓固定。模型三维图及立面图见图1～图3所示。

径向索与撑杆、环向索与撑杆等连接节点的形式与构造尽量与实际工程设计图纸为依据，最终确定出既可以用于模型试验，又具有可实施性的合理节点形式，并且遵循力学模型相似原则。具体节点设计见下图4～图6所示。

2有限元模态分析

模态分析所采用假定的计算模型，跨度为6m，矢高为200 mm，内环直径为1500 mm。本文利用ANSYS软件中APDL语言建立模型，撑杆杆件采用link8单元，弹性模量为2. 06 ×1011N/m2，屈服强度为235N/mm2;拉索采用link10单元，弹性模量为1. 3 ×1011N/m2，以施加初始应变的方法施加预应力;环梁采用beam188单元;活荷载为500N/m2。

有限元软件ANSYS中提供了多种相应的求解方法，主要有Subspace （子空间法）、Lanczos （分块兰克索斯法）、Reduced （凝聚法）、Unsymmetric （非对称法）、Damped （阻尼法）和QR Damping （QR阻尼法）。但是预应力钢结构而言，高阶振型参与比重变大，仅求解低阶阵型对整个结构的分析并不充足，高阶振型的求解非常有必要的。这就对结构特征值和特征向量的计算提出了更高的要求，需寻求更高效的大型稀疏对称矩阵广义特征值求解算法。因此借助ANSYS软件用Lanczos 法，对车辐式索桁架屋盖结构缩尺模型的模态进行分析，提取前6阶的阵型和频率，振型见图7所示，频率如表3所示。

从图7中可以看出前三十阶模态振型：第一、二阶为内环则呈反对称形式上下振动;第三阶为内环扭转振动;第四阶为内环相对扭转振动;第五、六阶均为索桁架呈对称上下振型，第七阶为内环上下振动;第八、九阶为索桁架水平面对称摆动振动;第十、十一阶为索桁架水平面反对称摆动;第十二阶至第二十一阶皆为索桁架水平方向摆动振动;第二十二阶至第三十阶皆为索桁架平面外扭转振动。

综上，振型特征可以概括为：低阶振型以竖向振型、水平竖向混合振型为主，高阶振型以水平振型为主;随着频率增加，水平振型开始出现，说明结构整体的竖向刚度要弱于水平侧向刚度，这是由于车辐式索桁架结构中各榀索桁架单元与外环梁铰接于一点连接，导致竖向刚度不足，提高预应力水平或设计成双层外环梁有利于提高结构的竖向刚度。从表 中可以看出，结构中心对称会导致多阶频率相等的情况发生;随着结构阵型阶数的增高，自振频率越来越大;结构自振频率密集，且前若干阶自振频率均偏低，该试验结构的基频在5Hz左右，说明结构的整体刚性较好。

3试验模态分析

3.1 试验设备

试验对象为车辐式索桁架屋盖结构的成型态，采用正弦激振法测量结构的动力特性。实验仪器有：DF1010超低频信号发生器，用以产生正弦波;KD5701功率放大器，将信号放大;电磁激振器固定于激振点处，与模型连接以施加正弦激振力;加速度传感器利用热熔胶水平或竖直粘结固定于节点上;使用动态信号采集仪器对结构加速度进行监测，包括16通道模块1个。实验仪器如图8所示。

由于采集通道数量的限制，加速度传感器布置在结构上层节点处，共布置16个加速度传感器。对称的第1榀和第6榀布置，其相邻榀和间隔榀分别布置，最大限度上保证加速度传感器的均匀布置。加速度测点布置如图9所示。

3.2 试验方案

将激振器的顶杆与结构通过钢丝和热熔胶固定好，以带动结构产生反复的振动。首先激振点选择第一榀内撑杆下节点，激振器沿内环索垂直方向竖向激振。将实验仪器安装调试好，加速度传感器竖向固定，以测得第一、二阶振型对应的频率。设置低通滤波器为10Hz，过滤掉高阶频率的干扰。手动调节信号发生器以改变不同的频率，此为扫频过程。观察各点加速度时程曲线，当在一定频率范围内各点加速度时程曲线的相位同时出现峰值，此时继续调节信号发生器的频率，振幅最大的加速度时程曲线对应的为第一阶振型，取其振动周期的倒数即为结构的第一阶自振频率。由于结构对称，将加速度传感器布置旋转90度，测得第二阶自振频率。按照此方法继续调节信号发生器，查找下一阶竖向振型对应的自振频率。

将加速度传感器水平向放置，选择一内撑杆下节点作为激振点，激振器水平激振，以同样的方法测得水平振型对应的频率。实验设备连接示意图见图10所示。

3.3 实验结果及分析

激出结构高阶频率需要激振器具有较大的激振力，才能使加速度时程曲线更明显，由于电磁激振器的限制，本实验只测得结构前四阶频率。对试验所得到的结构模型加速度时程曲线进行分析。第一次共振：加速度传感器竖向放置，信号发生器产生的正弦激励信号的频率为5.51Hz，加速度时程曲线振动周期为T1=0.184秒，则第一阶频率f1 = 5.412Hz;后续分析方法与之一致。试验模型自振频率试验值与理论值对比见表4所示。

可以得出，结构自振频率试验值整体偏小，误差原因可能在于：结构成型态拉索预应力并未达到设计值。 误差总体在10%以内，结果表明试验值与理论值吻合较好。

4參数分析

4.1 拉索预应力的影响

车辐式索桁架屋盖结构中预应力水平是指在拉索的预应力大小，是表征预应力钢结构的结构刚度重要指标。本文中将试验张拉的索定义为预应力水平的100%。在各构件预应力值的基础上，将结构的上径向索、下径向索、上环索和下环索的预应力值同时放大或缩小0.6倍、0.8倍、1.2倍和1.4倍，表5给出了结构成形态在不同预应力水平下，各主要构件的内力。陈志华[6]通过对天津保税区商务中心弦支穹顶结构的外环索预应力调整进行模态研究，表明结构预应力度对自振频率影响并不显著。孔文清[7]研究弦支网壳与单层网壳自振特性对比，振型与相应的单层网壳有本质的区别，但预应力大小对结构频率影响并不显著。这是因为弦支网壳刚度和质量的主要来源为上层刚性网壳。而对于全柔性的预应力索结构，孙文波[3]研究佛山世纪莲车辐式索桁架，发现预应力度与结构前几阶自振频率的关系基本呈线性变化，影响较大。蔺军[1]对葵花型索桁架研究发现预应力水平直接影响着结构的频率。这是因为全柔性结构的刚度完全由预应力提供。

图11给出了不同拉索预应力水平结构成型态下，前60阶振型的自振频率。首先，不同拉索预应力水平的结构，前几阶振型没有发生变化。但是随着预应力水平的增加，结构振型相对应的频率也在增加，如对应的基频分别为4.4402，5.1271，5.7322，6.2793，6.7823;由图可以看出，高阶频率比低阶频率变化显著，表明增加预应力水平，提高水平刚度比竖向刚度更明显。所以适当提高结构的预应力水平，提高了结构的抗变形能力。

4.2 矢高的影响

矢高指的是结构支座至结构最顶部的竖向距离。在预应力索网结构中，相同荷载的作用下，矢高的增加有利于提高结构的整体刚度，提高抵抗竖向位移的能力。沈世钊[8]针对椭圆形和菱形平面双曲抛物面鞍型索网结构，研究结果表明矢跨比对结构的低阶自振频率影响并不显著。高占远[9]通过研究劲性支撑索穹顶，得到矢高增加不利于结构扭转刚度的结论。

本结构为尽可能减少设计参数的改动，保持撑杆与下径向索角度不变，通过改变撑杆的长度，以达到改变结构矢高的目的。如图12所示，图中f表示矢高高度，△f表示矢高增量。根据《索结构技术规程》3.2.9规定，对于双层索系玻璃幕墙，索桁架矢高宜取结构跨度的1/10 ～ 1/20。该试验矢高采取150mm，200mm，300mm，400mm，500mm，600mm。内撑杆、中撑杆、外撑杆的高度原始比例保持一致1： 1.67： 1.99。

图14给出了不同矢高结构成型态下，前60阶振型的自振频率。首先，随着矢高增大，低阶自振频率略有减小，但并不是很显著;但是高阶自振频率减少比较明显，说明矢高的增加，结构水平刚度降低，对结构抗扭不利。

4.3 内外环直径比的影响

最早一批的双层车辐式索桁架结构是用于体育馆等封闭屋盖建筑，如：北京工人体育馆，四川广汉文体馆、布鲁塞尔世博会美国馆等等。此类体育馆特点为：1、内环为刚性结构，2、内环直径较小。近年来，大型的车辐式索桁架结构体育场中，内环不封盖、开口大，为柔性拉索。王昆[10]参考北京工人体育馆为算例，研究了柔性内环替代刚性内环的可行性，结构表明柔性内环的用钢量仅为刚性内环的33%。但缺点是实际工程中，柔性内环下料长度误差影响较大。

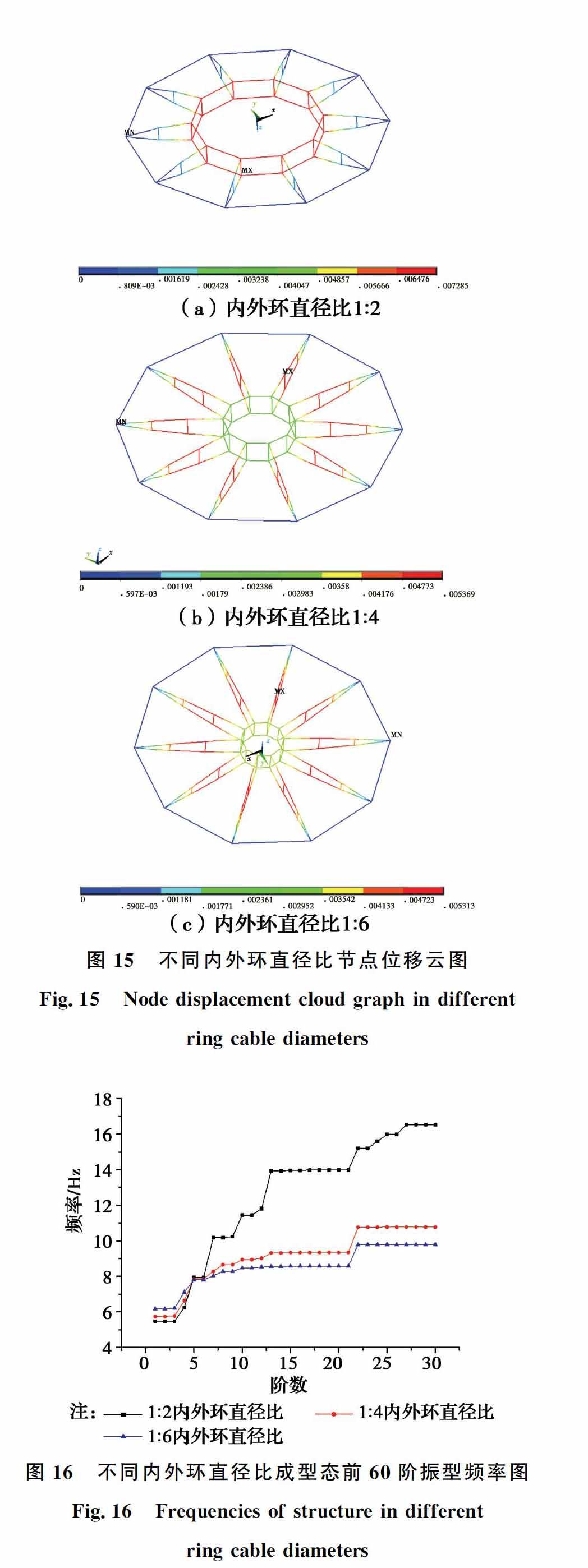
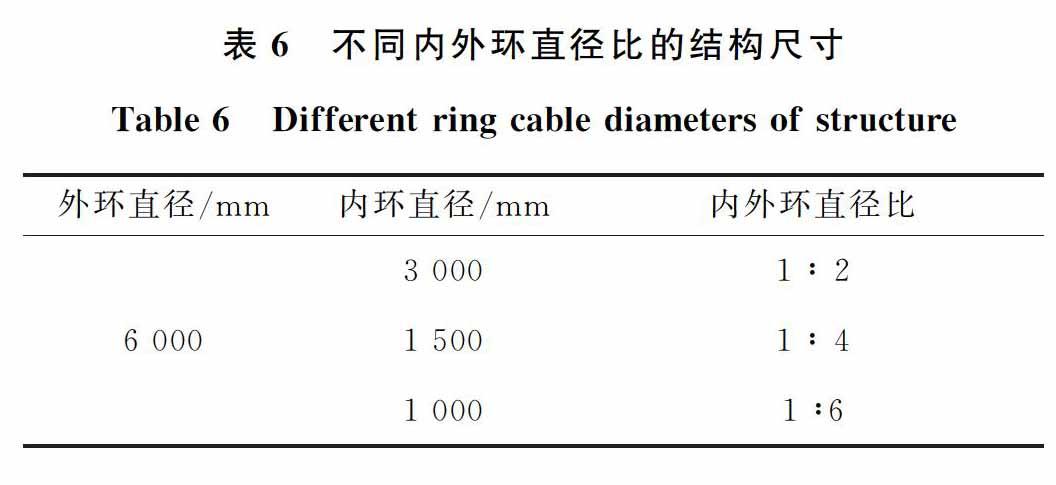
但是针对车辐式索桁架结构，柔性内环直径大小对其力学性能的影响和变化规律研究较少。根据《索结构技术规程》的规定，对于双层索系屋盖，当平面投影为圆形式，中心受拉与结构外环直径比宜取1/5至1/12。深圳宝安体育场、广州佛山世纪莲体育场内环与外环比约为1/2。在保持矢跨比、环向等分数不变的情况下，选取内外环直径比为1：2、1：4、1：6 三种工况。结构尺寸如表7所示。

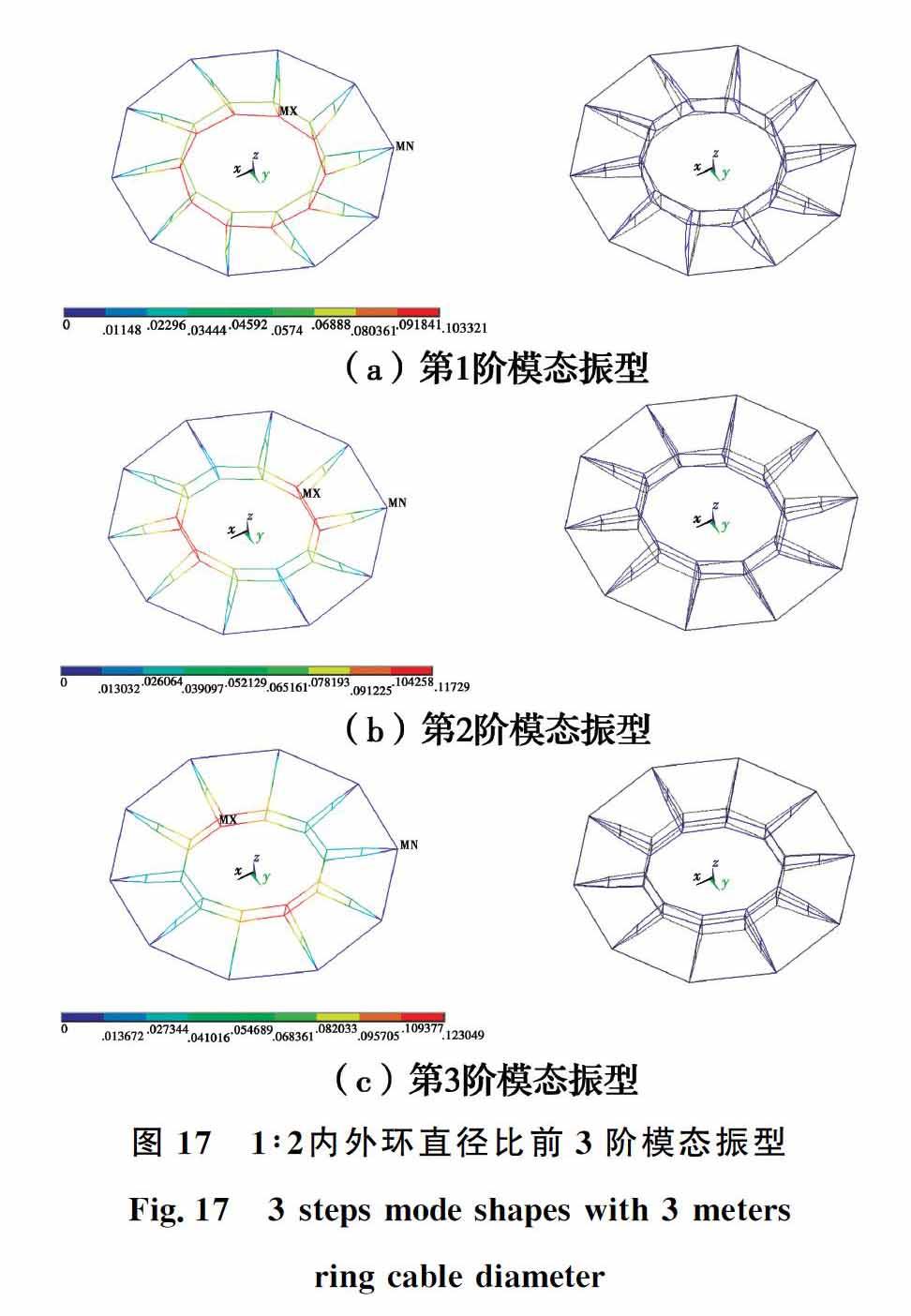
图16给出了不同内外环直径比结构成型态下，前60阶振型的自振频率。1/2内外环直径比的振型已发生变化。第一阶为内环扭转振动;第二、三阶为内环则呈反对称形式上下振动，与文献[2]一致说明了分析模型的准确性。如图17所示。

随着内环直径的减小，结构的第一阶振型由扭转振动变为竖向振动，表明内环直径大的扭转刚度弱于竖向刚度，内环直径的减小相对提高了结构的水平扭转刚度。高阶振型的以水平振型为主，高阶频率的增大也说明了上述结论的正确性。

5 结论

从理论分析和试验两方面研究了某圆形车辐式索桁架结构1∶10缩尺模型的模态特性，得到了成型态阶段的模态参数。利用ANSYS有限元软件进行建模计算分析;采用正弦激振法测试动力

特性，与理论值对比分析，明确了结构模型的自振特性;通过对预应力水平、矢高和内外环直径比等参数研究，为结构设计提供了相关参考。得到如下结论：

1）前四阶振型的频率均在10Hz以内，表明结构为低频动力响应。验证了车辐式索桁架结构自振频率较小且分布密集的结论。结构本身有多条对称轴，故有部分频率相等，振型大部分为正对称或反对称形状。

2）车辐式索桁架的结构刚度是由预应力提供的，结构预应力水平越大，结构的刚度越大，则振型频率越大。适当提高结构的预应力水平有利于结构整体的抗风性能和抗变形能力。

3）该结构频率随矢高增加而减小，高阶频率更为明显;内外环直径比对结构振型影响显著，内环直径增大，结构扭转刚度相对减弱。故在初步设计阶段，不能忽略矢高、内外环直径比对结构动力性能的影响。

参考文献：

[1] 蔺军， 冯庆兴， 董石麟， 等. 大跨度空间索桁张力结构的模型试验研究[J]. 建筑结构学报， 2006， 27（4）： 37-43.LIN J， FENG Q X， DONG S L， et al. An experimental study on large-span spatial cable-truss tensile structure model[J]. Journal of Building Structures， 2006， 27（4）： 37-43.（in Chinese）

[2] 郭彦林， 王昆， 孙文波， 等. 宝安体育场结构设计关键问题研究[J]. 建筑结构学报， 2013， 34（5）： 11-19.GUO Y L， WANG K， SUN W B， et al. Research on key structural design problems of the Bao'an Stadium[J]. Journal of Building Structures， 2013， 34（5）： 11-19.（in Chinese）

[3] 孙文波， 王剑文， 刘永桂， 等. 车辐式大跨度张拉索膜结构的自振和静风作用分析[J]. 工业建筑， 2007， 37（z1）： 672-675，690.SUN W B， WANG J W， LIU Y G， et al. Research on natural vibration frequency analysis and static wind loads for a rung-shape tensile cable-membrane structure[J]. Industrial Construction， 2007， 37（z1）： 672-675，690.（in Chinese）

[4] 李峰， 白友忠， 朱明. 凱威特-联方型弦支穹顶结构的模态分析[J]. 四川建筑科学研究， 2014， 40（4）： 41-44.LI F， BAI Y Z， ZHU M. Modal analysis of Kiewitt-Lamella suspen-dome structure[J]. Sichuan Building Science， 2014， 40（4）： 41-44.（in Chinese）

[5] CHEN Y， FENG J， MA R J， et al. Efficient symmetry method for calculating integral prestress modes of statically indeterminate cable-strut structures[J]. Journal of Structural Engineering， 2015， 141（10）： 04014240.

[6] 陈志华，郭云，李阳.弦支穹顶结构预应力及动力性能理论与实验研究[J]. 建筑结构， 2004， 34（5）：：42-45.

CHEN Z H， GUO Y， LI Y. Experimental research and analysis of the prestress and dynamic behavior for suspendom structure system[J]. Building Structure， 2004， 34（5）： 42-45.（in Chinese）

[7] 刘婷婷. 弦支穹顶结构自振特性及动力性能分析研究[D]. 济南： 山东建筑大学， 2013.LIU T T. The analysis on vibration characteristics and dynamic performance of the suspen-dome structure[D]. Jinan： Shandong Jianzhu University， 2013.（in Chinese）

[8] 薛素铎， 何永发， 李雄彦， 等. 劲性支撑穹顶结构模态特性参数分析[J]. 世界地震工程， 2015， 31（1）： 1-7.XUE S D， HE Y F， LI X Y， et al. Modal characterristics parameter analysis of rigid bracing dome[J]. World Earthquake Engineering， 2015， 31（1）： 1-7.（in Chinese）

[9] 郭彦林， 田广宇. 索结构体系、设计原理与施工控制[M]. 北京： 科学出版社， 2014. [英文书名]：

GUO Y L，TIAN G Y.Cable structure system， design principle and construction control. [M].Beijing：Science Press，2014：178-185（in Chinese）.

[10] 冼耀强， 刘伯权， 丁江澍. 世纪莲体育中心动力特性及反应谱分析[J]. 建筑科学与工程学报， 2011， 28（3）： 106-112.XIAN Y Q， LIU B Q， DING J S. Dynamic characteristics of century lotus stadium and response spectrum analysis[J]. Journal of Architecture and Civil Engineering， 2011， 28（3）： 106-112.（in Chinese）

（编辑：邓云）