法布里-珀罗（F-P）干涉仪测量钠灯波长差中的实验调节优化技术

黄昊翀，江佳鑫，丁 琪，熊树龙，张天权，高 华，董爱国，刘 昊，肖 畅，郑志远

（1. 中国地质大学（北京）数理学院，北京 100083；2. 中国地质大学（北京）工程技术学院，北京 100083）

1 “法布里-珀罗（F-P）干涉仪情景介绍

法布里-珀罗干涉仪（以下简称F-P干涉仪）是一种结构简单，光谱分辨率高的多光束干涉光学度量仪器，其应用范围广阔，被作为核心组件在温度场、风场等重要测量领域发挥关键性的作用。学习F-P干涉仪及光学干涉仪的基本原理和操作对高等院校理工科学生的科学素养培养、实验动手能力提升以及物理思维启发都有着积极的正面作用，是大学物理实验课程的经典教学实验之一。F-P干涉仪测量钠灯波长差”实验能充分利用该干涉仪高光谱分辨率的特点，通过光学干涉手段解析钠光灯微小的波长差值，一方面使学生充分了解F-P干涉仪的原理和结构；另一方面学习了干涉仪的操作流程及应用知识，启发学生将光学知识和自己相关专业结合提出更多的应用实例，做到学以致用[1-12]。

F-P干涉仪的实验内容主要过程包括原理讲解，干涉仪干涉条纹调节和测量及计算光源波长差。实验中有以下3个方面的原因会导致实验操作时间较长：

（1）在F-P干涉仪干涉图样调节中，需将两片玻璃板调至严格平行状态，调节过程对于第一次接触干涉仪的学生操作者有一定困难，一般情况下需要长时间调节才能获得较清晰的干涉圆环以便后续测量；

（2）通过光源标准波长差值反推计算可知，微调鼓轮在测量过程中需转动约30圈，单次测量即会消耗较长的时间；

（3）由于需进行逐差法计算数据，保证消除测量误差，同一物理量需多次数据测量。

原因（2）中的单次测量本身耗时较长，在此基础上多次测量操作时间会出现成倍增长，因此在测量和结果误差计算的过程中，学生因个体实验技巧差异会出现完成整个实验操作时间较长的现象。此外，F-P干涉仪作为光学实验，需人眼长时间直视观察光源和干涉圆环，在实际教学过程中，长时间记录和观察操作的学生通常会出现视觉疲劳的状态，降低了实验结果记录的准确性，也对接触实验的学生心理带来一定的压力和影响。因此，在保证实验测量准确性和精度的前提下，如何缩短实验操作时间，减缓操作者视觉疲劳，提高实验效率，让首次接触光学干涉仪实验的学生在有限的时间内能充分掌握仪器的操作流程，成为实际教学之中的重点。

本文对“F-P干涉仪测量钠灯波长差实验”提出了放大法调节干涉条纹并给出详细的调节步骤，以及提出基于粗调鼓轮与微调鼓轮混合调节的有效改进方案，之后对改进方法和原传统操作方式分别测量实验数据结果，证明所提方法在保证测量准确性的前提下可有效缩短实验操作时间，同时探索和解决新方法产生的鼓轮补零问题。最后分别采用原方法和改进方法对钠光灯进行测量，通过数据计算得到由实验测出的波长差，并与标准值进行对比分析误差，得出最终结论。

2 F-P干涉仪原理

F-P干涉仪的基本原理可简单总结为内表度有高反射率膜的平行玻璃板通过调节间距测波长差。其核心部件是2片相向面镀有高反射率膜的平行玻璃板，包括两者之间的空气层一起组成了F-P腔。通过仪器上的微调鼓轮和粗调鼓轮旋钮，可精确调节空气膜的厚度，即2片玻璃板之间间隙的宽度，由此改变干涉圆环的图像形貌。

F-P干涉仪测量光源波长差实验过程中，首先需将2片玻璃板调整至平行状态。干涉仪的基本原理如图1所示，其中p1和p2分别表示2片玻璃板，d代表 2片玻璃板间距，即空气薄膜厚度，s代表入射光线，φ为光束在镀膜表面上的倾斜角，数字分别代表了透射光和反射光。根据多束光干涉原理，钠光灯光线入射经过第一片玻璃板后到达空气层，之后在第二片玻璃板高反射率膜表面形成反射光和透射光，其中反射光在2片玻璃板的高反射率膜间来回反射，之后继续形成反射光和透射光。而由于2片玻璃板呈现平行状态，透射光部分为平行光，依次从第二片玻璃板后透射射出。透射平行光在无穷远处形成干涉，为了便于观察，通常使用透镜或望远镜器件对射出光线完成汇聚。

图1 F-P干涉仪多光束干涉的基本原理图

传统的钠光灯波长差测量过程中，实验者通过旋转粗调鼓轮调节2片玻璃板之间的距离，使干涉图样的大小和形貌达到最佳观测条件。之后通过旋转微调鼓轮增加或减小2片玻璃板之间的间距改变光程差，同时观察干涉条纹变化。由于钠光灯的两个波长等效于2个独立的单色光源，在干涉面上会各自形成独立的干涉圆环，当干涉圆环上某一位置的干涉光程发生变化时，根据等倾干涉的原理，干涉圆环整体会出现向外冒出或向里缩进的现象。而两波长干涉形成的圆环由于波长值不同，向外冒出或向里缩进的速度会出现差异，从而周期性呈现如图2所示的变化。图中2组圆环分别代表波长较长的光线和波长较短的光线形成的干涉图样，假设初始状态2套干涉圆环处于重叠状态，在2片玻璃板之间光程改变的过程中，干涉图样依次会出现2组圆环镶嵌双环状态，均匀圆环状态，2组圆环反向镶嵌双环状态，最终回到2组圆环重合状态。整个变化定义为一个周期，在一个周期内短波长形成的干涉圆环会比长波长多移动一个级次。

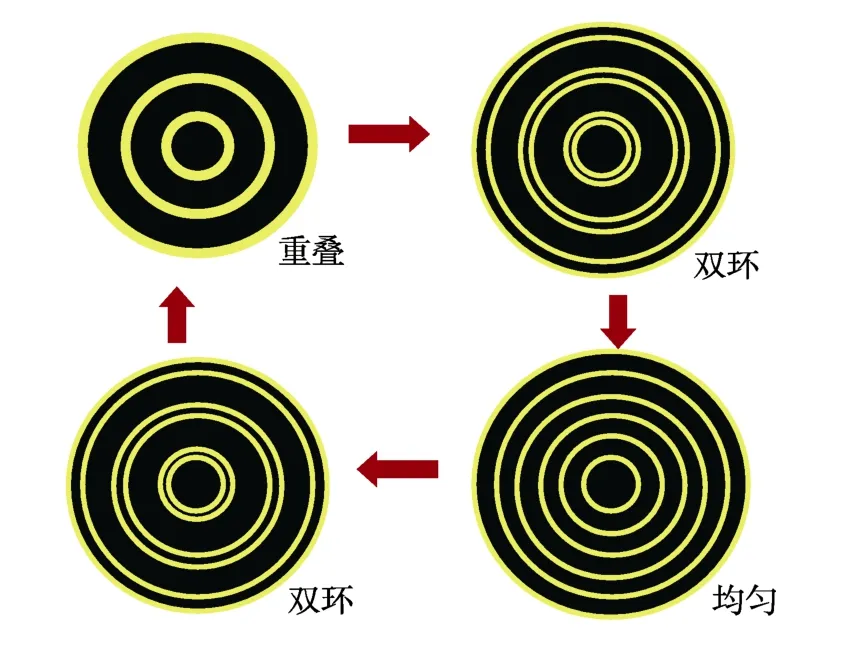
图22组干涉圆环随光程改变的变化规律

3 改进方案原理及流程

3.1 逐步放大法调节干涉条纹的流程

干涉条纹的调节是该实验的重点和难点之一，由于调节难度较大、要求较高，学生在具体操作时往往会消耗较多时间去完成该项目的操作，现有实验教学中的调节原理和目标叙述较为概括，即将2片玻璃板调至完全平行的状态。为指导学生更好更快地完成干涉条纹调节，将F-P干涉仪条纹调节的步骤整理分为5步，在这一过程中加入放大透镜和望远镜，调节过程以2次对光源图像的逐步放大为分界，具体步骤如下：

（1）调节内容为旋转两块玻璃板背后的黑色俯仰角螺丝以改变玻璃板角度，调节目标为从外部观察到镜片互相平行，之后继续调节使观测区内钠黄光灯的重影重合消除。当2片玻璃板接近平行状态时，钠黄光灯的多次反射透射像会处于同一位置，即重影通过重合方式消除，同时可以观测到光源图像上出现指纹状图形。

（2）完成第一次放大。在钠黄光灯和F-P干涉仪之间放入一块凸透镜，凸透镜的作用为对光源图像的放大。在放大过程中根据透镜成像原理，需注意保持透镜与钠黄光灯之间的距离，调节目标为让钠黄光灯的黄光放大至尽量充满观测区。通过透镜放大，玻璃板之间的微小倾角被同时放大，学生可以更好地通过观测干涉条纹了解玻璃板的平行度。

（3）通过观测区内观察干涉条纹，会出现光强分布不均匀干涉圆环。此时调节内容为继续慢速调节黑色俯仰角螺丝，调节速度和范围需比上一步更小，调节目标为在观测区内看到圆环圆心，同时调节圆环和光强分布的中心重合，达到尽量圆、尽量清晰的状态。

（4）完成第二次放大。加入望远镜观察条纹，望远镜的作用除汇聚平行光使之干涉之外，也起到放大的作用。

（5）调节内容为微速调节黑色俯仰角螺丝，调节速度和范围需比上一步更小，调节目标为在望远镜内观察到清晰度好、对比度高的干涉圆环。当观测到清晰度较差、较模糊的图像时，也可改用微调精度螺丝调节，使图像达到清晰度高的状态。

按照上述步骤操作，可以有效帮助学生完成干涉圆环的调节，相比直接进行调节要节省时间和降低难度。

3.2 双鼓轮混合调节法的原理与操作流程

传统调节方法利用微调鼓轮精确改变空气层厚度，测量条纹变化一个周期所改变的光程差，从而计算光源的波长差。在实验操作过程中，根据已知数据可知，实验人员每一个周期需旋转大约数10圈的微调鼓轮，同时长时间观察干涉圆环的变化情况，本文中所提改进方法主要聚焦于微调鼓轮操作上所展开的研究。

针对该问题，提出双鼓轮混合调节测量法来缩短测量时间，减少该实验的视觉疲劳误差。改进方法的原理主要基于仪器上粗调鼓轮与微调鼓轮的关系，微调鼓轮旋转一圈会带动粗调鼓轮行走一小格刻度，可通过粗调鼓轮直接调节数值去代替微调鼓轮的一圈转动，基于此原理的粗调鼓轮与微调鼓轮混合调节法由此提出。该方法替代传统的微调鼓轮测量方法能有效缩减操作时间和观察时长，也就相应缓解了实验人员的视觉疲劳。但在测量过程中需特别注意微调鼓轮的“补零”过程，才能使整个测量过程准确地获得条纹周期变化的光程改变量。

粗调鼓轮与微调鼓轮混合调节法的具体流程如下：

（1）微调鼓轮操作。完成2片玻璃板的平行调节之后，需将微调鼓轮和粗调鼓轮完成初始调零，消除零点误差。之后通过旋转微调鼓轮，寻找某个便于观察的干涉条纹形貌为起始图形，之后旋转微调鼓轮同时观察干涉圆环冒出或缩进现象，记录起始位置读数。假设首个周期操作者无法提前探知一个干涉条纹变化周期中2片玻璃板之间光程差的改变量，可采用传统旋转微调鼓轮方法测量。通过首次测量和理论计算可知，微调鼓轮需转动约30圈可以完整观察到干涉条纹出现如图2所示的一个周期的变化。

（2）粗调鼓轮操作。由上一步测量数据可知，可用粗调鼓轮直接旋转20小格刻度即2大格刻度，来替代微调鼓轮前20圈的转动，达到同样的玻璃板移动距离。在第二组数据测量时，可首先使用粗调鼓轮替代微调鼓轮调节旋转，粗调鼓轮的转动方向需和微调鼓轮转动方向一致，以消除系统的空程误差。

（3）微调鼓轮操作。在完成粗调鼓轮的调节之后，继续通过微调鼓轮旋转同时观察条纹变化情况，进行干涉图样整个周期的测量。同样，该次微调鼓轮调节时，转动方向应与粗调鼓轮方向相同。

（4）“补零”操作。由于微调鼓轮旋转时可以带动粗调鼓轮旋转，但粗调鼓轮直接旋转时微调鼓轮并不会同时改变刻度，因此采用两鼓轮混合调节法时，需特别注意“补零”问题，即任意时间调节旋转粗调鼓轮的前后，需保证微调鼓轮刻度处于零值位置。在实际测量中，完成微调鼓轮测量一个周期之后，如微调鼓轮的刻度线不在零点位置上，应将微调鼓轮调节至零刻度位置，同时记录该段距离改变量，计算在下一周期的距离总值之内。只有完成补零操作之后，才可以继续旋转粗调鼓轮计数，确保消除测量误差。

以此类推，之后每一周期的调节，均采用上述顺序流程，即微调鼓轮先调零，后调粗调鼓轮旋转，最后微调鼓轮旋转，并记录所得数据。因此在本文表格中，为表现该方法的过程记录了3组数据，分别为微调鼓轮补零操作，粗调鼓轮调节操作，以及微调鼓轮旋转值，干涉条纹变化一个周期2片玻璃板之间距离的改变量为三者之和。

4 实验数据对比与分析

为了验证所提方法测量的可行性，分别对传统微调鼓轮调节法和混合调节法分别完成实验记录，比较两者在测量准确性上的异同。2组实验调整到干涉条纹双环重叠状态开始实验，同时均通过调零法消除零点误差之后记录数据。

4.1 传统测量法实验结果

为对比测量效果，首先采用传统方法记录实验数据，即直接通过微调鼓轮改变两块玻璃板之间的光程差值。分别由甲乙两位不同操作者完成2组数据的记录，通过列表法记录测量的数据，数据值共测量6组。实验中可通过主刻度尺、粗调鼓轮和微调鼓轮的读数直接记录到位移玻璃板的位置刻度值d，同时表格中记录了微调鼓轮大约转动经过的整数圈数，记录得到的2组数据如表格1所示。

表1 传统记录方法得到的实验数据

从表格1的数据可知，在测量过程中，干涉条纹每出现一个周期变化，大约需要转动微调鼓轮约 30圈，即对应改变实际距离大约0.3 mm。传统记录方法表明，微调鼓轮在转动过程中，实际带动了粗调鼓轮转动了超过20小格（即2大格），即粗调鼓轮刻度改变远大于0.2 mm，由此可知两鼓轮混合调节法方案从理论上讲可行。

4.2 双鼓轮混合测量法实验结果

采用双鼓轮混合调节法的实验同样由上述实验相同的甲乙2位操作者完成2组数据的记录，数据记录过程中，记录的微调鼓轮“补零”操作转动的距离刻度小格数值对计算结果并无影响，只是为了更形象表达记录过程。之后记录粗调鼓轮旋转的刻度格数，在本实验中该值均为2大格，对应实际距离值0.2 mm。最后记录微调鼓轮旋转的圈数，即旋转微调鼓轮直到观察到干涉条纹回到初始状态。测量实验数据如表格 2所示，表格中的微调鼓轮补零刻度值、粗调鼓轮转动刻度值和微调鼓轮旋转整圈数三栏记录内容主要作用为还原和描述双鼓轮混合调节法的操作流程，在实际实验中只需和传统微调鼓轮记录法相同，记录下最终刻度读数即可。

4.3 数据处理与分析

完成实验数据记录之后，本文分别对传统方法测量的数据和双鼓轮混合调节法数据分别完成处理和分析，计算被测钠光灯的波长差值。首先为减少随机误差影响，通过逐差法计算6组数据中平均间距Δd，由于钠光灯的两个波长λ1和λ2差值较小，两者相乘可近似为钠光灯平均波长平方，则钠光灯的波长差 Δλ可表示为：

其中，钠光灯的平均波长值为589.3 nm，已知钠光灯波长差标准值为0.597 nm，可计算得到的光源波长差和标准值之间的误差α。

通过传统调节法测量得到的数据经数据处理之后，可得两组平均光程差值分别为Δd1=0.29869 mm和 Δd2=0.29837 mm，计算得到的波长差值分别为Δλ1=0.58133 nm和Δλ2=0.58195 nm，两者通过计算得到误差值分别为α1=2.6%和α2=2.5%。通过分析以上数据可知，2组测量结果和标准值之间的误差均未超过5%。

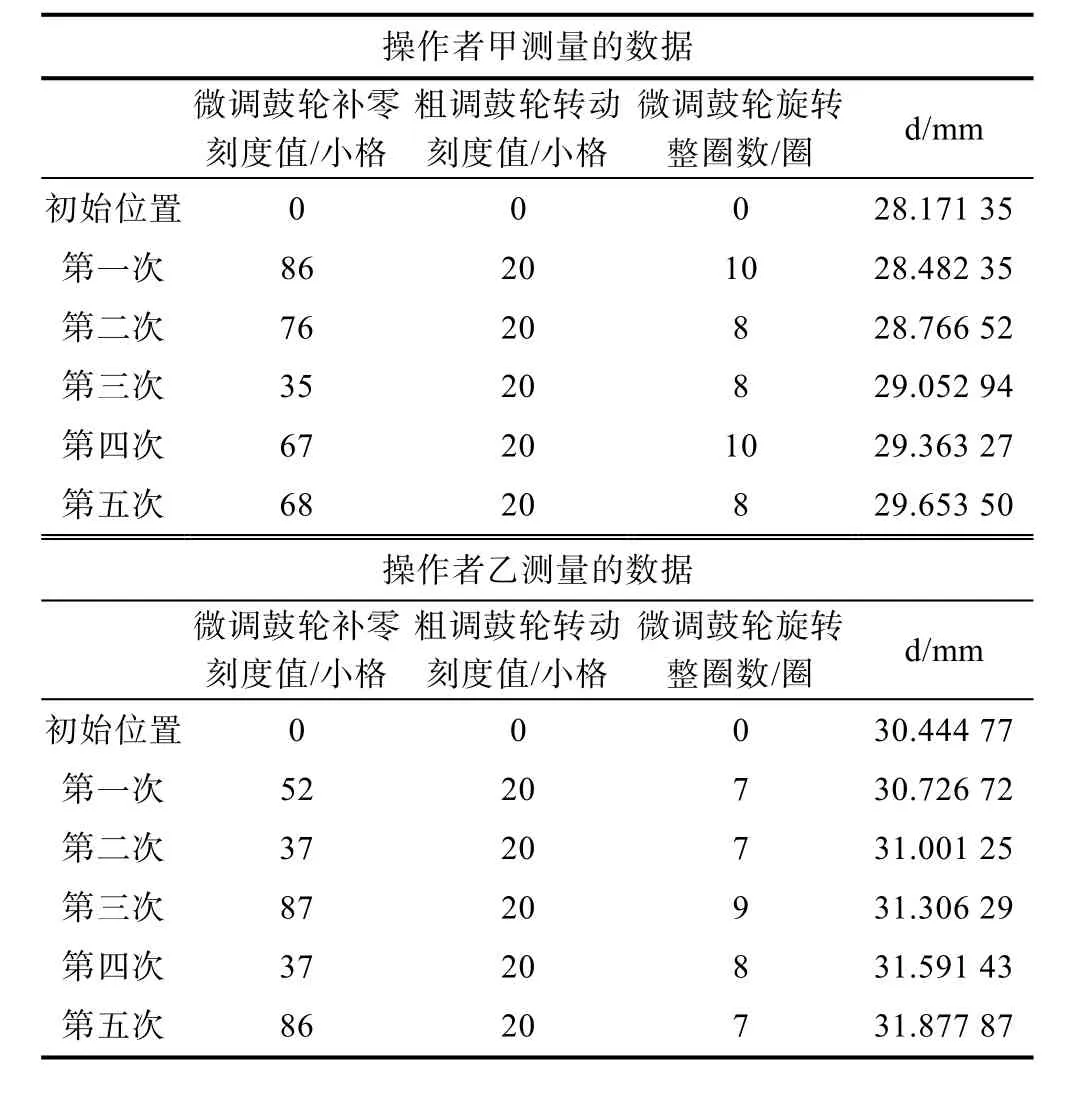
表2 双鼓轮混合调节法得到的实验数据

之后对两鼓轮混合调节操作法记录的2组数据完成计算，计算得到每个条纹周期光程变化值分别为Δd3=0.29439 mm和Δd4=0.28921 mm，之后计算得到波长差分别为Δλ3=0.58982 nm和Δλ4=0.60038 nm，通过改进方法计算得到的波长差和标准值之间的误差分别为α3=1.2%和α4=0.6%。

运用 Matlab软件分别对传统调节方式第一组结果和双鼓轮混合调节方式第一组结果做线性拟合分析，可得到结果分别如图 3(a)和图 3(b)所示。图中紫色圆点代表所测数据值，横坐标为测量组数，纵坐标为位置值d，红色实线代表线性拟合曲线，红色虚线代表预测界。通过数据分析可知，图 3(a)中的线性拟合曲线的R值为0.9999，均方根误差结果为0.0060，图3(b)中线性拟合曲线的R值为0.9998，均方根误差结果为0.0080。结合图形曲线分析可知，所提方法所测数据的线性度和传统方法基本一致，线性拟合曲线和数据差值微小，可认为测量结果符合真实线性变化情况，从另一个侧面也验证所提双鼓轮混合调节法的可行性和准确性。

通过数据结果对比得到的光源波长差值，改进方法在误差率上几乎相同甚至优于传统方法，同时有效地缩短了实验的操作和观察时间，缓解了操作者因长时间观察图形的视觉疲劳问题，在提高操作效率的同时也减小了因视觉疲劳而产生的测量误差。

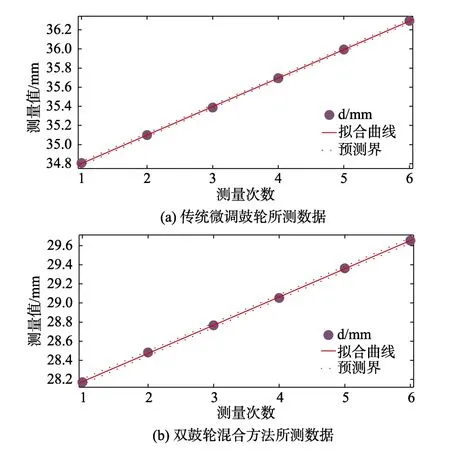
图3 实验数据的线性拟合曲线

5 结语

本文首先对F-P干涉仪测量钠灯波长差的实验内容中干涉仪的成像和测量原理进行简单介绍，尤其针对干涉圆环调节过程和测量过程中长时间旋转微调鼓轮旋钮及观察干涉条纹变化规律而导致的视觉疲劳和误差问题开展讨论和研究，给出了干涉圆环的逐步放大调节方法的详细步骤和双鼓轮混合调节改进方法来替换传统的微调鼓轮调节方法。之后，为对比所提方法操作的可行性和测量的准确性，分别由2位实验人员采用传统测量方法和改进测量方法，使用同一仪器对同一光源的波长差完成测量。通过计算对比分析得出的同一操作者完成实验的数据结果，两种方法的测量结果均在误差范围之内。所提干涉圆环调节方法和双鼓轮混合测量方法能有效缩短实验所需时间，缓解操作者的视觉疲劳，进而提高数据测量的精确度，从理论分析和实际操作上均有很强的可行性。在实际教学过程中，放大干涉条纹调节方法可作为基础实验教学内容，而双鼓轮混合调节方法则可以作为提升实验教学内容，这2种方法能够激发学生的创新思路及学习兴趣，加深学生对该实验的理解，可得到更好的教学效果。