一种基于改进最大最小蚁群算法的虚拟机放置策略∗

刘晋西

（武汉数字工程研究所 武汉 430074）

1 引言

云计算［1］是一种新型的商业模式和服务模式，这种模式提供了用户所需的一切，作为一种服务，它满足在任意时间、任意地点交付使用。作为云计算的服务最终提供者，数据中心［2］有着非常复杂的计算设备和存储设备以及大型的电力系统等。随着云计算的飞速发展，数据中心的规模也与日俱增。有研究表明，在数据中心的所有开销中，有70%来自服务器的采购开销以及配电和冷却的基础设施开销，剩下的30%则是提供服务导致的电力开销和网络开销［3］。我们所能做的就是优化这后30%的电力开销和网络开销。

有研究表明，优化数据中心的资源管理，能够有效地提高资源的利用率，降低电力开销和网络开销［4～6］。图1为数据中心的资源管理图。

2 问题描述

在进行虚拟机的初始化放置时，满足客户的需求以及最小化电能消耗和网络资源消耗是要兼顾的。也就是说，需要在满足客户需求的同时也要尽可能使得数据中心的电能开销和网络开销达到最小值。

这里需要考虑下面的因素:

电能开销。研究表明，数据中心的电能开销主要来源于服务器的电能开销，而服务器的电能开销又与CPU、内存等有着不可分割关系，其中CPU占据着绝大部分［7～8］。研究发现，物理节点的电能消耗和CPU利用率呈正相关。即当CPU由完全空闲的状态到满载的状态时，CPU利用率相应的由0上升到100%，物理节点的电能消耗也随之呈现上升的趋势。有些学者发现，当物理节点完全空闲时，它的电能消耗是满载时的70%［9］。这一结论充分说明适当的关闭空闲的物理节点有助于降低数据中心的电能消耗。可以用下面的公式来计算物理节点的电能消耗:

这里Poweri代表的是物理节点i的电能消耗，Bi为这台物理节点上已经被使用的CPU资源，Pi为这台物理节点上未被使用的CPU资源。这样一来就有两种方法可以降低服务器的电能消耗。一是减少开启服务器的数量，二是开启消耗电能较少的服务器。所以在虚拟机初始化放置时，应尽可能地将虚拟机集中放置在消耗电能较小的服务器上。

这里data（i，j）是一个 n×n 的方阵，代表所有虚拟机之间的通信频率，n为虚拟机的数量。cost为是一个k×k的方阵，代表物理机之间的通信开销，k为物理机的数量。π（i）则代表虚拟机i放置在物理机的编号。

至此虚拟机的初始化放置问题转化为多目标的优化问题。我们的目标是在满足虚拟机资源请求的前提下，将虚拟机放置在合适的服务器上，使得整个的电能开销和网络开销达到最小。即使得下面的公式在满足约束条件的前提下成立:

其约束条件如下:

1）任意一台物理机上的所有虚拟机对CPU资源的请求的数量之和不能超过物理机本身的CPU资源数量，即

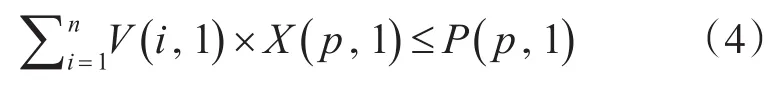
2）任意一台物理机上的所有虚拟机对存储资源的请求的数量之和不能超过物理机本身的存储资源数量:

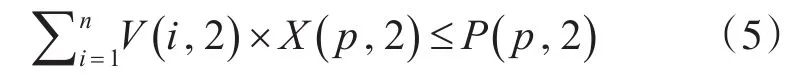
3）任意一台物理机上的所有虚拟机对带宽资源的请求的数量之和不能超过物理机本身的带宽资源数量:

4）同一时刻一台虚拟机只能位于一台物理机上:

宏观周期的本质是围绕长期趋势线波动的债务周期，利率则可以加快或推迟宏观周期的运行。油价既是宏观周期的一部分，被动受到宏观周期的影响，同时油价的自身波动又会影响利率和货币政策，进而影响宏观周期。

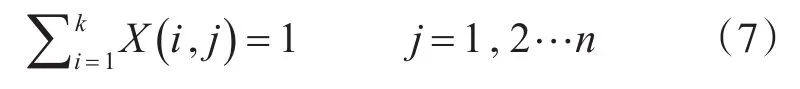
在上述的约束条件中，V是一个n×3的矩阵，第i行的每一列分别代表虚拟机i的CPU资源请求数量、存储资源请求数量和带宽资源请求数量。P是一个k×3的矩阵，第k行的每一列代表物理机k的CPU资源总数量、存储资源总数量和带宽资源总数量。

3 算法实现

相比于传统的蚁群算法［13～14］，最大最小蚁群算法［15］设置了信息算的浓度区间，也就是说最大最小蚁群算法中信息素浓度不能无限制地增大或减小，这样一来不仅使得求解速度大大加快，而且也可以防止算法过早地停滞。

3.1 信息素的更新

几乎所有的蚁群算法中，信息素τij的更新都会遵循这样的规则:

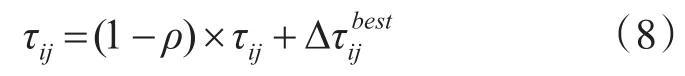
这里ρ为挥发因子。

在改进的最大最小蚁群算法中Δτibjest的表达式如下:

这里的Cbest就是式（9）的最小值，参数b的选择可以视情况而定，最终使得信息素浓度的增加不至于过快的达到上限或者下限从而导致蚂蚁无法做出选择。

3.2 概率转移函数

每只蚂蚁会被随机的放置在物理机上，然后根据一个概率转移函数从可以被放置在该物理机的虚拟机中选择一台虚拟机并放置。为了避免已经被放置的虚拟机再次被放置，会有一个数据禁忌表用来存储已经放置的虚拟机和不能被放置在该物理机的虚拟机。直到本次循环结束，清空禁忌表，蚂蚁才能再次自由选择。以下是概率选择函数的表达式:

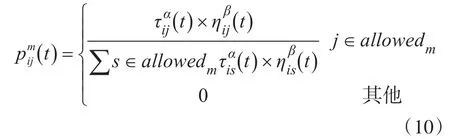
上式中allowedm表示蚂蚁m下一次允许选择的虚拟机，也就是禁忌表中剔除的部分，τij(t)为t时刻的信息素浓度，ηij(t)为t时刻的能见度，α和β分别为信息素启发式因子和能见度启发式因子。

3.3 最优解的构建

具体构建最优解的时候，在算法的每次循环中，蚂蚁根据概率转移函数在所有等待被放置的虚拟机中选择，每只蚂蚁在完成一次循环后会得到一个局部最优解。此时将这个局部最优解暂时保存为全局最优解，若下一只蚂蚁的局部最优解优于全局最优解，则将全局最优解更新；否则保留全局最优解。在所有的蚂蚁完成循环后就可以得到全局最优解。

算法流程如下:

第一步，初始化。初始化虚拟机请求的资源、物理机的资源、蚂蚁的数量、信息素挥发因子、信息素的上下限以及循环次数；

第二步，将一只蚂蚁任意放在一台物理机i上；

第三步，蚂蚁根据转移概率矩阵对禁忌表以外的虚拟机进行搜索，搜索到合适的虚拟机就将其放在物理机i上，将已放置的虚拟机数量加1并且更新禁忌表；

第四步，判断物理机是否可以放置更多的虚拟机，如果是，则转向第三步，如果否，转向第五步；

第五步，蚂蚁转向下一台物理机并判断虚拟机是否放置完毕，如果是，转向第六步，如果否，转向第三步；

第六步，根据公式（9）计算C，清空禁忌表并判断这个C是否小于Cbest，如果是，转向第七步，如果否，则忽略这个C；

第七步，将第六步的C赋值给Cbest，记录当前的虚拟机放置方案，蚂蚁数量加1，并判断蚂蚁数量是否到达上限。如果是，转向第八步，如果否，转向第二步；

第八步，循环数量加1，并判断是否到达循环次数的上限，如果是，则算法结束，Cbest为最优解，相应的虚拟机放置方案则为最佳的方案，如果否，则转向第二步。

4 实验与分析

数据中心的总体开销，包括电能开销和网络开销，也就是式（9）的结果是我们在本文最关心的。因此选择了最大最小蚁群算法和本文中的算法加以比较，即将两种算法的总体开销作为比较的对象。

由于模拟与实际有一定的差距，因此选择不同规模的数据集来进行50次模拟，并对最后的结果取平均值，以此来减小误差。

不同规模的数据集如下:

表1 物理机和虚拟机资源配置表

表2 机器数量

算法性能的评估指标定义为

由图2可以看出，相比于最大最小蚁群算法，改进的最大最小蚁群算法在系统的总体开销中有大约5%的性能提升。这是因为在这个算法中，一方面我们总是选择将虚拟机集中放置在消耗电能较小的服务器上，另一方面我们总是将通信频率高的虚拟机放置在通信开销小的服务器上。既减少了电能开销又减少了网络开销。因此改进的最大最小蚁群算法在总体开销上才会有性能的提升。

图2 性能提升度（百分比）

5 结语

本文将一种改进的最大最小蚁群算法应用于虚拟机的初始化放置问题中，在保证服务质量的前提下，可以使得整个系统的电能开销和网络开销达到最小。实验结果表明，相比于最大最小蚁群算法，改进的最大最小蚁群算法在系统的总体开销中大约有5%的性能提升。