基于遗传算法的汽车主动悬架LQR控制研究∗

许 伟高 远

（1.四川工商职业技术学院 成都 611830）（2.广西汽车零部件与整车技术重点实验室 柳州 545006）

1 引言

汽车作为现代的重要交通运输工具之一，在人们的日常生活工作中占有着举足轻重的地位。悬架作为汽车的重要组成部件，承担着把路面激励作用于车轮的各种力及其产生的力矩传递到车架，吸收和缓和因路面激励引起的振动［1］。目前，大多汽车还是采用参数固定不可调、价格相对便宜的被动悬架系统，难以满足人们日益增长的新需求，因此能够根据实际路况和汽车状态适时调节悬架刚度或阻尼从而获得较高的舒适性、平顺性及安全性能的汽车主动悬架系统将会在汽车上得到广泛推广应用。

控制策略是汽车主动悬架系统获得最优性能的关键［2］，针对汽车主动悬架控制策略问题，国内外学者们也提出来很多的控制策略，比如模糊PID控制［3～5］、神经网络控制［6～7］、鲁棒控制［8］及最优控制［9～10］等。其中最优控制理论成熟，实际控制效果较好，往往得到设计者的青睐，如何设计最优控制的加权系数是控制器获得最优性能的关键问题，但其加权系数并没有确切的解析方法，往往依赖设计者主观经验试凑决定加权系数，这样的“最优”控制设计效率低下而且也难以获得最佳性能。文章以二自由度汽车非线性主动悬架作为研究对象，悬架模型近似线性后，设计LQR控制器，其中利用遗传算法的全局搜索优化能力设计LQR控制器的加权系数，既提高悬架控制器设计效率，也保证了最优控制性能，仿真结果也验证了遗传算法优化LQR控制器的加权系数是有效的。

2 汽车主动悬架动力学模型

文章选取二自由度汽车非线性主动悬架系统作为研究对象，其动力学模型如图1所示。由牛顿第二定律，可得动力学微分方程［11］:

式中:m1为悬架的簧上质量；m2为悬架的簧下质量；k1为悬架刚度；k2为轮胎刚度；c为悬架阻尼；z1为车身垂向振动位移；z2为轮胎位移；q为路面不平度输入；ε为反映非线性影响程度的参数；u为主动控制力。

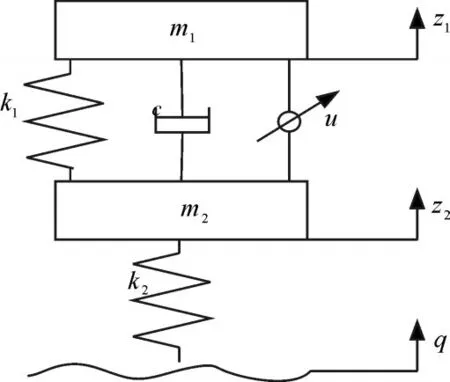
图1 二自由度汽车非线性主动悬架模型

3 基于遗传算法的汽车主动悬架LQR控制器设计

3.1 悬架模型近似线性化

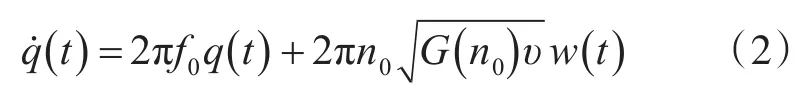
式中:q(t)为路面位移，单位m；f0为下限截止参考频率，通常取为路面不平度系数，单位为m3；w()t为零均值的高斯白噪声。则近似线性化后的悬架模型的空间表示式如下:

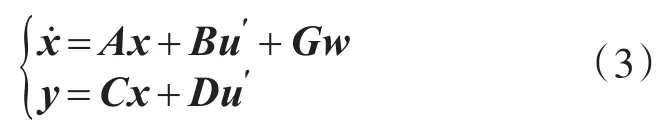
式中:

3.2 汽车悬架的LQR最优控制器设计

为进一步改善主动悬架的乘坐舒适性、操纵稳定性和行驶安全性，即要求所设计的LQR最优控制器应尽可能降低车身垂直加速度、悬架动挠度和轮胎形变，此外还需考虑控制能耗，使控制能耗较小［14］。因此，LQR控制器设计选取车身垂直振动加速度z¨1、悬架动挠度 z1-z2、轮胎形变z2-q和控制作用力u′构造如下线性二次型最优控制目标函数

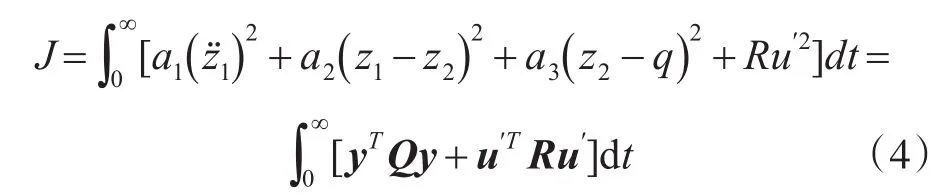
式中:a1、a2、a3和R分别代表车身垂直振动加速度、悬架动挠度和主动控制作用力在LQR控制中的重要性加权系数；和为加权系数矩阵。

式（4）可进一步整理为

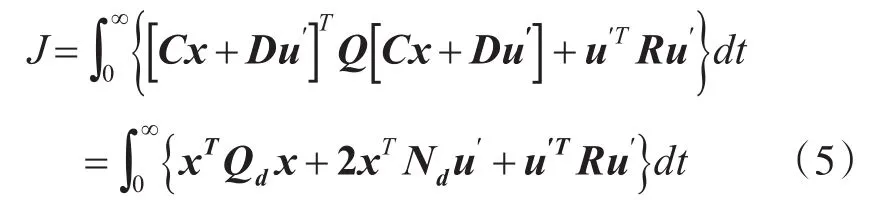
结合式（3），则有

根据线性二次型最优控制理论，可知LQR控制器的最优控制力为

式中:K为反馈增益矩阵。在考虑线性二次型最优控制目标函数趋于稳态时，Riccati方程的解L为常数矩阵，可以如下Riccati方程求出:

可求解出Riccati方程的解，并得到反馈增益矩阵K，从而结合式（6）中最优控制力，可设计出主动悬架的最优控制器。

可以看出，加权系数a1、a2和a3直接决定了LQR控制器的性能好坏。在具体设计中，因加权系数并没有确切的求解方法，控制效果只能依赖设计者主观经验试凑加权系数，这样的“最优”控制设计效率低下，而且也无法获得最佳性能。因此，文章利用遗传算法的全局搜索能力，研究引入遗传算法对LQR控制器的加权系数a1、a2和a3进行全局搜索优化设计，解决人为经验试凑导致的最优控制的非“最优”问题。

3.3 基于遗传算法优化设计加权系数

采用遗传算法全局搜索LQR控制器加权系数a1、a2和 a3的流程的步骤如下［15］:

1）遗传算法在如式（10）所示的设定范围内随机产生加权系数的初始种群。其中初始种群个体值使用实数编码，表达形式为。

2）将随机产生的初始种群的个体值分别赋值给LQR控制器的加权系数a1、a2和a3，由式（8）中的Matlab函数指令求解出最优控制器的反馈增益矩阵K，再将反馈增益矩阵 K代入式（6），获取LQR控制器的最优控制力，将最优控制力代入悬架系统模型中，运行仿真获得悬架的性能指标。

3）将上一步骤获得的悬架性能指标代入式（9），获得种群中各个体的适应度函数的具体数值，以满足约束条件式（11）下适应度函数极小值为程序终止条件。如果满足，退出程序并返回种群中最优个体x值；若不满足，转至下一步骤。

4）通过进行遗传算法的选择、保优、交叉和变异等操作，产生种群的新种群x，转至步骤2）。

4 仿真结果与分析

以某型汽车悬架为例，其系统参数:m1=371.5kg，m2=45.4kg，k1=22000N/m，k2=192000N/m，c=1500N·s/m，ε=0.4，仿真中考虑汽车以车速v=20m/s行驶在C等级路面（G0=2.56×10-4m3）上。运行遗传优化程序，优化所得到的加权系数的最优个体及其适应度函数变化情况如图2所示。

图2 最优个体及其适应度函数变化情况

由图2可知，随着种群的不断进化，最优个体的适应度函数逐渐收敛到2.8047，此时所对应的最优个体为，将加权系数 a1、a2和 a3其带入加权系数矩阵Qd、Nd、Rd中，可得到反馈增益矩阵:

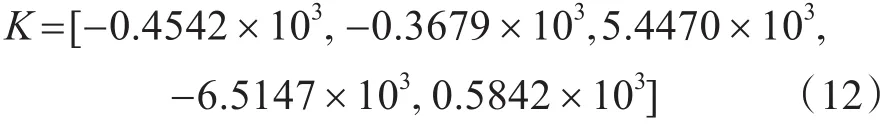
基于Matlab/Simulink环境，搭建如式（1）的非线性悬架系统模型，引入式（2）的随机路面输入激励，将式（13）的最优控制力代入非线性悬架模型中。仿真中考虑汽车以车速v=20m/s行驶在C等级路面的行驶工况，如图3～5分别是实施基于遗传权值优化LQR控制和无控制的被动悬架在上述工况下的车身垂直振动加速度、悬架动挠度和轮胎形变的响应曲线。表1是实施基于遗传权值优化LQR控制和无控制的被动悬架在上述工况下各性能指标均方根值。由图3～5和表1可见，相比于无控制的被动悬架，实施了基于遗传算法权值优化LQR控制的汽车主动悬架，在相同路况和车速情况下，能够使身垂直加速度、悬架动挠度和轮胎形变不同程度的降低，且对应的均方根值分别降低了32.73%、18.53%和15%，较为有效地改善了车辆行驶过程中各项性能指标。

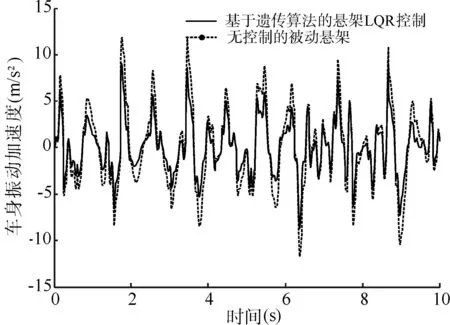
图3 车身振动加速度响应曲线

图4 动挠度响应曲线

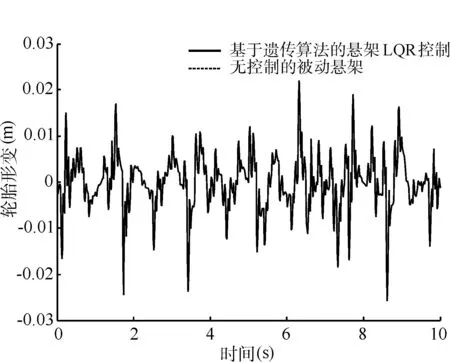
图5 轮胎形变响应曲线

5 结语

文章为改善汽车乘坐的舒适性、行驶平顺性和行驶安全性，以汽车性能指标中的车身垂直振动加速度、悬架动挠度、轮胎形变和主动控制力构建二次型最优控制目标函数，设计了LQR最优控制器。针对LQR最优控制的加权系数无确切求解方法，控制效果依赖设计者主观经验试凑加权系数问题，利用遗传算法的全局搜索能力对加权系数进行优化，大大提高了控制器的效率及性能。仿真结果证明:相比于参数不可调被动悬架系统，实施基于遗传算法权值优化LQR控制汽车主动悬架系统，在相同工况下能够使身垂直加速度、悬架动挠度和轮胎形变的均方根值分别改善了32.73%、18.53%和15%，进一步改善了汽车乘坐的舒适性、行驶平顺性和行驶安全性，该方法为汽车主动悬架系统控制策略设计提供参考。