基于融合模型的遗传位点分析∗

张继荣 寇 磊

（西安邮电大学通信与信息工程学院 西安 710121）

1 引言

遗传疾病致病位点或致病基因的提早发现，对于疾病的个性化、精准化治疗［1］有着非常重要的意义。目前全基因组关联分析，主要是借助于SNP遗传标记，进行总体的关联性分析，在全基因组范围内选择遗传性状进行基因分类，比较异常性状和对照组之间每个遗传频率的差异，总体统计分析每个异常与目标性状之间的关联性的大小，选出最具有相关性的遗传变异进行验证，并根据验证结果最终确认相关性是否存在。但是，在分析过程中进行了多重假设检验，导致假阳性的关联，降低定位的准确性，对进一步鉴别基因甚至是后续的个性化治疗造成相当巨大的偏差［2］。因此，使用精准的方法提高关联性检验的准确性［3］，降低甚至消除因多重检验造成的假阳性对全基因组关联分析有着至关重要的作用。

2 模型的建立和求解

2.1 模型假设

假设一:含有致病位点的基因属于致病基因范畴；

假设二:性状不受环境影响；

假设三:1000个样本来自同一个群体；

假设四:提供的样本为无关的个体样本。

2.2 碱基编码方式

DNA是由分别带有A，T，C，G四种碱基的脱氧核苷酸链接组成的双螺旋长链分子。所以碱基编码形式有n2（种），但是因为SNP关联分析其中有是会相互重复的，只需要保留一种［4］。所以建立数学模型:

使用直接替换的方法把原始数据中每个位点的碱基（A，T，C，G）编码方式转换数值编码方式。具体对照码表如表1所示。

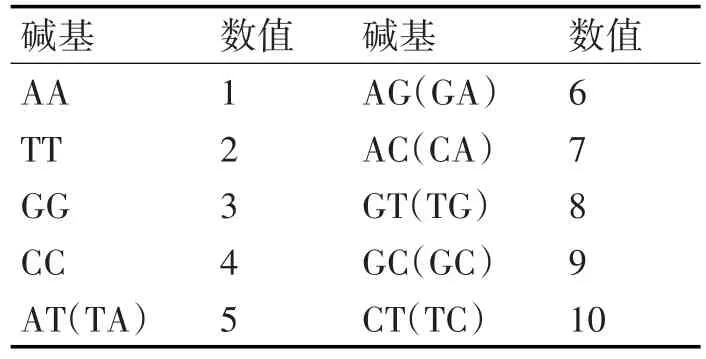
表1 碱基编码转化数值编码

2.3 SNP关联分析

利用SNP位点集搜索算法——二阶段蚁群寻找SNP位点集与遗传疾病之间的联系。此种方法使用位点集与类标间的卡方统计量作为评价函数，通过蚁群算法在可行解的空间中搜索。二阶段蚁群算法的优点是对边缘效应有高的鲁棒性，而且采用两轮蚁群算法，对这两轮的迭代过程分别设置参数［3］。

算法流程如图1所示。

二阶段蚁群算法需要指定所用蚂蚁数目iAntCount，蒸发率 ρ ，初始信息素 τ0，寻找SNP子集中位点的数目n，第一轮搜索位点数目为N1，第二轮搜索位点数目为N2以及每轮迭代次数iter_max，其中 N1＞N2＞n。在一轮迭代中，每只人工蚂蚁会按顺序选择个位点集，这组位点便是一个可行解。假设共有L个位点。某只蚂蚁在决策时是否选择位点k的概率公式为

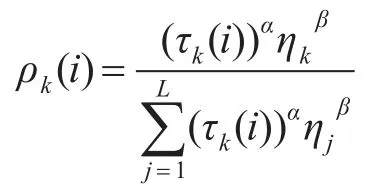
其中 τ（ki）为第i轮搜索第k个位点上的信息素［7］。但是需要注意的是，本算法中ηkβ=1，即蚂蚁在每一次选择新解时只会受信息素的影响，而忽略评价函数［8］。这么做是因为如果 ηkβ≠1，那么在每只蚂蚁选择可行解时，都需要重新计算所有位点加入后的卡方统计量，运算复杂度过高，影响算法效率，占用大量内存。在每一轮迭代结束后，每只蚂蚁都从所有K个位点中选出了一个SNP位点集，每组中含有n个位点。设蚂蚁m选择了SNP位点集Sm，则Sm中的所有位点k上的信息素会被更新，更新公式如下:

其中Δτk(i)为位点集Sm与疾病之间的0.1⋅χ2。若某位点k未在任意Sm中出现，则Δτk(i)=0。

图1 算法流程图

二阶段蚁群算法采用了两个阶段［2］的搜索策略。因为两轮搜索后的计算结果中可能包含有相同的SNP位点，所以二阶段蚁群算法对结果采用了最小化假阳率（Minimizing false positive）来进行处理。用EIall表示最小化假阳率前的结果，EIall初始化为两轮搜索后的结果，用EIm表示最小化假阳率后的结果，EIm初始化为空。对EIall中的每一个元素Ii执行以下操作:若EIm中没有元素与Ii含有相同的SNP位点，则将移动 Ii到 EIm中:若EIm中有元素Ji与Ii含有至少一个相同的SNP位点，则比较Ji与Ii，取 ρ-Value值较大的元素保留在其中，将ρValue值较小的元素丢弃。

对于二阶段蚁群的伪代码为

二阶段蚁群算法:

输入

1 for（第一轮搜索子集中的SNP位点数目，第二轮搜索子集中的SNP位点数目）

2 if setsize==第一轮搜索子集中的位点数目

3 iItCount=第一轮蚁群算法迭代次数；

4 else iItCount=第二轮蚁群算法迭代次数；

5 设置每个位点的初始信息水平

6 i=0，开始进行迭代

7 根据式（1）为每只蚂蚁选择一个含有setsize序列个位点的SNP子集，

8 计算每只蚂蚁选出的SNP子集的卡方检测统计量，

9 更新SNP子集中所有的位点上的信息素，

10 记录卡方统计量最高的SNP子集，清除蚂蚁

11 i=i+1

12 if i=iItCount停止迭代

后期处理:穷举搜索 χ2值最大的前iTopModel个子集和前iTopLoci个最大信息素子集，选出所有含有iEpiModl个位点而且阈值小于设定值的子集。

可选处理:最大限度地减少误报

返回结果:以p-Values报告所有检测到的上位相互作用。

注:其中iItCount为人工蚂蚁数；Largesetsie，Smallsetsize为两轮搜索子集中SNP位点数；iTopModel为SNP候选子集数目；iTopLoci为SNP候选位点数目；iEpiModl为SNP子集中位点数目。

2.4 Logistic回归分析

问题以位点集合为单位分别与疾病性状做关联分析，既每个单核苷酸多态性集合（Single Nucleotide Polymorphisms set，SNPs）与性状均需建立一次模型，以二阶段蚁群算法构建的SNP关联分析模型为基础，分析数据属性可以得到以下结论:

1）反应变量为二分类的分类变量或是某事件的发生率。

2）自变量与Logit（π）之间为线性关系。

3）残差合计为0，且服从二项分布。

4）各观测值间相互独立。

Logistic回归模型可以很好地满足对此类数据的建模需求。所以本文选用Logistic回归方法，并分别检测每个SNPs的显著性。

本文中探讨遗传疾病的危险因素，将选择两组人群，一组是患病组，一组是非患病组，两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否患病，即“是”或“否”（数据表示为0或1），为两分类变量，自变量就是基因包含的SNPs位点。自变量可以是连续的，也可以是分类的。通过Logistic回归分析，就可以了解哪些因素是患病的危险因素。

逻辑回归中的数据结构如表2所示，其中 y表示的是否患病，Xp表示基因中的位点信息。

表2 Logistic回归模型的数据结构

参照线性回归方程，建立下面形式的回归模型:

对分类变量直接拟合，实质上拟合的是发生概率，显然，该模型可以描述当各自变量变化时，因变量的发生概率会怎样变化，可以满足分析的基本要求。

令y=1为患病，y=0为未患病，且将患病的几率记为P，它与自变量x1，x2…，xp之间的Logistic回归模型为

由此可知未患病的概率为

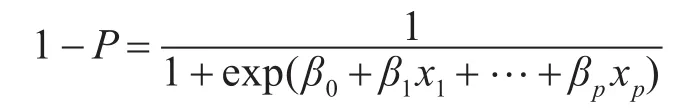
经数学变化可以得到:

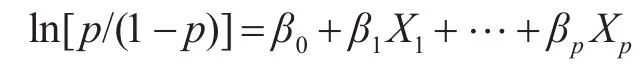
定义:

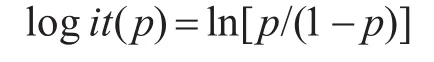
为Logistic变换，即:

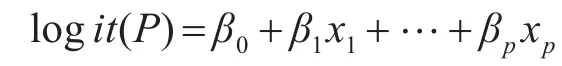
2.5 模型求解

使用二阶段蚁群算法SNP关联分析模型搜索计算得到的致病位点，如表3所示。

表3 与疾病最有可能的致病位点

由二阶段蚁群算法SNP关联分析模型输出表3，通过查找的 ρ-Value≤0.01［13］致病位点有10个，依据此10个致病位点查找尽300个基因，找出包含这些致病位点的基因。这10个基因分别是gene_102、gene_98、gene_218、gene_191、gene_260、gene_149、gene_24、gene_272，gene_84、gene_125。

计算有SNP位点构成的基因矩阵的向量间的相似度，选取与致病位点相似度最大的位点，并构成新的位点集，以该位点集来表示包含致病位点的基因，找出的位点集总共42个。通过二元逻辑回归模型求出基因与疾病的关联性。二元逻辑回归函数为

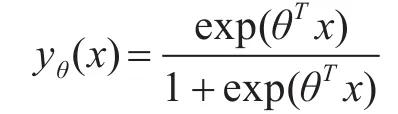
其中x为各基因为包含的位点集合，用作自变量，yθ(x)表示患病的概率。

表4 疾病与基因的关联性

3 模型检测

3.1 随机森林做模型检测

为验证二阶段蚁群算法检测到的致病位点的有效性，将这些致病位点在数据样本集（1000×9445）中提取出来作为新的验证样本集（1000×10）。由于是关于致病位点与患病与否之间的关系，因此验证致病位点有效性可以视为分类问题，本文选用随机森林算法［8］进行验证。

随机森林［9］是一种由多个决策树组合而成的分类器，它利用bootstrap重抽样方法从原始样本中抽取多个样本，对每个bootstrap样本进行决策树建模，然后将这些决策树组合在一起，通过投票或输出的平均值得出最终分类或预测的结果。

将验证样本集（1000×10）以7:3的比例随机划分为样本集和测试集，利用随机森林算法进行识别分类，通过分析实验结果，平均识别正确率达到82.15%，验证了该方法的有效性。实验结果如表5所示。

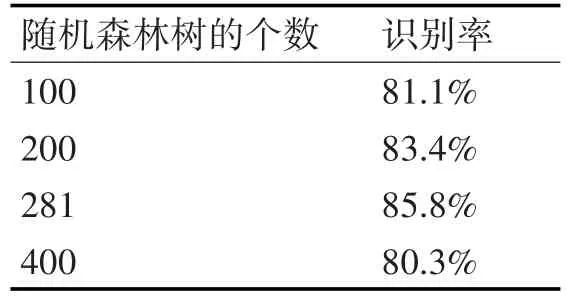
表5 随机森林检测结果

3.2 SPSS软件做模型检测

对回归模型识别率下降排序，基因的排序为gene_98、gene_218、gene_102、gene_191、gene_260、gene_149、gene_24、gene_272，选取前六个基因为与疾病可能相关的基因集合。

利用SPSS软件对逻辑回归模型进行检测［11］，将基因102、98、91、281、260、149的位点新集合输入SPSS软件中，输出一系列的模型参数，采用模型系数混合检验作为检测参数。

表6 模型系数的综合检测

模型系数的混合检验（Omnibus Tests ofModel Coefficients）是针对步骤、模块和模型开展模型系数的综合检验（如表6所示）。表6中给出卡方值及其相应的自由度、P值及Sig.值。模型卡方临界值的计算步骤如下:取显著性水平 Sig.为 0.05［13］，自由度数目为表中的df，通过查表法，可以查出卡方临界值。当表中的卡方值小于卡方临界值，Sig.值大于0.05时，模型通过检验。

表7 卡方临界值

通过计算以上各基因的卡方临界值得到表7，各基因的模型系数综合检验的卡方值均小于各自基因的卡方临界值，且各基因的显著性水平大于0.05，因此各基因的模型通过检验，验证了二元逻辑回归模型寻出与疾病最相关基因的正确性。

4 模型评价分析

为了验证模型的有效性，在本文模型的基础上和文献［7］中的传统蚁群模型与文献［12］中的Logistic回归模型进行对比。采用库都为国际标准pubmed库。模型评价采用通用准确率P评价分析［12］

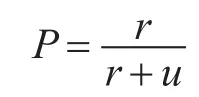
r代表检索结果中识别正确的数目，u代表检索结果中识别错误的数目。

为了验证模型的有效性和算法的合理性，在上述库中用上述模型在不同数量样本下进行识别，其准确率如图2所示。

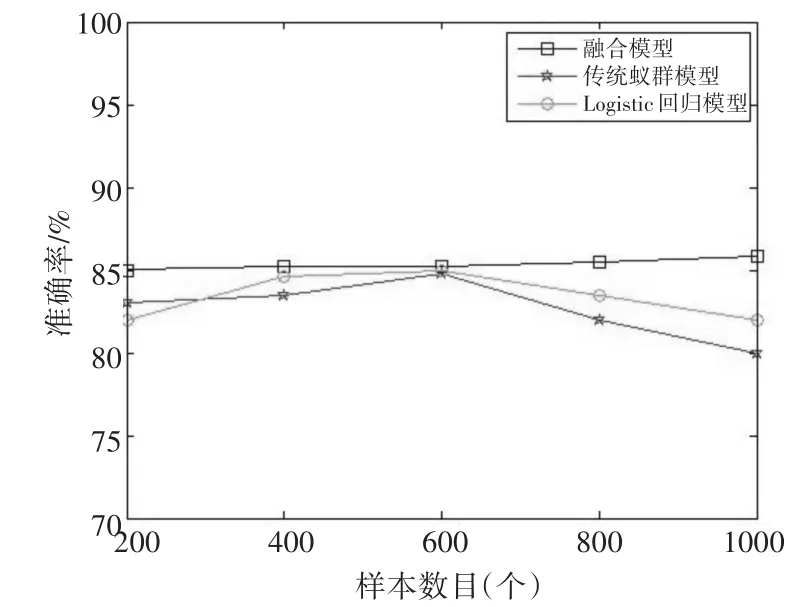
图2 五种样本数目下的准确率

由上述图像对比可知，相对于传统的遗传性疾病和性状的遗传位点分析模型，在大样本情况下，尤其是样本数目超过600个的时候，融合模型的识别准确率有显著优势。

5 结语

本文提出了一种基于融合模型的遗传性疾病和性状的遗传位点分析模型，这个模型针对基因数据的关联性特点融合不同的模型进行数据分析并综合运用各种方法得到有效的相关性分析。本文使用逻辑判断和基于条件判断的数据转换算法进行编码方式转变，在面对遗传疾病与位点的相关性，给出二阶段蚁群算法模型，得到了理想的关联性结果。在面对疾病、基因和位点多层次相关问题，通过分析之前的结果，使用逻辑回归模型中的Logistic回归模型，通过随机森林算法和卡方检测测试验证，大大加强了融合模型的可靠性。在文中所运用的二阶段蚁群算法是对基础蚁群算法的优化，在蚁群算法的信息素更新阶段加入了顺序更新的规则，分成两个阶段对蚂蚁走过路径上的信息素进行了更新，当然同时也提出了两种信息素跟新阶段的划分策略，并且把每段路径上的信息素的值限定在一个整数区间里，算法的收索能力明显增强。