基于有限元方法的测量管壁电特性与权重函数关系分析∗
2019-10-08李雪菁
李雪菁
(1.上海杉达学院信息科学与技术学院 上海 201209)(2.上海杉达学院大数据分析与处理中心 上海 201209)
1 引言
基于电磁感应理论,电磁流量计已广泛用于测量单相流中导电液体的体积流量。Shercliff[1]确定了轴向流速和感应电压的关系,并计算出了与位置有关的“权函数”(W)。W表示流动横截面上给定点的轴向流体速度对所测量的电极间的感应电位差的相对作用。W的分布特性可以作为分析与设计传感器的重要依据之一。因此权函数理论是电磁流量传感器的重要理论部分。
典型的电磁流量传感器的绝缘管道置于磁场内。在与磁场方向、管道的中心轴、管道的直径两两垂直的管道位置,装有两个与导电流体相接触的电极。典型点电极绝缘管壁电磁流量传感器基础理论已经非常成熟,因此在很多工业场合被广泛应用[2]。但有些特殊场合,比如高温流体测量,液体金属流体测量等,典型电磁流量传感器的结构就存在一定的局限性。
本文对一类特殊电磁流量传感器:非绝缘管壁电磁流量传感器[3]权重函数进行研究。“非绝缘”强调了测量管壁与其他类型电磁流量传感器的区别,即具有特定范围的电导率。具体体现在:
1)测量管的体电阻相对于被测流体足够大,即基本不影响流体感应电势大小;
2)测量管的体电阻相对于信号测量放大器的输入阻抗足够小,即保证测量精度。
由于测量管的这种“非绝缘”特性,扩大了测量管的材料选择范围,即可选半导体材料,也可选择导体材料。同时,由于测量管具有一定范围的电导率,因此可以在管壁外引出测量信号,而无需与流体接触。在磁激励作用下,便可在相应的引出线上获得流量信号。这类电磁流量传感器弥补了电磁电磁流量传感器在某些领域的应用不足。
现代工业测量对于电磁流量仪表的需求越来越多,这促使对传感器结构的研究也越来越广泛和深入。很多学者针对不同结构的权重函数都展开过深入分析。1979 年,Baker[4]计算了三种不同长弧形电极传感器在满管测量条件下的权重函数和灵敏度,对长弧形电极传感器进行了优化分析。Bate[5~6]、Teshima Taiichi[7]、Horner[8~9]等研究者对多电极传感器结构及理论进行了研究。然而,对于非绝缘管壁电磁流量传感器的权重函数讨论的很少。
2 理论背景
电磁流量传感器是基于法拉第电磁感应定律(Faraday's Law)的一种测量导电流体流量的感应式传感器。图1显示了电磁流量传感器基本工作原理。
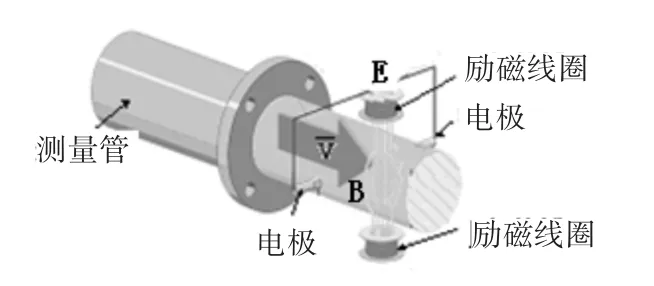
图1 电磁流量传感器基本工作原理
图1 中,绝缘管道置于磁场内。在与磁场方向、管道的中心轴、管道的直径两两垂直的管道位置,装有两个与导电流体相接触的电极。导电流体以平均速度沿测量管流动。励磁线圈在测量管道空间中产生感应磁场,磁场强度为B。在与磁场方向、管道中心轴相互垂直的位置,安装一对与导电流体接触的电极。宏观上将流体的运动看作导体在磁场内切割磁力线,当导电流体流过磁场覆盖的空间时,会在测量电极两端产生相应的感应电势E。
Bevir[10]引入虚电流的概念,具体做法如下:设U和为流体运动时产生的感应电动势和电流密度矢量,Uv和表示流体静止时单位电流通过电极时产生的电势和电流密度,由Ohm定律有


假设S1和S2是良导体制成的电极表面,τ是空间体积,在包围S的表面上(除电极外)表面法向有

由第二格林公式有

流体中的传导电流被忽略,即
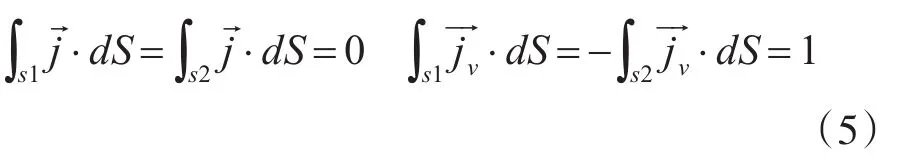
U、Uv在S1和S2上分别为常数,则最后有

其中


归一化的权重分布情况如图2所示。

图2 典型电磁流量传感器权重函数分布
图2 可看出,典型电磁流量传感器的权重函数极大值分布在两端的电极处,理论上趋向于无限,而在传感器中心处的权重函数为1,并沿着x轴两侧逐步衰减至极小值0.5。权重函数的分布特性可以作为分析与设计传感器的重要依据之一。
3 有限元仿真模型构建
有限元方法[11](Finite Element Analysis,FEA)的核心思想是结构的离散化,即将实际结构假想地离散为有限数目的规则单元组合体,实际结构的物理性能可以通过对离散体进行分析,得出满足工程精度的近似结果来替代对实际结构的分析,解决很多实际工程需要解决而理论分析又无法解决的复杂偏微分方程问题。
COMSOLMultiphysics对于基于偏微分方程建模和求解各种科学和工程问题,是一个强大的交互式环境[12~13]。根据式(1),电磁流量计可以使用COMSOL的电磁模块进行研究。
3.1 非绝缘管壁电磁流量传感器结构特点
在不影响分析结果的前提下,为降低分析复杂程度,本文对非绝缘管壁电磁流量传感器二维结构分析,如图3所示为非绝缘管壁电磁流量传感器与典型点电极绝缘管壁电磁流量传感器模型(二维)对比示意图。
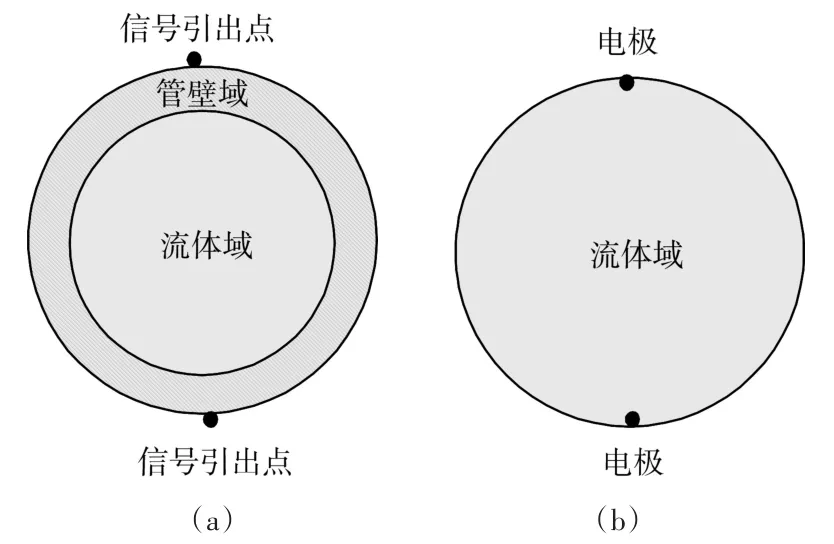
图3 非绝缘管壁与典型电磁流量传感器模型意图
如图3(b)所示,典型电磁流量传感器为绝缘管壁,且电极与流体接触。导电流体以一定速度沿测量管流动。当流体流过磁场覆盖的空间时,根据法拉第电磁感应定律,会产生感应电势。由于电极与流体接触,并且管壁(除电极外)是绝缘材料,因此电极输出的信号是流体产生的感应电势的全部反映。
如图3(a)所示为非绝缘管壁电磁流量传感器结构模型示意图。当导电流体以一定速度流过传感器管道,在磁激励作用下,产生感应电势。由于测量管壁为非绝缘材料,信号引出点上可以获得电势信号,但非绝缘管壁同时也对流体感应电势产生短路效应,使得信号引出点上并非流体产生感应电势的全部体现。
3.2 仿真算例模型的构建
在直角坐标系下,对非绝缘管壁电磁流量传感器建模如图4所示。

图4 非绝缘管壁电磁流量传感器模型
图4 中,R为管壁外半径,r为管内半径,w为管壁厚度,管壁电导率σw均匀,流体电导率σf均匀,信号引出点e(0,y)、信号引出点e'(0,-y)。在x方向设有恒稳均匀磁场(图中未画出)。
4 实验结果与分析
4.1 管壁厚度与权重函数关系分析研究
本小节通过改变R来研究w对权重函数分布的影响,设定 r=16mm,σw=0.7e6S/m,σf=1.3e6S/m。为了更具有普遍意义,本小节针对w/r对权重函数分布的影响进行定量讨论研究。有限元计算结果如图5所示。

图5 不同管壁厚度的权重函数仿真结果
仿真计算结果表明:
1)当管壁、流体电导率一定时,贡献权分布与管壁厚度有关,w增大使得感应电势的损耗就越大;
2)当w较小时,贡献权分布(如图6(a)所示),接近于典型的点电极绝缘管壁电磁流量传感器权重函数分布,验证了非绝缘管壁的权重函数分析的正确性;
3)随着w的改变,非绝缘管壁电磁流量传感器的不同位置流体微元、管壁微元随着w的变化对传感器输出信号的影响能力也将发生变化。
4.2 管壁、流体电导率与权重函数关系分析研究
本小节将通过改变管壁电导率σw(流体电导率σf保持不变),仿真研究管壁、流体电导率对权重函数分布的影响。为了更具有普适性,讨论研究对权重函数分布的影响。仿真模型如图4所示,仿真参数为R=19mm,r=16mm,w/r=0.19,σf=1.3e6S/m。
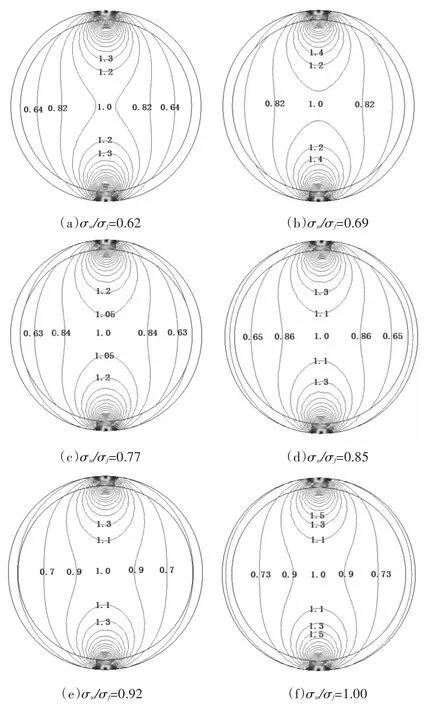
图6 不同管壁电导率的传感器权重函数仿真结果
通过图6可得:
1)当w一定时,权重函数分布与管壁、流体电导率有关,并且距离信号引出点位置较近的微元权重函数值较大,符合基本的理论分析结论;
2)σw与 σf相等,即 σw/σf=1.00时,权重函数分布(图6(f)),与典型的电磁流量传感器权重函数分布一致,也验证了非绝缘管壁电磁流量传感器权重函数的正确性;
3)随着 σw/σf的改变,管壁、流体区域的权函数分布都会发生改变。这是因为传感器内有一个单位的虚电流,管壁、流体电导率比的改变影响虚电流密度在管壁区域及流体区域的分布。故管壁、流体的电导率同样可以改变流体微元、管壁微元对于传感器输出信号的影响能力。
5 结语
有限元计算结果证实了非绝缘管壁电磁流量传感器权函数的分布受管壁电特性的影响。随着管壁厚度的减少,管壁区域内的虚电流分布增加;随着管壁电导率的增加,管壁区域内的虚电流分布增加。即接近典型电磁流量传感器。本文的研究结果不但填补了对非绝缘管壁电磁流量传感器的理论空白,而且对于传感器的设计加工具有一定的指导意义。
