小学数学教学中转化思想的渗透分析
2019-10-07石开勇
石开勇
摘 要:小学数学的学习需要转化思维,因此数学教师要通过新旧知识相互穿插,形成转化意识;合理运用假设方式,助推学生思维进行转化;数形转化的应用,创新思维模式,进而提高小学生的数学学习能力。
关键词:小学数学教学;转化思想;的渗透分析
数学知识的抽象性是众所周知的,而对于小学生来说,要学习这种抽象性强的知识,必须具备一定抽象思维和逻辑思维,但是小学生的逻辑思维还不是很活跃,形象思维则比较活跃,因此小学数学教师要想一些办法,帮助学生转化数学知识,形成转化思维,以此更好地学习数学知识。在小学数学教学中,教师渗透转化思想,帮助学生快速解题,提高学习效率。数学教师运用各种方式,训练学生的转化思维,从而促进学生全面发展。
一、新旧知识相互穿插,形成转化意识
新知识的学习,是在旧知识掌握的基础上,通过新旧知识的穿插,能够更好地强化学生对已经掌握知识的激活,形成新旧知识之间的练习,运用已经掌握的知识,转化成为新的知识,从而形成转化意识,逐渐形成转化思维。如同几何知识的学习,小学数学教材内容涉及到很多图形几何知识,各种图形的面积,会逐渐学习到长方形、正方形、三角形、平行四边形、梯形等图形面积的计算方法。在学习的过程中,教师需要将长方形面积公式作为基础,将其贯穿在其他图形面积公式的教学中。长方形面积公式则是非常重要的内容,将其引入到其他图形面积公式的教学中,体现出了转化思想。数学教师运用转化教学:多媒体上展示平行四边形,由很多小方格组成,引导学生数一数有多少个小方格?每一个小方格是1平方米,不满一格的均按半个计算,问这个平行四边形的面积是多少平方米?学生数完后,得出平行四边形的面积是24cm2。然后展示出一个长方形,也由小方格组成,让学生数一数并算一算长方形的面积是多少,学生数完得出长方形长为6cm,宽为4cm,面积是24m2。问学生:你发现了什么?学生通过比较、讨论,得出:两个图形的底与长,高与宽和面积分别相等。在多媒体上,展示出平行四边形变成长方形的推导过程,然后并让学生拿出自己的学具平行四边形纸片,像刚才演示的操作一样,同桌相互合作,动手进行剪、拼、移的操作方法,从中再次验证一下是否正确,教师巡回指导学生的操作。同时引导学生思考:通过刚才的操作演示你发现了什么?学生可能会回答:我发现把平行四边形的面积转化成长方形后形状变了,但面积没有变,即长方形面积就等于平行四边形面积。同学发现长方形的长就是平行四边形的底,宽就是平行四边形的高,进而引导学生利用长方形的面积公式,推导出了平行四边形面积的计算公式,平行四边形的面积=底×高。
二、合理运用假设方式,助推学生思维的转化
小学生学习数学时,受到数学知识逻辑性的影响,当学生遇到一些比较有难度的问题时,自己不知道该用什么样的思维解决这些问题,也就停止了学习脚步。所以,小学教师组织教学活动的时候,要运用合理的方式,帮助学生形成转化思维,将抽象的问题,转化成为具体的问题,通过假设的方式,让学生掌握到问题中的重点,让学生找到解题的入口,掌握问题重点,才能快速地解决问题。比如,速度问题中,问题是小红和小美进行赛跑,他们所用的时间是一样的,路程也是一样的,但是两个人的速度不同,小红比较快,小美比较慢,小红的速度比小美的速度快20%,小美则比小红的速度慢30%,请问两人跑步的速度分别是多少?在没有具体时间和路程的情况下,学生们在解决这个问题时,有些手足无措,但是教师运用了假设的方式,提出一些假设条件,然后解答出问题的答案。假如说两个人所跑的路程都是500米,这样就将抽象的问题,变成的具体的问题,学生会算出答案。借助假设的方式,解答数学逻辑问题,转化思维的作用凸显出来,问题具体化、简单化,学生理解起来就更加容易。
三、数形转化的应用,创新思维模式
具体的、形象的思维,是小学生思维特点,因此在教学中渗透转化思维,教师要能运用具体事物将数学抽象知识表现出来,数形转化就是非常好的代表,将数字通过具体的形状或者形体展现在学生面前,从而帮助学生理解数学问题或者知识,把复杂数量关系,转化成简单的形象问题,这一过程就是转化的过程,学生理解起来更加容易,进而提高解题速度。
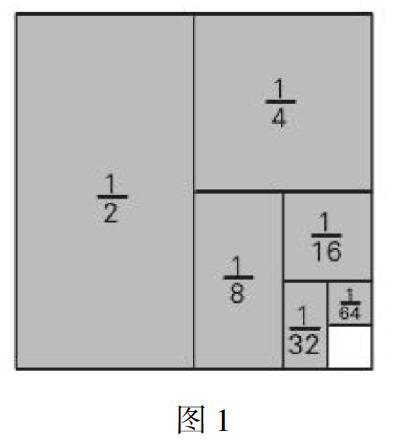
例如,分数的计算中,在一连串分数的计算中,教师可以运用数形转化的思想,通过图案将每个分数表示出来,方便学生们理解,让一些抽象的数字变得具体化,以新颖的方式展示给学生,学生固有思维模式被打破,也有利于培养学生的创新思维。像1/2+1/4+1/6+1/8+1/16+1/32+1/64,将这些数用一个正方形表示出来,如图1,阴影部分就是和,就整个正方形,看成是单位1,减去空白部分1/64,也就是63/64。这种转化思维的渗透,不但提高了解题速度,还培养了学生创新能力。
结束语:综上所述,小学数学中教师要逐渐渗透转化思维,通过合理的方式,幫助学生形成转化思维,进而形成数学学习意识,提高学习能力,全面地发展。
参考文献:
[1]李桂芹.小学高年级数学教学中转化思想的渗透与运用[J].数学学习与研究,2018(20):80.
[2]廖秀芳.教有所思 学有所想——转化思想在小学数学教学中的渗透[J].福建基础教育研究,2018(06):86-87.
