山东省区域经济差异分析
2019-10-06左韶泽
左韶泽
摘 要:城市的经济发展水平是一个城市发展水平的重要体现,但由于各方面的原因,城市间的经济发展水平差异越来越大。选取能够体现经济发展水平的8个变量,利用因子分析的方法对山东省17市的经济发展水平进行综合分析。之后对得到的因子得分进行聚类,将17市划分为3个类别,分析不同类别之间的差异和影响因素,并对区域经济的协调发展提出一些建议。
关键词:区域经济;因子分析;聚类分析
中图分类号:F2 文献标识码:Adoi:10.19311/j.cnki.1672-3198.2019.29.001
1 前言
山东省位于渤海与黄海之畔,是中国著名的经济强省之一。2018年山东省的生产总值高达7.6万亿元,在全国排名第三。改革开放以来,全省经济持续快速发展,成为中国经济不可或缺的一部分,这与山东各市的贡献是分不开的。但由于多方面的原因,省内区域经济发展差异显著,尤其是在近些年来有进一步拉大的趋势,这也将成为制约山东经济发展的一个重要问题。因此本文选取2017年山东省17市体现经济发展水平的相关数据,采用因子分析和聚类分析来探索不同城市的经济发展情况,找到一些对山东省的区域经济差异造成影响的公共因素,借助这些公共因素,对山东各市的经济差异进行一个客观的评价,并且找出造成这种经济差异的主要原因。最后希望能通过分析,提出一些行之有效的方法,能够有利于山东省区域经济的协调发展。
2 模型介紹与指标选取
2.1 模型介绍
因子分析的基本思想是根据相关性的大小对原始变量进行分组,使同一组内变量之间的相关性较高,不是同一组的变量间的相关性低。每组变量都是一个基本结构,用一个综合变量表示,这个基本结构被称之为公共因子。对所研究的一个具体问题,原始变量可以分解成两部分之和的形式:一部分是不可观测的公共因子的线性函数;另一部分是与公共因子无关的特殊因子。聚类分析则是按照某种距离计算方法,对个体或对象分类,使得同类对象相似性最高,异类对象差异性最大。
2.2 指标选取
本文选取了X1-工业总产值、X2-就业人数、X3-城镇人口数、X4-地区生产总值、X5-公共预算收入、X6-在岗职工工资总额、X7-住宿餐饮业就业人数和X8-货运总量8个指标,所有数据均来自《山东统计年鉴2018》。其中X2、X3、X6是反映城市规模的指标,X1、X8反映的是工业发展规模,X7反映第三产业的规模,X4、X5在一定程度上反映了国民收入水平。
3 因子分析
3.1 数据检验
因子分析是为了从众多的原始变量中综合出少数几个具有代表性的因子,这其中有一个要求,原有的变量间应当具有较强的相关关系。因为如果变量间的相关关系弱的话,就无法从原始变量中综合出反映某些变量共同特性的几个较少的公共因子。因此在进行因子分析前,需要对原始的变量是否相关进行检验。检验结果显示,所有相关变量的相关系数都大于0.3,大部分相关变量的相关系数较高,各变量具有较强的线性相关关系。巴特利特球度检验统计量的观测值是240.796,相应的P值接近0。把显著性水平α设为0.05,则相应的概率P值小于显著性水平α,应当拒绝原假设,认为相关系数矩阵与单位阵有显著差异。同时,KMO值为0.731,符合KMO度量标准,所以原始变量适合进行因子分析。
3.2 因子提取
在对原始变量进行相关性检验后,就应该求解因子载荷矩阵进行因子提取了。因子载荷矩阵的求法很多,本文使用的是在因子分析中占主要地位的主成分分析法。主成分分析法能够为因子分析提供初始解,因子分析是对主成分分析的扩展与补充。主成分分析法的核心就是通过原有变量的线性组合以及各个主成分的求解来达到对原始变量的降维目的。因为本文选取的变量数量级差异很大,而且单位不同,所以采用相关系数矩阵作为提取因子的依据。进行因子提取后,根据因子的累计方差贡献率来确定因子个数。一般选取累计方差贡献率大于0.85时的特征值个数为因子个数k。本文提取了2个主因子,累计方差贡献率达到了93.6%,基本体现了原始变量中所有的信息。
3.3 因子旋转与命名
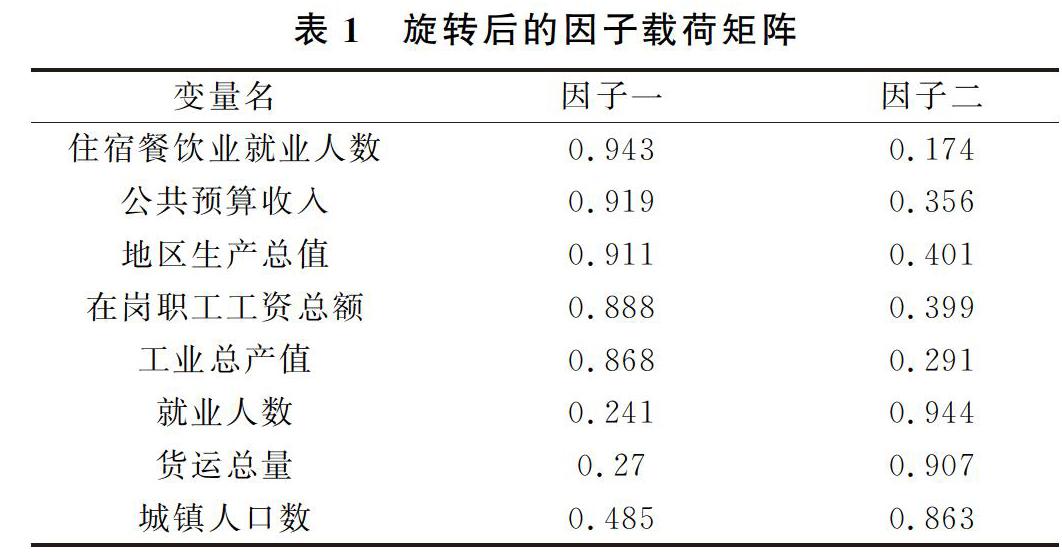
建立因子分析模型的目的不仅仅在于找到公共因子,更重要的是对公共因子进行解释,能够更加容易的分析实际问题。然而,得到的初始因子解各主因子的代表变量常常不是很突出,容易造成因子意义含糊不清的后果,不容易分析实际问题。因此,可以对初始公共因子进行线性组合,通过线性组合来找到意义明确,更容易被解释的公共因子,这就是因子旋转。因子旋转可以被分为正交旋转和斜交旋转,二者各有优劣。本文选用的是正交旋转方式中的方差极大法,以便使因子更容易被命名解释。旋转后的因子载荷是按照第一个因子降序的顺序输出的,旋转后的因子载荷矩阵如表1。
从表1可以看出,住宿餐饮业就业人数、公共预算收入、地区生产总值、在岗职工工资总额、工业总产值在第一个因子上的载荷都大于0.85,这几个变量主要被因子一解释,可以理解为对山东省内区域经济差异的直接影响因素,因此命名为经济发展因子;就业人数、货运总量、城镇人口数在第二个因子上的载荷都大于0.85,因子二主要解释了这几个变量,可以理解为对区域经济差异的间接影响因素,命名为持续影响因子。经过旋转后,各个变量的因子含义更清晰。
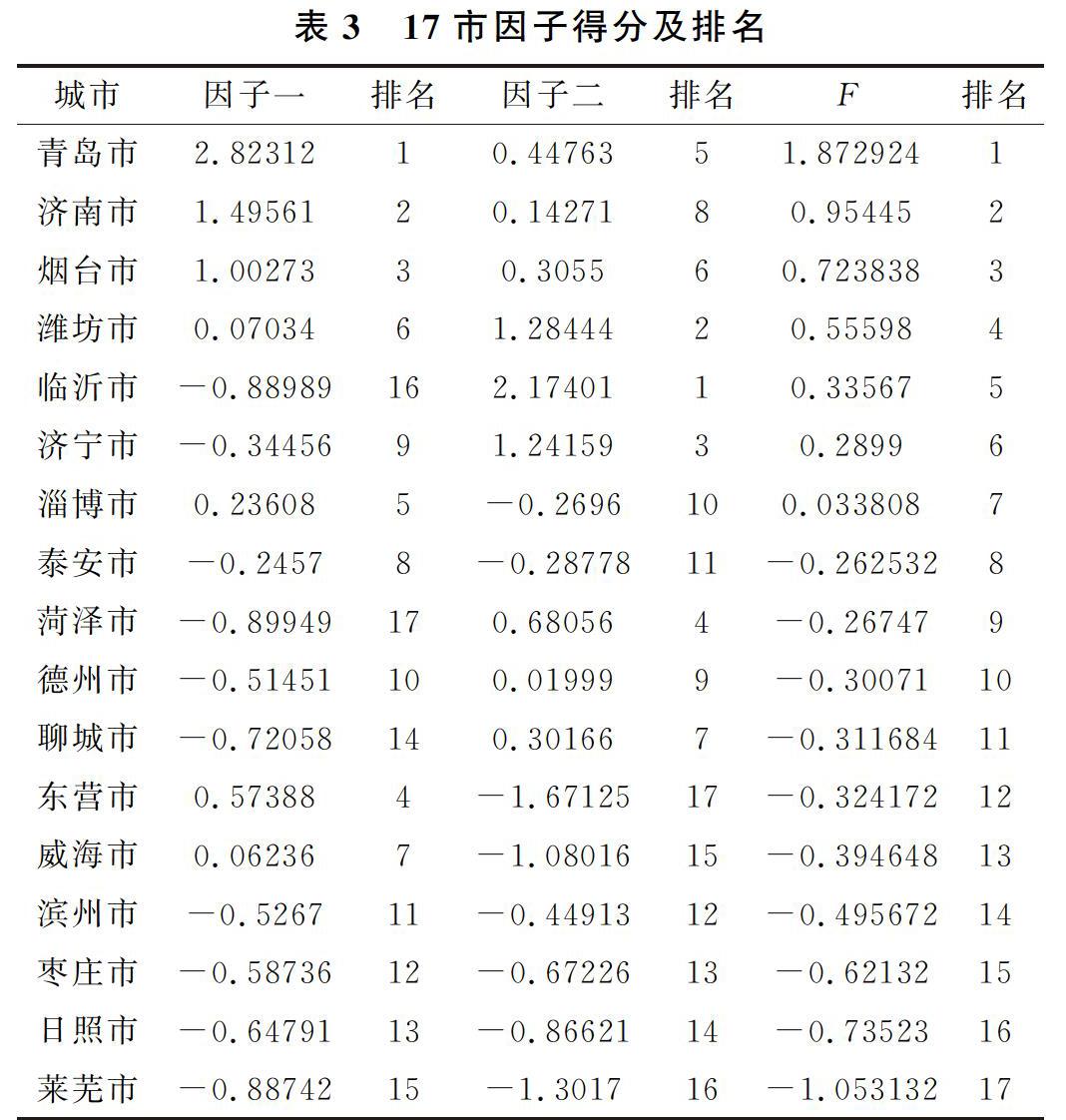
3.4 计算因子得分
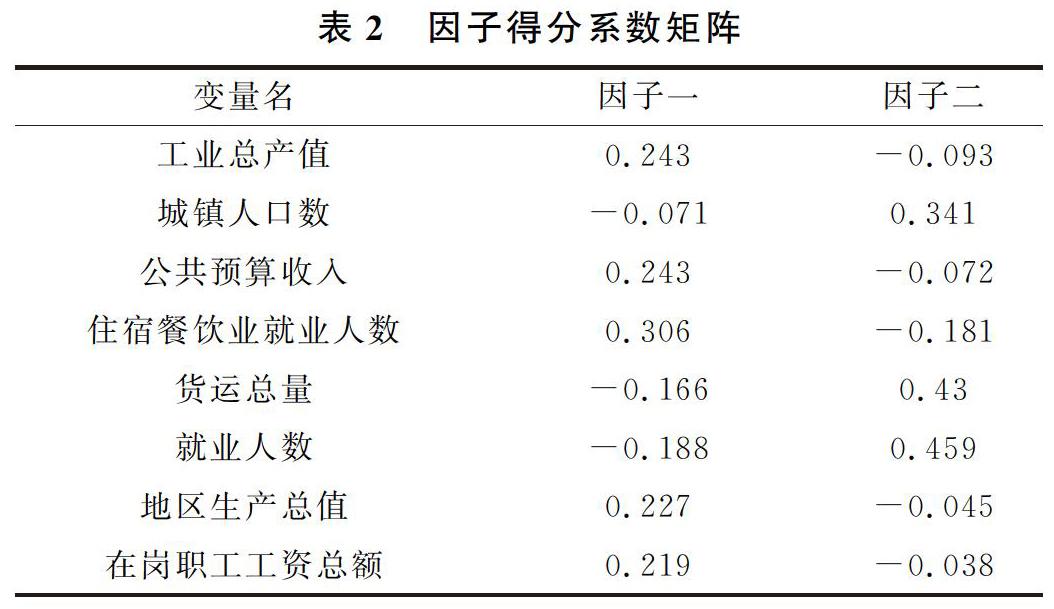
在建立因子模型后,就要反过来考察每个样品的性质和样品间的关系。比如在建立了关于区域经济差异的因子模型后,就想要知道哪些区域经济发展好,哪些区域经济发展较差等,这就要进行因子分析的关键一步,即计算因子得分。因子得分也是因子分析的最终体现,需要计算各个因子在每个样品点上的具体数值,这些数值就是因子得分,由此形成的变量也被称之为因子得分变量。在以后的分析中,就可以直接使用因子得分变量来研究样品的评价或对其进行分类了。本文采用回归法计算因子得分系数,得分系数的均值为0,标准差为1,大于0证明比平均水平高,小于0表示比平均水平低,计算结果如表2。
