等价转化思想在高中数学解题中的应用
2019-10-06吕丽
吕丽
【摘要】解答高中数学问题时,有效利用等价转化思想,可做到将直接问题间接化、复杂问题简单化,能够大幅度提升学生的解题效率。针对等价转化思想在高中数学解题中的应用,展开了探讨,并列举了一些等价转化思想的实践应用例子,希望可以为有关研究提供一些参考。
【关键词】等价转化思想 高中数学 解题 有效策略
等价转化思想主要指具体解答数学问题的过程中,基于个别方式降低问题难度,提升问题解答效率的一种思路。从本质意义上来讲,等价转化思想即为一种数学思维能力,具体开展等价转化时,通常需要化困难为容易、化繁琐为简单,通过合理变化、整合原有问题的方式,将其转变为解答者熟悉的简单问题,以此来提升解题的实效性。
一、等价转化思想在高中数学解题中的应用分析
(一)直接问题间接化
解答个别数学问题的过程中,由于其分类情况较多,解答难度较大,学生出现重复或者遗漏问题的可能性较高。针对此类问题,在正面分类情况相对较多时,那么反面情况通常相对较少,所以,可利用间接法开展具体的解答操作,能够大幅度提升解题的便捷性。
(二)复杂问题简单化
针对个别数学问题而言,直接利用正面解答的方式,解题的难度通常较大,如果可以经由转变问题思考解读或者解答思路的方式,通常可以使得问题的复杂性大幅度降低,有助于更高效的解答问题。


具体解答此类问题的过程中,一般会应用给出条件开展合理的变化操作,利用给出条件对未给出条件进行转化,利用固定的方式解决相应问题。其中需要注意的是,需要重视分析给出条件及结论间存在的关联,寻找到隐含条件,促使复杂问题简单化,提升解题便捷性。
(三)应用要点
1.合理设计转化目标
等价转化思想是一种思维能力,主要应用流程包括明确对象、设计目标,择选方法。其中,设计目标这一环节具有的重要性较高,也是等价转化思想应用过程中难度最大的环节。所以,有效开展目标的设计操作十分关键,在具体设计目标的过程中,一般会选择范化问题,包括基本公式及基础知识等当作依据。
2.充分考量转化方法特点
在设计完转化目标之后,需要科学设计转化方法,针对同一个转化目标,可应用的转化方法及手段较多,且多具有较大差异性,倘若无法有效选择,则可能导致解题的难度及复杂性大幅度提升,进而无法完成解题操作。所以,应注重择选或者设计出便捷、科学的转化方法。
3.注重转化等价性
一般情况下,可将转化分为两种,包括等价转化以及非等价转化,通常对等价转化的应用较多,等价转化的依据普遍为有关充要问题。但多数高中数学问题中均不会对充要条件进行统一表述,此为等价转化时致使各种逻辑性问题出现的主要原因。基于等价转化思想解决数学问题,主要指将所需要解答的问题转化为可高效解答问题的一种方式。
经由合理转化的方式,将复杂、解答难度较大的问题,转化为简单、可快速解答的问题。等价转化思想在高考中出现的几率较高,因此,高中数学教师有必要教导学生良好的掌握等价转化思想,并引导其树立起优良、主动的转化意识,有助于大幅度提升其解决数学问题的灵活性,进而更高效、准确的解答数学问题。
等价转化思想存在较高多样性及灵活性,在将其应用于数学问题解答中时,并没有一个固定的模式。其可以为数、形间的转化,也可以是数、数间的转化;可以在符号系统内进行转化,也可以基于宏观角度开展等价转化。数形结合法以及消去法等,均对等价转化思想具有不同程度的体现。换而言之,等价转化即为把恒等变形从代数式的形变升级为维持命题真假不发生变化。
二、等价转化思想在高中数学解题中的实践应用
(一)在不等式问题中的应用
不等式是学习高中数学的过程中必须掌握的知识之一,具有较高的重要性,和方程及函数等均存在较为紧密的关联,一般来讲,可经由将不等式类问题等价转化为方程及函数类问题的方式,基于题目内容合理开展函数的设计操作,再经由研究辅助函数的方式,结合函数的性质开展相应的解题操作,有助于降低问题难度,提升解题效率。
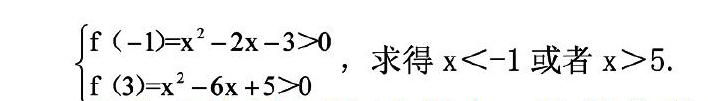
解答上述例题的过程中,将等价转化思想作为基础,将参数变元a当作主变元,将变元x当作系数内的参变元,合理设计出a相关的一次函数,再使用单调性求解的方式对其加以解答,具有较高的灵活性。
(二)在解方程中的应用
方程类问题在高中数学中具有的重要性较高,在具体解答此类问题的过程中,通常会利用将无理方程转化为有理方程、将分式方程转化为整式方程等方式,在具体解答方程类问题时,科学应用等价转化思想,有助于提升解题实效性。
三、结束语
综上所述,合理应用等价转化思想,对促进高中阶段学生数学解题效率提升,具有积极影响。教师理应对培养学生有效应用等价转化思想解答数学问题的能力提起高度重视。同时,应注意的是,等价转化思想存在较高灵活性,在实际应用此类思想的过程中,教师应引导学生优先对等价转化的思路及方式加以有效设计,避免其出现解题失误的问题。
参考文献:
[1]杨丽娴.掌握正确方法,加强逻辑引导——论高中数学教学中学生解题能力的培养[J].数学教学通讯,2018,(30) :65.
[2]廖金祥,傅磊,王成焱.高中数学教师解题的思维固化及其对策——一道教師技能大赛试题引发的思考[J].福建基础教育研究,2018,(07) :47.
[3]赵临龙.模型、联想、转化:数学解题创新的关键点——2009年全国高中数学联赛陕西赛区预赛一道几何题的证明[J].中学数学研究,2018,(07) :33.
