扶壁式挡墙抗采动变形性能优化研究
2019-09-28吴振张春丽
吴振 张春丽


摘 要:本文应用ANSYS 有限元分析软件,通过对采动区扶壁式挡墙采用数值模拟计算得出了合适的竖板厚度、底板厚度、挡墙长度和扶板间距,为扶壁式挡墙的设计提供有效的依据。
关键词:采动区;扶壁式挡墙;数值模拟;优化研究
中图分类号:U417.1 文献标识码:A 文章编号:1006—7973(2019)08-0108-02
1引言
近几年来,随着我国经济建设的发展,道路建设越来越多,然而由于我国矿产资源丰富,在这些资源被开采所造成的地表变形会对道路造成影响。目前对于扶壁式挡土墙的研究,主要集中在传统高填方边坡上,对于采动区高填方边坡支挡研究较少。本文利用ANSYS有限元软件,通过建立三维模型,对扶壁式挡墙结构在采动状态下进行研究,得出挡墙竖板厚度、底板厚度、挡墙长度和扶板间距变化时挡墙的最大主应力变化规律,为扶壁式挡墙的设计提供有效的依据。
2有限元计算模型的建立
2.1 基本假设
(1)采用三角函数法施加在模型的底边界上用以模拟采动影响下的地基不均匀沉降。
(2)不考虑孔隙水压力的影响。
(3)为简化模型计算,地基土为一种土体,土体为均质各向同材料。
2.2 计算模型
ANSYS所建模型包括挡土墙、土体等主要部件。根据扶壁式挡墙的设计特点和工程条件,单段挡墙高度为10m,墙趾宽2m,墙踵宽度4m,挡墙竖板厚度,底板厚度,挡墙长度和扶板间距为变化值。挡墙下两侧土体长度各取40m,挡墙下土体高度20m。如图1所示。
2.3 计算参数
本模型材料计算参数见表1。
3 计算结果与分析
为消除先期固结应力的影响,使用先导出初应力,再将其导入的方法。在考虑重力作用的情况下,可以保证所建模型的尺寸和初始应力状态与实际情况相符。运用数值模拟方法,分别研究挡墙竖板厚度,底板厚度,挡墙长度和扶板间距变化时挡墙的最大主拉应力变化规律,从而得到挡墙的最优化结构数值。主要分成四个部分:
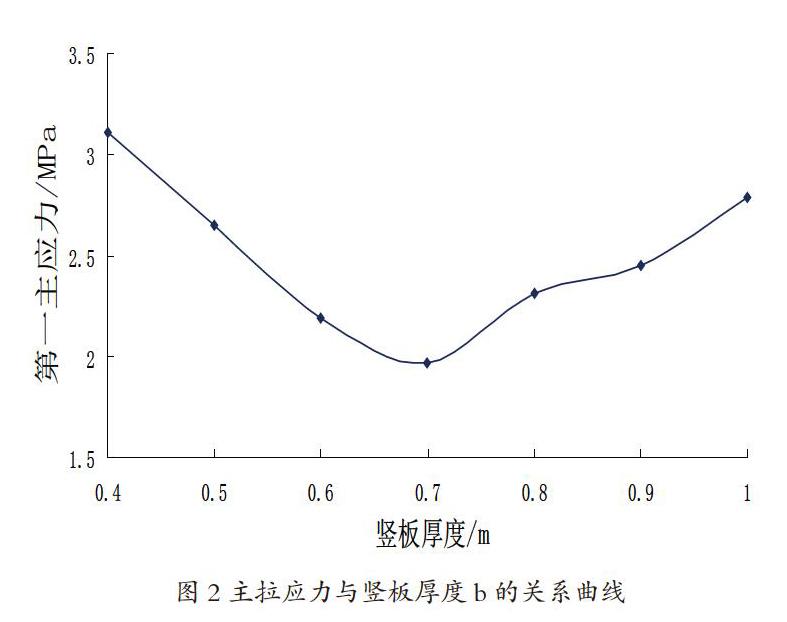
(1)图2挡墙高度和长度一定,挡墙竖板厚度变化的情况,竖板厚高比b/H分别取0.04~0.1。
(2)图3挡墙高度和长度一定,挡墙底板厚度变化的情況,底板厚度h分别取0.4~1.0。
(3)图4挡墙厚度一定,挡墙长度变化的情况,长高比L/H为0.7~1.3。
(4)图5挡墙厚度和长度一定,挡墙扶板间距变化的情况,扶板间距D与挡墙长度比值D/L分别取0.1~0.7。
由图2可以看出,挡墙高度和挡墙长度等不变的情况下,当调节竖板厚度时,最大主拉应力分布曲线呈先减小后增大的趋势,扶壁式挡墙在竖板厚度b为0.7m时,主拉应力最小且在结构等效最大拉应力范围内。
由图3可以看出,挡墙高度和挡墙长度等不变的情况下,当调节底板厚度h时,最大主拉应力分布曲线呈先减小后增大的趋势,扶壁式挡墙在h为0.8m时,主拉应力最小且在结构等效最大拉应力范围内。
由图4可以看出,挡墙高度和厚度等不变的情况下,当调节挡墙长度时,最大主拉应力分布曲线呈先减小后增大的趋势,扶壁式挡墙在挡墙长度L为10m时,主拉应力最小且在结构等效最大拉应力范围内。
由图5可以看出,挡墙竖板以及底板厚度和挡墙长度等不变的情况下,当调节扶板间距时,最大主拉应力分布曲线呈先增大再减小后增大的趋势,扶壁式挡墙在扶板间距D为3m时,主拉应力最小且在结构等效最大拉应力范围内。
4 结论
本文应用有限元数值模拟及其理论分析等方法,对采动区扶壁式挡墙抗变形结构进行研究,得出以下主要结论:
(1)在负曲率变形作用时,扶壁式挡墙在竖板厚高比b/H为0.07时,主拉应力最小且在结构等效最大拉应力范围内。
(2)在负曲率变形作用时,扶壁式挡墙在底板厚度h为0.8m时,主拉应力最小且在结构等效最大拉应力范围内。
(3)在负曲率变形作用时,扶壁式挡墙在挡墙长高比L/H为1.0,D/L为0.3时,主拉应力最小且在结构等效最大拉应力范围内。
参考文献:
[1] 柏永生.采动区双面加筋土挡墙力学特性研究[D]. 江苏徐州,中国矿业大学,2008.
[2] 陈桂林. 桩承扶壁式挡墙在深厚填土地基中的应用[J]. 福建建设科技, 2009,6:15-17.
[3] 李永树,韩丽萍.采动沉陷对建筑物的破坏作用[J]. 河北煤炭建筑工程学院学报, 2004,2:48-51.
[4] 煤炭科学研究总院唐山分院.抗变形结构理论计算方法[J]. 1993: 24~40
[5] 马石城,邹银生,王贻荪. 不同土压力下悬扶壁式挡土墙抗倾覆稳定比较[J]. 建筑科学,2006,16(6):117-121.
