基于虚拟调制指数集的多指数CPM 减相位状态检测

谢顺钦，周锞，陈大海，李湘鲁，钟声，张健

（中国工程物理研究院电子工程研究所，四川 绵阳 621999）

连续相位调制（CPM,continuous phase modulation）是一种高带宽效率的恒包络调制体制[1]。多指数CPM（Multi-hCPM）与单指数CPM 相比，增大了信号的最小欧氏距离，提升了基于相干网格状态检测的误码性能。美国先进靶场遥测组织在遥测标准IRIG106-04[2]中已将Multi-hCPM 信号定义为新一代的遥测信号，以取代频谱效率低下的脉冲编码调制/频率调制（PCM/FM,pulse code modulation/frequency modulation）遥测体制。虽然Multi-hCPM 具有频谱利用率高和功率效率高的优点，但其接收端存在两大难点——同步困难及解调复杂度高，为降低接收端的复杂度，本文提出了低复杂度检测算法。

Multi-hCPM 为有记忆调制信号，其最佳接收为最大似然序列检测（MLSD,maximum likelihood sequence detection）[1]，而Multi-hCPM 的特性，如进制数高、调制指数小以及部分响应长等，造成其MLSD 的检测复杂度很高，主要表现在接收机的匹配滤波器规模和序列检测的网格状态数两方面。因此，针对Multi-hCPM 的复杂度简化算法主要是从这两方面着手，基于匹配滤波器的简化方法主要有基函数分解[3-4]、脉冲幅度调制（PAM,pulse amplitude modulation）分解[5]及频率脉冲截断（FPT,frequency pulse truncation）[5]等；网格状态数的简化又可以分为相关状态简化和相位状态简化两方面，减状态序列检测[6]（RSSD,reduced state sequence detection）以及PAM、FPT 都能完成相关状态的简化，而简化相位状态的方法目前仅有基于相位状态合并的RSSD[5]。因此，与相关状态的简化方法相比，从简化相位状态出发的低复杂度检测方法较为单一，且RSSD算法在接收端需要基于MLSD的状态网格进行匹配滤波，因此无法简化匹配滤波器的规模。

最近的文献[7-8]针对单指数CPM 提出了一种新的简化相位状态的算法，该算法在接收端构造虚拟的且分母更小的调制指数，并结合逐幸存路径处理（PSP,per-survivor processing）能够有效简化网格状态中相位状态。本文将该方法扩展到Multi-hCPM，构造多组基于虚拟调制指数集的简化接收方案。最后将本文算法与FPT 算法（FPT 算法可简化匹配滤波器和相关状态，但无法简化相位状态）联用，更大程度地简化了Multi-hCPM 的接收复杂度，并验证了本文算法与其他简化算法联合使用的适应性。

2 系统模型

2.1 Multi-hCPM 信号及其倾斜相位表示

Multi-hCPM 基带信号的相位可以表示为[1]

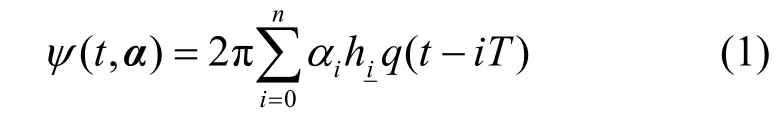
其中，T为符号周期；αi∈{± 1,±3,…,±(M-1)}，M为调制进制数；有理数hi=为i时刻的调制指数，下标=RH(i)，RH(·)为模H操作，H为调制指数集的元素个数；q(t)是CPM 频率脉冲g(t)的积分，g(t)长度为LT。除特殊说明外，本文针对M=4，L=3，g(t)为升余弦脉冲，h=的双调制指数（H=2）CPM 信号，即IRIG106 中定义的Multi-hCPM，以下简称Tier2 信号。

加入倾斜相位分解[9]后，式(1)可表示为

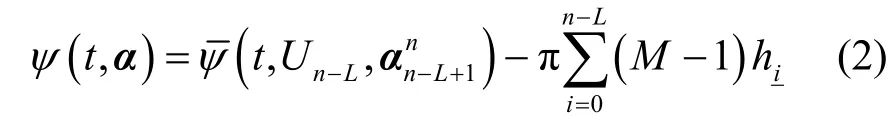
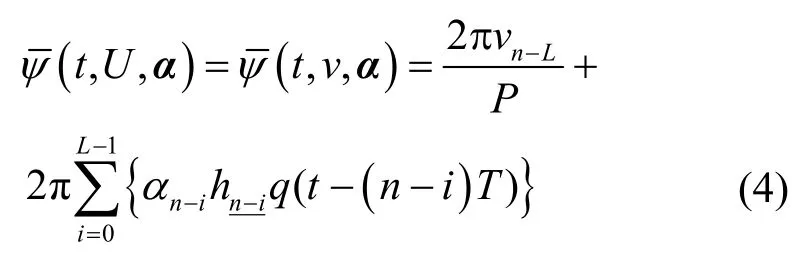
在物理相位下，vn满足递归表达式，如式(5)所示。

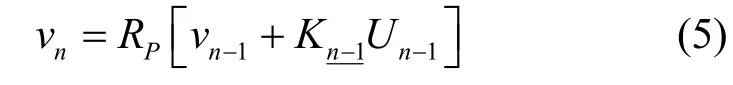
其中，RP[·]为模P操作，Kn和Un为整数。因此vn共有P种离散的可能值，在倾斜相位下，相位状态数由MLSD 网格中的2P降低为P。

2.2 Multi-hCPM 信号的MLSD 及复杂度分析

CPM 信号的最佳接收——MLSD 是基于网格状态转移和维特比算法实现的，在第n个符号间隔内，CPM 的网格状态（向量）定义为

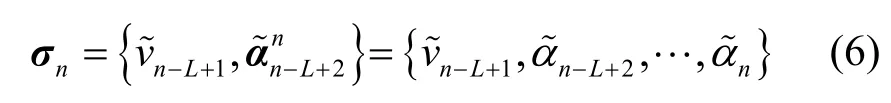
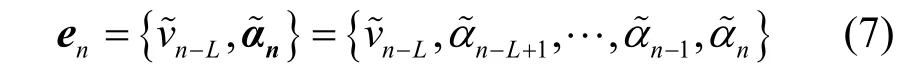
在nT时刻的所有分支度量增量表示为

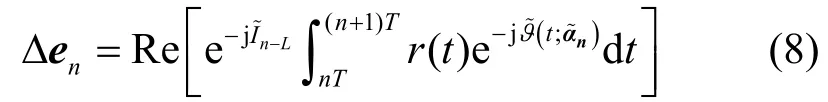
对于Tier2 信号，P=16，M=4，L=3，因此即使在倾斜相位模型下，网格状态数Nst=256，在目前常用的FPGA 硬件资源下很难实现这一检测复杂度，因此Multi-hCPM 工程实现的第一步是采用低复杂度算法降低其检测复杂度。

3 算法描述

3.1 虚拟调制指数检测原理

调制指数通常由有理数构成，其分母决定了接收网格的状态数。Multi-hCPM 为了在较小的调制指数集中实现元素的差异性[1]，调制指数的分母通常较大，如Tier2 信号的调制指数分母为16。

采用虚拟调制指数降低检测复杂度的思想由Messai 等[7-8]针对单指数CPM 提出，Messai 将其称为基于PSP 的最优检测。接收端采用不同于调制端的调制指数，当接收端的调制指数分母相比真实调制指数的分母小时，可以降低状态网格中的相位状态数。本文将该算法推广到Multi-hCPM 信号，并对算法的部分原理进行了调整，为区别于单指数CPM 的方法，将其称为基于“虚拟调制指数集”的低复杂度检测（VhD,virtual indexes(h)detection）。

设接收端的调制指数为

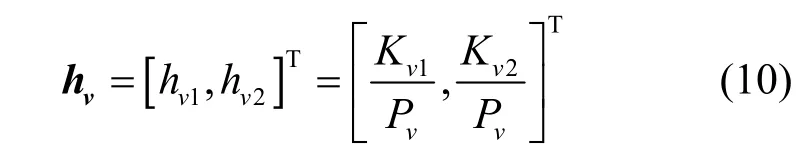
其中，Pv为整数，Kv1、Kv2为小于Pv的整数。与真实调制指数h=[h1,h2]T之间存在着调制指数差异Δh。

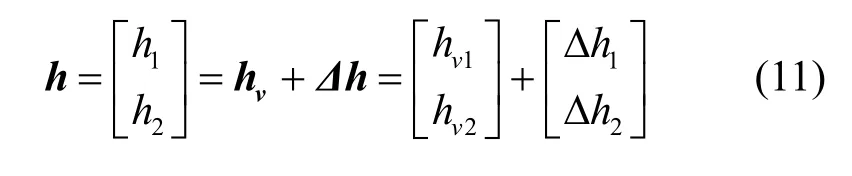
将式(11)代入式(3)，得到虚拟调制指数下CPM倾斜相位信号表达式如式(12)所示。

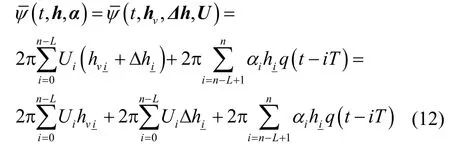
其中，最后一个等号右侧的第一项是虚拟调制指数所构成的相位状态项；第二项与调制指数增量Δh有关，称为虚拟调制指数的补偿项；第三项与传统的相关状态定义一致，不进行处理。

针对式(12)的第一项，可以定义新的相位状态转移关系如下。令虚拟相位状态为，从而相位状态满足递推关系如式(13)所示。

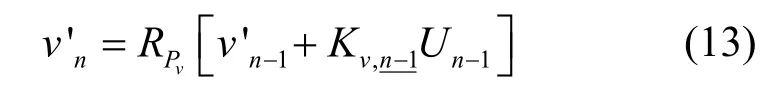
此时，VhD 的相位状态数为Pv。当Pv＜P时，与式(5)相比，式(13)定义的相位状态数更少了，总的网格状态数降低为PvML-1。基于VhD 的低复杂度检测算法步骤为：首先，将Pv取最小值；然后，按所有可能值遍历搜索式(10)中的分子项Kv1及Kv2，通过性能仿真结果获取最佳的虚拟调制指数集组合。

第二项可以参照文献[7-8]，利用PSP 的方法得到的n-L时刻前符号的估计值，再进一步计算补偿项。

将虚拟相位状态代入式(12)，可构造出基于VhD 的倾斜相位表达式如式(14)所示。

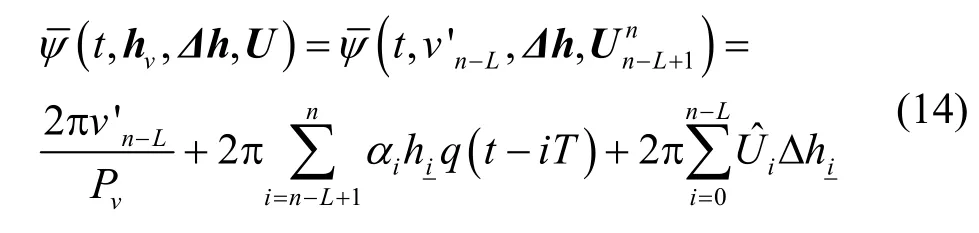
不同于文献[7-8]将虚拟调制指数融合进了相关状态中，本文仅将其置入相位状态中。由于VhD实际仅对相位状态有效，因此，式(14)的表达更加简明。

3.2 与频率脉冲截断算法的联合应用

虽然VhD 可有效简化相位状态，但其对状态向量中的相关状态并没有进行任何简化。因此，为了更彻底地降低网格状态数，可以将VhD 与其他能降低相关状态的算法联合使用。对于部分响应的Multi-hCPM 信号，FPT 算法[5]用于简化相关状态最为高效，该算法用于Multi-hCPM 的简化研究可参考文献[10-12]。

联合FPT 算法，并将式(14)代入式(2)，得到Multi-hCPM 信号基于VhD 和FPT 的简化相位表达式为

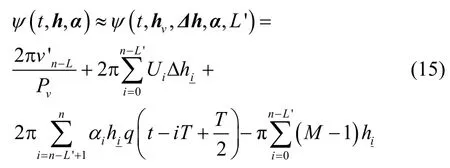
当FPT 的截断长度为L' 时，状态数将进一步降为PvML′-1，其中，截断长度L' ＜L。

4 仿真结果及分析

由于PSP 存在判决反馈的非线性过程，因此基于VhD 的简化算法难以采用理论推导来完成虚拟调制指数集的设计，故需要采用数值仿真来完成性能评估与VhD 简化方案设计。

针对Tier2 信号，采用Matlab 对本文提出的VhD算法进行蒙特卡罗仿真，并将信道建模为单边功率密度为N0的高斯白噪声（AWGN,additive white Gaussian noise）信道。仿真以最大信噪比=12 dB 或误比特率（BER,bit error rate）≤10-5作为停止条件，并统计误比特数超过200 或总符号数超过107。

4.1 VhD 的数值仿真结果

图1 为Pv=2 及Pv=3 的简化性能，图2 为Pv=4 的简化性能。图中“mst”表示状态数为m的简化方法。将MLSD 的误码曲线作为性能参照，下文的“性能损失”都是相对MLSD 而言的。值得指出的是，本文未给出Pv＞4 的简化方案的仿真结果，这是由于Pv越小，简化程度越高，同时Pv=4 的性能已经足够好（存在性能损失小于0.1 dB 的方案）。

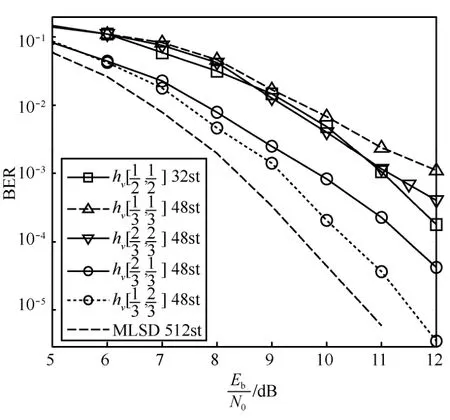
图1 Tier2 信号的VhD 误码性能（Pv=2 及Pv=3）

图2 Tier2 信号的VhD 误码性能（Pv=4）

表1 给出了图1 和图2 中所有方案在BER=10-5处相对于MLSD 的性能损失及复杂度对比。在仿真设置的最大信噪比（=12 dB）处，BER 未达到10-5的方案，采用该方案在=12 dB 处的BER 性能作为基准计算性能损失，并采用符号“＞”表示。

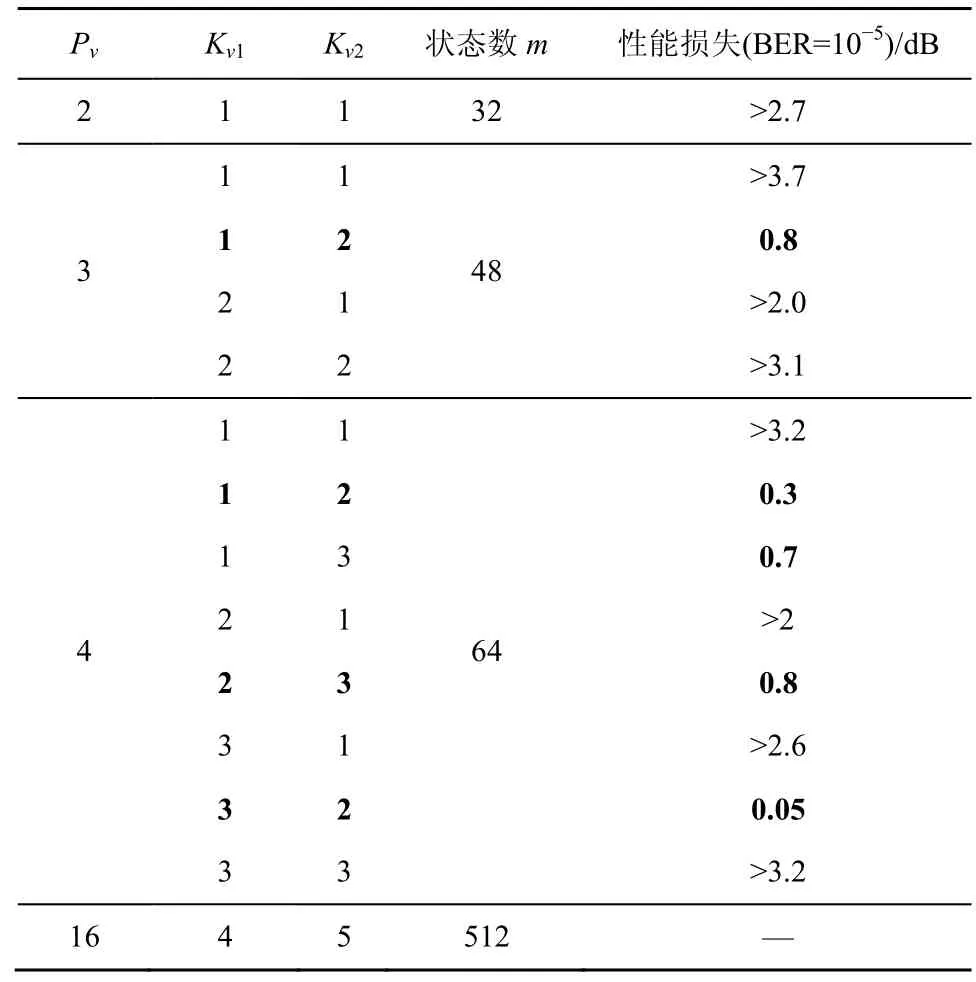
表1 VhD 的性能及复杂度对比

由仿真结果可以看出，当Pv=2 时，状态数简化到了32，但性能损失超过了2.7 dB；当Pv=3 时，状态数简化为48，其中，的性能最好，性能损失仅为0.8 dB，而的性能最差，超过了3.7 dB。

虽然Pv=4 的所有方案状态数都为64，但是性能却相差很大，其中，以的性能最佳，性能损失仅为0.05 dB，的性能损失为0.3 dB，的性能损失也都小于1 dB。相比之下，分别在≥10 dB和≥11 dB 区域出现了较大的误码率恶化，从而造成较大的性能损失。

值得指出的是，当hv1=hv2时，接收端可以退化为单指数CPM 的接收网格，但这些简化方案的性能并不理想。如图1 中的方案以及图2 中的性能损失都超过了2.7 dB。此外，虚拟调制指数集的元素位置也对性能影响很大，比如，前者性能损失仅为0.3 dB，而后者则大于2 dB。

由表1 的复杂度对比还可以看出，性能损失小于1 dB 的方案（表中加粗字体）中，状态数都不低于48，而性能损失小于0.5 dB 的方案中，状态数仍为64，因此需进一步结合FPT 作简化。

4.2 VhD 联合FPT 的数值仿真结果

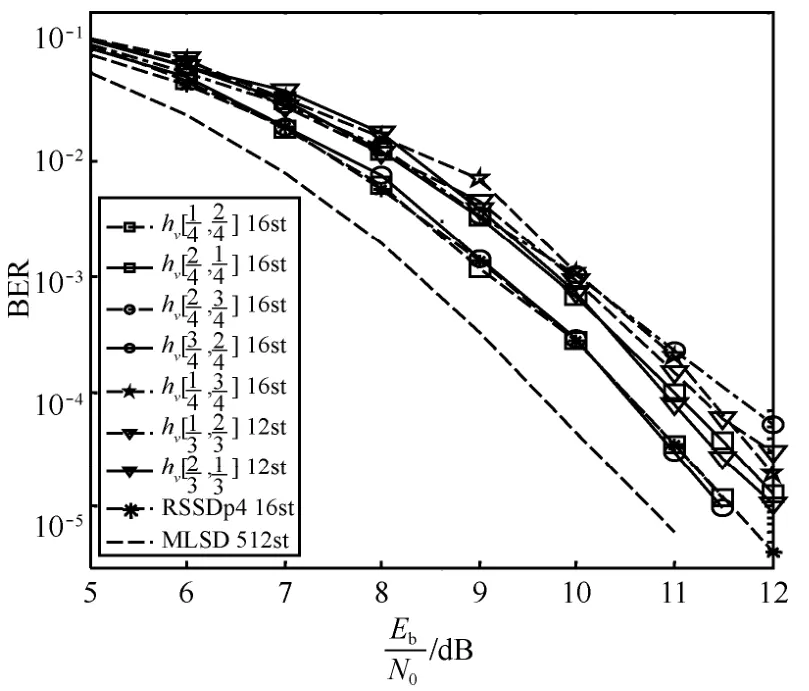
图3 Tier2 信号的VhD 联合FPT2 误码性能

将图3 中所有简化方案在BER=10-5处的性能损失列于表2。

表2 VhD 联合FPT2 的性能及复杂度对比

5 结束语

本文针对Multi-hCPM 信号，提出了基于虚拟调制指数集简化相位状态的低复杂度检测算法——VhD，并通过数值仿真完成了算法设计和性能验证。基于VhD 的低复杂度检测器在接收端构造虚拟调制指数集，通过控制虚拟调制指数的分母小于实际的调制指数分母，可有效降低相干序列检测的状态数。本文通过设计虚拟调制指数集的分母及调制指数集中元素的位置，构造了多组针对Multi-hCPM 的低复杂度检测方案。最后，将VhD 与频率脉冲截断算法（FPT）联合，更进一步降低了网格状态数。VhD 的算法设计以及与FPT 的联合算法都通过数值仿真进行了验证。由于Multi-hCPM 的多个调制指数周期出现，使VhD 比单指数CPM 的简化接收更加多元性。

数值仿真结果表明，针对Tier2 信号，当虚拟调制数集为时，检测状态数由MLSD 的512降低为64，而性能损失仅为0.05 dB。当与FPT 结合时，状态数可进一步降低至16 状态，而性能损失也仅为0.75 dB，检测复杂度和性能都优于文献[13]中FPT 与RSSD 联合的16 状态简化方案。