室内超密集网络中基于干扰图的自适应干扰协调方法

吴宣利，谢子怡，吴玮

（哈尔滨工业大学通信技术研究所，黑龙江 哈尔滨 150080）

1 引言

根据IMT-2020（5G）推进组预测，未来，5G系统将面临着数据流量千倍增长、千亿台设备连接和多样化的业务需求等多重严峻挑战，这实质上对未来通信系统的容量提出了更高的要求。而网络密度的增大被认为是提升无线系统容量的三大关键支柱之一[1]。超密集网络（UDN,ultra dense network）是异构网络密集化的结果[2]，UDN 通过密集化网络接入节点获得更高的网络密度，同时获得更高的频谱复用效率，从而在局部热点区域实现百倍量级的系统容量提升。

在超密集网络中，除宏基站（MBS,macro base station）外，包含大量的低功率接入节点，这些低功率接入节点被称为小小区基站（SBS,small cell base station），简称小小区。小小区被认为具有低功率、低成本、接入简单、即插即用等特点[3]，其部署能够有效提高基站在高用户密度区域的覆盖。

然而，超密集网络系统也面临着诸多问题和挑战，干扰管理便是其中之一。随着，接入节点部署密集化程度和频谱复用频率的提高，干扰变得严重而复杂：接入节点之间距离的缩短使小区间干扰强度增大；低功率接入节点的引入在原有同层干扰的基础上带来了跨层干扰；接入节点部署位置的随机性使干扰的分布更加难以预测[4]。严重的干扰将大大降低网络密集化带来的系统容量的增益，寻找有效抑制干扰的方案就变得十分重要。

此外，考虑到办公室、公寓、密集住宅区等热点地区多为室内场景，而现有文献对室内场景下的超密集网络系统研究较少，本文将针对室内场景的超密集网络进行研究，并提出一种半集中式的干扰协调方法，该方法能够根据系统内接入节点和用户的分布自适应调整资源分配方案。

2 相关工作

文献[3]指出，超密集网络架构中的干扰本质仍为同频干扰，因而频率资源的复用是产生干扰的根本原因。干扰协调和资源分配策略在密度较低、干扰较小的蜂窝网络中已经得到了充分的研究[5-7]。文献[5]对部分频率复用、软频复用等小区间干扰协调技术进行归类和研究，这些技术通过频率资源的复用有效地缓解了同构网络中宏蜂窝间的干扰。文献[6]采用几乎空白子帧（ABS,almost blank subframe），在时域上将资源分为两部分以降低小小区用户间的干扰。文献[7]提出了一种降低功率几乎空白子帧的小区间联合干扰协调算法，通过功率控制在充分利用时域资源的同时降低干扰。然而，这些技术不能解决小小区密集部署时的强干扰。

鉴于需要对系统中小小区间的干扰情况进行考虑，图论中的干扰图被广泛应用于超密集网络系统的干扰协调算法中[8-10]。超密集网络系统中的小小区可建模为图的顶点，小小区间的干扰关系建模为图的边，由此建立系统的干扰图，而资源分配的过程即是对各顶点进行着色的过程。在文献[8]中，当干扰信号与有用信号的参考信号接收功率（RSRP,reference signal received power）的差值大于预定门限值时，就认为2 个小小区间存在干扰，2 个小小区所代表的顶点用一条无向边连接。由于无向干扰图难以准确描述干扰关系，文献[9-10]采用了加权有向干扰图对系统进行刻画。文献[9]用小小区在一个物理资源块（PRB,physical resource block）上受到的干扰功率大小作为这条有向边的权重值，该干扰值在计算时仅考虑了小小区之间的距离而未考虑用户到小小区的实际距离。文献[10]则将受到干扰最强的用户的干扰功率值作为小小区间有向边的权重值。

在建立系统的干扰图后，需要对顶点进行着色以实现频率资源的合理复用。图的着色问题通常为NP-hard 问题，即在多项式时间内无法求得最优解。文献[11]采用一种穷举搜索方案对无向图进行着色。文献[12]首先根据干扰图将用户进行分簇以降低运算规模，然后利用图的匹配算法进行资源分配。文献[11]和文献[12]的算法虽然能求取最优的资源复用策略，但是这些算法本质即为穷举所有可能情况，不适用于小小区密集部署的情形。通常可以采用启发式的着色方法以获得次优分配方案[9,13]。文献[13]提出了一种基于贪婪算法的信道分配策略，该算法有效抑制了顶点间的强干扰。文献[9]提出了一种迭代着色算法，该算法充分考虑了系统内的所有干扰，并通过多次迭代使分配结果进一步逼近最优。

现有研究成果虽然在一定程度上缓解了系统中的强干扰，但是仍旧存在以下不足：1)由于模型的限制，现有文献建立的干扰图往往难以反映室内场景下系统内实际的干扰情况；2)现有文献考虑场景中的用户和小小区的密度均偏低，而随着对超密集网络的网络容量的提升，用户密度和小小区密度均将大幅度提升。针对上述不足，本文针对超密集网络室内场景提出了一种基于干扰图的自适应干扰协调方法，该方法首先建立一种能够较为准确地反映系统中干扰情况的干扰图，然后根据建立的干扰图采用启发式算法进行资源分配，从而实现有效的干扰协调。所提方法在用户和小小区密度均较高时，仍然能够根据信道状况、接入节点、用户位置分布等因素的改变所引起系统干扰关系的变化自适应地实现资源的合理分配。

3 系统模型

本文参考了3GPP 定义的dual-stripe 模型[14]对超密集网络的室内场景进行建模。如图1 所示，两栋单层建筑位于一条10 m 宽的露天街道两侧，每栋建筑均含有两排房间，图中每个方格代表一个10 m×10 m 的房间。小小区基站在各个房间内呈随机均匀分布，各房间内有且仅有一个小小区。为了便于对模型进行分析，本文仅考虑位于室内区域的用户。现有文献通常采用泊松点分布来模拟用户随机分布的状态[15-17]，因而本文考虑用户在室内区域呈泊松点分布，由室内的小小区提供覆盖。用户根据RSRP 值的大小选择最佳的小小区进行接入，一个用户仅接入一个小小区，无接入用户的小小区将被关闭。图1 中用户和小小区均采用一根天线进行传输，且天线类型为全向天线。本文认为宏基站和小小区工作在不同频段。

图1 超密集网络室内场景

本文采用文献[14]定义的路径传输损耗模型。相对于室外模型而言，墙壁的穿透损耗和室内传播距离等因素均会对室内模型的路径传输损耗大小产生影响。此外，本文综合考虑了阴影衰落和小尺度衰落，将阴影衰落的标准差设置为10 dB，小尺度衰落采用块衰落和国际电信联盟（ITU，international Telecommunication Union）提出的ITU InH（indoor hotspot）模型[14]，并假设小小区可以获得所有信道的准确信道状态信息。同时，本文参考了OFDMA（orthogonal frequency division multiple access）系统中的资源分配模型，将物理资源块，即PRB 作为资源分配的最小单位。

考虑下行场景，Ntot={1,2,…,N}表示小小区的集合，记小小区n（n=1,2,…,N）覆盖范围内的服务用户集合为Γn，该覆盖范围内的用户数Mn=|Γn|，其中，|·|表示基数。则系统内用户总数为表示第i个用户与小小区n相连接。由于无连接用户的小小区将被关闭，这些小小区对系统不产生影响，因此不包含在集合Ntot中。系统中可用的PRB集合记为Ω={1,2,...,K}，矩阵A={aik|aik∈{0,1}}表示PRB 的分配结果，当第k个PRB 分配给用户i时aik=1，否则aik=0，则第i个用户在第k个PRB上的信干噪比可表示为

其中，σ2为白噪声功率，为小小区n到用户i在第k个PRB 上的信道增益，包含了天线增益、路径传输损耗、穿透损耗、阴影衰落和小尺度衰落；集合表示功率分配的结果，为小小区n对第k个PRB 分配的发射功率。为了简单起见，本文中所有的速率均由香农容量来表示。事实上，基于相应的接收机算法及调制编码方案能够根据接收信号的SINR 计算出实际的速率大小，则用户在第k个PRB 上获得的传输速率为

其中，W为PRB 的带宽。

4 问题描述

由于超密集网络本身是为了提升系统的容量，本文以最大化系统吞吐量为目标函数，则该问题可规划为一个非线性混合整数规划问题，即问题的目标函数及限制条件可以写为

其中，Pmax为小小区的最大发射功率。约束条件C1表示各小小区内用户使用正交的资源块，即各小小区内PRB 不复用；约束条件C2表示小小区对各PRB 分配的功率值非负；约束条件C3表示小小区对各PRB分配的功率之和不大于小小区的最大发射功率。本文假设对一个用户仅分配一个PRB，功率分配采用平均功率分配。

显然，目标函数为非凸的，则该非凸混合整数规划问题是NP-hard 问题，即在多项式时间内无法求解。本文将原问题分解为三部分，提出一种分层半集中式的方法进行求解，具体如下：1)将系统中的干扰关系建模为加权有向干扰图；2)根据干扰图采用迭代着色算法决定各小小区的可用频率资源；3)小小区采用优化吞吐量的资源分配算法分别对其连接用户进行资源分配。在第一部分和第二部分中，先以一种集中式的方法基于干扰图对系统进行干扰协调，充分考虑网络各部分特征从而有益于系统性能的进一步提升；第三部分则采用分布式手段，相对于集中式方法而言能有效降低计算复杂度[18]。

5 自适应的干扰协调方法

5.1 干扰图的建立

记室内超密集网络系统建模的干扰图为G={Ntot,E}，由于休眠小小区对系统内用户的影响可不计，干扰图的顶点Ntot为系统内所有的活跃小小区，干扰图的边E为这些小小区间的干扰关系。如何有效提取系统中的干扰关系，并据此建立干扰图的边是干扰图建立的关键，直接影响到后续算法的选取和系统的性能。

目前，很多文献在建立干扰图时，均将系统建模为无向图，且采用预定的门限值来对干扰进行判定，例如文献[8]中所述。虽然这种干扰图建立算法简单且信令开销很小，但是生成的干扰图只能非常粗略地描述系统中的干扰情况，这将影响后续的频率资源的分配结果，从而影响系统性能。此外，大多数情况下，随着网络拓扑结构的变化，取得最佳系统性能时的干扰门限值也会有所改变，难以保证系统性能最优，即对网络拓扑结构变化的稳健性较差。

为了较为准确地对系统中的干扰情况进行描述，本文将室内超密集网络系统建模为一个加权有向干扰图。图2 为一个包含3 个小小区和4 个用户的网络系统构建有向干扰图的例子，粗实线表示用户与小小区的接入关系，其他3 种线型在网络系统中表示小小区对非接入用户的下行干扰，箭头表示提取出的干扰关系。

图2 超密集网络系统干扰图构建例子

对于小小区m和n，Mm和Mn分别表示与它们相连接的用户总数。小小区m对小小区n的干扰emn表示为

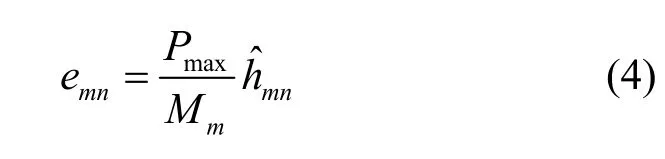
其中，hmi为小小区m到用户i的平均信道增益。在该干扰图中，干扰边权重的物理意义为小小区m在一个PRB 上对小小区n产生的干扰功率，干扰边方向的物理意义即为干扰的指向。当m=n时，emn=0，即该干扰图关联矩阵的对角线元素均取0。实际中，由于距离较远及穿透损耗的影响，用户难以感知到来自部分小小区的参考信号，此时可直接认为干扰的功率值为0，即这条有向边不存在。

5.2 干扰图的迭代着色

在建立系统干扰图之后，需要根据干扰图对各小小区可使用的频率资源进行分配。通常将系统中的频率资源建模为不同的颜色，对超密集网络系统的干扰图进行着色处理。本文采用集中式的方式直接对各小小区的可用资源进行分配，而不再对小小区进行分簇，主要有以下2 点原因：1)虽然室内场景的超密集网络相对于室外场景密集程度更大，但是由于小小区位置分布受房间分布的限制，相邻房间的小小区间的干扰关系较为一致，而随着穿墙面数及距离的增加相隔越多房间的小小区间干扰关系越微弱，现有的分簇算法很难将该系统内的小小区分成大小适中的簇；2)实际场景中，虽然用户及小小区密度能达到室外场景的近百倍，但是单层房屋内房间数量最多为几十个，则室内场景的超密集网络中小小区数目不会过于庞大，进行全局优化的实现复杂度及信令开销不会太大。

本文所采用的迭代着色算法是在文献[9]提出的迭代着色算法基础上进行的改进。本文的启发式迭代着色算法以最大化系统和速率为目标，对前文建立的加权有向干扰图进行着色，能够根据网络拓扑结构、用户密度及信道状况自适应地调整各小小区的可用频率资源。

在迭代着色过程中，记集合V为干扰图中待着色顶点的集合。构建N×K维矩阵S和C，其中，S={snk|snk={0,1}}为PRB 在小小区的分配关系矩阵，snk=1 时表示第k个PRB 分配给了小小区n，snk=0为第k个PRB 未分配给小小区n；C为代价矩阵，其元素cnk表示第k个PRB 分配给小小区n时该小小区所需付出的代价，即在小小区n使用第k个PRB 所受到的干扰。cnk可以表示为

其中，emn为小小区m对小小区n的干扰，其表达式如式(4)所示。

加权有向干扰图的迭代着色算法描述如下。

步骤1初始化。已知活跃小小区的总数为N，令V=Ntot={1,2,...,N}，并令矩阵S和C均为零矩阵。

步骤2对顶点进行排序。对其他小小区造成干扰严重的小小区将具有更高的优先级，采用从小小区n出发的边的权重和来衡量小小区n对其他小小区的干扰程度In，如式(7)所示。

In越大，优先级越高。若同时存在多个边的权重和相等的小小区，则所需PRB 较多的小小区，即具有较大用户数Mn的小小区具有更高的优先级。

步骤3选择着色顶点。V中具有最高优先级的小小区n'将被最先着色。

步骤4选取具有最大回报的PRB 对选定顶点进行着色。当某个PRB 分配给选定的小小区时，将系统能够获得的总速率称为该PRB 带来的回报，记为Q。Q的定义如下，当第k个PRB 分配给小小区n'时，回报值Qk为

其中，

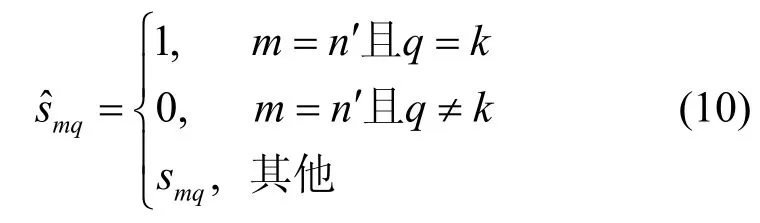
步骤5在小小区n'着色完毕后，更新矩阵S中相应的元素值，并根据矩阵S及式(6)更新矩阵C，删除集合V中的顶点n'。

步骤6检查V是否为空。若V不为空，则返回步骤3，继续寻找顶点进行着色，如此循环，直至所有顶点均被着色；否则进入步骤7。

步骤7为了保证分配结果的准确性及最优性，多次迭代求取最终的分配结果，要求在一定的迭代次数内迭代达到收敛。第p次迭代后系统所能获得的总速率Rp可表示为

步骤8根据矩阵S向各小小区报告可以使用的频率的资源，以便完成PRB 在各小小区的分配。

相对于文献[9]提出的迭代着色算法，本文采用的迭代着色算法优化了计算步骤，且修正了步骤4 中Qk的计算式，保证了分配过程中不同PRB 间的公平性。

5.3 资源分配

5.2 节迭代着色算法仅决定了各小小区的可用PRB 资源，各小小区还需要对其连接用户进行资源分配。此时，若采用平均功率分配，对于每一个小小区n，式(3)所示的问题可简化为

其中，Ψn为小小区n的可用PRB 的集合。

然而，该问题的目标函数依然为非凸函数，且限制条件为二值整数，难以通过优化算法求解该问题最优解的闭合表达式。当小小区中用户数量较多时，采用穷举进行求解是不实际的，因此，需要考虑一个复杂度适中的算法进行求解。

考虑到资源分配的目标是最大化各小小区的吞吐量以最大化系统吞吐量，可以采用一种优化吞吐量的资源分配方案，该方案按照一定优先级顺序对用户分配资源，在每一次资源分配中均保证被分配资源的用户获得的速率达到最大。对于小小区n，该优化吞吐量的资源分配算法描述如下。

步骤1初始化。令待分配用户集合Un为与小小区n连接的Mn个用户的集合。可分配PRB 集合Ωn=Ψn。

步骤2对用户进行排序。计算各用户的平均信道增益，如式(14)所示。

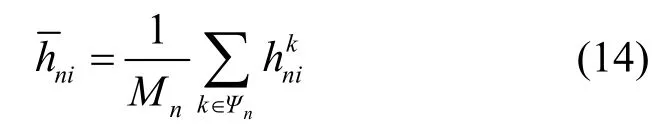
然后，根据计算得到的平均信道增益由大到小对Mn个用户进行排序。平均信道增益越大，用户优先级越高。

步骤3选择待分配用户。在待分配用户集合Un中选取具有最高优先级的用户i'对其分配PRB，如式(15)所示。

步骤4选择PRB 分配给步骤3 中已选择的待分配用户。选择标准是选取Ωn中能使该用户获得最大传输速率的第k'个PRB，如式(16)和式(17)所示。

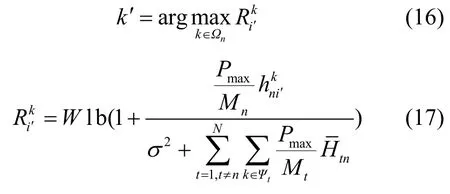
步骤5判断集合Ωn是否为空，即该小小区所有可用的PRB 是否全部分配完毕，若没有，则返回步骤3；否则结束分配。

6 数值分析

本文采用Matlab 对提出的室内场景超密集网络中基于干扰图的自适应干扰协调方法进行仿真分析，仿真区域如图1 所示。图1 中100 m×70 m的区域内共有100 个用户，即密度为0.14 人每平方米。由于办公室、公寓等超密集网络室内场景中的用户主要处于相对静止的状态[1]，本文未考虑用户的移动性。实验的仿真参数如表1 所示。此外，路径传输损耗、穿透损耗及小尺度衰落均采用3GPP相应协议定义的参数[14]。

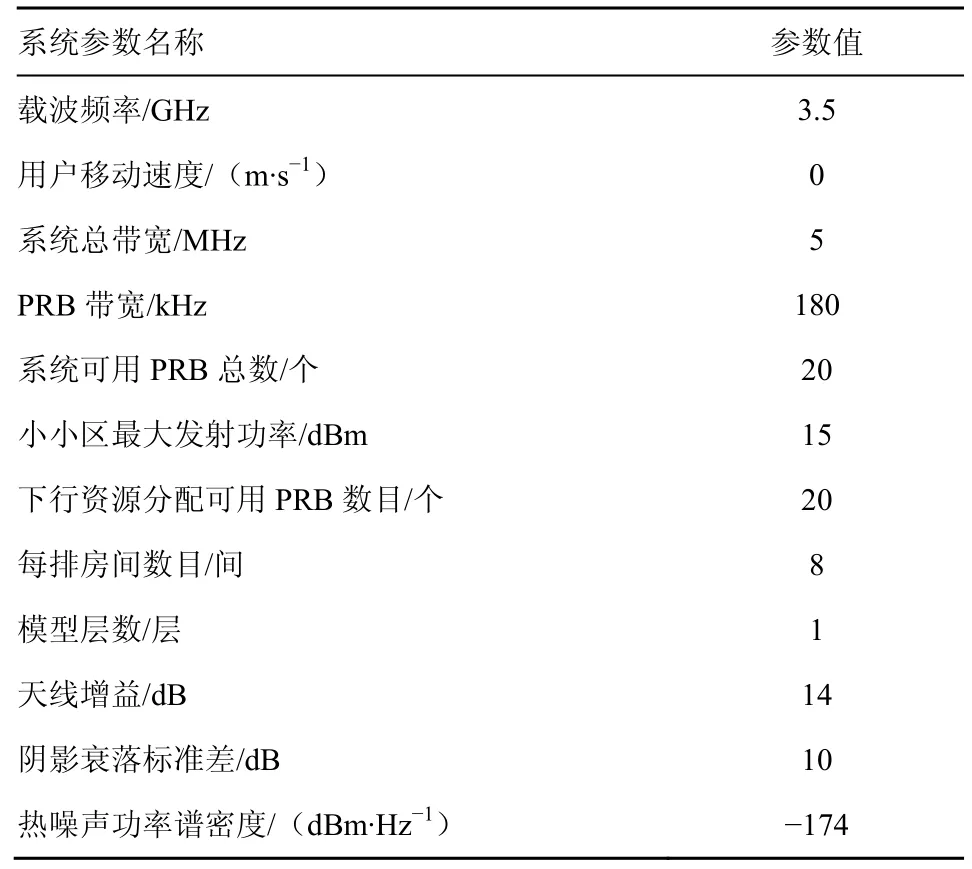
表1 室内超密集网系统仿真参数

除了本文提出的方法外，本文对文献[8]、文献[9]及传统的轮询算法进行仿真，作为对比方法。其中文献[8]和文献[9]均为基于图论的干扰协调算法，文献[8]采用传统的0-1 干扰图进行干扰协调，文献[9]则给出了一种自适应的干扰协调算法。而轮询算法是最简单、基础的经典调度算法，这种不考虑瞬时信道条件而使用户轮流使用共享资源的调度策略能保证用户之间较好的公平性，且轮询算法在超密集网络中与比例公平算法性能差距不大，考虑其简单性更适用于超密集网络[19]。图4 和图5 中文献[9]的方法用基于有向图的自适应干扰协调表示，文献[8]的算法用基于无向图的干扰协调表示。

6.1 迭代着色算法的收敛性

在本文中，最大化系统和速率与最大化系统吞吐量的目标是一致的。在对迭代着色算法的收敛性进行分析时，考虑迭代次数与系统和速率的关系。当系统中用户总数分别为80、120 和160 时，干扰图的迭代着色算法的收敛性如图3 所示，仿真结果显示了随迭代次数增加，系统速率的变化情况。

由图3 可知，系统速率随着迭代次数的增加逐渐增大，在10 次迭代内趋于平稳。事实上，本文采用的迭代着色算法本质上为一种贪婪算法，任意2 次着色过程之间是相互独立的，且每个顶点在着色时均以最大化系统和速率为目标，因此，着色顺序靠后的顶点在着色时均选择对已经着色的顶点影响最小的PRB 进行着色。迭代过程中同理，每次迭代都是基于上次迭代的结果选择最佳的PRB 进行着色，直至达到最优。

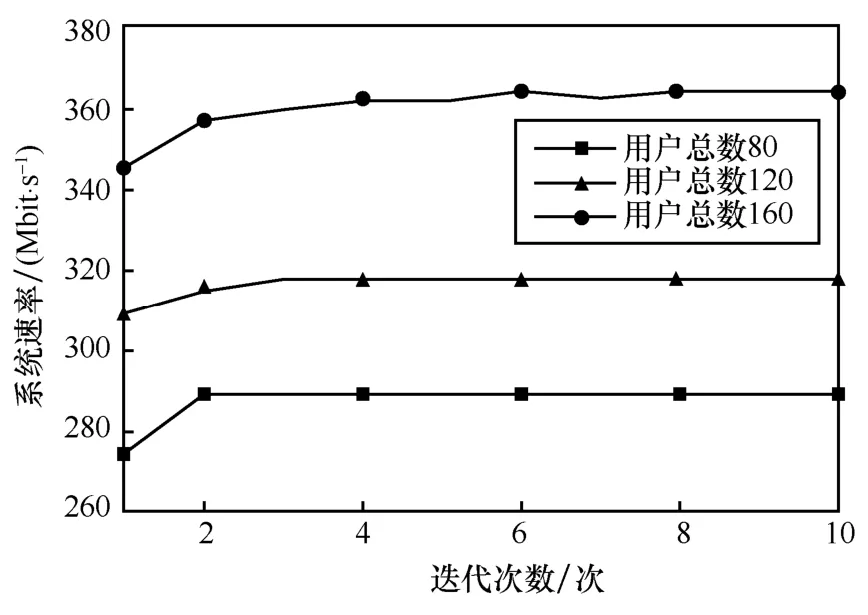
图3 迭代着色算法的收敛性

6.2 系统吞吐量与中断概率

当系统内用户数目从0 增加到200 时，本文所提方法及对比方法所能获得的吞吐量性能如图4所示。

图4 不同干扰协调方法的系统吞吐量

由图4 可知，本文所提方法始终具有最优的性能，且当用户数大于80 时，相对于次优的文献[9]算法具有10%以上的性能增益，这是因为当系统内用户很少时，由于资源相对充裕，用户间干扰较弱，各算法性能差异较小；而随着系统内用户数目逐渐增多，系统内干扰愈加严重，本文所提方法能够有效进行干扰协调从而获得吞吐量的增益；若用户数目持续增加，由于系统内资源有限，各方法获得的系统吞吐量将趋近于系统容量上限，这表明本文所提方法能够较为精确地获得系统内的干扰情况，并能根据干扰情况自适应地调整资源分配策略。

图5 显示了系统内用户数不同时本文所提方法及对比方法的中断概率。对于相同的用户数和用户速率需求，本文提出的方法始终具有最低的中断概率。这在一定程度上表明本文提出的方法获得的吞吐量增益并不是牺牲用户之间的公平性得到的，而是通过资源分配策略有效协调干扰，提升各用户接收信号的信干噪比，从而提升各用户的吞吐量。在用户数相对较低、系统内干扰相对较弱时，用户实际获得的速率更高，在相同坐标下本文提出的方法的性能优势更加明显。

6.3 复杂度与信令开销

通过上文的分析可以发现，本文所提基于干扰图的自适应干扰协调方法和基于有向图的自适应干扰协调的性能明显优于另外2 种对比方法，因此本节从算法复杂度以及信令开销的角度对这2 种方法进行对比。

由于时间复杂度主要是由循环迭代次数决定的，迭代着色算法的时间复杂度决定了整体的时间复杂度，通过计算可以发现2 种方法的时间复杂度均为O(KN2)。

由图4 可以发现，本文所提方法相对于基于有向图的自适应干扰协调而言，在系统中用户总数大于90 时，能获得至少40 Mbit/s 的系统吞吐量增益。考虑最坏的情况，系统内全部的32 个小小区均处于活跃状态，且所有的小小区均有31 个相邻小小区，平均每个小小区连接6 个用户。假设上报时间的间隔为100 ms，则对于本文所提方法而言，每次上报时平均每个小小区信令开销为4×31×6=744 bit，此时平均每个小小区内吞吐量提升了1.25×106bit/s，而对于基于有向图的自适应干扰协调而言平均每个小小区信令开销为4×31=124 bit。本文所提方法获得的吞吐量增益可达到额外信令开销的近千倍，提出方法的额外信令开销相对于获得的吞吐量增益而言可忽略不计。考虑系统中用户总数较少的情况，虽然系统吞吐量增益降低，由于小小区内用户数减少，此时额外的信令开销也相应的降低，虽然额外信令开销相对于吞吐量增益难以完全忽略，但系统中断概率明显降低，所提方法仍具备一定的优势。

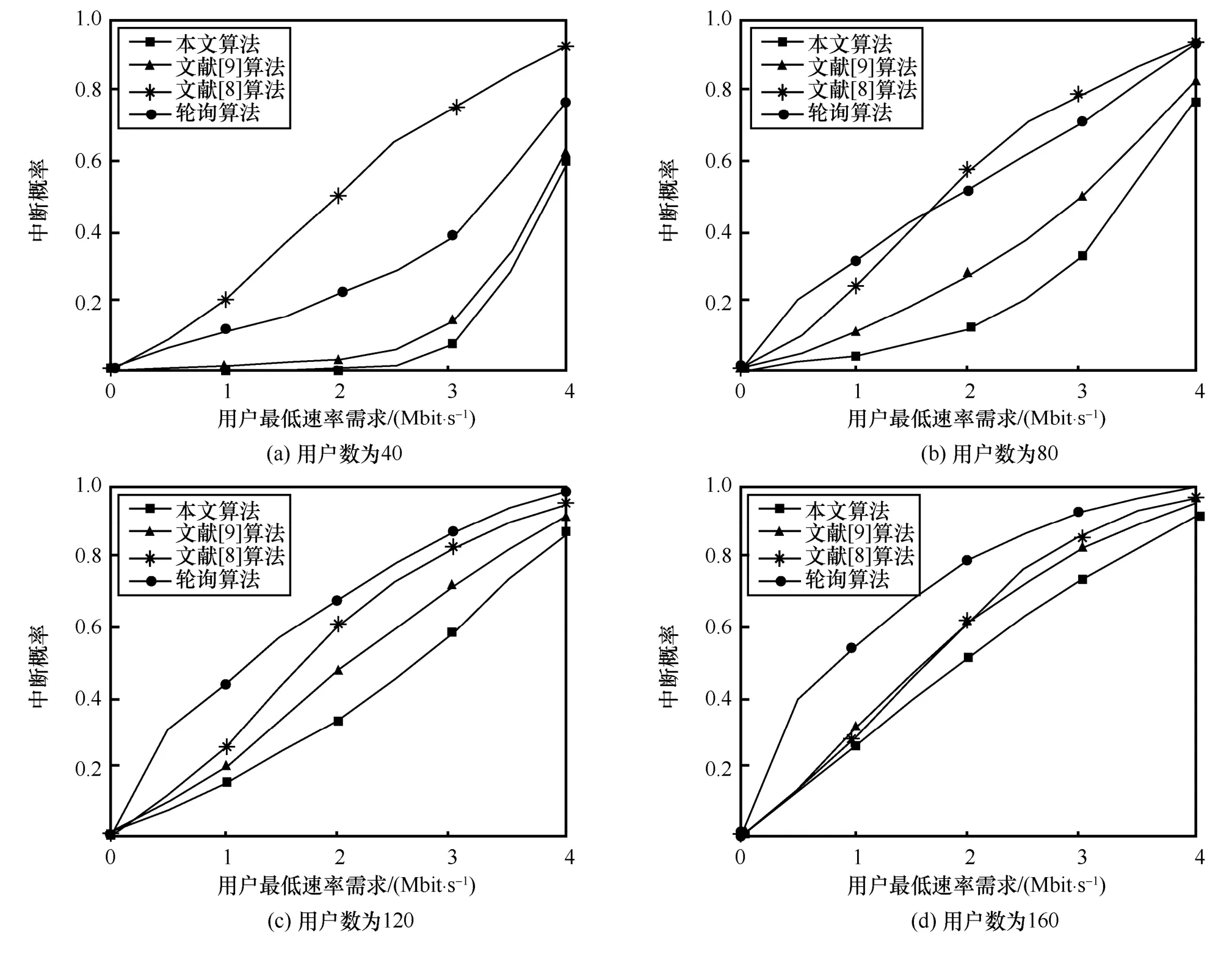
图5 系统中用户总数不同时的系统中断概率

7 结束语

本文以最大化系统吞吐量为目标，研究了室内超密集网络场景下的干扰协调问题，将系统内的干扰关系建模为加权有向干扰图，采用一种分层半集中式的方法根据干扰图自适应地进行资源分配。仿真结果表明，所提方法在未提升算法复杂度的前提下有效地提升了系统的吞吐量，降低了用户的中断概率，当系统内用户数为80～200时，即干扰较为强烈时，所提方法可以获得至少10%的系统吞吐量增益，与此同时能有效降低中断概率。

在下一步工作中，需要结合用户的业务需求对更加优化的功率分配算法进行研究，在进一步优化系统吞吐量性能的同时使优化问题的限制条件更加符合实际情形。