长租公寓节能改造决策分析

李昇翰,郑宏业

（深圳大学土木工程学院）

1 引言

近年来，房地产行业的快速发展，我国建筑面积急剧增长，但随之也面临巨大的能源消耗问题。据前瞻产业研究院发布的中国智能建筑分析报告显示，截至2017年，在我国260亿㎡的城镇住宅中，高能耗建筑占比超过90%，而我国城镇节能建筑仅占既有建筑面积的23.1%左右[1]。在建筑物的长寿命周期中，包括暖通空调，照明，设备和电器等在内的运营能源服务占建筑总能耗的约80%[2]。

由于既有建筑大多没有采取任何的节能措施，其建筑的外围护结构热工性能差，窗户的气密性不足、且传热系数极高等等，导致采暖制冷等用能效果极差、能源消耗非常大。因此提高现有建筑的能效无疑被认为是减少碳排放和能源消耗的最可持续和可行的措施之一[3]。

由于市场的发展以及国家政策的推动，“长租公寓”以新建和改造两种方式逐渐的走向历史发展的大舞台，在大量的既有建筑改造过程中，通过改造翻新，建立新的租住单元，从而打造全新的生活和社交空间，引领当前租赁行业社区化新发展[4]。

然而，长租公寓的建筑改造虽然优化了空间设计，提高了空间使用效率[4]，但忽略了老旧小区能耗大、资源消耗水平高这一重大问题，因此从社会环境、资源状况的角度来看，长租公寓的发展并不能说是恰到好处。所以，立足当前社会、经济、环境形势，若能在改善老旧小区居住环境较差、设备陈旧、结构老化等问题的同时，使用绿色节能的手段对其进行更深一步的改造，那么将有效的降低建筑能耗，改善居住环境，提高舒适度，使长租公寓提升到一个更好的运营状态[5]。

但是，既有建筑的绿色改造虽然可以提升能源使用效率，降低能耗，但也在一定程度上增加了开发商的投资成本，这是投资商想极力避免的。所以，提出一个基于成本和效益的“盈亏平衡分析”模型，便于投资商结合自身情况选择适合的改造方案。首先设定相关改造指标，建立层级结构；然后通过专家打分法为各指标打分，并用层次分析法计算指标权重；接着通过“盈亏平衡分析”模型生成多种组合方案，运用比值分析计算各方案的增量成本与增量经济效益比重；最终将得出三个备选方案，由投资商自行选择。

2 长租公寓节能改造

查阅文献可知，国内并没有太多针对长租公寓节能改造的案例，但根据《既有居住建筑节能改造指南》[6]、《既有居住建筑节能改造规程》[7]以及《夏热冬冷地区既有居住建筑节能改造工作补助资金管理暂行办法》等文件来看，不仅给建筑节能改造质量保证措施提供了建议，而且从技术方面对节能改造进行了规范和指导[1]。

由于研究重点在于决策体系的构建，因而不必对具体改造方案进行论述。参照《公共建筑节能改造技术规范》的建议，建筑节能改造的静态投资回收期应小于等于8a[8]，且通过走访调查现有长租公寓翻新案例，仅从以下7个地方进行研究，并用于模型的建立，具体为：外立面改造、外遮阳改造、内遮阳改造、窗户改造、照明改造、太阳能设备采用以及绿色节能屋顶改造，其详细改造方案（见表1）。

3 理论及模型

3.1 层次分析法确定改造方案权重值

层次分析法（The analytic hierarchy process）简称AHP，由托马斯·塞蒂（T.L.saaty）在20世纪70年代中期提出，其结合定性与定量两种分析方法，实现对问题的系统性、层次性分析，加之处理复杂问题的便捷性、直观性，使其在社会许多方面得到广泛应用[9]。

3.1.1 建立层次结构模型

首先以成本为例作为目标层，相关七个改造措施作为准则层，对应改造措施的改造方案作为方案层，建立如下层次结构模型（见图1）：

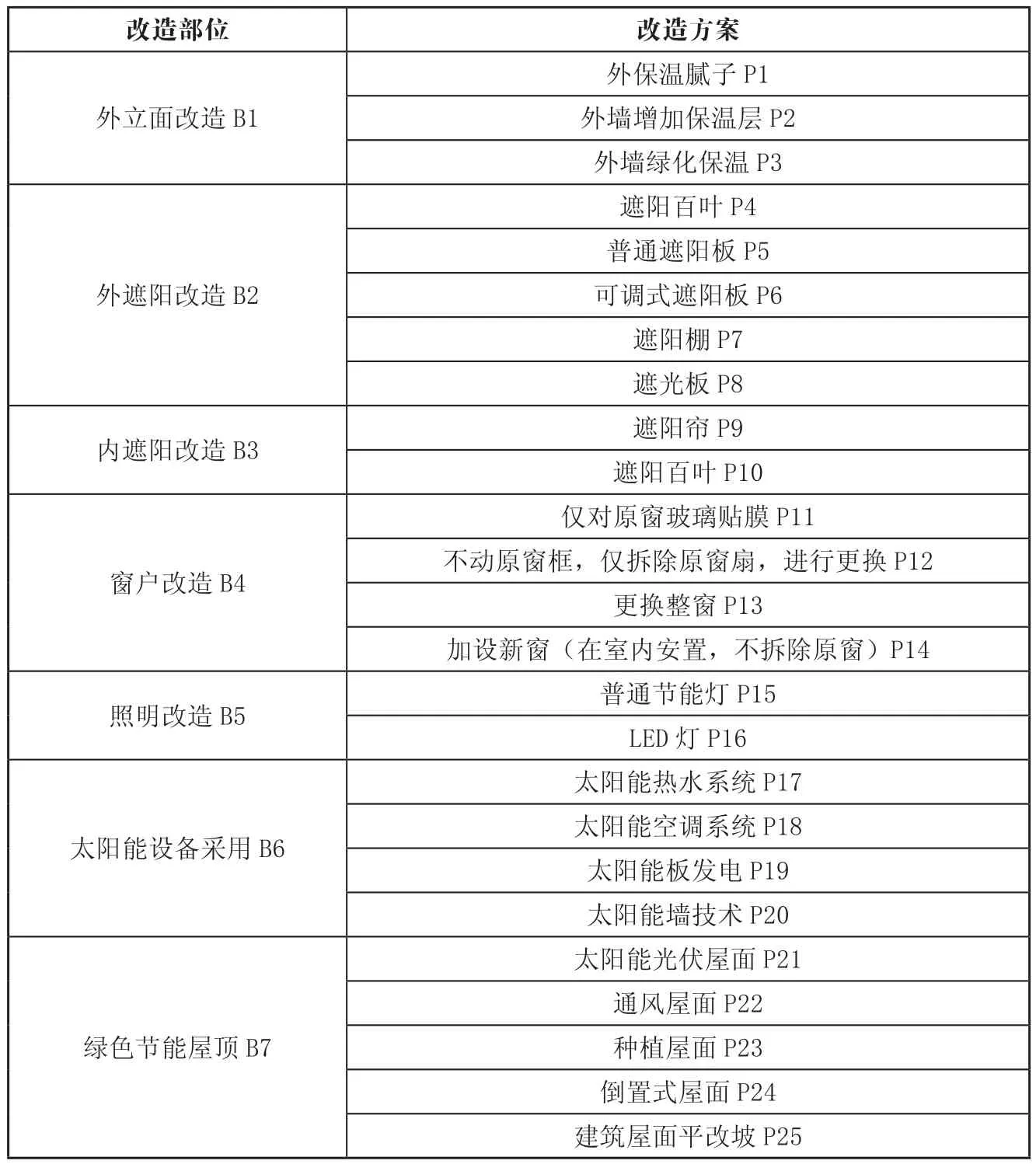
表1 长租公寓翻新改造指标体系

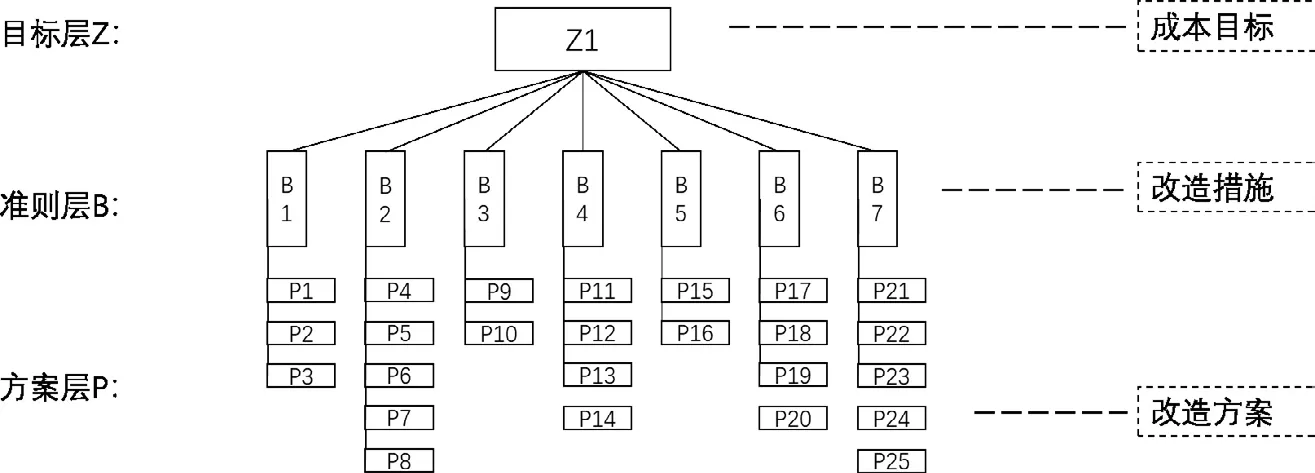
图1 7个改造措施的层次结构

3.1.2 构造判断矩阵

根据层次结构模型，构造判断矩阵（见表3，仅以准则层为例），然后由专家以及利益相关者根据矩阵判断标度（1～9标度法，见表2）进行打分，本文将用aij代表专家给与的分数（见表3）。

其中，aij＞0，aii=1；

3.1.3 计算各改造方案权重值

根据表 3 设矩阵 A=（aij）n×n，利用公式①可计算矩阵特征向量，并在最终得出方案层所有改造方案的权重值：

式中，ω为特征向量，λ为特征值。这里规定25个方案的权重值用ω1，ω2，ω3，……，ω24，ω25代替，简记为 {ω=ωi|1≤ i ≤ 25}。

3.1.4 一次性检验

为了使对应特征根的特征向量能代表权向量，需对其进行一致性检验，一次性检验通过计算CR来确定，当得出的CR＜0.1时，则认为一致性检验通过，否则，为不通过。

式中，n为矩阵的阶数，λ为特征值，RI根据下表4进行确定：

3.2 Python实现多方案组合

Python是一种简便灵活的脚本语言，由于其便捷的特点在系统开发、科学计算等领域广泛使用[10]。因而可在python环境中利用数组的排列组合方法实现方案的互相组合。

如：记列表list=[1,2,3]，可使用for循环遍历list中的元素，然后返回到新的列表中,从而得到[1]，[1，2]，[2，3]，[1，2，3]，同理可实现对表2改造方案的随机组合，但由于改造方案中仅对原窗贴膜和整窗更换不能兼容，所以应该对方案的组合进行条件限制，可用Pi表示方案i的选用，Pi=1,则记为选用，Pi=0记为不选用，然后令≤1即可实现上述条件限制。

3.3 模型建立

盈亏平衡分析是通过盈亏平衡点分析项目成本与经济收益的平衡关系的一种方法，通过各种不确定因素的变化带来的经济后果，找出某一因素影响方案选择的临界值，即盈亏平衡点，根据不确定因素的变化对投资方案影响程度进行决策分析[11]。

传统的盈亏平衡分析法通过寻找效益与成本的平衡点来判断不确定因素的变化对投资的影响情况，本文则利用比值法，即通过长租公寓节能改造的增量成本与其带来的增量效益的比值来反映节能改造的收益情况，公式如下：

结合以上分析可得模型：

式中：ω（i效益）为以节能改造的经济效益做为目标层计算的权重值，同理ωi（成本）是以节能改造的增量成本作为目标层计算的权重值；Bi为某一个节能改造方案的单位面积增量成本；ei为某一个节能改造方案的单位面积增量经济效益；pi=1则表示选择该项方案，否则不选。

表2 利益相关矩阵判断标度

表3 准则层判断矩阵

表4 RImn阶数征值表

4 结语

根据以上模型可以知道，当增量效益大，增量成本小的时候，F值越大，反之F值越小；F值越大则代表方案较优，因而可提取F值排列前三的方案供投资商选择。

该模型的优点在于可以为开发商提供直观的成本效益比重，为其在前期的改造决策提供了重要的借鉴意义；不仅如此，在今后的普通住宅以及办公楼的节能改造分析中，亦可使用本模型进行成本效益的分析；然而遗憾的是，本文没有具体的给出相应的节能改造投资回收期，因为相对于长租公寓的改造，投资商对公寓楼并没有持有权，所以相应的节能改造投资回收期也是决策的重要一部分。