煤与瓦斯突出区域预测瓦斯地质方法的可靠性预计

2019-09-27王子健程五一

煤矿安全 2019年9期

王子健，程五一

（中国地质大学（北京）工程技术学院，北京100083）

煤与瓦斯突出防治工作是我国煤矿安全技术研究的重要课题，煤与瓦斯突出预测是煤与瓦斯突出防治工作的首要环节[1-2]。我国将突出预测划分为区域性突出预测和工作面预测，区域预测的任务是将突出危险区域划分出来，为后续工作面的防突设计以及防控措施的选择提供依据，煤与瓦斯突出区域预测瓦斯地质方法为常用的区域预测方法[3-8]。如区域预测结果可靠性过低，会造成防突措施选择错误，相应地增加防止突出工程量。因此煤与瓦斯突出区域预测瓦斯地质方法的预测结果可靠性的研究对正确评估防突措施的选择具有重要作用。

1 基于瓦斯地质分析的煤与瓦斯突出区域预测

基于瓦斯地质分析的区域预测方法认为煤与瓦斯是地质历史的产物，是地质体的一部分，瓦斯的形成与赋存受地质条件控制，煤与瓦斯突出受煤的赋存特征、地质构造条件、围岩透气性等参数控制。结合突出分布规律与地质构造情况在已开采区域建立能够反映预测综合指标与地质因素之间定量关系的模型。并利用模型在具有相似地质条件的未开采区域进行外推，从而对未开采区域进行预测[9-10]。

1.1 瓦斯地质分析选取的区域预测指标

瓦斯地质分析煤与瓦斯突出的区域预测，需结合当地煤的特性，选取与煤与瓦斯突出相关性大的指标。结合红菱煤矿实际，采用基岩厚度、煤层厚度、夹石厚度、煤层变异系数及含砂率作为预测指标。

为保证建立的预测模型的准确性，以文献[9，11]中的红菱煤矿12 煤层老区数据为基础，结合红菱煤矿老区12 煤层历年突出表，根据每次突出事故中涌出的煤量或瓦斯量，采用文献[12]中的式（1）计算突出扩散影响范围，补充突出点[9，11-12]。经过补充和筛选，最终选取56 个钻孔数据，突出点32 个，不突出点24 个。

式中：r 为突出影响半径，m；Q 为瓦斯涌出量，m3；W0为煤层瓦斯含量，m3/t；为煤层厚度，m；ρ为煤的密度，t/m3。

1.2 预测模型建立及其区划结果

结合沈阳红菱煤矿开采以及以往资料，选用fisher 判别方法构建煤与瓦斯突出区域预测模型，得到的最终模型如式（2），得到的临界值为0.310 5，大于临界值判定为突出状态，小于临界值判定为安全状态。

式中：Y 为预测综合指标；x1为基岩厚度，m；x2为煤层厚度，m；x3为夹石厚度，m；x4为煤层变异系数；x5为含砂率。

根据式（2）所得到的预测结果利用surfer 软件绘制等值线图，并将发生突出及突出预兆的点标记出来，红菱煤矿突出预测综合指标Y 区划图如图1。

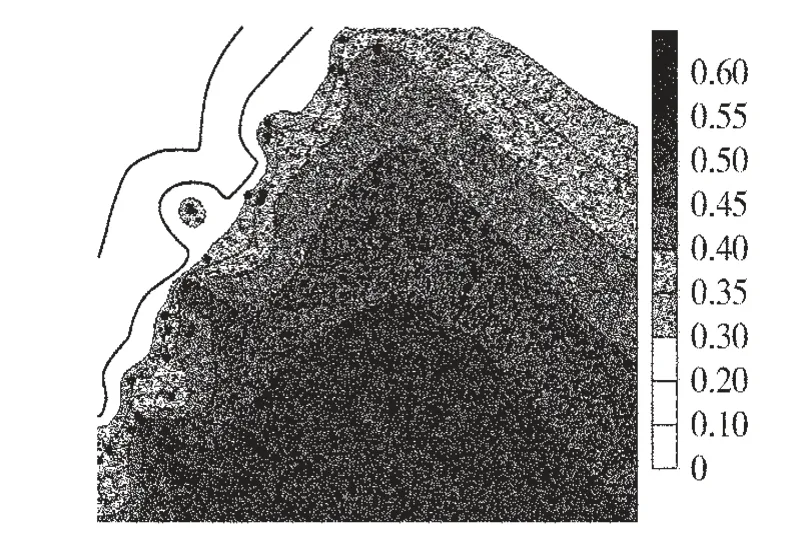
图1 红菱煤矿突出预测综合指标Y 区划图

2 煤与瓦斯区域预测的可靠性分析

煤与瓦斯区域预测的可靠性是指根据区域预测所区划的区域在矿山开采过程中，能够保障不受突出煤层威胁的能力。这种能力可以利用概率表示，即预测的可靠度[13]。煤与瓦斯区域预测可靠性预计是指在以往得到的突出数据和相关资料基础上，评估煤与瓦斯区域预测在煤矿开采过程中所能达到的可靠性水平。因此要想进行区域预测结果的可靠度预计，首要任务是进行煤与瓦斯区域预测的可靠性分析。

对预测进行可靠性分析，煤岩材料受应力（包括地应力、瓦斯压力、构造应力等各种外界力）与煤岩强度存在小概率干涉区域造成的结果，而这小概率事件决定了煤与瓦斯突出过程预测结果的不可靠[13]。预测结果出现不可靠的原因，一方面由于预测指标获得时的随机性和离散性，另一方面由于预测模型运算导致偏差积累。而从采样到运算得到预测结果的过程中都有可能存在不确定性。即包括采样过程中产生的不确定性，由于仪器和环境造成的不确定性，测量人员的不确定性，区域预测过程中产生的不确定性图如图2。在假定预测模型正确的条件下，预测结果的不确定性主要是由数据的不确定性决定。要想进行煤与瓦斯突出区域预测结果的可靠性预计，首先要对预测指标数据的不确定性进行描述，根据国家标准，采用不确定度来表示[14]。

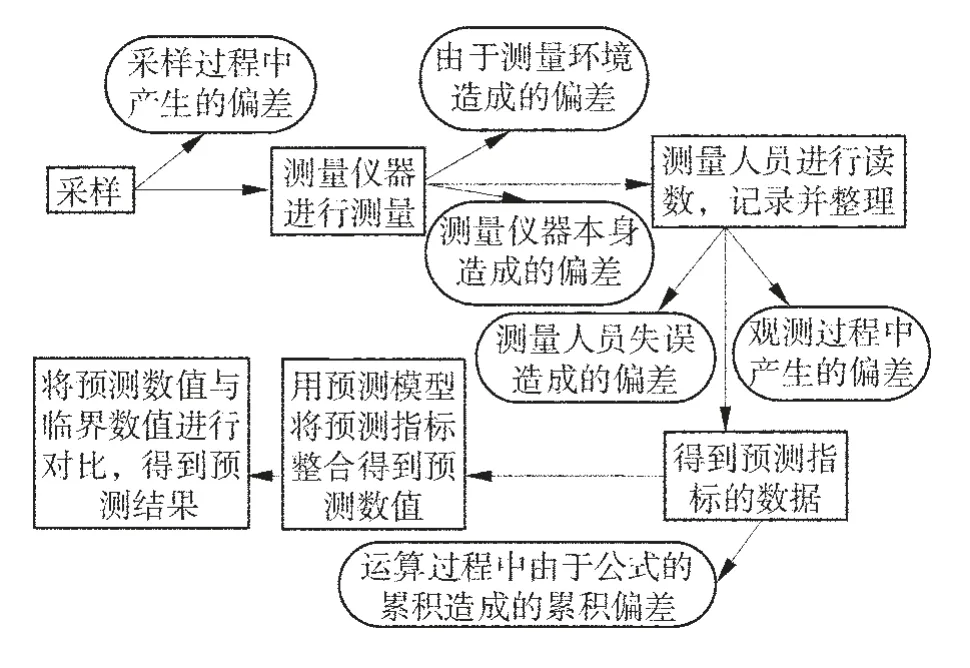
图2 区域预测过程中产生的不确定性图

3 区域预测指标的不确定性分析

3.1 测量不确定度的类型

测量不确定度用以表征合理赋予被测量值的分散性[14-15]。测量不确定度通常用标准差，标准差的给定倍数，置信区间的宽度来表示。对于不确定度的评定通常分为A 类评定和B 类评定。

用统计的方法计算得出不确定度的方法称为不确定度的A 类评定，所得到的不确定度称为A 类标准不确定度。通常要求对于待测参数取几组重复测量，对得到的数值进行计算得到A 类标准不确定度。

通过统计方法以外的任何方法所求得的不确定度的方法称为不确定度的B 类评定，所求的不确定度称为B 类标准不确定度。如观测不确定度，测量仪器不确定度等等。B 类评定往往依据计量工具的检定证书、标准、技术规范、手册上所提供的技术数据，国际上公布的常数与常量等[16]。

式中：uB为B 类标准不确定度；a 为随机变量变化极限范围的1/2，称为半宽；k 为包含因子。

当相关信息给出相应包含因子时，可直接使用；未给出包含因子时，应通过随机变量的分布情况选取相应包含因子，常用分布的包含因子k 值选取见表1。当无法确定分布类型时，可按均匀分布进行估计。在选取煤与瓦斯突出指标时，由于指标通常由于勘探过程得到，很难进行多次重复测量，因此通常采用B 类不确定度的评定方法。

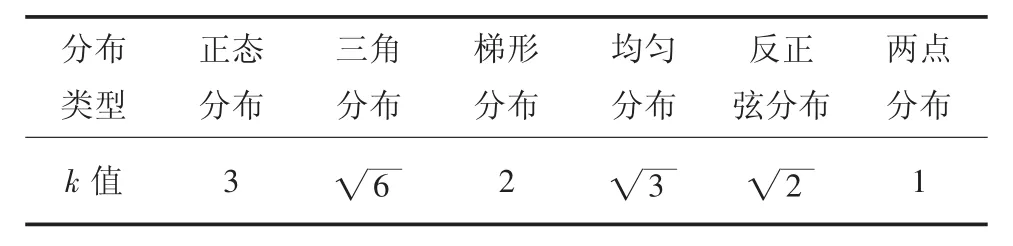
表1 常用分布的包含因子k 值选取

3.2 测量不确定度的合成与传播

1 个指标可能同时存在不同的不确定度分量，在分别依据A 类评定或B 类评定求出相应的不确定度分量后，通常采用平方和法进行不确定度的分量合成：

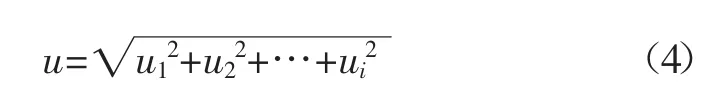
式中：u 为合成的不确定度；i 为不确定度分量的个数。

在进行指标的测量与搜集过程中，有些指标可以直接测量；有些指标由于测量条件等原因不能直接测量，需通过其他能够直接测量的量计算而成。在这个过程中，间接量的测量不确定度可由直接量的测量不确定度求出，称为测量不确定度的传播。

若间接量y 可由n 个变量通过式（5）组成：

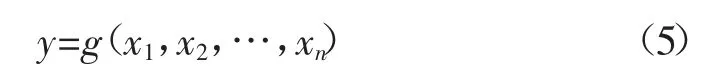
则间接量y 的标准不确定度u（y）得：

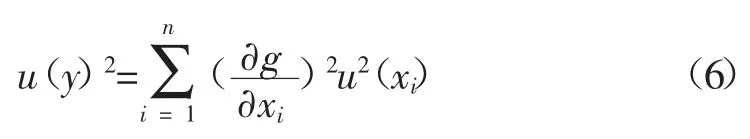
式中：u（xi）表示各输入量的标准不确定度。

3.3 红菱煤矿区域预测不确定度的计算

红菱煤矿的基岩厚度、煤层厚度、泥砂岩厚度通常在钻井勘探的时候进行测量，由于技术条件有限，很难进行多次独立测量，因此这3 个指标的不确定度产生多为仪器产生的偏差以及测量人员的观测不确定度，可以利用上述B 类不确定度的方法进行计算。要进行B 类不确定度的方法，首先应知道指标的最大允许不确定度。

红菱煤矿的煤层厚度通过钻探确定，根据现行的《煤田勘探钻孔工程质量标准》中规定[17]，钻探所确定的煤层厚度及最大允许不确定度，可以与可靠的测井资料验证比较所得，具体关于煤层厚度的规定见表2。红菱煤矿煤层均为优质煤，因此按照表2可以取得各个钻孔煤层厚度的最大允许不确定度，煤层厚度为长度测量，根据中心极限定理，煤层厚度的分布可看作正态分布，根据表1 取包含因子k=3，根据式（3）可以计算各钻孔煤层厚度的不确定度。

夹石是影响煤层瓦斯含量的重要因素，又称为煤矸石。根据《煤田勘探钻孔工程质量标准》[17]，夹石厚度的规定见表3。夹石厚度同样为长度测量，因此夹石厚度的分布可看作正态分布，取包含因子k=3，根据式（3）可计算各钻孔夹石厚度的不确定度。

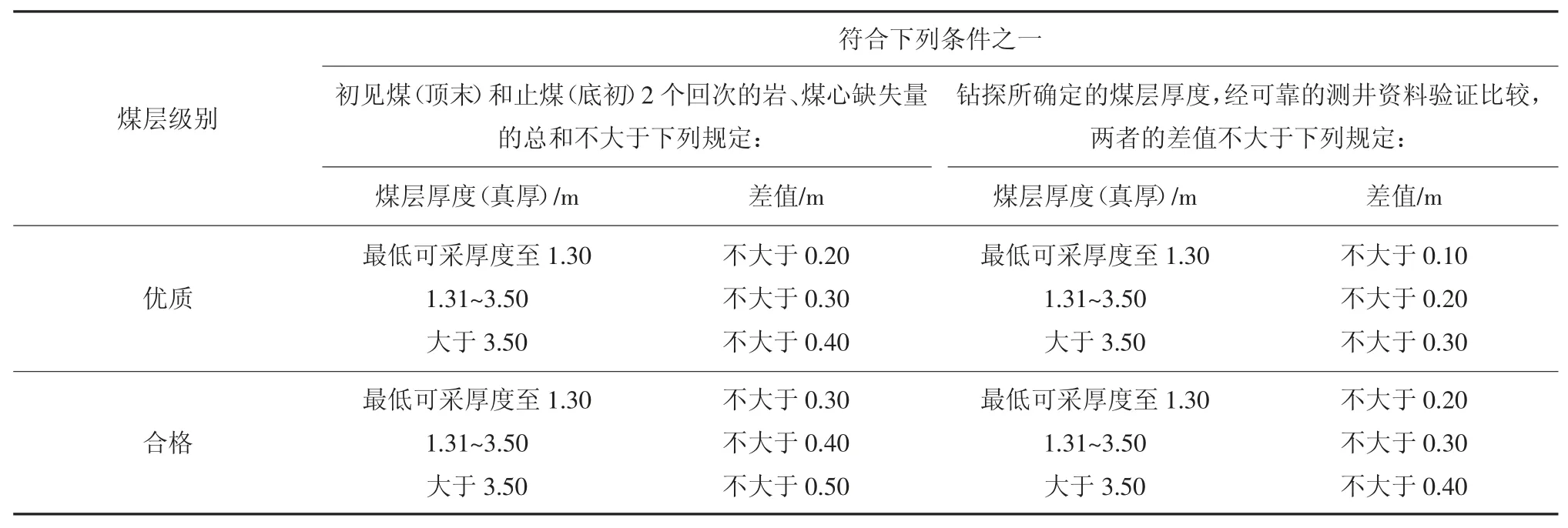
表2 《煤田勘探钻孔工程质量标准》关于煤层厚度的规定

基岩厚度反映了漫长地质历史期间内煤层的埋藏条件和构造形态，能够较好的表征瓦斯的赋存条件，通常用煤层的深度减去第三第四纪的沉积物的厚度求得基岩厚度，第三第四纪沉积物的厚度可近似于常量，因此基岩厚度的不确定度与煤层深度的不确定度相同。现行的《煤田勘探钻孔工程质量标准》中规定[17]，钻探和测井分别确定的煤层深度差，在500 m 内（包括500 m）时，不大于1 m；大于500 m 时，不大于2 ‰。按照上述方法可知煤层深度的最大允许不确定度，也可求出基岩厚度的最大允许不确定度，根据中心极限定理，基岩厚度近似于正态分布，取包含因子k=3，根据式（3）求得基岩厚度的不确定度。

含砂率是反映煤层围岩透气性的一项指标。顶板含沙率是指煤层顶板范围一定厚度层段内砂岩厚度与统计厚度的比值[9]。由于当地情况，含砂率按照30 m 内的泥砂岩厚度计算，含砂率的不确定度可以用泥砂岩厚度的不确定度除30 得到；按照《煤田勘探钻孔工程质量标准》[17]，砂岩厚度在煤层顶板范围内准确丈量钻具，且进行合理平差，通常不确定度最大不超过1.5‰。同煤层厚度一样，砂岩厚度也近似看作正态分布，取k=3 进行计算，可得到砂岩厚度的不确定度，进而求出含砂率的不确定度。

煤层变异系数是定量描述煤厚在一定范围内的变化趋势的指标，为了能够将整个矿区覆盖起来，选取了1 个钻孔，以250 m 为计算范围半径，在这个钻孔内选取煤厚点，计算出钻孔的煤厚变异系数。煤层变异系数1 个无量纲的量，通常将其不确定度近似看作0。

经上述分析，求得的红菱煤矿区域预测的各个预测指标的不确定度见表4。

表3 《煤田勘探钻孔工程质量标准》关于夹石厚度的规定

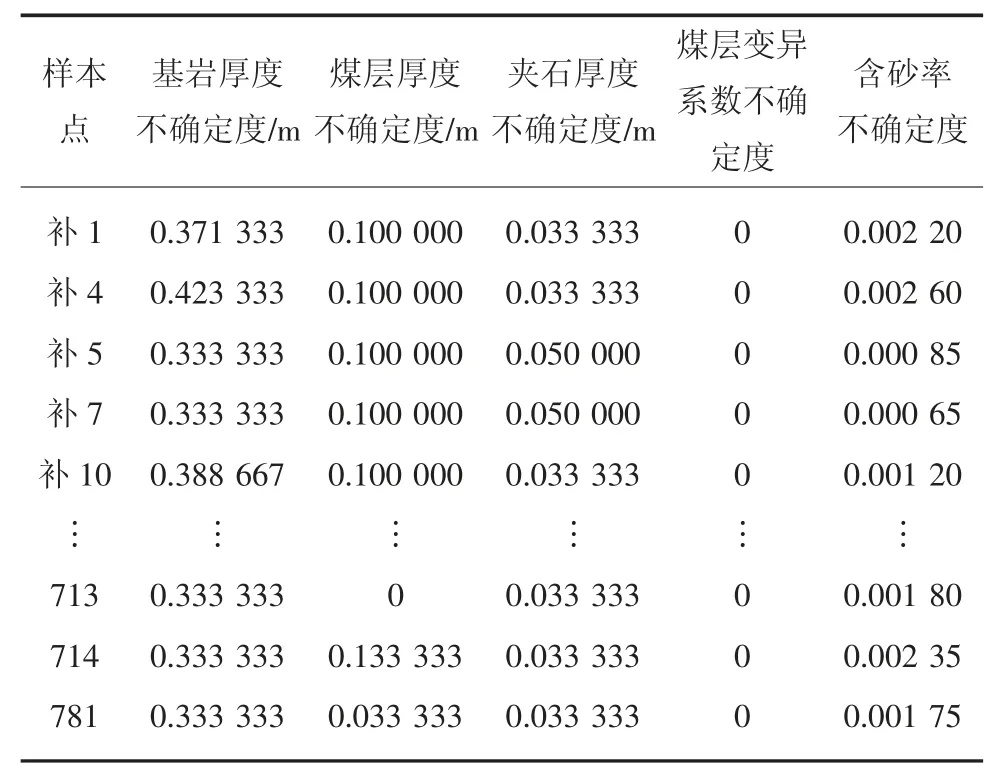
表4 红菱煤矿区域预测各指标的不确定度

4 煤与瓦斯区域预测可靠度预计原理

进行可靠度的预计，需构建功能函数来判断煤层的突出状态，由前文可知，根据预测模型可以构建如下功能函数Z：

式中：Y'=f（X）为煤与瓦斯突出区域预测建立的预测模型；y0为预测模型的临界值。

功能函数Z 将系统分为3 个状态，Z＞0 时为突出状态，Z＜0 时为安全状态，Z=0 时为极限状态。假设功能函数Z 的预测值分布函数为h（z），进行定值计算时得到的值为，预测时采用的往往是判断煤层的突出状态，而忽略了数据的不确定性。因此区域预测的可靠可以理解为，用h（z）判断的煤层突出状态与判断的煤层突出状态一致，即h（z）＞0，区域预测的可靠性状态如图3。

设实际如果知道z 的概率分布即可求得区域预测的可靠度，根据前文不确定度的计算，可求得z 的不确定度uz，根据大数定理与中心极限定理，可知不确定度通常服从正态分布，因此h（z）服从（，uz）的正态分布，令，则T 服从（0，1）的标准正态分布，且式（8）可以进行下列转化：

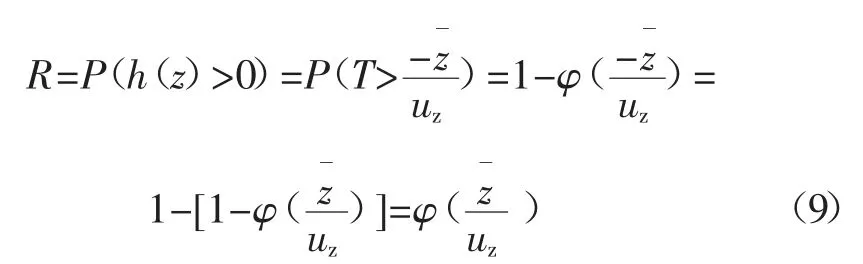
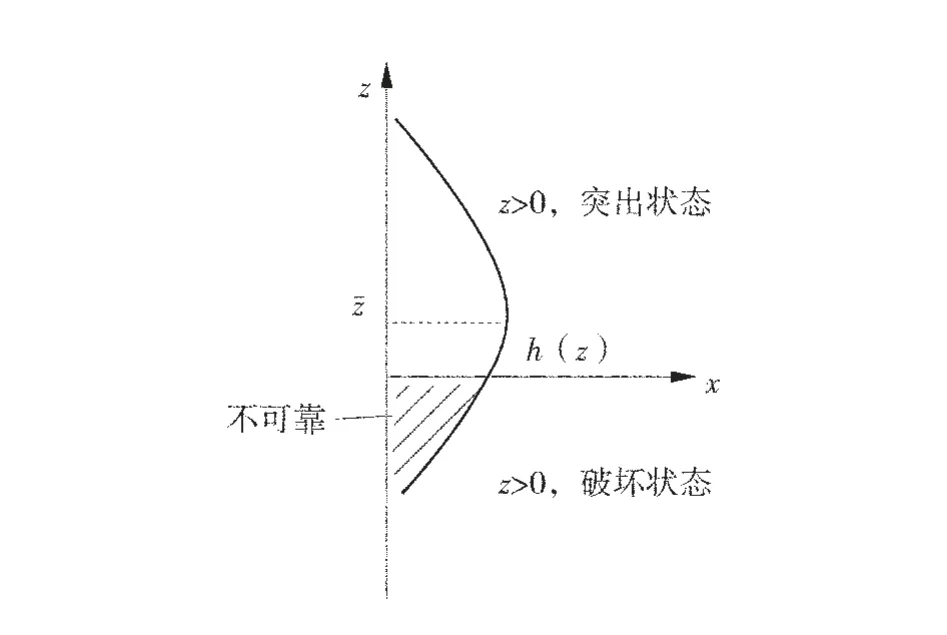
图3 区域预测的可靠性状态图

区域预测可靠度值通过查标准正态分布表即可求得。

将上述结果进行整理可得区域预测可靠度为：

因此区域预测的可靠度可以按照式（11）求得，并查标准正态分布表可得。

5 红菱煤矿煤与瓦斯区域预测可靠度预测

按照上述步骤对红菱煤矿瓦斯地质分析的区域预测结果进行可靠度计算，预测结果可靠度见表5，并用surfer 方法将各钻孔的可靠度绘制成平面图，瓦斯地质分析区域预测可靠度图如图4。

表5 预测结果可靠度表

图4 瓦斯地质分析区域预测可靠度图

根据图4 和表5 可以看出，56 个钻孔中51 个钻孔的预测结果的可靠度为在0.99 以上，表明这51个钻孔预测结果具有很高的可靠性。另外补5、补20、679 以及补14 4 个钻孔预测结果的可靠度在0.90 以上，而A4 钻孔预测结果的可靠度为0.833，预测结果可靠度最低。在预测的56 个钻孔中，预测为突出的钻孔为32 个，不突出的钻孔为24 个。而在实际开采过程中，判定为突出的32 个钻孔中A4 钻孔并没有发生突出，其余31 个钻孔发生了突出；判定为不突出的24 个钻孔在实际开采中均没有发生突出。这表明实际开采结果与区域预测可靠度预计结果一致，证明区域预测可靠度预计方法的准确性。分析可靠度较高的原因，计算采用的数据是国家标准中的数据，而国家标准是经过无数次实践和理论推倒的结果，制订的标准本身具有高度可靠性。

在生产过程中经常会出现不确定度不稳定的情况，为探究数据的不确定度对于预测结果可靠度是否有影响，将每个指标的最大允许不确定度分别扩大为原来最大允许不确定度的2 倍，3 倍以及4 倍，并将最大允许不确定度扩大后各钻孔预测结果的可靠度进行整理，最大不确定度增幅区间的预测结果可靠度见表6。

由表6 可知，当最大允许不确定度逐渐变大时，有些钻孔预测结果的可靠度一直保持0.99 以上的水平；有些钻孔的预测结果的可靠度随着最大允许不确定度的增大而降低。当最大允许不确定度变为原来的4 倍时，A10、419 及654 这3 个钻孔的预测结果可靠度在0.85 以上，仍维持可靠度较高的水平；补5、补20 与679 这3 个钻孔预测结果的可靠度在0.7 与0.8 之间，处于较低的水平。而A4 和补14 这2 个钻孔预测结果的可靠度分别为0.59 和0.65，说明此时2 个钻孔的预测结果具有较强的不可靠性。

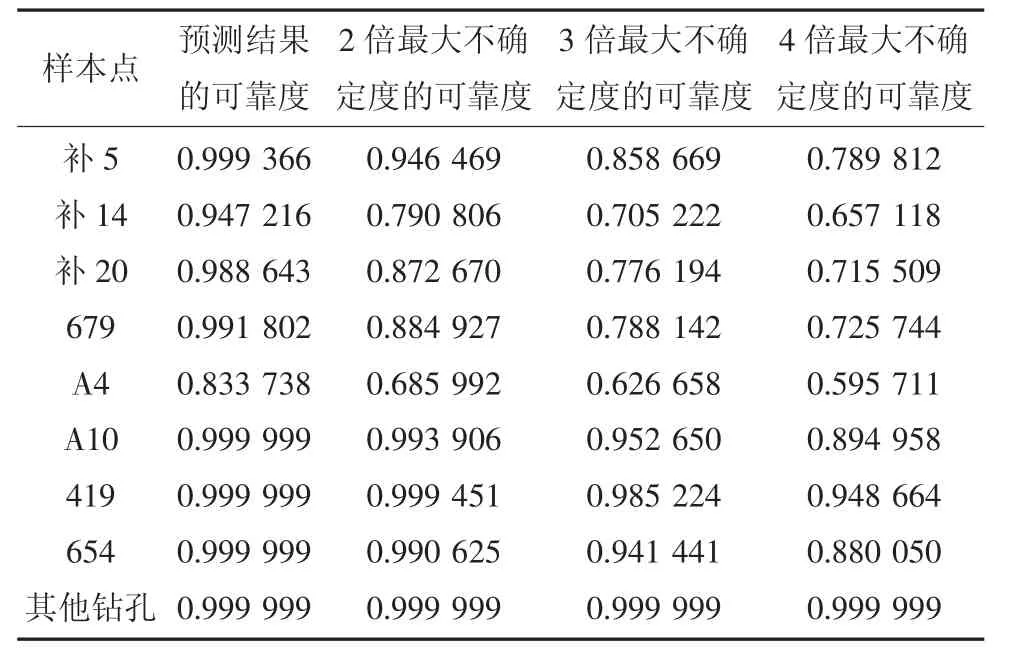
表6 最大不确定度增幅区间的预测结果可靠度表

之所以会出现当数据最大允许不确定度增大有些钻孔预测结果可靠度降低有些钻孔预测结果可靠度不变的情况，原因有2 方面：

1）煤与瓦斯突出区域的预测结果是通过预测模型得到的预测值与临界值比较大小所判定，对于正确的预测模型来说，预测模型会通过运算抵消一部分数据不确定度波动对预测结果的影响。数据不确定度波动时，当预测模型能够抵消数据不确定度波动对预测结果的影响时，无论数据不确定度如何波动，钻孔的预测结果的可靠度依然保持不变。

2）当预测模型不能抵消数据不确定度波动对预测结果的影响时，数据不确定度的增大会导致钻孔预测结果的可靠度逐渐降低。

因此在测量过程中，一定保证数据的稳定性，确保不会出现大的波动，这样才能保证由数据的不确定性求得的区域预测结果的可靠度稳定。