基于支路势能脊方法的风电电力系统暂态稳定评估与控制

王 曼

（南京工程学院，江苏 南京 211167）

0 引言

由于采用了不同于传统同步发电技术的风电机组，大规模风电并网给电力系统稳定运行带来了新的挑战。风电电力系统的暂态稳定评估更是当前风电并网研究中的重点。

目前，电力系统暂态稳定评估方法主要有时域仿真法、能量函数法和人工智能方法[1]。时域仿真法通过求解全系统的微分代数方程组，利用扰动后状态变量的变化规律对系统运行的稳定状态进行评估。此方法能够计及元件详细模型，计算结果精确可靠；但耗费机时、计算量大始终是限制该方法广泛应用的瓶颈；另外也很难给出系统稳定裕度的定量指标[2]，一般用作离线分析和其他分析方法的校验手段。人工智能方法基于经验信息，通过建立输入和输出间的非线性映射关系，为系统运行状态的判别和控制做出决策[3]。自动学习的高效算法和大量精确反映系统特征的学习样本的获取[4]是目前关于人工智能方法研究的关键。能量函数方法基于Lyapunov稳定定律，通过构造包含系统运行和干扰等大量信息的能量函数，直接判断系统暂态稳定性。Padiyar[5]建立了结构保持模型下包含阻尼、自动励磁调节系统的详细发电机能量函数，研究了这种详细模型能量函数在判别多机系统暂态稳定的有效性。蔡国伟[6]提出了支路势能函数的概念，认为系统势能由分布在系统中所有支路势能之和构成。Ando[7]提出了势能脊的概念，认为系统故障后越过势能脊说明系统失去稳定性；但目前尚未有将势能脊方法应用于风电电力系统的研究，能量函数方法在风电电力系统暂态稳定中的研究也不够丰富。

本文将支路势能概念与势能脊方法相结合，提出了支路势能脊研究方法和基于支路势能脊的支路暂态稳定指标。利用支路势能脊仅仅通过支路势能及其导数进行计算，无须计及复杂发电机机组模型的特点，将其应用于风电电力系统，使用支路暂态稳定指标判断系统受干扰后的稳定薄弱环节，并通过在薄弱支路投切晶闸管控制串联补偿装置TCSC（thyristor controlled series compensator）提高系统的暂态稳定性。

1 支路势能脊法理论

1.1 支路势能函数

依据支路势能理论[8-9]，对于一个有n个节点、m台同步发电机、l条支路的多机系统，系统的暂态势能VPE可以描述为

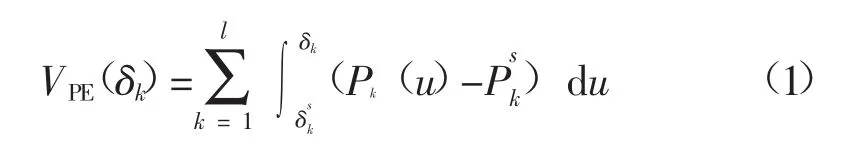
式中：δk和表示故障后某时刻和故障后系统稳定平衡点处第k条支路两端相角差；Pk和为该时刻和故障后稳定平衡点第k条支路的有功潮流。

第k条支路沿故障后轨迹的势能VPE,k（δk）可表示为

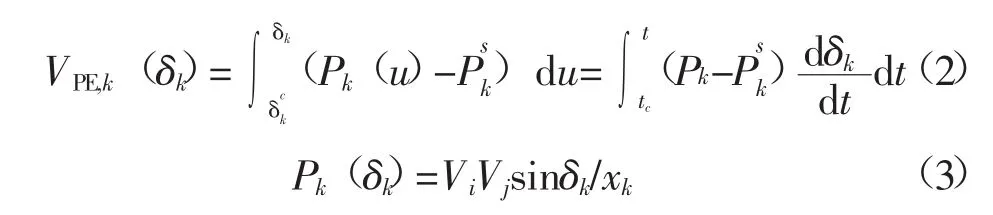
式中：tc为故障切除时刻；Vi、Vj为支路k两端i、j点的电压幅值；xk为支路k的电抗。

由于同调区内节点相角具有相同的变化规律，可认为同调区内势能为0，系统势能可以简化为系统中所有临界割集支路势能之和。

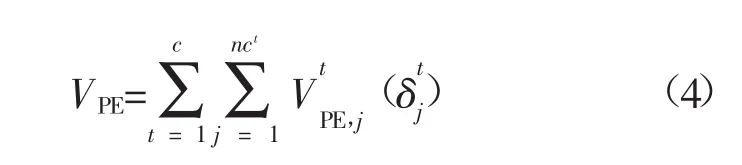
式中：c为系统临界割集数量；nct为第t个割集中的支路数；VPE，j为表示属于割集t的第j条支路势能。

又因同一割集内所有支路两端电压Vi、Vj和相角差σk分别具有相同变化规律，所以某割集支路势能可以表示为割集中任意支路势能的倍数，故系统简化势能式（4）还可写为

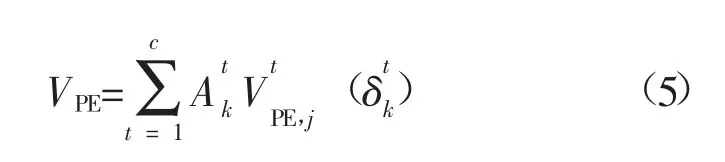
1.2 支路势能脊法

势能脊方法继承发展了暂态稳定势能边界曲面 PEBS（potential energy boundary surface） 方法,该方法假设系统持续故障轨迹穿越势能边界曲面，势能在此刻取得最大值；但Ando通过分析仿真发现，实际系统在很多情况下持续故障的势能轨迹并不一定穿越势能边界曲面，导致PEBS方法有较大的分析误差。“势能脊”（potential energy ridge）方法的提出，提高了算法的可靠性。所谓“脊”可以理解为势能在支路相角差空间的所有最大值点所构成的集合。体现了在δ空间中等势能面作用在δk方向上的作用力。势能VPE,k在到达脊时在δk方向最大，表明在系统轨迹越过势能脊后，被拉向背离稳定平衡点的方向，故系统失去同步。

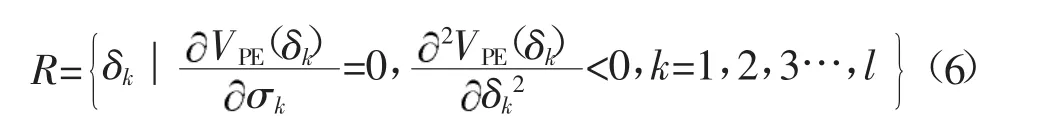
由支路势能表达式（2）和系统简化势能的表示式（5），系统的支路势能脊即为

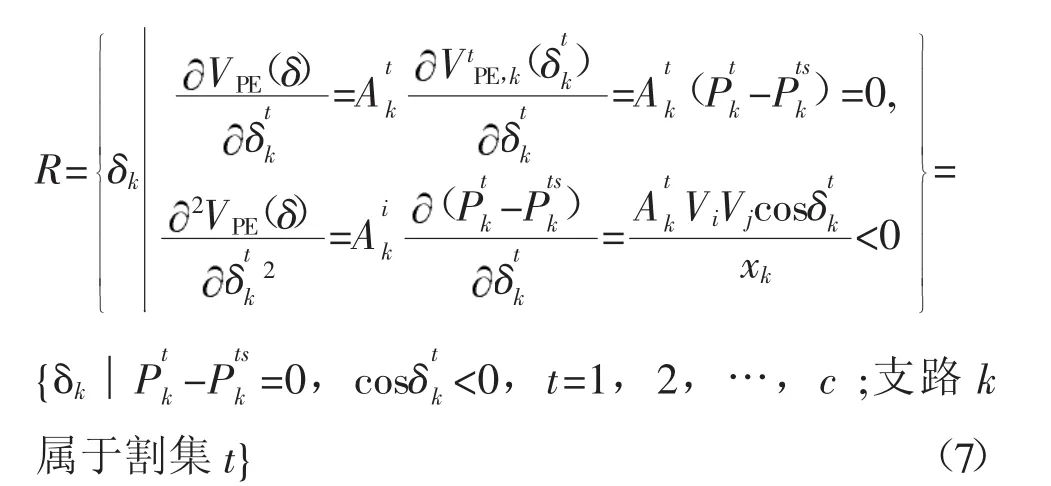
1.3 基于支路势能脊的支路暂态稳定指标和系统

薄弱环节的判别

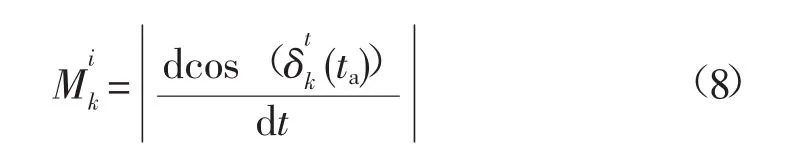
式中：ta为首次取得极小值的时刻，指标越大，说明该条支路越不稳定。

由此，可依据各支路稳定指标判断系统薄弱环节：故障后计算各支路暂态稳定指标，Mik最大的支路即为系统薄弱环节，由其构成的割集即为系统暂态失稳的临界割集。在系统薄弱环节安装合适的补偿装置就有可能提高系统的暂态稳定性。

2 采用支路势能脊法的风电系统暂态稳定判别与控制

支路势能脊方法以系统割集支路势能及其导数的变化率作为系统暂态稳定和支路稳定程度的判别依据，不涉及发电机组具体数学模型，具有普遍的适应性，同样适用于包含风电场的电力系统。

作为目前风电市场上的主流机型，异步运行的双馈异步风电机组不存在功角失步问题；但高渗透率的风电功率的接入，对系统中同步机组的功角稳定带来深刻影响。

本文以支路势能法研究风电电力系统暂态稳定性，通过计算系统受扰后各支路势能及其一阶、二阶导数，判断系统是否越过势能脊，对系统是否保持暂态稳定做出评估，并依据各支路的暂态稳定指标，在失稳前识别系统稳定的薄弱环节，通过在稳定薄弱支路投切TCSC，以提高系统暂态稳定性。

可控串补TCSC通过快速、连续调节串入电网的电抗，可以减小机组间的电气距离，提高电网的输送能力，增加机组的同步力矩，从而提高系统的暂态稳定性。

以单机无穷大系统（如图1所示）为例，由于装设TCSC后发电机和大系统之间的等值电抗有所减小，若发电机空载电动势Eq和无穷大母线电压U保持恒定，补偿前后的功角特性曲线分别如图2中实线和虚线所示。可见，同样原动机输入机械功率P0情况下，装设了TCSC的系统大大提高了系统的能量极限，能够增加系统故障后的减速面积，提高系统的暂态稳定性。

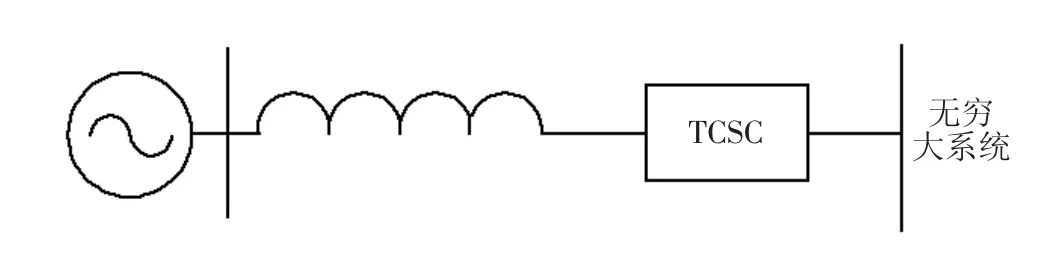
图1 单机无穷大系统装设TCSC

图2 单机无穷大系统装设TCSC的功角特性

多机系统中，大干扰后系统稳定薄弱环节支路承担的暂态势能出现了急剧变化，抑制薄弱环节支路的暂态势能变化能够有效避免暂态失稳，防止系统的同步在此处被“撕裂”。本文正是依据风电系统中各支路暂态稳定指标大小识别系统稳定的最薄弱支路并作为TCSC的安装点，投切补偿装置，以达到提高系统稳定性的目的。

3 含风电WSCC9节点系统暂态稳定分析

为了验证支路稳定指标判别系统稳定薄弱支路的有效性和TCSC对提高多机系统暂态稳定的效用，本文以修改的WSCC 3机9节点系统进行仿真分析。系统如图3所示，同步发电机采用经典二阶模型；负荷为恒功率模型；使用额定装机容量为100 MVA的双馈异步风电机组替换原系统中母线3处的同步发电机组，双馈风电机组采用四阶模型，模型和参数参见文献 [11]。风速为双参weilbull模型，参数：K=2，C=20。系统仿真步长为0.05 s。假设母线7处在t=1 s时发生三相短路故障，t=1.25 s时清除故障，故障清除后系统结构与原系统相同，则式（7）中即为系统故障前稳定状态时支路k流经的功率。由支路势能脊方法，连接母线7、8的支路2在t=1.35 s时刻越过势能脊，系统失去暂态稳定。同步发电机1、2功角时域仿真曲线如图4所示，支路稳定指标如表1所示。

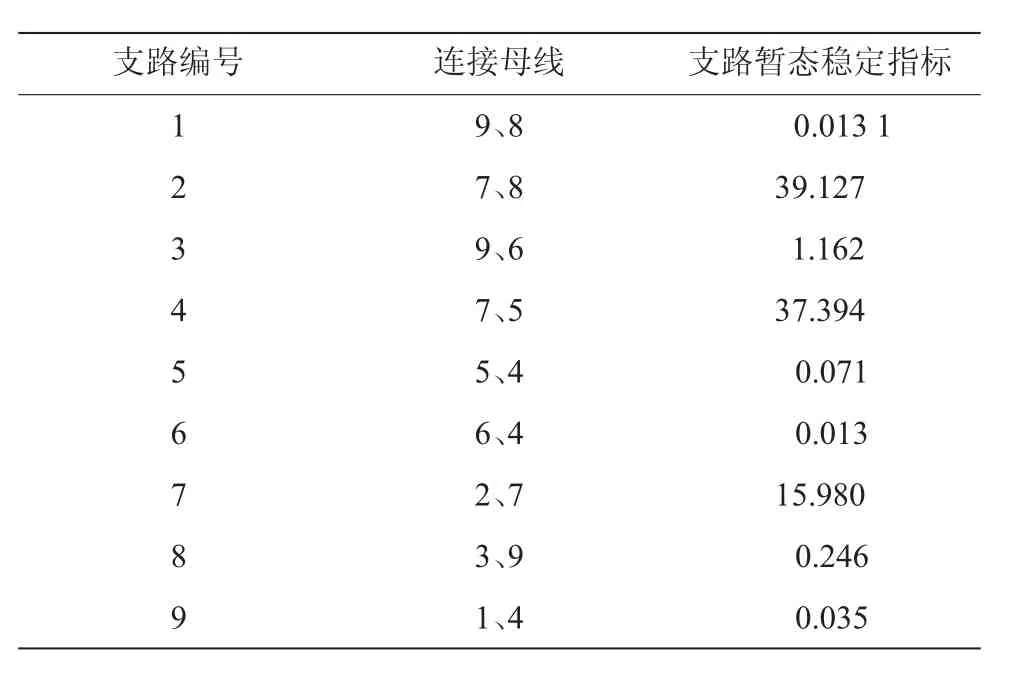
表1 含风电WSCC9系统三相短路故障时的系统支路暂态稳定指标

根据支路稳定指标，连接母线7、8的支路2和连接母线7、5的支路4为系统稳定的薄弱支路。在系统的这两条支路上装设TCSC，如图2中所示，可控串补的最大补偿度分别为50%和60%。安装TCSC之后，同样在母线7处三相短路，故障持续0.25 s后清除故障，系统不再越过势能脊，系统恢复为稳定状态。此时系统中另外2台同步发电机转子角速度之差的变化规律如图5所示。投切了可控串补之后，同样故障下，风电系统由暂态不稳定恢复到了暂态稳定，证明了支路暂态势能指标在判别系统薄弱支路的有效性以及TCSC对提高风电系统暂态稳定性的作用。

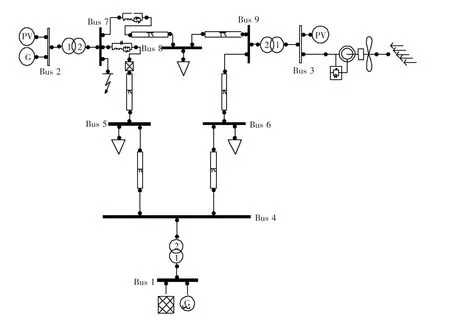
图3 WSCC9 BUS系统图

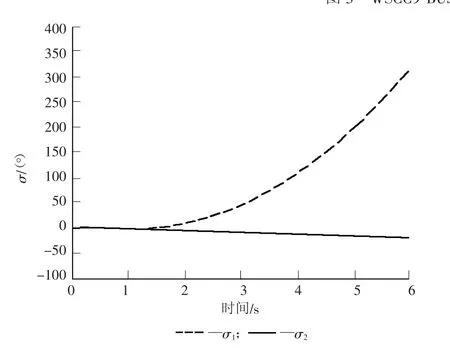
图4 未装设TCSC系统故障时发电机功角摇摆曲线

图5 投切TCSC的发电机1、2功角差值曲线

4 结论

支路势能法与暂态势能脊概念结合，给出了基于支路势能脊的支路暂态稳定指标；将其应用于含风电的多机系统，验证了这种支路暂态稳定指标在风电电力系统识别稳定薄弱支路的适用性。后续工作可以进一步研究故障轨迹预测及支路暂态稳定指标对稳定薄弱支路的超前识别问题。