谐振式陀螺全角模式误差来源与接口技术

李 崇，宋大雷，宫宜辉 ，杨 华，李坤乾

（1.中国海洋大学工程学院，青岛266100；2.中国海洋大学信息科学与工程学院，青岛266100）

0 引言

谐振式陀螺是一种重要的测量旋转的传感器,可为消费电子、航空航天、无人驾驶汽车等领域提供导航、航姿指引等核心功能[1-2]。谐振式陀螺主要分为两类,一类为微机电陀螺（Micro Electro Mechanical Systems Gyroscope,MEMS Gyroscope）[3], 另一类为半球谐振陀螺（Hemispherical Resonator Gyroscope,HRG）[4]。微机电陀螺的优势为带宽大、体积小、功耗和成本低,劣势为测量精度低,半球谐振陀螺则与其特性相反[5]。

全角模式也称为角速率积分模式,是近年来兴起的新型陀螺调制方式。相比于传统的调幅+力平衡的调制方案,全角模式在理论上有无限的带宽,不仅是半球谐振陀螺解决短板的有效方案,也是微机电陀螺迈向超高范围动态测量的途径,被视为颠覆市场的关键技术[6]。全角模式陀螺的最大挑战在于控制其在不影响角度测量的情况下保持振荡。Prikhodko等[7]提出了采用开环的控制方式,允许陀螺自由振荡。采用该控制方式的陀螺可以以很高的速度旋转而不会因延迟引起非线性,但是其漂移仍在 10（°）/h。 Putty 等[8]提出了利用锁相环产生信号维持陀螺振荡,该方式对陀螺误差无补偿且对驱动和读出增益误差特别敏感。Painter等[9]提出了一种基于LabVIEW Simulink的全角模式陀螺可编程控制系统,并给出了一种补偿正交误差的方法。但是,该方式频率是固定的,并且对于快速系统,Simulink控件的实时运行非常困难,限制了系统的稳定性。由于全角模式对机械部分对称性要求极高,且信号调制和控制算法复杂,其误差产生原理和控制系统仍需进一步研究。

本文针对全角模式,首先阐述了其运行原理,然后对机械部分的模态分裂、阻尼不匹配、能量衰减等不理想因素进行了分析讨论,并针对不理想因素提出了相应的器件选型和控制系统方案。

1 全角模式运行原理

对于谐振式陀螺,其理想状态下的动力学方程为[10]

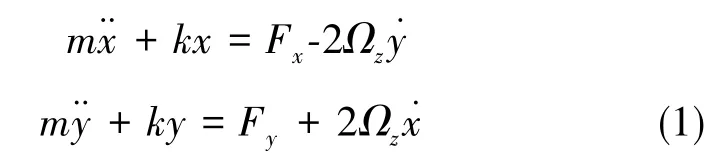
式（1）中,x和y为陀螺的正交谐振子的在x模态和y模态上的位移,m为质量,k为弹簧系数,Fx和Fy为作用在x模态和y模态上的驱动力,Ωz为Z轴上的旋转角速度。

在全角模式运行下,假设系统的初始速度或位移不为0,或使用驱动力Fx或Fy进行初始激励给予一定的初始运动能量。在全角正式运行时,Fx和Fy应等于0。在此前提下,系统对Z轴旋转的响应仅存在自由响应解的形式

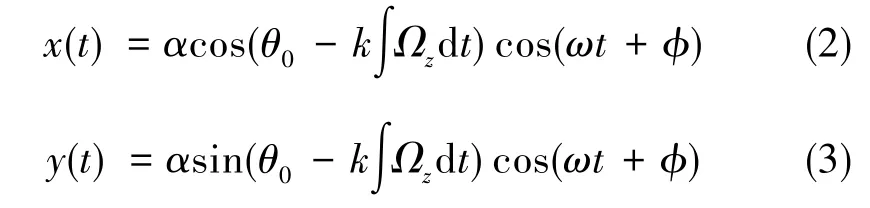
式（2）和式（3）中,α为x模态和y模态初始状态的相关幅值,ω为陀螺的谐振频率,φ为由系统初始状态决定的相位变化。将式（3）和式（2）相除,并求其反正切函数,可得

式（4）中,θ为x模态和y模态运动轨迹的夹角,从而求得Z轴上的转动角度。

相比传统的运行模式,角速率陀螺需要令Fx或Fy将陀螺的一个模态驱动在谐振频率上作为“驱动模态”,另一个模态作为 “响应模态”,其感应模态的时域响应解为[11]

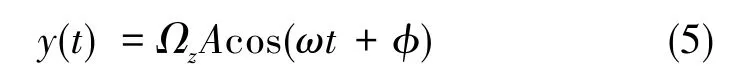
可见,全角模式陀螺和角速率模式的最大的区别在于：角速率模式利用的是陀螺的受迫响应解,而全角模式利用的是在有初始能量下的自由响应解。因此,能否构造出陀螺的自由响应解的工作环境,是全角模式的基础。

2 全角模式误差来源

虽然式（1）～式（4）及其相关讨论指出了理想环境下全角模式的运行原理,但是现实中由于加工误差和客观环境的原因,会给全角模式的实现带来诸多的挑战。其主要误差因素包括存在阻尼系数、模态频率分裂、模态阻尼不匹配等。其动力学模型的表现形式为

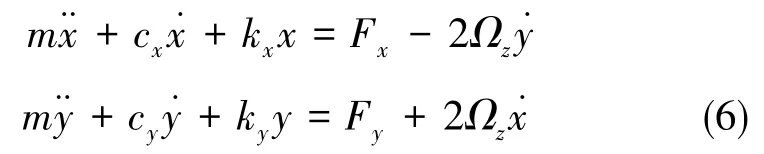
式（6）中,cx和cy为x模态和y模态上的阻尼系数,kx和ky为x模态和y模态上的等效弹簧系数,且两个模态上的阻尼系数和弹簧系数均不相等。

由于（6）式中的不理想因素众多,出于工程的化简及问题的分析考虑,可将各种不理想因素分别添加到理想系统中以考量其影响。

2.1 阻尼与能量衰减

如上文所述,全角模式利用的是振动式陀螺的自由响应解。但由于阻尼的存在,其自由振动会随着时间衰减,从而导致角度检测失效。定义陀螺振动的初始总能量E0为x模态和y模态上驻波的幅值, 结合式（2）、式（3）, 可得

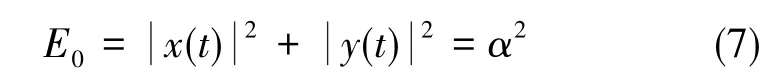
其由于阻尼效应衰减的效应为

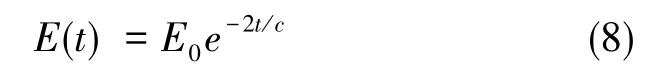
由式（8）可得：当系统阻尼系数小、谐振频率低时,系统的能量衰减速度较慢。

2.2 模态频率分裂

模态频率分裂是另一大阻碍全角模式实现的关键因素。由于加工缺陷和单晶硅晶体分布不均匀等原因,x模态和y模态的谐振频率不可能完全相同,并且频率差会随着时间变化。在此情况下,系统方程为

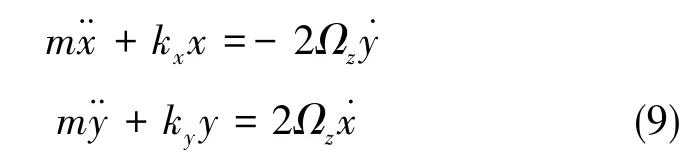
此时,系统的转动惯量H（t）变化可化简为[12]

式（10）中,Hm为系统的最大转动惯量。

分析式（10）可知,在弹簧系数不匹配的情况下,陀螺在全角模式下会进行周期往复运动。但标称的谐振频率越高,其往复运动的周期就越短。

2.3 模态阻尼不匹配

x模态和y模态的阻尼不匹配是一个容易被忽略的因素。同样,由于加工和晶体分布的原因,两者的阻尼是存在差异的。在两模态阻尼不匹配情况下,系统动态方程为

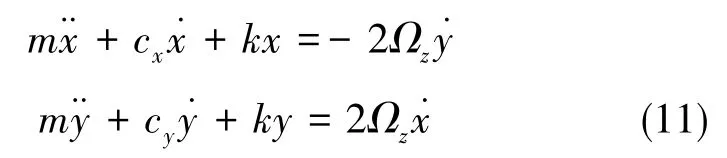
此时,除Z轴的物理旋转外,θ还受到系统本身的干扰[13]

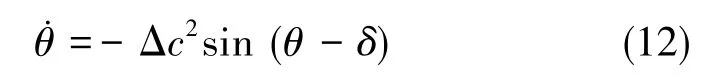
式（12）中,Δc为两个模态的阻尼之差,δ取值与x模态和y阻尼比大小有关。当cx>cy时,δ取值为0°,反之则取值为90°。

由式（12）可知,当Z轴发生旋转时,θ会随着时间的增加最终收敛到阻尼较小的一个轴上。这是因为x模态和y模态上能量耗散的速度不同,从而导致阻尼较大的模态上的能量率先耗散殆尽。

3 器件设计与控制系统

3.1 器件设计

由理论分析可知,模态的频率分裂、阻尼的存在、阻尼的不匹配均为全角模式的不理想因素,但是通过合理的器件设计和选型,可以制造加工出更为适合的全角模式振动式陀螺。

陀螺的阻尼比应尽量设计的小,因为小的阻尼比可使得陀螺的振动能量维持更长的时间,在需要工作时间较短的工况下,甚至可以避免控制系统的介入来降低成本[14]。谐振频率的数值选取是较为矛盾的,较低的谐振频率可以增加陀螺自由震荡的时间,但是也会放大模态分裂的周期振动作用。在保证较大阻尼比的情况下,应尽量保证两个模态阻尼比的一致性来获得更好的稳态性能。如阻尼比不能保证较好的一致性,应尽量减小其谐振频率从而降低影响。

3.2 控制系统

尽管通过加工工艺的改善和关键参数的优化,可以提升振动式陀螺全角模式的性能,但是控制系统的介入仍是实现全角模式不可或缺的途径。全角模式的控制系统如图1所示,陀螺的主要电极有x输入、x输出、y输入、y输出4个。x和y的输出信号由跨阻放大器转换为电压信号,经过模数转换器（ADC）进入数字控制系统,然后再由混频器和低通滤波器分解为基带内的相内、干扰信号（IQ信号）。通过两路（x和y）IQ信号,系统可以通过反正切函数来得到θ。

通过计算IQ信号的幅值,控制系统可得到陀螺的能量,并将此能量维持在一个常数量,从而抵消系统的阻尼效应。陀螺的激励信号由数控振荡器产生,数控振荡器的频率由锁相环回路（Phase Lock Loop,PLL）锁定在陀螺的谐振频率上。激励陀螺的能量总幅度由能量控制回路决定,在x模态和y模态上的能量分解由解算出的θ来决定。当x模态和y模态的信号能量被确定以后,由两路模数转换器（DAC）产生模拟信号,作用在陀螺上。陀螺的频率分裂可由谐振频率调谐电机VT来进行一次性调整[11],阻尼的不匹配可由调节两路DAC的增益来实现。

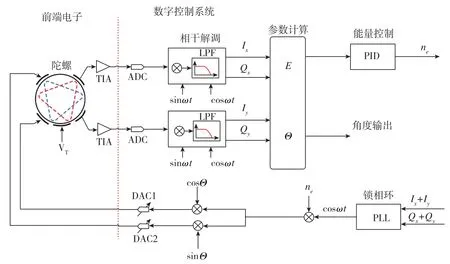
图1 全角模式及其控制系统原理框图Fig.1 Principle block diagram of whole angle mode and its control system

4 原理验证

为了验证陀螺不理想因素和控制系统方案的正确性,利用Matlab Simulink进行仿真实验,其系统框图如图2所示。振动模态1、振动模态2表示陀螺的2个振动模态,4个反馈回路为其弹簧力和阻尼力,两模态之间的连接回路为Coriolis力,最左侧为45°的角度输入,陀螺的标称谐振频率为100Hz。在随后的每个验证过程中,在0.3s时,系统会给予陀螺一个45°的阶跃输入,仿真总时间为5s。x模态和y模态的总行程归一化为[-1,1]范围内。

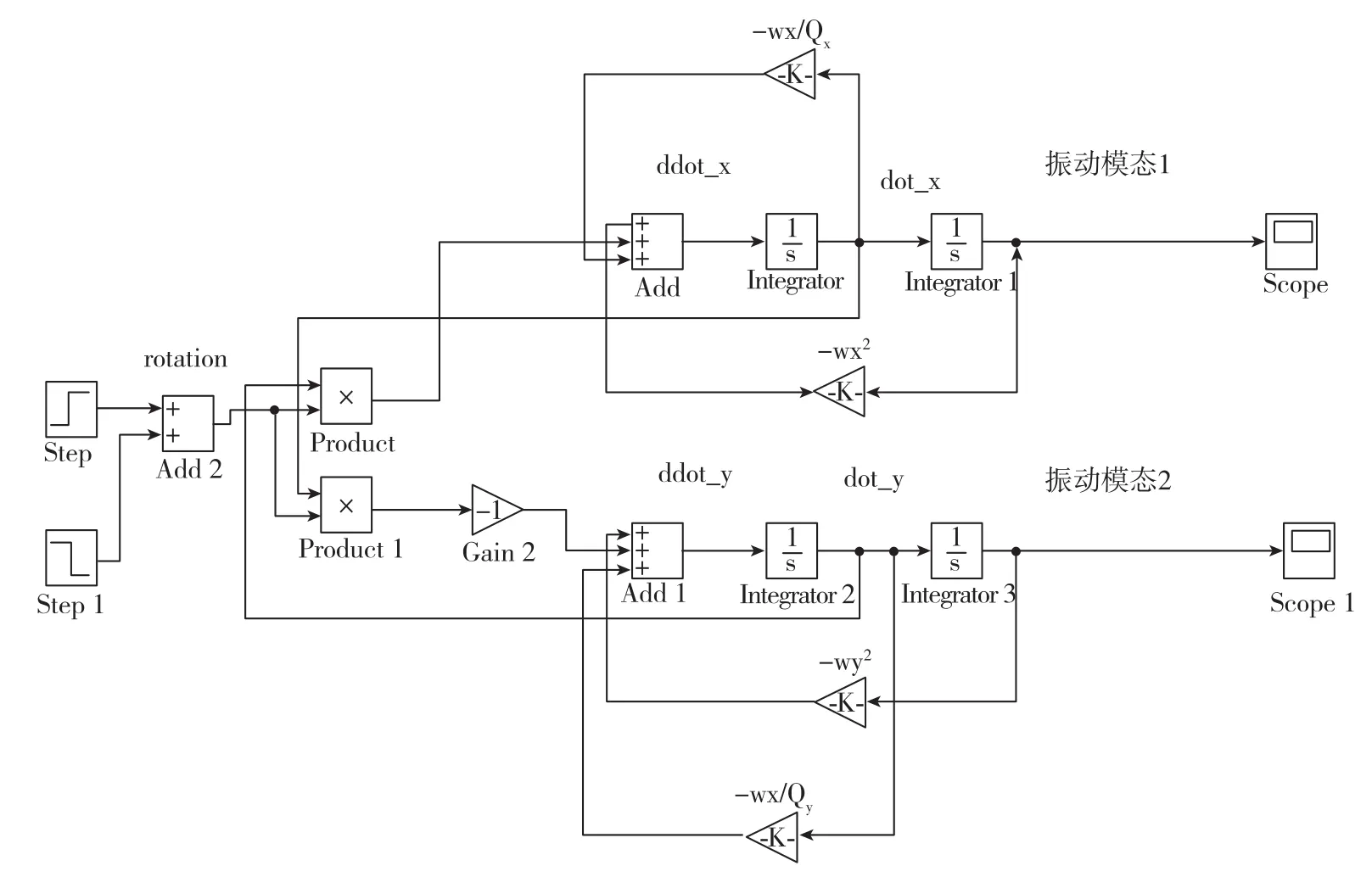
图2 全角模式误差机理仿真框图Fig.2 Simulation block diagram of whole angle mode error mechanism

首先被验证的是陀螺的阻尼效应,如图3所示。在有阻尼存在的情况下,x模态和y模态的运动轨迹虽然随着角度输入而改变,但是由于阻尼的作用,其幅值逐渐衰减直至θ无法被检测。

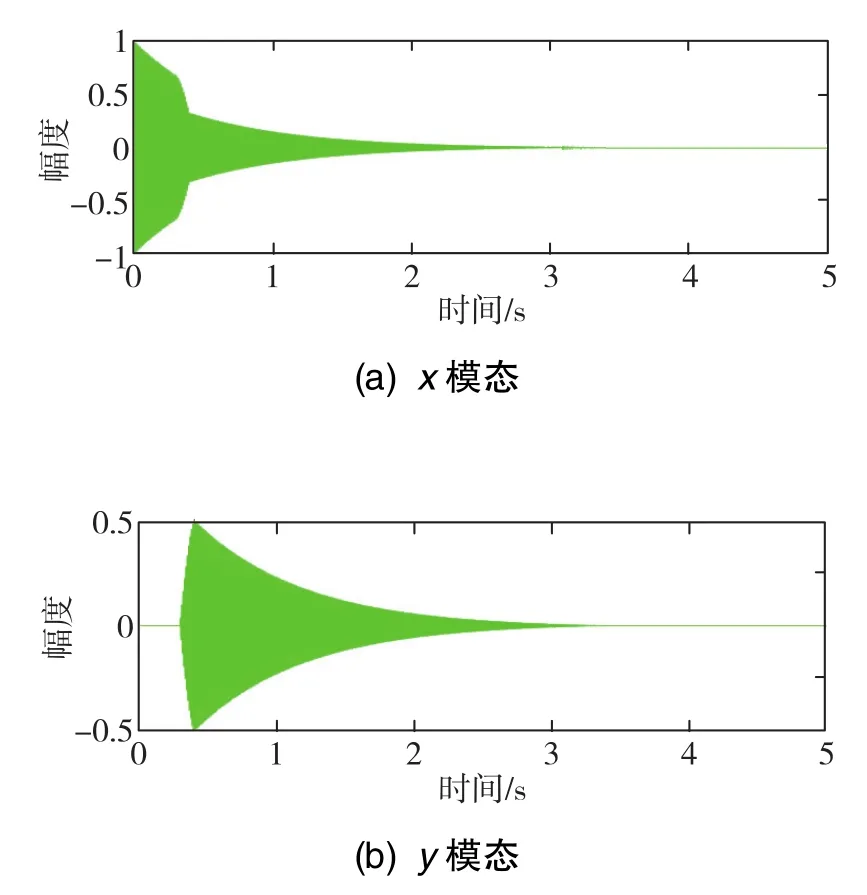
图3 存在对称阻尼情况下的陀螺模态时域响应图Fig.3 Time domain response diagram of gyroscope modal with symmetrical damping

其次被验证的是模态分裂效应。在Y轴谐振频率为99Hz的情况下,XY平面内的陀螺质心运动轨迹如图4所示。图4中,红点为当前质心,粉色虚线为最近的运动轨迹,蓝色曲线为历史运动轨迹。由图4可得,在x模态和y模态存在频率分裂的情况下,θ无法稳定在45°上,而是在平面内产生周期往复运动,这和之前的理论分析是一致的。图5表示的是将标称频率提高至200Hz的情况下,Y轴保持比标称频率低1Hz的运动轨迹图。在谐振频率提高的情况下,虽然系统依然产生周期运动,但是在同样时间内产生的漂移减小了。

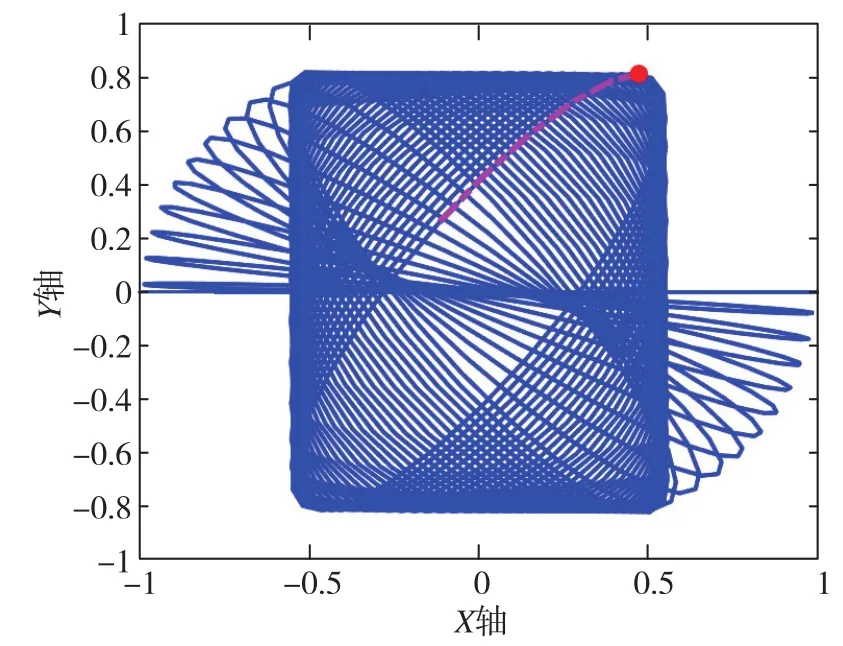
图4 谐振频率为100Hz、Δf为1Hz时，陀螺质心在XY平面的轨线图Fig.4 Trajectory diagram of gyroscope centroid in XY plane when f=100Hz and Δf=1Hz

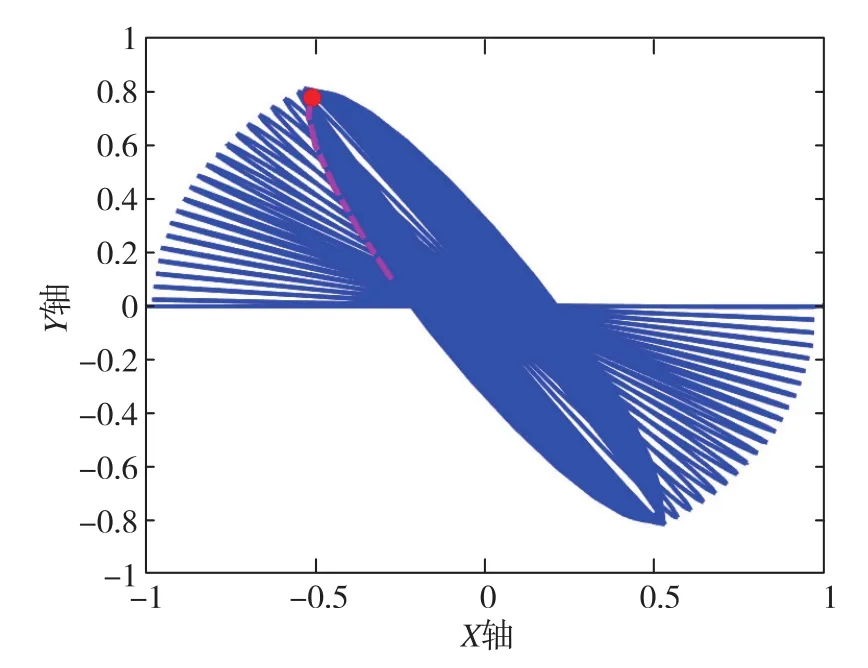
图5 谐振频率为200Hz、Δf为1Hz时，陀螺质心在XY平面的轨线图Fig.5 Trajectory diagram of gyroscope centroid in XY plane when f=200Hz and Δf=1Hz

随之被检验的是陀螺的阻尼不匹配问题,验证结果如图6、图7所示。由验证结果可知,当两个振动模态的阻尼不完全一致时,θ无法维持在原有角度,而是会漂移至衰减较小的轴线上。

在完成上述理论验证后,本文进行了控制系统的相关验证。在线式能量控制回路可以保证陀螺全角模式克服阻尼的作用,同时又不妨碍系统的自由响应模式。频率调谐和阻尼校正可在正式运行前进行一次性校正,其x模态和y模态的时域响应图如图8所示,在XY平面的运动轨线图如图9所示。由此结果可知,在控制系统有效的介入之后,陀螺的不理想因素得到了有效的抑制。在输入45°的Z轴物理旋转后,θ稳定在了同样的角度范围内并且随着时间而变化,系统能量无明显的衰减。

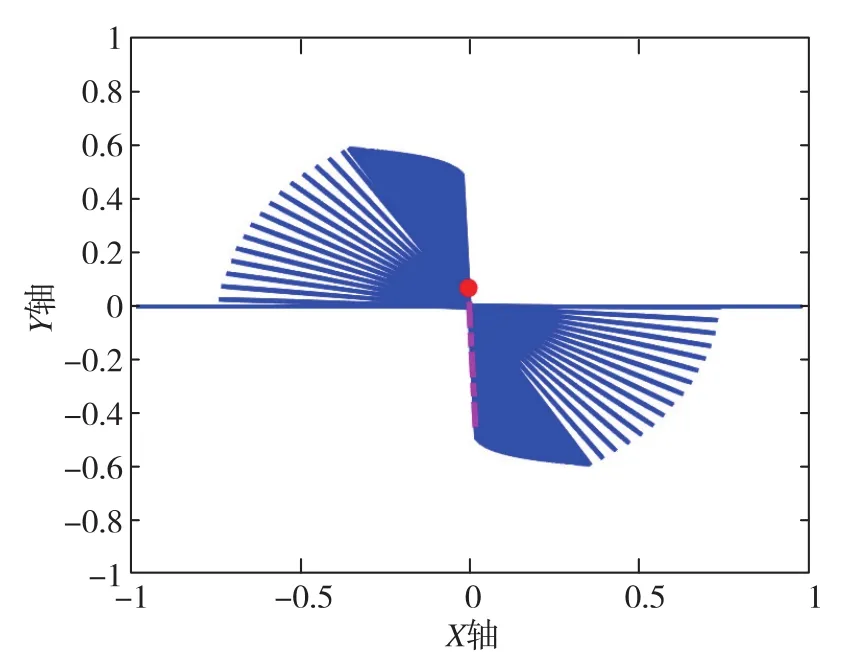
图6 Y轴阻尼较小时，陀螺质心在XY平面的轨线图Fig.6 Trajectory diagram of gyroscope centroid in XY plane when Y-axis damping is small

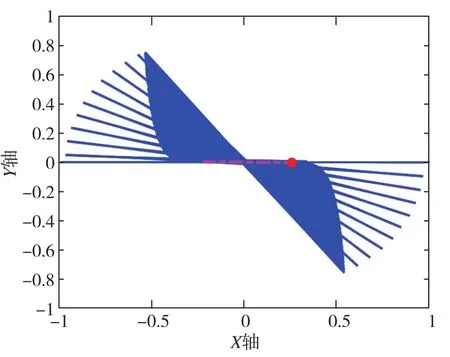
图7 X轴阻尼较小时，陀螺质心在XY平面的轨线图Fig.7 Trajectory diagram of gyroscope centroid in XY plane when X-axis damping is small

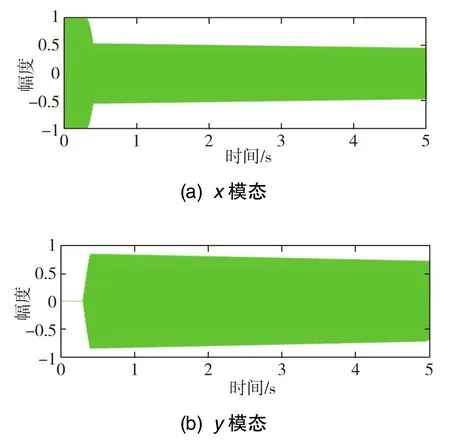
图8 控制系统校正后的陀螺模态时域响应图Fig.8 Time domain response diagram of gyroscope modal after control system correction

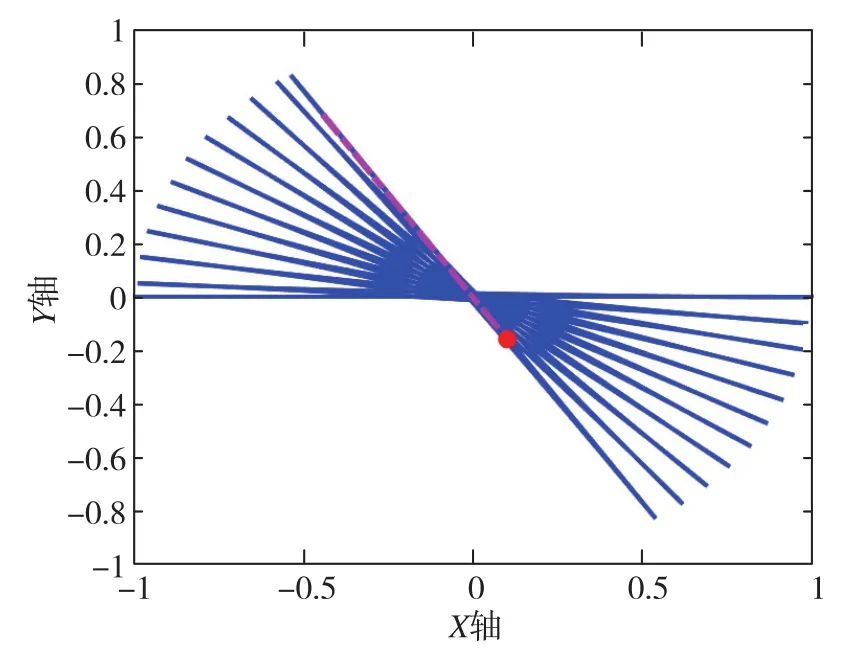
图9 控制系统校正后，陀螺质心在XY平面的轨线图Fig.9 Trajectory diagram of gyroscope centroid in XY plane after control system correction

5 结论

随着对陀螺直接测量角度和高带宽、高动态的需求,全角模式陀螺受到广泛关注。但由于全角模式对元器件对称性要求极高,各种不理想因素均会对全角模式的运行产生影响,其误差产生原理尚不明确,控制系统仍需进一步研究。因此,本文从谐振式陀螺全角模式的原理出发,深入研究了各种不理想因素对全角模式运行造成的问题。并针对各种不理想因素,从器件设计和控制系统校正两个方面提出了建议和解决方案。最后,利用Matlab的仿真结果验证了观点的正确性,并提出控制系统可有效解决相关误差因素。