基于热传导模型的高温作业专用服装设计

王婧琦 乔梦雪 刘艺航 肖亚美

摘   要：高温作业专用服装不仅适用于消防人员在火场的火焰区进行抢险救援，也可适用于玻璃、水泥、陶瓷等行业中的高温抢修时穿着。文章针对提供隔热保护专用服装的设计问题，结合相应数据建立环境温度随时间变化的热传导模型，利用偏微分方程边界值问题差分法对所建模型进行求解，进而确定高温作业专用服装厚度的最优设计。

關键词：高温作业服装;热传导;偏微分方程

1    问题分析

首先，利用Matlab仿真对附件数据进行处理得出皮肤温度随时间变化的曲线图。其次，通过对数据进行三阶拟合可得到假人皮肤温度与时间变化的函数关系为：

y=（9.1e?0.9）x3?（3e?0.5）x2+0.033x+37

再次，以第I层接触空气的点为原点，沿 II，III，IV，皮肤层方向为x轴建立坐标系，进而确定环境温度随时间变化的热传导数学模型，此模型分为高温作业下专用服装中的热传递模型与空气层中的热传递模型。

最后，利用偏微分方程边界值问题差分法对所建模型进行求解。

2    模型假设

（1）热防护服装的织物材料是各项同性的。

（2）系统热传递仅考虑热辐射、热传导的传热，忽略水汽、汗液的影响，即不考虑湿传递。

（3）厚度的测量的数值为精确值。

（4）假设假人都为成年男性，身高大约为170 cm。

3    模型建立与求解

3.1  数据预处理

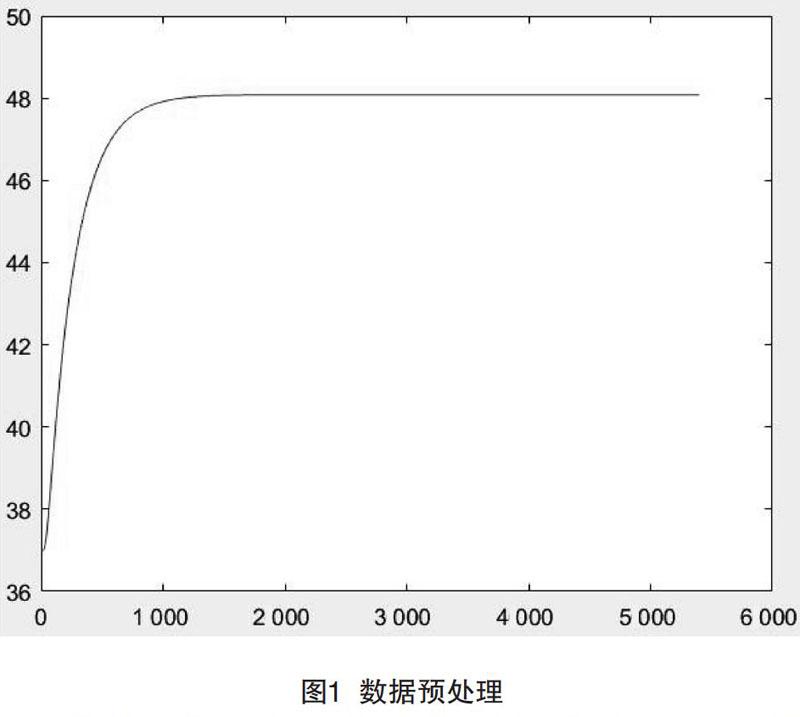
首先，利用Matlab仿真得出皮肤的温度与时间的拟合关系，从而建立起外界温度到假人皮肤之间所要经过的热传导模型。已知环境温度为75 ℃，90 min内实验数据的变化情况，且假人皮肤的初始温度为37 ℃，利用Matlab对数据进行描点绘图，数据预处理如图1所示。

通过观察图1可知在，1 736 s之后曲线平滑，没有明显上升趋势。之后对0 s和1 745 s之间的数据使用Matlab进行三阶拟合，得出拟合方程为：

y=9.1e?0.3×x3?3e?0.5×x2+0.033×x+37

此方程可表明皮肤温度与时间的函数关系。

3.2  高温作业下专用服装中的热传递模型

专用服装的实际应用中，本组主要考虑两种热传递形式，因为温差而引起的能量转移就是传热。在任何时候，只要在某个介质或者是两个介质之间存在温差，便会发生传热，这种传热即称为热传导，而辐射热也是造成受害者伤害的主要传热形式之一。

由于专用服装由3层植织物材料组成，即I层，II层和III层，I层厚度为0.6 mm，II层厚度为6 mm，III层厚度为3.6 mm，IV层为厚度5 mm的空气层。

基于以上假设，IV层和皮肤层可以近似看成只存在热传导。由此，3层的专用服装热传递模型[1]如下：

这里，，和分别是I层，II层和III层的显热容;T是温度;t是时间;x是水平坐标;KtcⅠ ，KtcⅡ和KtcⅢ的分别是I层，II层和III层热传导率;fL和fR分别是向外和向内的辐射量，Ωi表示关于x取值范围，i=1，2，3，4，5，texp是暴露在75 ℃环境中的时间。若采用常量将造成较大的误差结果。因此，在专用服装的热传递模型中，采用显热容法来描述织物的比热变化，同时，也反映了热化学反应过程的能量变化。

3.3  空气层中的热传递

由于空气层厚度狭小，可以将其看成一个矩形封闭腔，利用有限空间内传导/对流传热原理，综合考虑空气中传导/对流和织物辐射作用，由此，假定空气层的传导是稳态，辐射可以看成一种表面现象。根据假设，可以得到空气中的热传递模型如下：

因此，本文可以把上述空气层模型解耦成假定空气层中是稳态热传导和表面辐射传热，解耦后的空气层模型计算相对简单，实现效果良好，该模型被称为简单模型。

3.4  模型求解

由质量守恒和热量守恒定律可知，对高温作业服各层材料之间热传递产生的水蒸气浓度ωf，第3层材料与假人皮肤之间空气中水蒸气浓度ωa，以及材料温度T满足以下偏微分方程组[2]：

通过研究变量的关系，可以发现实验满足：

由此，可假设在温度变化范围内，同种，材料的吸收热量的能量不变，于是便得出微分方程组为：

使用有限差分法解决耦合偏微分方程组的定解问题，取4个整数N，m1，m2和m3，令时间步长为，织物3层对应的空间步长分别为：、和，则时间节点和空间节点分别为：

在第一层与第二层接触面，即当i=m1时有：

在第二层与第3层接触面，即当i=m1+m2时有：

综合考虑以上模型和数据拟合方程结果，利用Matlab仿真得到最终的温度区域分布，如图2所示。

根据专用服装每层温度随时间的变化趋势导出的数据绘制成曲线，如图3所示。

由图3可知，在初始温度为37 ℃的条件下，第一层温度会在外界高温的影响下发生骤变后保持温度恒定。第2，3，4层上升趋势大致相同，但因为材料的参数值不同，导致保持恒定温度的时间不同，恒定温度不同。第2层温度在37 ℃之后持续比例上升，第3层温度大约在37 ℃～57 ℃之间比例上升后保持57 ℃恒定，第4层温度在37 ℃～48.9 ℃之间比例上升后，保持48.9 ℃恒定[3]。

4    结语

本文针对温度环境考虑了热传递模型，在高温环境下纺织材料一些物理参数是随时间温度变化的，且这种变化对热传递有重要影响，同时，结合空气层提出了完整的热传递模型，更加贴近实际应用，对专用服装的安全性和舒适度提供了重要的参考数据。

[参考文献]

[1]潘斌.热防护服装热传递数学建模及参数决定反问题[D].杭州：浙江理工大学，2017.

[2]盧琳珍.多层热防护服装的热传递模型及参数最优决定[D].杭州：浙江理工大学，2018.

[3]李紫含，王世杰，徐伯乐，等.热防护服降温效果评价体系研究[J].武汉理工大学学报（信息与管理工程版），2018（1）：16-20.

Design of special garment for high temperature operation based on heat conduction model

Wang Jingqi， Qiao Mengxue， Liu Yihang， Xiao Yamei

（Henan Normal University， Xinxiang 453007， China）

Abstract：High temperature operation special clothing is not only suitable for fire personnel in the fire zone rescue， but also for glass， cement， ceramics and other industries in high temperature repair wear. Aiming at the design problem of special clothing for heat insulation protection， the heat conduction model of environment temperature changing with time is established based on the corresponding data， and the differential method of boundary value problem of partial differential equation is used to solve the model， so as to determine the optimal design of the thickness of special clothing for high temperature operation.

Key words：high temperature working clothes; heat conduction; partial differential equation