基于三维点云数据的花瓣形态及生长过程模拟

淮永建，杨丹琦，蔡东娜

基于三维点云数据的花瓣形态及生长过程模拟

淮永建，杨丹琦，蔡东娜

（北京林业大学信息学院，北京 100083）

目前对于虚拟植物的研究多是通过图形建模来模拟植物的生长变化，计算复杂且操作不灵活。随着三维扫描和点云重建技术的发展，为复杂植物形态可视化提供了新的手段。论文基于三维扫描的植物点云数据模型，研究了植物花瓣的形变和生长过程模拟。利用三维扫描仪获取植物花瓣的生长序列，采用MATLAB根据实测点云数据拟合植物生长函数曲线，最后将传统花卉生长模拟与点云模型的自由变形相融合，提出了依据实测点云数据通过点云模型变形算法模拟花卉植物动态生长的方法。该方法不仅能够保留花卉植物复杂的形态特征，而且使形变控制简单，模拟的花瓣形态及生长真实自然。此外，该方法还与基于物理的模拟方法进行比较，并利用拟合回归分析、实测花瓣数据与重建数据间误差对该方法的准确性进行了分析。结果显示花瓣生长期内决定系数达0.75以上及平均误差控制在2 mm以内，研究结果为花卉植物的生长形变模拟提供了参考。

三维；变形；模型；虚拟植物；点云；数据拟合；植物形变模拟

0 引 言

数字植物模拟是目前精准农林业信息化技术的研究热点。虚拟植物[1]具体是指应用计算机图形学模拟植物在三维空间中的生长、发育等过程，研究成果已被广泛应用于多个领域，在农林业、计算机动画、景观设计及计算机教学等领域都有着广泛的应用前景，特别是在生长过程研究和自然景观再现方面具有十分重大的意义。形态各异的植物器官代表了不同植物特有的属性，对植物的三维可视化建模具有重要的研究价值，其中花卉植物花苞开放过程模拟是植物生长过程模拟的难点。研究人员对虚拟花卉植物的研究多为基于曲面建模的形态结构模拟和基于L系统的生理结构模拟[2]，如秦培煜等[3]利用样条曲线曲面在控制点计算正确的前提下,虽然可以有效的绘制出植物的花瓣，并进一步组合静态植物花朵造型，但该方法却不适合控制伴随植物花朵开放过程中花瓣发生的连续弯曲形变。通过观察发现，植物形态在生长期间存在显著变化，由于这种过程固有的几何复杂性，在计算机图形学领域只有少数可以跟踪和模拟这种形态变化。其中，由局部的不均匀变化量所造成的卷曲形状叶子，前人曾推导出一个线性微分方程应变场来模拟叶片的收缩弯曲等现象[4]，但这些模拟方法非常复杂，无法精确验证。

正是由于植物器官形态相对迥异，且伴随着开放过程中花瓣等结构发生的卷曲形变情况，在原始手动建模的基础上很难实现较为逼真的模拟效果，因此，很多研究都选择避免这种复杂的生物模型，而是以直接跟踪扫描出的点云序列为基础，模拟现实的植物生长过程。

随着三维扫描技术的发展，在工业、军事、医学等行业应用的驱动下，人们越来越认识到三维扫描数据在几何重建方面的优越性，基于点云数据的曲面重构研究也成为目前计算机图形图像领域的研究热点。三维点云数据不仅能够精确记录物体表面的采样信息，而且能够全方位的记录场景信息，使场景的真实感更强。利用当前的三维扫描技术，本文通过收集花卉植物的形态数据以及不同时期的生长数据，为花卉植物生长模拟提供重要的数据依据与技术支持，并利用变形、曲面重建等技术较完整的再现花卉模型动态模拟生长的过程。点云模型[5]模拟花卉动态生长过程主要依据变形实现，其变形[6]的实质是点云模型在用户的控制下顶点发生改变，并在此基础上重构表面完成形状及位置变化。

针对提出的问题，此次研究主要目标如下：1）基于自由变形算法模拟花卉植物中花瓣结构的生长变化；2）使花瓣模型模拟生长变化更加真实，试验对大量点云数据做数据拟合，总结生长函数模型，使花瓣点云模型在实测数据的约束下完成变形效果[7]。

通过三维扫描得到花瓣模型数据，利用结合真实生长规律的自由变形技术，模拟随时间变化的花瓣造型序列，然后顺序演变模拟花瓣的动态生长过程。该方法直接作用于三维点云模型所嵌入的空间[8]，牵动内部模型发生形变，为虚拟植物生长模拟研究提供又一可行方案。

1 花瓣结构生长变形模拟算法设计

研究对象为三维仪器扫描[9]得到的花卉植物点云模型，与前人利用图形学技术建模的方法不同（无法直接控制模型自身形变）。为了实现模拟花卉模型的盛开效果，关键方法是将自由变形算法融合到模拟花卉植物生长的过程中。以往对于植物生长的模拟，如文献[3]是将变化过程简化为简单的几何形变，只追求形似，结果较为僵硬；如文献[7]则利用仪器追踪整个变化过程，致力于模拟逼真的变化过程，耗费大量计算时间，过程也相对复杂。本文为了使模拟过程与实测数据紧密联系且避免长时间追踪花卉变化过程，选择间断性的扫描花卉变化模型。从点云模型中提取样本数据，拟合符合真实花卉生长的变形规律，将传统模拟与实测数据相结合，本文主要方法如图1所示。

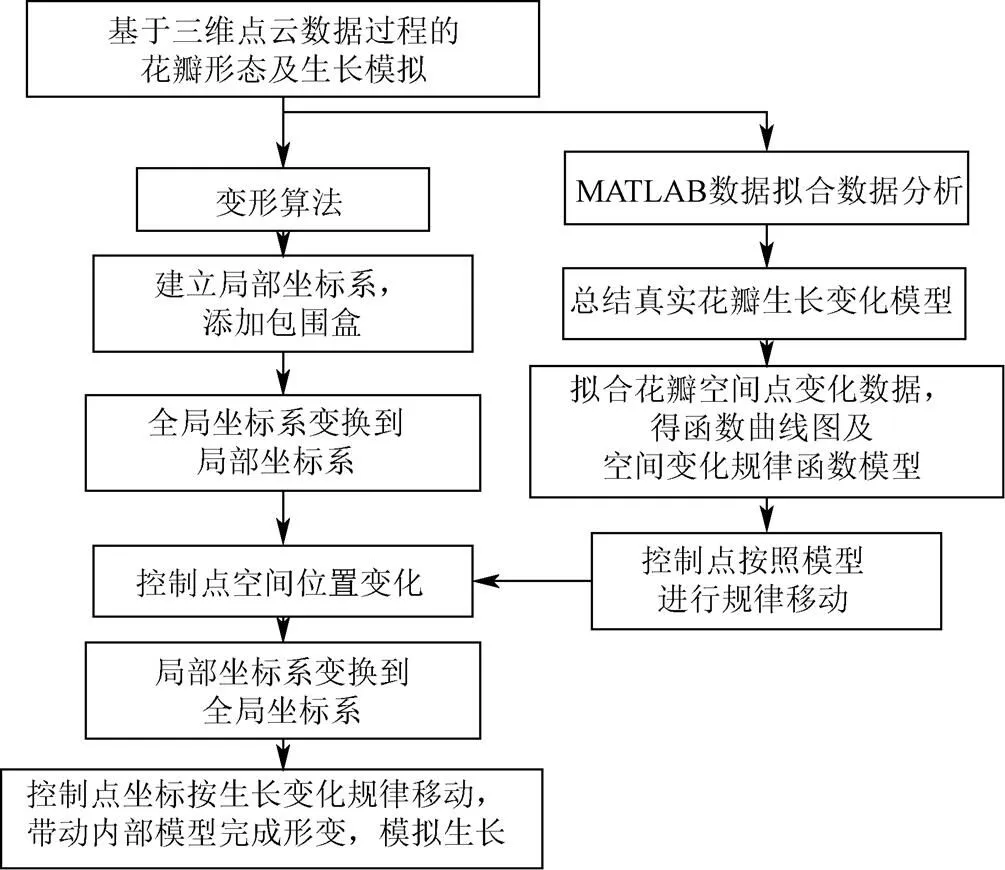
图1 花卉生长变形模拟算法流程图

2 相关理论

2.1 自由变形算法理论

自由变形算法首先由Sederberg和Parry[10]提出。传统自由变形算法表示，若物体所嵌入的变形空间被改变，则其中的物体也随之改变。因此，将变形物体嵌入一个框架中，当周围控制点位置改变时，该框架会带动内部模型伸缩扭曲[11]。

2.2 贝塞尔曲线

贝塞尔曲线[12]所包含的性质与自由变形思想最为契合。其中传统花卉植物模拟多是利用曲线曲面构建模型形态结构，如B样条曲线曲面和得到进一步推广的非均匀有理B样条曲线曲面（NURBS曲线曲面）[13]。通过设定控制点个数、节点数和阶数构造曲线曲面模型，进而对模型实现更精确的控制，而且通过改变少量的控制点位置就可以完成模型不同造型的设计，进一步构建出不同花朵造型。传统通过控制点构造曲线曲面的花瓣模型[14]，如图2所示。

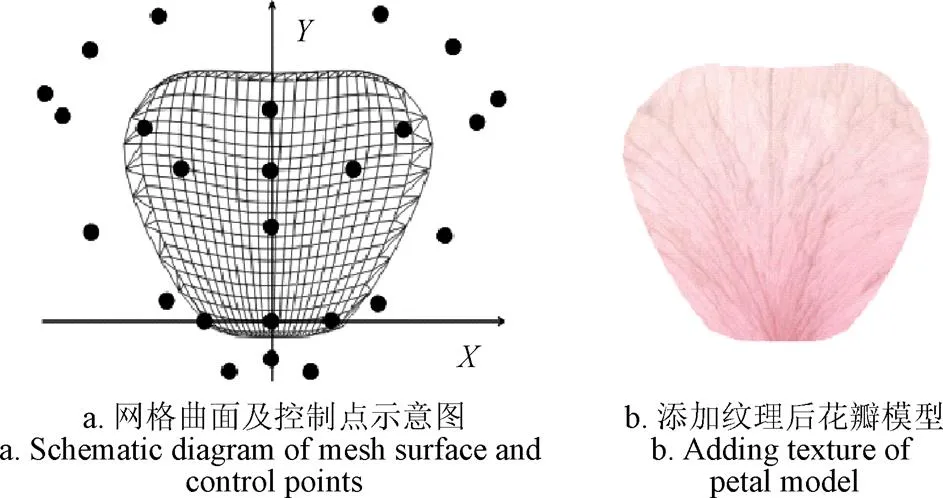
图2 传统花卉结构模型

在传统曲线曲面建模过程中当控制点增加时，曲线变得不可控，其动态变化的连续性也会变差，且植物细节特征无法准确体现出来，模型真实感较弱。因此，传统方法并不适合花瓣在开花过程中的连续弯曲形变模拟。

贝塞尔曲线中“关键点可以控制曲线弯曲”的性质可以准确运用到自由变形思想中，只需将待变形物体看作是构造曲面时的一个体，三维贝塞尔曲线同样可以通过控制外部关键点，改变内部物体的形状[15]。

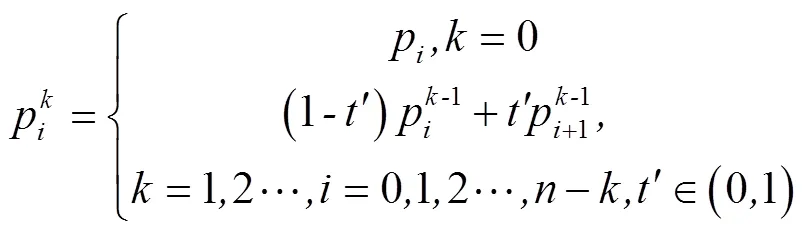
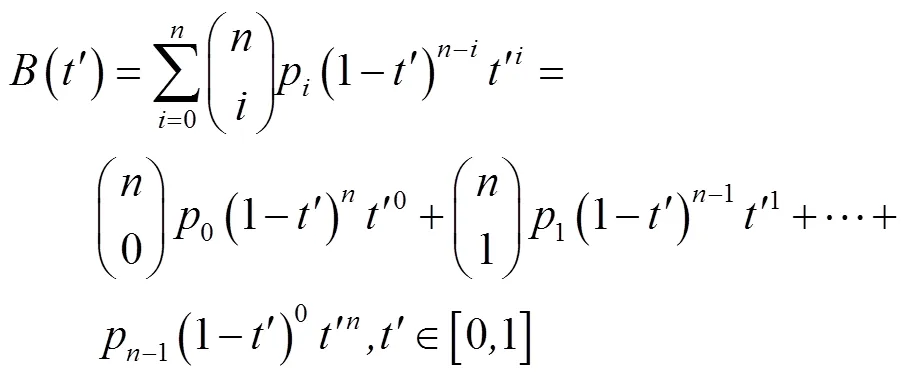
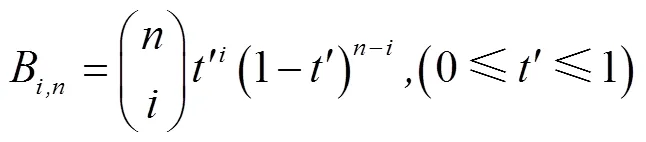
3 自由变形算法中空间点坐标变换

3.1 空间点局部坐标

在模型变形过程中为了方便控制点坐标间转换，使控制点的世界坐标无论怎样变化都存在固定不变的局部坐标（,,）参与运算，需要构造一个局部坐标系[17]，如图3所示。

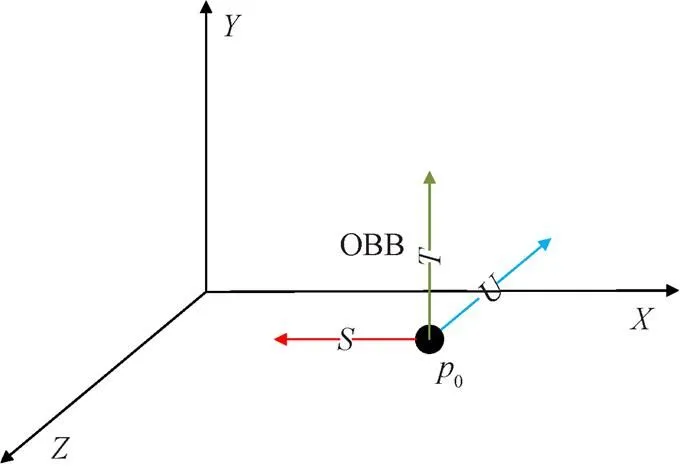
图3 局部坐标系

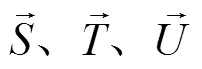
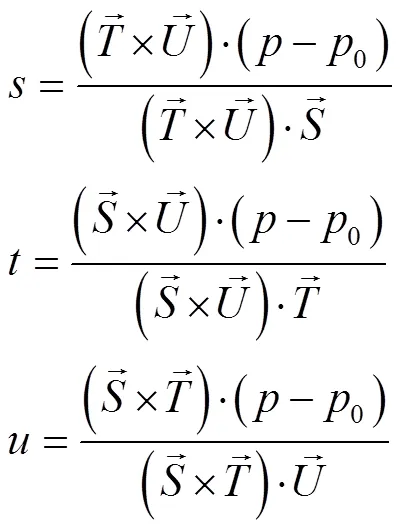
3.2 空间点坐标转换

模型添加的OBB外部包围盒上控制点（即划分网格顶点）坐标为局部坐标，本文为实现前文讲述的坐标变换过程，需将局部坐标转换为世界坐标进行运算，为了实现该过程本文设计如下算法。

算法1 空间点坐标转换算法

输入：有mesh结构（顶点坐标数组Vector3[] vertices，以及通过顶点为网格创建三角形面片int[] triangles）的模型对象。

输出：为模型添加OBB包围盒并计算网格顶点世界坐标；

1）初始化模型网格结构mesh。

2）利用mesh结构中边界的最大值与最小值的差值计算模型包围盒边界最远距离max, 并得出对应的横、纵、竖坐标轴及原点信息0。

3）将模型分横、纵、竖坐标划分网格m_customDivide[0]、[1]、[2]。

4）计算网格顶点局部坐标（：分别为横，纵，竖坐标轴方向上网格顶点循环计数）。

5）利用矩阵运算将局部坐标转换为世界坐标。

3.3 模型顶点更新

当控制点坐标发生变化后，将函数从二维平面拓展至三维空间，新的模型顶点坐标需要未改变时模型顶点的局部坐标、改变后控制点的世界坐标以及Bernstein多项式的值[19]共同参与运算得出，计算新模型顶点坐标(,,)，如式（5）所示

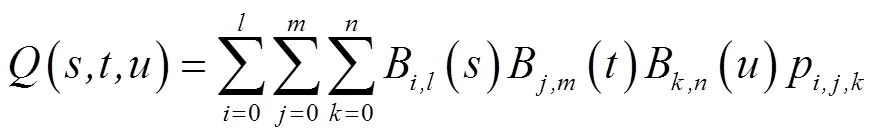
式中,,分别为STU坐标轴方向上划分的网格数，p,j,k为控制点更新后的世界坐标（为循环计数），为Bernstein多项式系数，公式右侧括号中,,分别表示改变前模型顶点局部坐标。

4 基于点云数据的生长函数拟合

传统模拟植物花卉生长或植物物质积累量化过程通常会利用Logistic回归模型[20]，本文在传统生长函数的基础上结合前期扫描得到的点云数据模型[21]，提出了一种拟合实际样本数据的植物生长模拟方法。从花卉采集的生长序列数据中得出花瓣生长变化规律，在模拟花卉盛开时将生长函数引入控制点变化过程，从而实现生长模拟。

4.1 点云数据处理

根据试验条件，前期在花卉生长的不同时期扫描花瓣模型，通过相同扫描方式、相同位置摆放，扫描得到6个不同生长时期花卉整株模型，在花卉模型中提取花瓣，选取扫描结果相对完整的花瓣作为数据采集样本。花瓣点云数据处理方法主要流程如图4所示。

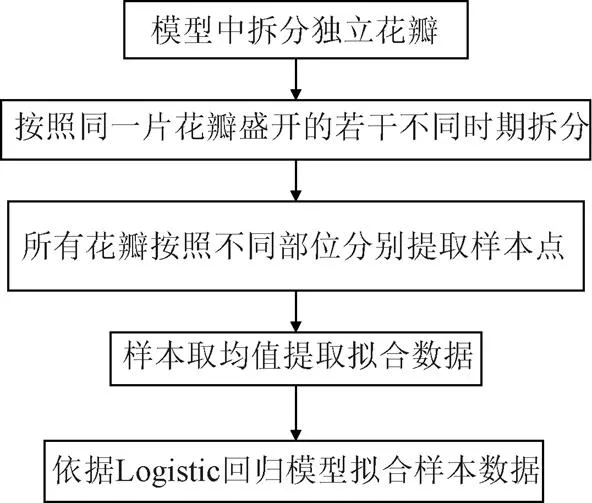
图4 数据处理方法

步骤1：从整朵花模型中拆分出独立花瓣，如图5所示，该过程使用到Meshmixer中切割模型转换为零件的功能[22]，将扫描模型中每一时期的每一瓣花瓣拆解出来并按照原本的拓扑结构输出得到样本模型。图5a为使用工具拆分模型后的输出结果，不同颜色表示拆分后不同部分并且拓扑结构保留，图5b～5d则展示了同一片花瓣点云模型不同时期的变化。

步骤2：由于花瓣模型点云数据量较大，即使同一片花瓣不同部分的变化规律也各有不同，为了使拟合的生长函数更具有普遍性，采取的方法是将同一片花瓣分割成生长特点各不相同的若干部分分别采样，利用MeshLab切割模型功能，将每部分点云数据（即点的坐标信息）输出作为样本数据，如图6所示；由于每种花卉植物的花瓣、叶片结构都各有不同，因此可以针对具体形状做不同的分割方式。

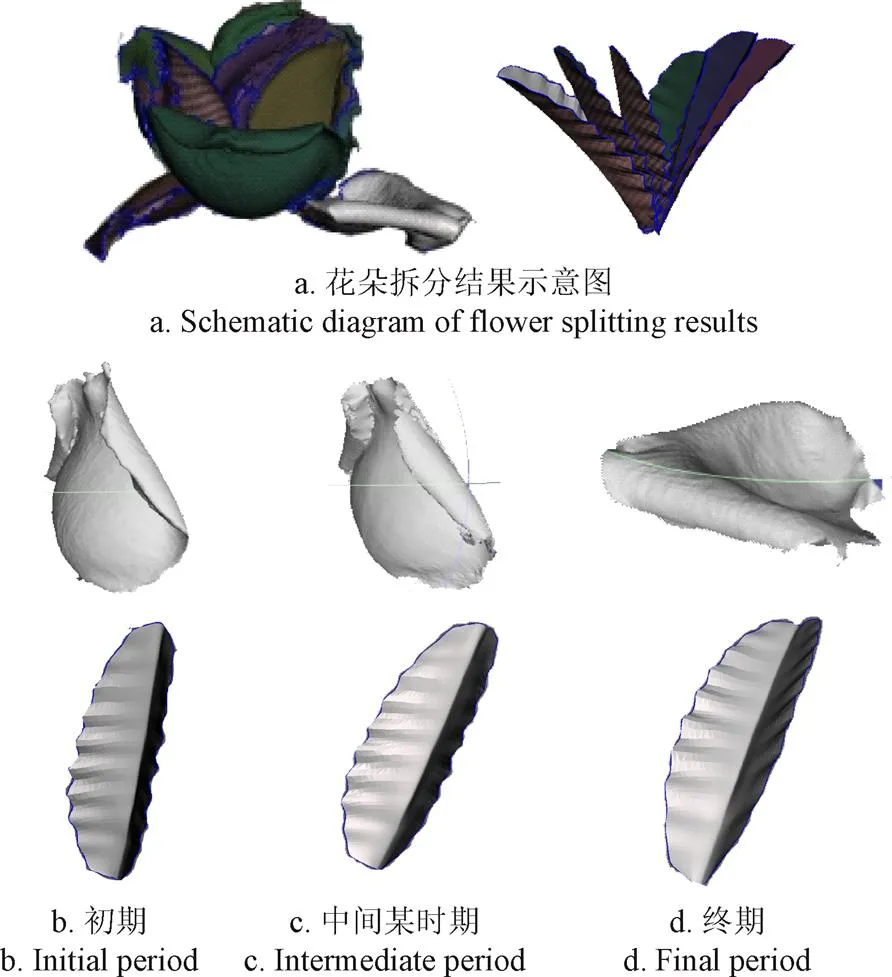
图5 花瓣拆分示意图

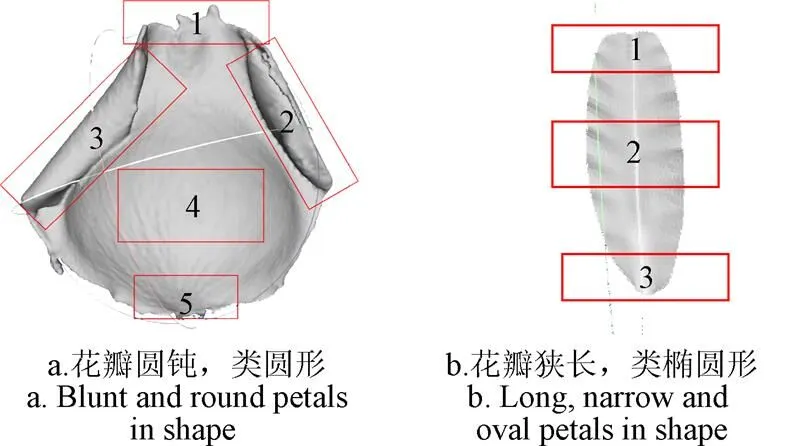
注：左侧花瓣（1－5），右侧花瓣（1－3）分别表示花瓣不同分割部位。

步骤3：利用MATLAB中cftool工具[23]对采样数据拟合，采用给定函数形式的拟合方式构造生长函数模型。MATLAB数据拟合的基本原理是最小二乘法原理[24]，该方法对于非线性数据可以通过简单的变量变换使之线性化，这样便可求出参数变换后的函数方程[25]。

4.2 数据拟合

花瓣空间位置随时间的变化规律需要不同时期花瓣的形态及位置信息。在本次试验中由于三维扫描仪只能扫描植物外围信息，其中遮挡会使内部信息产生缺失，因此为了简化试验，选取了同一朵花卉模型中每一时期扫描结果都相对完整的同一片花瓣为研究基础，选取少量样本数据验证方法的有效性。

样本数据处理中每一时期的花瓣模型均被分割为生长特征各不相同的若干部分，其中每部分信息均包含横、纵、竖坐标的空间点云数据。此外，为了方便函数拟合，需要将每一时期花瓣的点信息整合为一个单独的随时间变化的变量，因此，在之后的数据处理过程中将得到的坐标点分横、纵、竖坐标求取均值解决[26]。

数据拟合[27]采用MATLAB中给定函数形式的拟合方法。拟合过程中，生长函数拟合选取常用的Logistic回归模型[28]，将处理得到的数据与该函数模型相结合拟合出符合真实采样数据的生长变化函数，为变形算法提供数学依据，函数模型如式（6）所示：

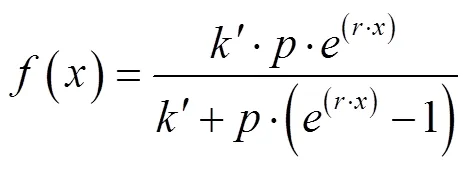
式中表示终止状态参数，p表示初始状态参数，r表示函数随自变量的变化速度，自变量x为时间（d），函数f(x)表示花瓣生长随时间的变化规律。以试验中月季及君子兰6个时期样本点数据拟合为例，生长曲线如图7所示。

4.3 结果分析

根据不同时期数据拟合的生长函数模型结果可以得出，真实样本数据与传统Logistic回归模型的拟合度较高，基本上呈前期生长速度较快，速度逐渐减缓的生长规律。

5 基于生长函数的自由变形算法实现

传统模拟花卉植物生长常通过构造曲线曲面模拟花瓣、花蕊等形态结构特征；另外采用L系统文法表达花卉植物，将理想环境下的动态生长函数引入到花瓣形变过程中，通过控制花瓣旋转角度，卷曲程度等因素构造不同时期花瓣形态，形成基于L系统的花朵动态开放过程[29]。本文为了实现模拟花瓣动态生长过程采用了便于控制的三维点云模型变形算法，跟传统方法相比，本方法对模型的形变操作更加便利，且具有更自然的变形效果。如何将传统自由变形算法与模拟花瓣生长变化相结合是本文的关键所在。而传统FFD自由变形算法通常运用在相关三维模型的形变上，如刚体打击变形、赛车车体变形[30]等，将FFD运用于植物生长模拟还没有过多研究。本文主要研究了结合生长函数模型的自由变形算法模拟花瓣生长形变的问题。

由变形原理可知，为使花瓣模型按照真实生长规律发生形变，将生长函数模型（6）引入式（5）中控制点p的运动过程，为控制点的变化加以约束，使其在既定轨迹上进行变形。该方法既保持了花瓣结构的原始特征，又与实测生长数据相结合。通过添加包围盒上控制点的轨迹约束，牵动内部模型按照外部包围盒的变化而发生形变，实现花瓣模型变形模拟生长的过程。具体算法设计如下：

算法2 模拟花瓣结构生长变形算法实现

输入：待形变模型，包括模型相关点、线。

输出：更新顶点坐标后模型。

1）按横、纵、竖坐标划分模型网格数。

2）获取花瓣模型起始坐标点（：网格顶点循环计数）。

3）获取花瓣模型终止坐标点。

4）变化过程中结合生长函数更新控制点，，为拟合函数参数，为形变速度，为时间(d)。

5）计算伯恩斯坦系数，如式（3）所示。

6）计算更新后模型顶点坐标（为模型顶点循环计数；为控制点局部坐标；，，分别为横、纵、竖坐标划分总数；，，分别为横、纵，竖坐标方向上循环计数）。

7）根据更新后模型顶点坐标重建模型表面三角面片，实现变形。

6 试验结果与分析

本文基于点云模型自由变形方式实现了花瓣从初始状态变化为盛开状态的动态生长过程。在试验中，为了使生长变形效果可以清晰地展示出来，将起始形态花瓣与终止形态花瓣添加了根底部位置约束，即事前将花瓣底部位置对齐，使花瓣的变形效果得以比较，如图8所示。变形过程中，花瓣的具体形变效果如图9所示，与现实中月季等重瓣花和君子兰兰科的变形效果类似，前期花瓣卷曲程度较大，随时间变化花瓣逐渐舒展，卷曲程度减弱，并向外扩展，角度与位置也发生相应变化，生长主要呈扩大、向外舒展的趋势。运用本文提出的基于点云模型变形的方法较好实现了花瓣生长模拟效果，模拟了花瓣在生长过程中的空间位置以及形态结构变化规律。

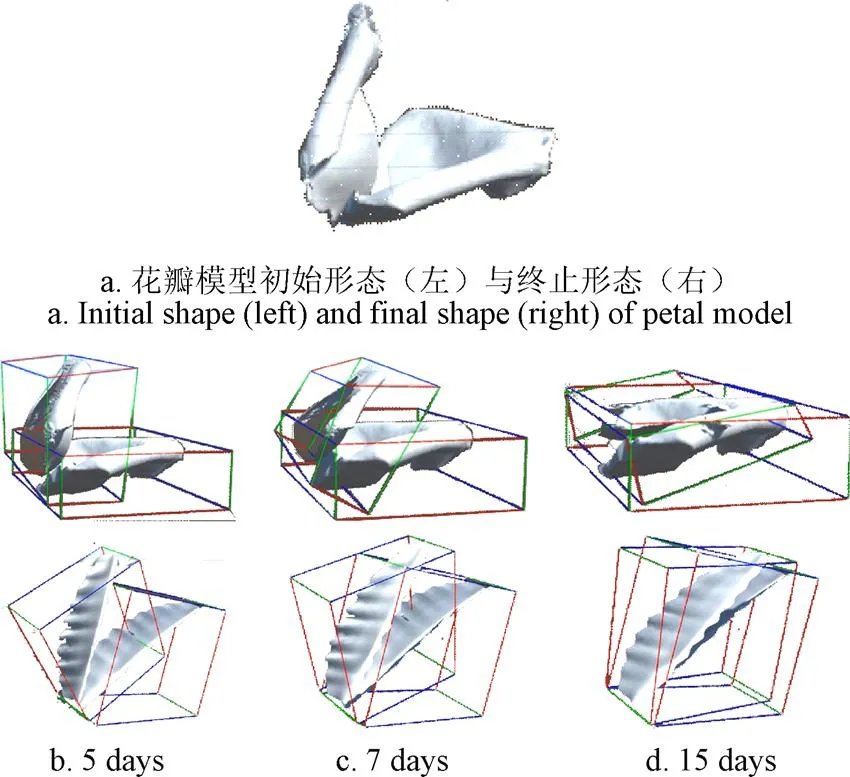
注：上层为月季，下层为君子兰，左侧为变化花瓣，右侧为终止时期对比花瓣。

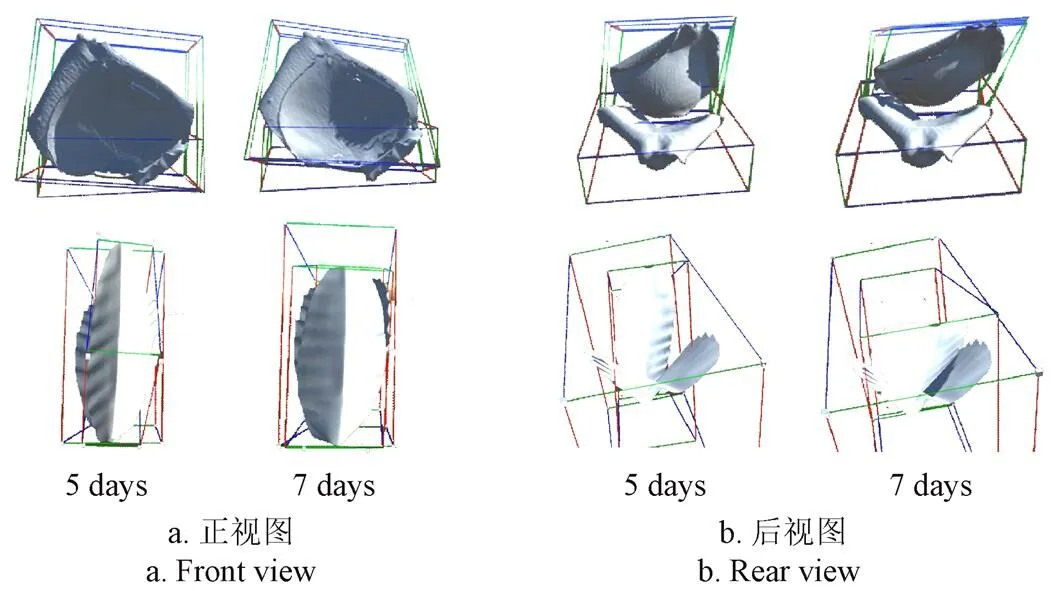
注：上层为月季，下层为君子兰。

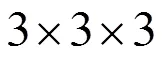
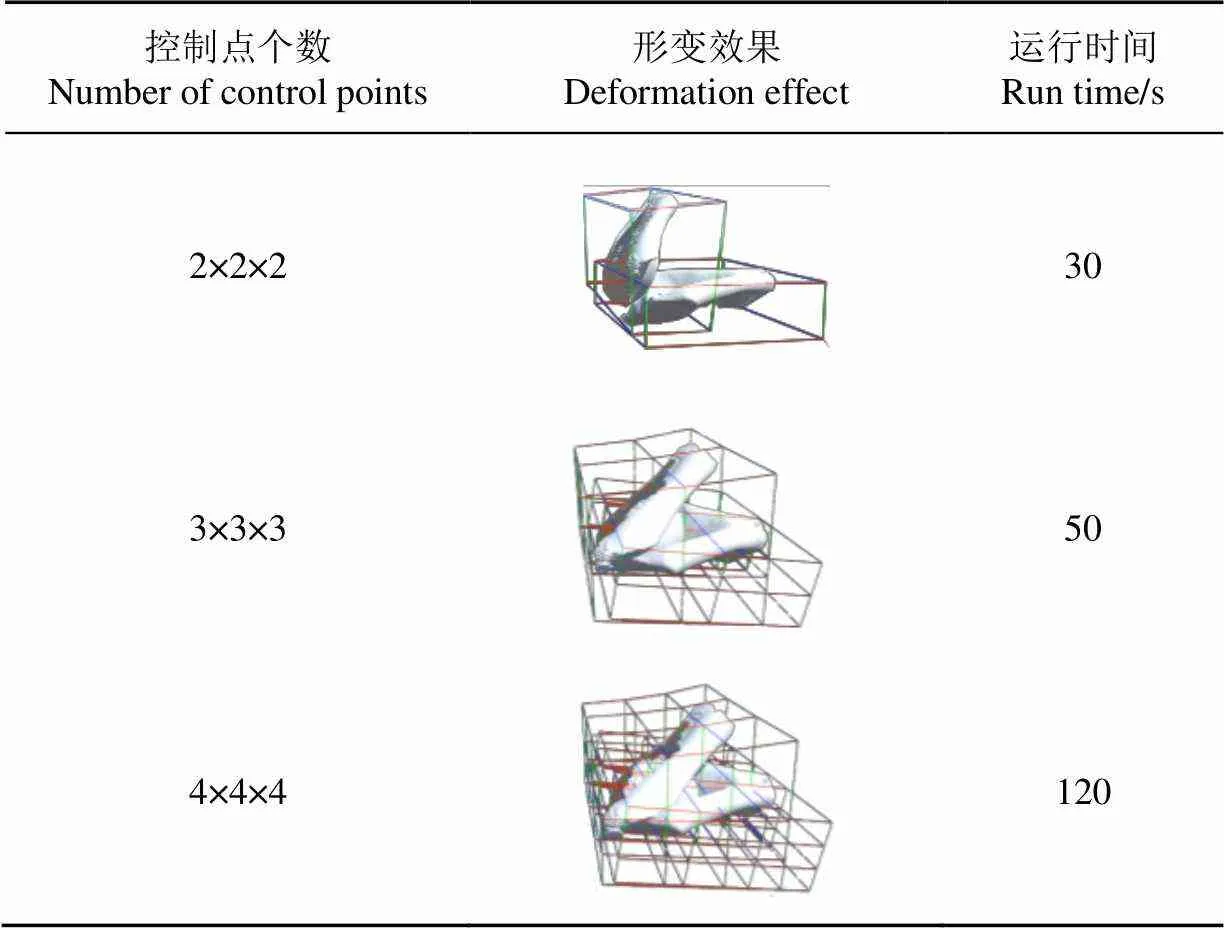
表1 控制点个数与算法效率关系

实现花朵整体生长模拟采用的方法是将每片花瓣根据本文的变形算法从初始状态（即花蕾时期）生长变形为终止状态（即完全盛开时期），具体形变过程如图10，图11所示。此次研究并不涉及花瓣结构的枯萎过程和花蕊生长模拟，此外，为了显示完整花瓣造型，在试验过程中对模型进行了简单渲染。

为了验证数据拟合以及模拟生长变形方法的实用性和鲁棒性，试验中扫描并处理了多种花卉植物进行模拟，并将重点放在不同大小、形状和复杂度的花朵上。如表2所示，为试验过程中各种花卉的生长函数拟合参数值（,,）以及衡量拟合优度的指标2（决定系数）。根据回归分析的性质可得，2值基本保持在0.75以上说明数据能够较好拟合函数模型，得出的参数值能较好的表示数据的变化规律，结果表明本文的数据采集和数据拟合方法符合实际与理论基础。

图10a中将本文方法与基于物理的开花模拟方法[31]进行了比较。同样针对重瓣花植物（本文利用月季而对比文献为梅花）做开花模拟对比。虽然纯物理建模结果具有简单和对称性的特点，但是依据点云模型变形的方法利用了花卉植物生长的真实数据，使生成的花开动画更加逼真且更具有通用性。如图10b所示，较好重建了花卉盛开后形态。

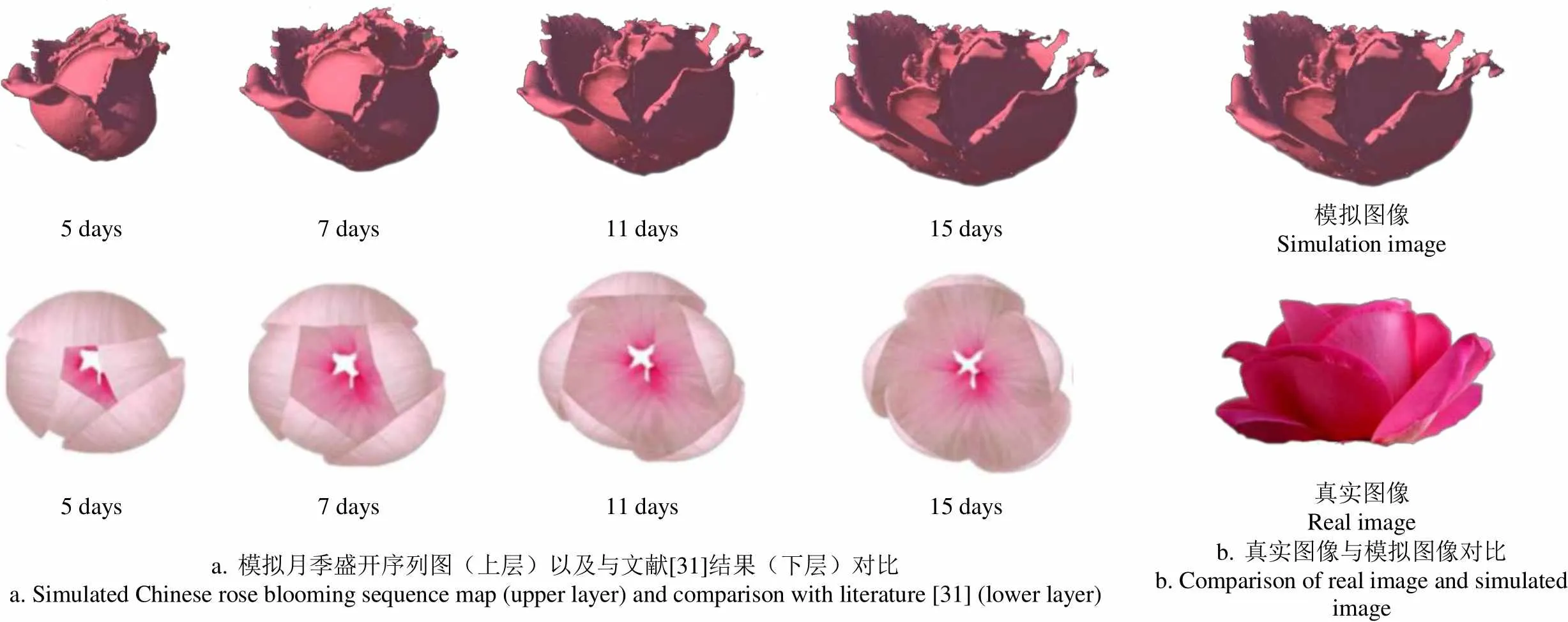
5 days7 days11 days15 days模拟图像Simulation image 5 days7 days11 days15 days真实图像Real image a. 模拟月季盛开序列图（上层）以及与文献[31]结果（下层）对比a. Simulated Chinese rose blooming sequence map (upper layer) and comparison with literature [31] (lower layer)b. 真实图像与模拟图像对比b. Comparison of real image and simulated image

表2 不同类型花瓣的拟合参数及拟合优度分析

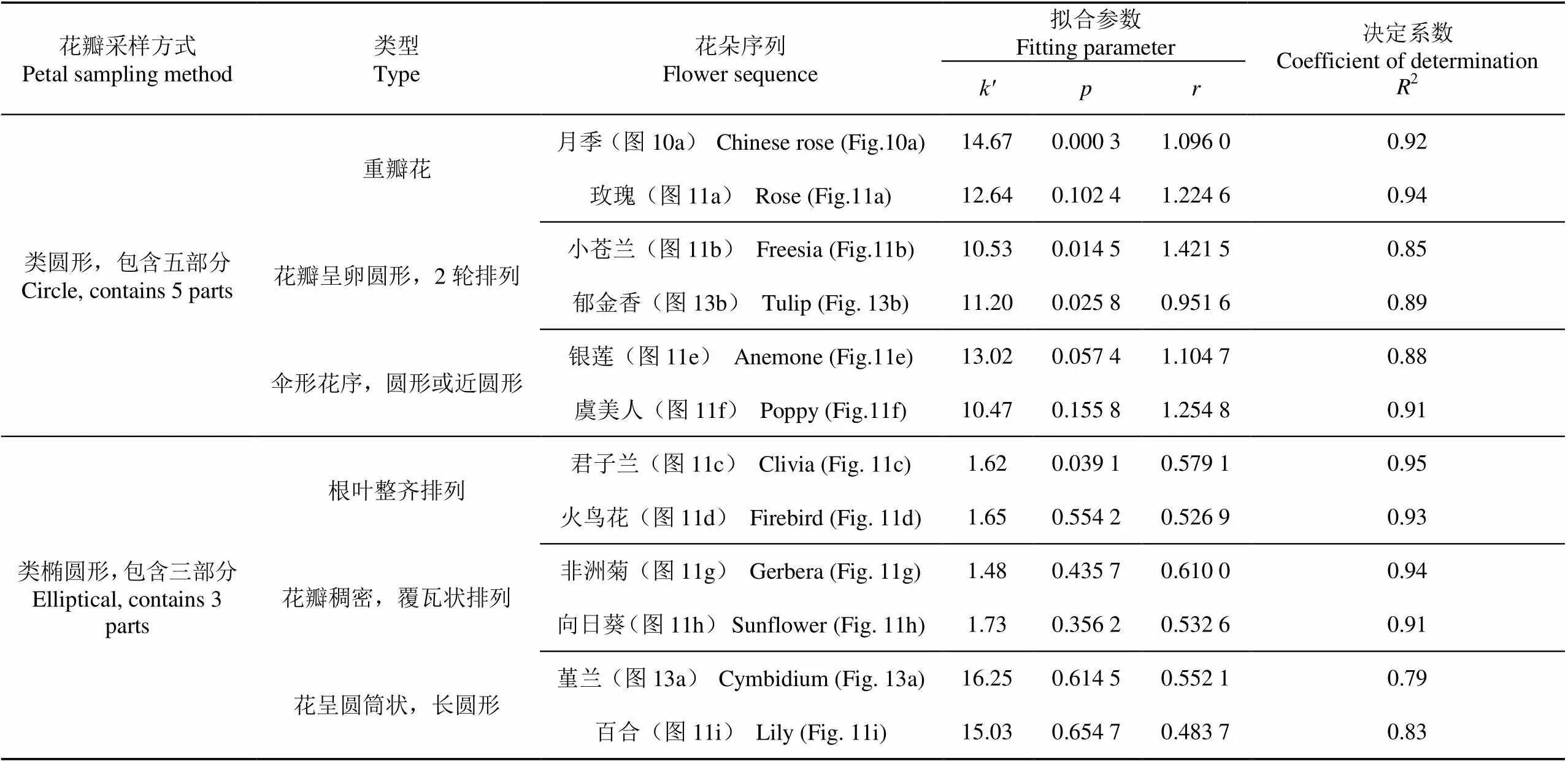
Table 2 Fitting parameters for different types of flower and goodness of fit analysis

利用本文提出方法，只需提供花卉植物初始点云模型和终止点云数据，添加变形函数后便可将花卉盛开过程的中间序列逐一重现出来。如图11所示，截取各类花卉盛开过程中4个时期展示模拟效果。从变形重建结果与扫描真实点云模型重建结果对比可以看出，该方法能较真实模拟植物生长的不同阶段，针对月季等花瓣相互重叠（如图10a）、向日葵花瓣繁多且互相交错排列（如图11h）、以及百合花瓣较大弯曲明显（如图11i）等特征的花卉植物也有较好模拟效果。该方法保留了植物真实细节特征，如图10中花瓣的实际卷曲效果和真实拓扑结构，而以往通过图形学方法无法真实重现。但是，由于三维扫描仪器只能获取植物外层可见信息，植物内部重新生长或没有完整扫描的结构无法得到有效模拟。

图11 不同花卉种类模拟花瓣开花序列及点云数据重建模型对比

为了定量有效评价运用本文方法后的模拟精度，我们计算了重建表面与原始测量数据之间的误差，并对比了动态开花过程重建表面与阶段扫描结果之间差异的变化情况。误差度量定义为三维空间中沿，，方向上每片花瓣的真实测量值与变形重建后测量值之间差值的平均值。如图12所示，所有花卉的重建误差基本都在2 mm以内，与花瓣的典型尺寸相比（50～150 mm），误差相对较小；百合等花瓣形状较长的花卉重建精度相对较低，是因为它的尺寸较大且生长后期卷曲程度加大的原因。由此，本文运用真实点云数据拟合的生长规律以及模拟生长形变的方法，很好地再现了植物的生长过程，最终重建的植物模型与真实生长植物具有较高的相似度。

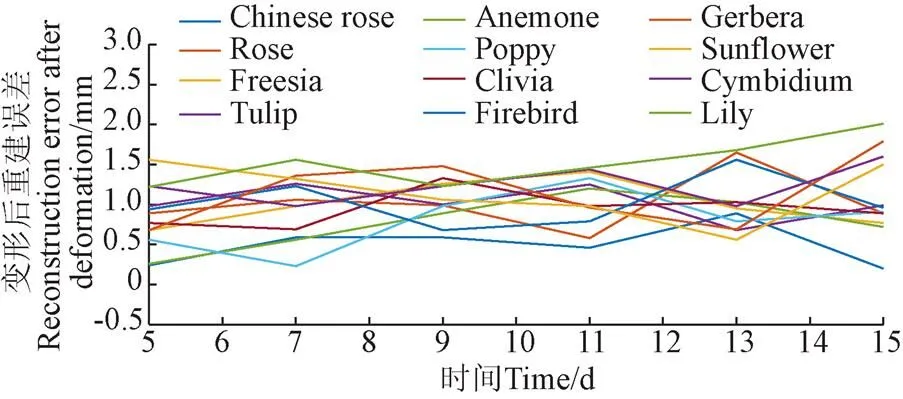
图12 不同花卉种类模拟开花过程中重建误差

本文模拟花卉生长形变的方法，不仅适用于试验中花卉点云模型，而且还为不同花瓣提供生长信息，使某一种花卉的开花运动特征可以被提取并转移到另一种花卉植物上。如图13a所示，为堇兰结合百合生长规律后生长变形效果。还可将郁金香单层生长规律叠加至双层，即内层与外层采用同种形变规律，形成整株花卉的开花模拟效果，如图13b所示。

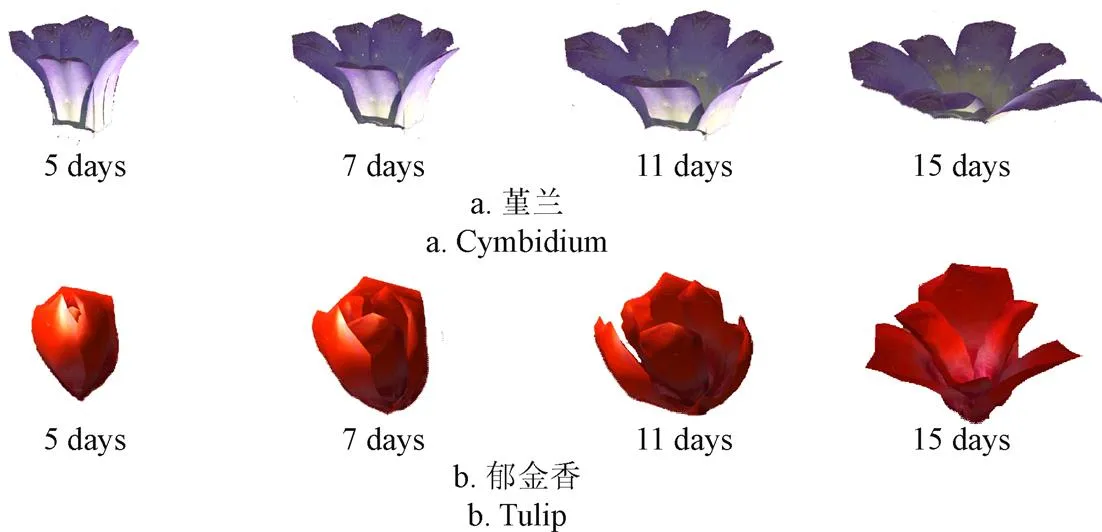
图13 花卉生长规律的应用

7 结 论

本文主要研究了基于三维扫描点云数据拟合生长函数规律有效模拟花瓣结构生长形变的问题。该方法克服了传统模拟植物生长过程中前期需要进行复杂三维建模的过程。利用三维扫描技术使植物形态结构更加逼真，且与实测数据相结合使花卉生长过程更加真实。利用自由变形算法，通过调节模型包围盒上控制点使花卉模型形变自然；利用不同生长期点云模型的生长函数拟合，对控制点空间位置进行约束形变，从而真实模拟植物的生长序列，达到模拟与仿真相统一的目的。函数拟合结果经回归分析后决定系数2>0.75，说明本文采集数据拟合生长函数方法的有效性；误差分析中误差值<2 mm，则说明本文提出的利用自由变形算法模拟不同形状、复杂度花卉生长序列方法的适用性。研究结果表明，结合真实生长函数的自由变形算法能较好模拟花瓣结构的生长形变。

本文方法在追求实时形变的前提下舍弃了部分变形精度，因此该方法仍然局限于形状和结构相对简单的阔叶类花卉植物模型形变模拟。未来的工作计划将本文算法扩展到复杂植物种类的变形中，通过改善算法使点云模型的变形效果更加明显高效。

[1] Owens A, Cieslak M, Hart J, et al. Modeling dense inflorescences [J]. ACM Transactions on Graphics (TOG), 2016, 35(4): 1－14.

[2] Prusinkiewicz P, Cieslak M, Ferraro P, et al. Modeling Plant Development with L-Systems [J]. Mathematical Modelling in Plant Biology, 2018: 139－169.

[3] 秦培煜，陈传波，吕泽华. 利用 L-系统和 Bezier 曲面的植物花朵模拟模型[J]. 计算机工程与应用，2006，42(16)：6－8.

Qin Peiyu, Chen Chuanbo, Lü Zehua. Plant flower simulation model using L-system and Bezier surface[J]. Computer Engineering and Applications, 2006, 42(16): 6－8. (in Chinese with English abstract)

[4] Xiao H, Chen X. Modeling and simulation of curled dry leaves [J]. Soft Matter, 2011, 7(22): 10794－10802.

[5] Thanou D. Graph based compression of dynamic 3 D point cloud sequences[J]. Transactions of the Chinese Society of Agricultural Engineering ( Transactions of the CSAE), 2016, 25(4): 1765－1778.

[6] 张湘玉，李明，马希青. 基于细分的网格模型骨架驱动变形技术[J]. 计算机应用，2015，35(3)：811－815.

Zhang Xiangyu, Li Ming, Ma Xiqing. Skeleton-driven deformation technology based on subdivision mesh model[J]. Journal of Computer Applications, 2015, 35(3): 811－815. (in Chinese with English abstract)

[7] Zheng Q, Fan X, Gong M, et al.4D reconstruction of blooming flowers [J]. Computer Graphics Forum. 2017, 36(6): 405－417.

[8] Vereecken H, Schnepf A, Hopmans J W, et al. Modeling soil processes: key challenges and new perspectives[J]. Vadose Zone Journal, 2016,15(5): 1－120.

[9] 杨亚飞，张定华，黄魁东，等. 基于椭球包围盒的锥束三维加权重建算法[J]. 仪器仪表学报，2016，37(11)：2563－2571.

Yang Yafei, Zhang Dinghua, Huang Kuidong, et al. Three-dimensional weighted reconstruction algorithm of cone beam CT based on ellipsoidal bounding box[J]. Chinese Journal of Scientific Instrument, 2016, 37(11): 2563－2571. (in Chinese with English abstract)

[10] Sederberg T W, Parry S R. Free-form deformation of solid geometric models [J]. ACM SIGGRAPH Computer Graphics, 1986, 20(4): 151－160.

[11] 詹杭龙，刘澜涛，康亮环，等. 一种基于模型的弹性可伸缩的流处理框架[J]. 计算机研究与发展，2017，54(5)：1086－1096.

Zhan Hanglong, Liu Lantao, Kang Lianghuan, et al. An elastic scalable flow processing framework based on actor model [J]. Journal of Computer Research and Development, 2017, 54(5): 1086－1096. (in Chinese with English abstract)

[12] Penner A. Odf using a cubic bézier[M]. Fitting Splines to a Parametric Function. Cham, Springer, 2019: 19－26.

[13] 孙思，葛卫民，冯志勇，等. 基于NURBS变形和单视角图片的人脸表情生成[J]. 计算机工程，2017，43(11)：227－233，238.

Sun Si, Ge Weimin, Feng Zhiyong, et al. Face expression generation based on NURBS deformation and single view image[J]. Computer Engineering, 2017, 43(11): 227－233, 238. (in Chinese with English abstract)

[14] 淮永建，周文婷. 基于重瓣花朵拓扑结构模型算法的可视化研究[J]. 计算机科学，2012，39(9)：282－283.

Huai Yongjian, Zhou Wenting. Visualization research based on double-flow flower topology model algorithm[J]. Computer Science, 2012, 39(9): 282－283. (in Chinese with English abstract)

[15] 樊亚春，谭小慧，周明全，等. 基于局部多尺度的三维模型草图检索方法[J]. 计算机学报，2017，40(11)：2448－2465.

Fan Yachun, Tan Xiaohui, Zhou Mingquan, et al. 3D model sketch retrieval method based on local multi-scale[J]. Chinese Journal of Computers, 2017, 40(11): 2448－2465. (in Chinese with English abstract)

[16] Gao F, Wu W, Lin Y, et al. Online safe trajectory generation for quadrotors using fast marching method and bernstein basis polynomial[C]//2018 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2018: 344－351.

[17] 淮永建，曾茜. 花卉植物形态与生长可视化仿真研究[J].计算机工程与应用，2012，48(8)：185－188.

Huai Yongjian, Zeng Qian. Visualization simulation of flower plant morphology and growth[J]. Computer Engineering and Applications, 2012, 48(8): 185－188. (in Chinese with English abstract)

[18] 白丽芳，常朝稳，王禹同，等. 基于有效约束的方向包围盒相交测试算法[J]. 计算机辅助设计与图形学学报，2016，28(10)：1757－1766.

Bai Lifang, Chang Chaowen, Wang Yutong, et al. Crossing test algorithm for direction bounding box based on effective constraints[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(10): 1757－1766. (in Chinese with English abstract)

[19] Isaac A S, Neumann C. Optimization of freeform surfaces using intelligent deformation techniques for LED applications[J]. Advanced Optical Technologies, 2018, 7(1/2): 67－80.

[20] Zhang D, Ren N, Hou X. An improved logistic regression model based on a spatially weighted technique (ILRBSWT v1. 0) and its application to mineral prospectivity mapping[J]. Geoscientific Model Development, 2018, 11(6): 2525－2539.

[21] 孙家泽，陈皓，耿国华. 三维文物点云模型配准优化算法[J]. 计算机辅助设计与图形学学报，2016，28(7)：1068－1074.

Sun Jiaze, Chen Hao, Geng Guohua. Registration optimization algorithm for 3D cultural object point cloud model [J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(7): 1068－1074. (in Chinese with English abstract)

[22] Rubio R R, Shehata J, Kournoutas I, et al. Construction of neuroanatomical volumetric models using 3-Dimensional scanning techniques: technical note and applications[J]. World Neurosurgery, 2019, 126: 359－368.

[23] Yin K, Huang H, Zhang H, et al. Morfit: Interactive surface reconstruction from incomplete point clouds with curve-driven topology and geometry control[J]. ACM Trans Graph, 2014, 33(6): 1－12.

[24] Islam M A, Murthy A, Bartocci E, et al. Model-order reduction of ion channel dynamics using approximate bisimulation[J]. Theoretical Computer Science, 2015, 599(27): 34－46.

[25] 胡良臣，寿华好. 求解带法向约束样条曲线逼近问题[J].计算机辅助设计与图形学学报，2016，28(9)：1443－1450.

Hu Liangchen, Shou Huahao. Solving the problem of approximating spline curves with normal constraints[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(9): 1443－1450. (in Chinese with English abstract)

[26] 张超，韩成，杨华民，等. 基于位姿约束的大视场双目视觉标定算法[J]. 光学学报，2016，36(1)：197－206.

Zhang Chao, Han Cheng, Yang Huamin, et al. Large-field binocular vision calibration algorithm based on pose constraint[J]. Acta Optica Sinica, 2016, 36(1): 197－206. (in Chinese with English abstract)

[27] 孙忱，奚宏生，高荣. 邻域线性最小二乘拟合的推荐支持度模型[J]. 西安交通大学学报，2015，49(6)：77－83.

Sun Chen, Xi Hongsheng, Gao Rong. Recommended support model for neighborhood linear least squares fitting[J]. Journal of Xi'an Jiaotong University, 2015, 49(6): 77－83. (in Chinese with English abstract)

[28] 王醒策，蔡建平，武仲科，等. 局部表面拟合的点云模型法向估计及重定向算法[J]. 计算机辅助设计与图形学学报，2015，27(4)：614－620.

Wang Xingce, Cai Jianping, Wu Zhongke, et al. Normal estimation and reorientation algorithm of point cloud model based on local surface fitting[J]. Journal of Computer-Aided Design & Computer Graphics, 2015, 27(4): 614－620. (in Chinese with English abstract)

[29] 焦迪，杨猛，杨刚. 基于物理的花开花落与叶片时变动态算法[J]. 系统仿真学报，2018，30(6)：85－94.

Jiao Di, Yang Meng, Yang Gang. Physic-based flowering and flowering time-varying dynamic algorithm [J]. Journal of System Simulation, 2018, 30(6): 85－94. (in Chinese with English abstract)

[30] Ouyang S G, Wang G, Yao J Y, et al. A Unity3D‐based interactive three‐dimensional virtual practice platform for chemical engineering[J]. Computer Applications in Engineering Education, 2018, 26(1): 91－100.

[31] Li J, Liu M, Xu W, et al. Boundary‐dominant flower blooming simulation[J]. Computer Animation and Virtual Worlds, 2015, 26(3/4): 433－443.

Simulation of plant petal shape change and growth based on 3D point cloud data

Huai Yongjian, Yang Danqi, Cai Dongna

(,100083,)

Different graphic techniques and methods are usually presented to simulate the 3D plant shape structure and growth in the field of virtual plant and visualization. Research results had been widely used in agriculture, forestry, landscape design, game, VR and computer animation, especially in plant shape structure-function modeling and natural landscape reconstruction. At present, the shape, color, texture and other morphological structure characteristics of the plants are mainly simulated by using the algorithms of computer graphics and rendering technology. The L-system is used to describe the geometry shape of plant and has faced the challenge of simulating the growth for complicated plant structure such as flower development. In this study, we present a method to describe the flower plant shape modeling and growth deformation based-on the scanning 3D point cloud data to avoid the complex plant procedural modeling. At first, we obtained the flower plant point cloud data in different growth development stages by using the 3D scanning device, and the sample data required for the function fitting and deforming by segmenting and intercepting the point cloud model. The sample data was fitted to summarize the growth rules of flower plant by using the tools of MATLAB and specified functional model. Then we combined the traditional flower growth simulation with the free-form deformation algorithm (FFD) based on the point cloud model. The traditional method deformed the shape by dragging the control point on the bounding box. But we made the control point move automatically, where the outside control points were driven to deform according to the growth function. In order to realize the operation of spatial points in the free-form deformation algorithm, the control points were converted from the world coordinates to local coordinates. Regardless of the world coordinates of the control points how to change, there were fixed local coordinates of the points take part in the mathematic transform. To fit the growth model of flowers, a special sampling and fitting method was designed. First, the flower was divided into different growth patterns and sampled separately according to the shape structure, we could get the fitting function by using the sample data. Then the real-time dynamic process of plant growth was operated by combining the growth function and deformation algorithm. To simulate the dynamic growth of flowers, a method was proposed based on the real measurement data of point cloud data model, which combined the FFD algorithm with the true growth principles to simulate the series change of petal shape. The test results showed that our method could maintain the plant morphological characteristics during the deformation and reconstruct the real process of plant growth according to the initial and final point cloud data, which could get a realistic visual effects. At last, we compared our deformation method with the physics-based simulation method and evaluate the algorithm precision by fitting regression analysis and measuring the geometry error between the real measure data and the reconstructed data. The results showed that the geometry deformation error could be controlled within 2 mm and the coefficient of determination was above 0.75 during the whole period of plant growth. The final reconstructed plant model was similar with the real plant and a novel approach was provided to simulate plant growth.

Three dimensional; deformation; models; virtual plant; point cloud; data fitting; plant deformation simulation

10.11975/j.issn.1002-6819.2019.15.020

TP391.9

A

1002-6819(2019)-15-0155-10

2019-01-20

2019-07-13

国家自然科学基金项目（31770589）；中央高校科研团队建设项目（2015ZCQ-XX）

淮永建，教授，博士生导师，博士，主要研究方向为虚拟现实、可视化。Email：huaiyj@163.com

淮永建，杨丹琦，蔡东娜. 基于三维点云数据的花瓣形态及生长过程模拟[J]. 农业工程学报，2019，35(15)：155－164. doi：10.11975/j.issn.1002-6819.2019.15.020 http://www.tcsae.org

Huai Yongjian, Yang Danqi, Cai Dongna. Simulation of plant petal shape change and growth based on 3D point cloud data[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(15): 155－164. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.15.020 http://www.tcsae.org