风送喷雾雾滴冠层穿透模型构建及应用

孙诚达，柳长鼎

风送喷雾雾滴冠层穿透模型构建及应用

孙诚达1，柳长鼎2

（1. 绍兴文理学院机械与电气工程学院，绍兴 312000；2. 南京农业大学工学院，南京 210031）

研究雾滴在树冠内的分布规律，对优化喷雾参数，提高喷雾效果有重要意义。该文以叶密度、出口风速和取样深度为试验变量，用试验法研究了树冠内雾滴穿透比例分布规律；试验结果表明：雾滴穿透比例随叶密度、取样深度的增加而减小，随喷雾机出口风速的增大而增大，其中取样深度对穿透比例影响最为显著。在此基础上，结合试验数据与统计学方法，构建了雾滴穿透比例二次指数数学模型，并确定了模型的待定系数，其模型精度2高于0.95，经检验模型有一定的合理性和可靠性。基于此模型，计算了雾滴冠后飘移率，与实测值相比，平均相对误差为16.73%。进一步对雾滴冠后飘移率影响因素、双面喷雾机理、喷雾参数优化进行了分析，拓展了模型应用，对模型局限性和进一步优化模型的后续研究设想展开了说明。研究对风送喷雾雾滴分布规律研究具有一定的参考价值。

喷雾；雾滴；模型；冠层穿透

0 引 言

雾滴在树冠内分布状况是衡量喷雾效果好坏的一个重要指标。研究雾滴在树冠内的分布规律，对优化喷雾参数，提高喷雾效果有十分重要意义[1-4]。当前对雾滴在树冠内的分布规律研究方法主要有：试验法、仿真分析法和理论建模法。

试验法是研究树冠内雾滴分布规律的常用方法。张晓辛等[5]研究了喷雾机导流板角度及喷头喷雾方向角度对雾滴在果树冠层内穿透沉积的影响；何雄奎等[6]通过改变果园风送式喷雾机风机风量，研究苹果树冠内风速的变化对靶标上农药沉积量的影响；吕晓兰等[7]以仿真树为试验对象，研究了喷雾压力、风机出口风速等因素对冠层内沉积覆盖率的影响；顾家冰[8]对风送五指喷雾机气雾流场开展了试验研究；Cross等[9-10]探究喷雾机风量、喷雾量等因素对不同大小苹果树冠内雾滴分布的影响；Farooq等[11]研究了不同喷雾量、风量条件下，不同大小树冠内雾滴分布状况。上述研究揭示了许多风送喷雾规律，但对树冠内雾滴分布预测、适合不同生长期作物喷雾参数的确定还有许多研究空间。

一些学者借助计算流体力学技术对雾流场开展研究[12-17]，为雾滴分布规律研究提供了许多可以借鉴的成果。如何更准确模拟作物实际状态，如茎叶、孔隙率等特征[18-22]，使仿真结果更接近实际情况，是当前喷雾仿真研究的重要内容。一些学者尝试使用纯理论建模方法对树冠内气雾流场分布规律进行探究，如Walklate等[23]结合理论推导和试验方法，对均质的理想仿真树内气流速度分布状况进行了分析，发现即使是理想树冠，其内部气流是非均匀的，而实际树冠特征则更加复杂，气雾流会以非均匀的状态穿过树冠，这给理论方法建模带来不少困难。

本文选取腊梅、早樱、花石榴和梨树4种不同树种为喷雾试验对象，研究在不同树冠密度、树冠尺寸和喷雾机出口风速条件下，雾滴在冠层内的分布规律；在此基础上，根据试验数据规律，结合统计学拟合方法，构建风送喷雾雾滴穿透比例模型；使用模型对雾滴在树冠内的分布进行预测、为优化风速从而较好地控制雾滴的冠后飘移、提高药液利用率、优化喷雾参数提供决策依据，对双侧喷雾必要性进行了应用性说明。

1 雾滴穿透比例界定

为便于对雾滴在树冠内的穿透性能进行量化分析，本文把喷雾方向上，进入树冠内单位竖直面上平均雾量与刚进入树冠前边缘单位竖直面上平均雾量的比值定义为“雾滴穿透比例”。可用公式表示为

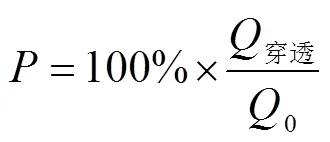
式中为雾滴穿透比例，%；穿透为树冠内单位竖直面上平均雾量，mg/cm2；0为刚进入树冠前边缘单位竖直面上平均雾量，mg/cm2。

2 材料及方法

2.1 喷雾机

试验用圆盘式风送喷雾机和多风管风送喷雾机为喷雾试验平台。喷雾时间通过时间继电器可精确设置，喷雾压力通过调压阀控制。部分喷雾参数设置如下：喷雾压强1.5 MPa，圆盘式风送喷雾机喷雾方向呈水平，喷头离树冠距离为50 cm，喷雾时间3 s；多风管风送喷雾机行驶速度为1.0 m/s，喷头离树冠距离为50 cm，风机转速通过变频器调节，由于出口风速作为研究变量更具有一般意义，因此试验前对不同风机转速下的出口风速作了预先的标定，标定时在出风口选择了中心、周边5个测量点，然后求出口风速均值。标定后可通过对风机转速的调节实现对出口风速的调节，试验选用的出口风速值如表1所示。

2.2 喷雾试验

为了研究不同种类、不同疏密程度和不同大小树冠对雾滴分布规律影响，用圆盘式风送喷雾机对腊梅、早樱、花石榴、梨树大小接近的不同生长期的4种树冠进行喷雾试验；用多风管风送喷雾机对大、中、小梨树进行喷雾试验。树冠疏密程度以叶面积体密度[24]（以下简称叶密度）量化描述，其测量方法如下：使用40 cm× 40 cm×40 cm的样框，插入树冠的多个不同区域（本试验选5个），统计并记录各个框选区域内的叶片数目；在各个框选区域中，用相机随机拍摄大小不一、一定数量树叶，使用图像处理方法[25]可得各样本叶片面积，如图1所示；用样本树叶面积平均值，作为对应样框内的叶面积总体均值。最终，以各样框的叶面积体密度平均值作为该树冠的叶面积体密度。所得结果如表2所示。

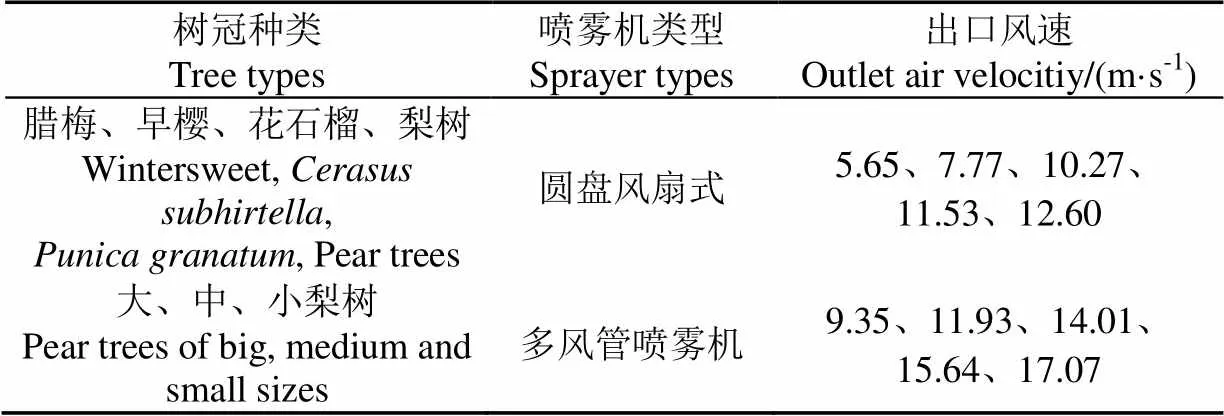
表1 喷雾机出口风速值

图1 叶密度测量示意图

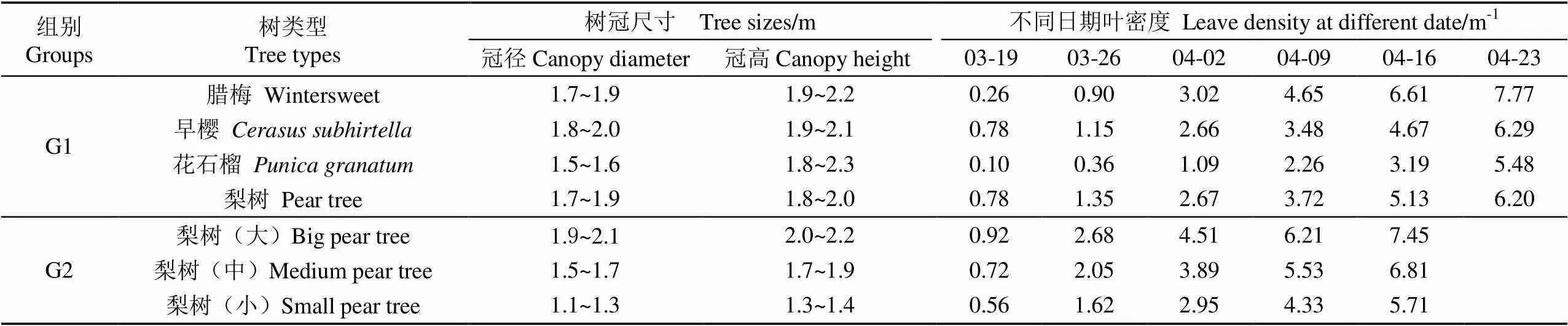
表2 4种类型树冠叶密度测量结果

由于雾量采集数据比较多，本文采用基于溶液电导率的雾量实时测量系统[26]来测量雾量，测量系统硬件部分由雾滴采样盒、DDG-3023电导率测量仪、420MA-IN32电流模拟量采集模块及PC机的硬件平台等组成；软件部分利用Matlab中有关函数将从串口读进来的数据按列顺序存放在矩阵中，利用画图函数对数据规律用图线显示，同时以表格形式显示测量数据；系统用xlswrite函数把测量数据存入Excel的对应表中，供后继进一步分析、调用。该测量系统能连续、实时测量多个方向雾量，并能与PC机通讯，实现数据实时处理、显示和存取。

树冠内雾量采集样点设置如下：沿喷雾方向将树冠从前向后分成若干层，采样点设置、各层间距和测量点间距视树冠大小而定，每层上下左右布置A、B、C…、M9～13个测量点，测量点A、E、I间距为30～50 cm，A、B、C间距为30～60 cm，各层F、F+1间距为24～46 cm，如图2所示。

雾滴穿透比例测量方法如下：1）沿喷雾方向将树冠从前向后等分成若干层，每层在实地定位支架的上中下3根横梁滑杆上共布置A、B、C、…、M9～13个测量点，如图2所示，雾滴采样盒固定在各测量点上，采集面与喷雾方向垂直；2）为避免前面采样盒对后面采样的遮挡，3根横梁滑杆可在定位支架水平导轨上前后平移至各等分层上，移动时遇到树枝，可先将横梁滑杆抽出树冠，再从树冠外侧将横梁滑杆插入树冠内下一测量层位置；3）某一出口风速下，逐一完成各层采样点雾量测量；4）改变风机转速，重复步骤3），直至完成表1中5个出口风速下，各层采样点雾量测量；5）根据各采样点雾量测量值和雾滴采集面积，计算采样处单位雾滴采集面上平均雾量；6）为了便于定量分析，用同一层上各采样处单位雾滴采集面上平均雾量代表该层树冠竖直截面上平均雾量，利用式（2）计算该层上雾滴平均穿透比例（以下简称“雾滴穿透比例”）。

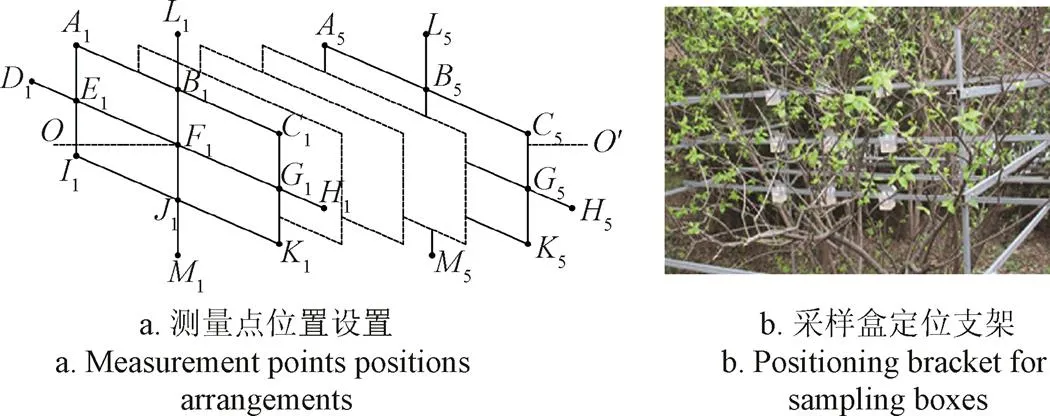
图2 测量点及采样盒设置

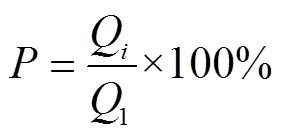
式中1树冠前边缘第一层采样处单位面积上平均雾量，mg/cm2；Q为第层采样处单位面积上平均雾量，mg/cm2。

3 雾滴冠层穿透模型构建及验证

3.1 模型构建

根据测量值，可初步分析雾滴穿透比例随取样深度、出口风速和叶密度变化规律。限于篇幅，随机列举了部分雾滴穿透比例随取样深度、出口风速和叶密度变化规律曲线，见图3。树冠中雾滴穿透比例随叶密度、取样深度的增加而减小，且取样深度对雾滴影响比叶密度要明显；雾滴穿透比例随出口风速的增大而增大，当风速增大到一定值时，雾滴穿透比例增加趋缓。分析其他参数下获得的多组试验数据，也可得出类似变化规律。

以出口风速、叶密度、取样深度、其他综合影响变量为自变量，雾滴穿透比例为因变量，构建模型。根据图3中曲线形式，假定5种模型表达式，基于不同生长期树冠试验测量数据和SPSS 20.0拟合建模，以决定系数（2）、均方根误差（root mean square error，RMSE）[27]进行模型评价。

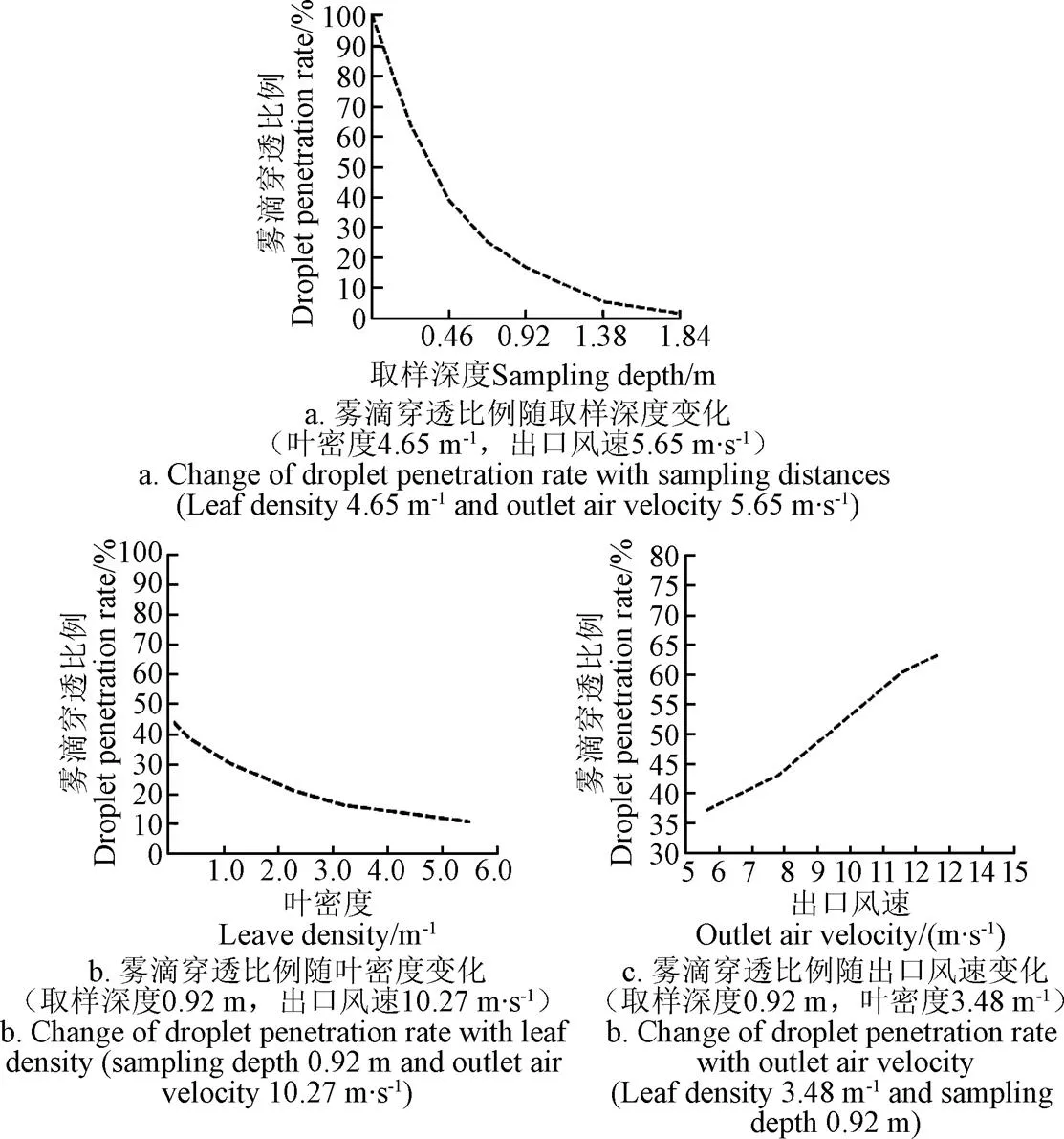
注：图a为腊梅树，图b为花石榴树，图c为早樱树。

如表3所示，二次指数衰减模型对穿透比例因变量与，，自变量拟合的2最大（均高于0.95），RMSE最小（4.1%~5.0%），因此，假定式（3）为雾滴穿透比例衰减模型的数学表达式。

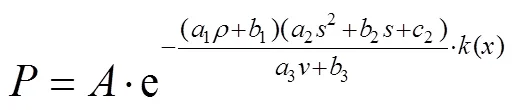
式中()为其他影响因素（如喷雾压力、喷雾流量等）对雾滴穿透比例的综合影响，其余变量见表3。

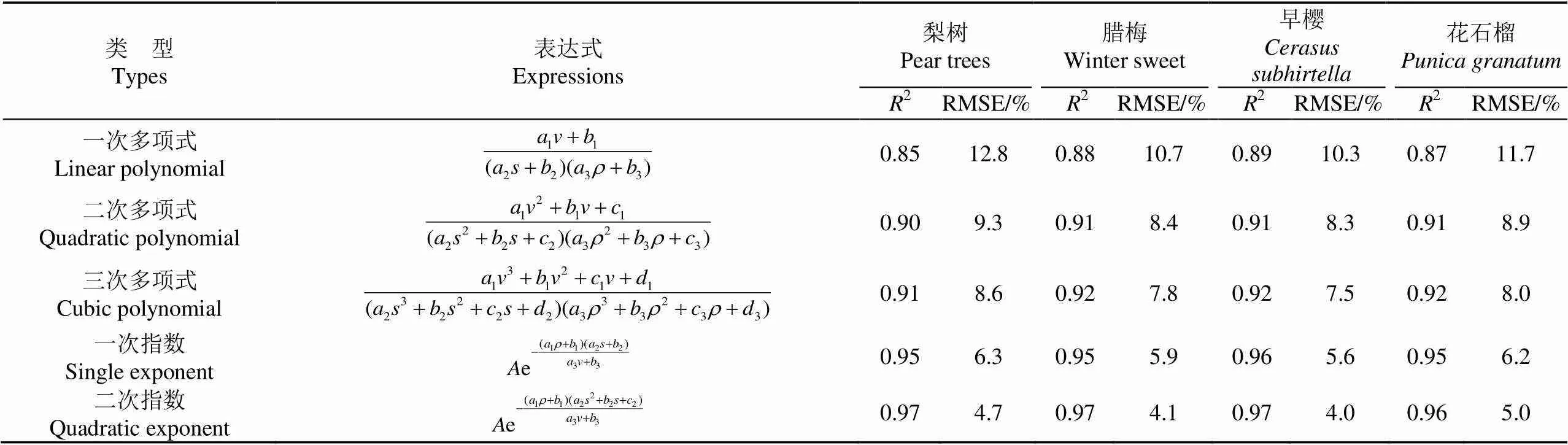
表3 5种模型拟合结果比较

注：2是决定系数；RMSE是均方根误差；表示出口风速，m·s-1；表示叶密度，m-1；表示取样深度，m；其他为模型系数。

Note:2is determination coefficient; RMSE is root mean square error;is outlet air velocity, m·s-1;is leave density, m-1;is sampling depth, m; othersare model coefficients.

本文研究叶密度、出口风速和取样深度3个变量对雾滴穿透比例的影响规律，暂不考虑其他影响因素，()为常数。由此，式（3）中有8个系数有待确定。表4为圆盘风送喷雾机及多风管果园风送喷雾机在不同树冠中雾滴穿透模型的系数值。对每种树冠确定1套系数值，试验工作量较大，故本对枝叶结构相近的不同大小、不同类型树冠混合建模，G1和G2混合组建模的2分别为0.96和0.95，RMSE分别为5.3%和5.7%。

表4 梨树、腊梅、早樱、花石榴树冠中雾滴冠层穿透二次指数模型的系数值

3.2 雾滴冠层穿透模型验证

3.2.1 相同喷雾机械在相同树冠中的验证分析

圆盘型喷雾机对腊梅（叶密度为6.61 m-1）进行喷雾试验，用于雾滴穿透比例模型验证，结果如表5，测量值与模型预测值的平均相对误差为13%～18%，表明建立的雾滴穿透模型可靠。

表5 腊梅叶雾滴冠层穿透比例预测精度

3.2.2 相同喷雾机械在不同大小树冠中的验证分析

在出口风速14.01 m/s，小、中、大梨树叶密度分别为5.08、6.12、7.25 m-1时，采用多风管风送喷雾机对小、中、大梨树喷雾，用于模型验证，结果如表6。雾滴穿透比例模型验证试验的测量值与模型预测值平均相对误差为5%～28%。可见，相同喷雾机械在不同大小同种树冠喷雾时，所建立的雾滴穿透比例模型，有相近的预测精度，且预测精度较高。

3.2.3 同种喷雾机在不同种树冠中的验证分析

出口风速为10.27 m/s，采用圆盘型喷雾机对叶密度分别为6.02、1.15、3.19 m-1的腊梅、早樱、花石榴树冠进行喷雾，用于模型验证，结果如表7，测量值与预测值相对误差为7%～22%。可见，相同喷雾机械在不同种树冠喷雾时，所建立的雾滴穿透比例模型，有相近的预测精度。

综上，不同树冠、不同喷雾机械，只要在试验数据的基础上，单独确立一定模型系数，模型有较高的预测精度，说明模型式（3）假设有一定的合理性、可靠性。

表6 多风管喷雾机对梨树喷雾时雾滴穿透比例预测精度

表7 圆盘风送喷雾机对3种树喷雾时雾滴穿透比例预测精度

3.2.4 混合模型验证

表8对比了腊梅、梨树、早樱、花石榴4种树冠单一模型和混合模型预测精度。由表可知，G3和G5组用混合模型预测误差比单独模型的预测误差略大，G5组使用单独模型预测相对误差约18%，使用混合模型预测相对误差约21%，混合模型误差稍大，但影响不大。然而，在花石榴中，用混合模型预测误差较大，原因是花石榴的枝叶结构与其他果树差异比较大。

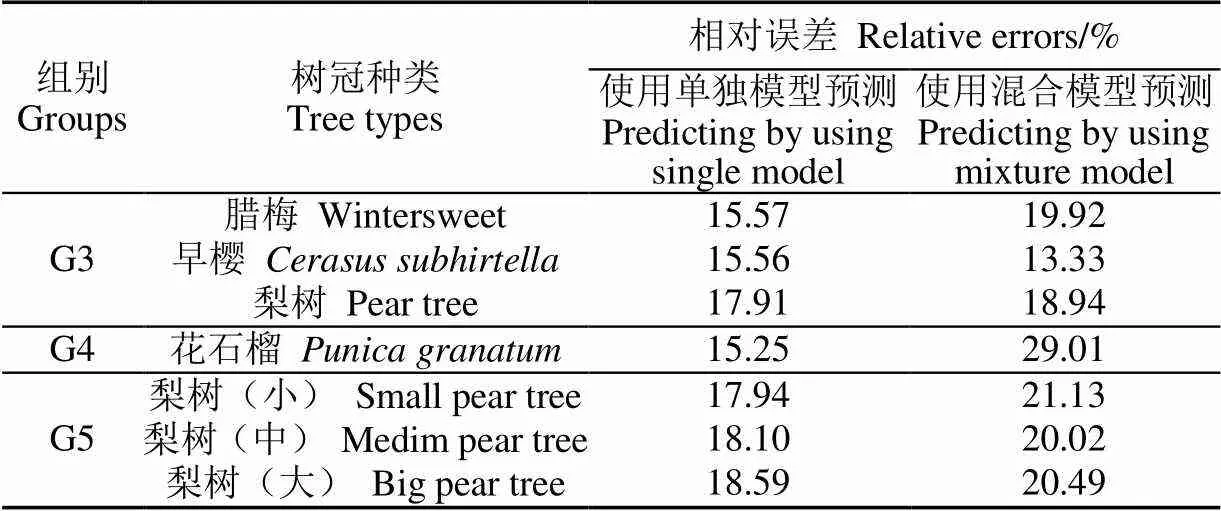
表8 4种树冠单一模型和混合模型预测误差比较

4 模型应用

4.1 使用模型进行雾滴飘移率影响因素的分析

减少雾滴损失是风送喷雾的重要目标[28-30]。雾滴损失主要体现在3个方面：地面沉积、空中逃逸、冠后飘移。雾滴冠后飘移量是指沿喷雾方向透过树冠到了外面的雾滴。用雾滴冠后飘移率定量分析研究雾滴冠后飘移程度，其计算公式为

=out/in×100% （4）

式中为飘移率，%；out为雾滴流出树冠总量，mg；in为流入树冠雾滴总量，mg。为便于计算，用第1层和最后1层平均雾滴穿透量来表示雾滴流入树冠总量和流出树冠总量。

从雾滴冠层穿透比例模型角度讲，雾滴飘移率可认为是树冠中最后1层的雾滴穿透比例。以早樱树冠为例，结合试验数据，检验模型对雾滴冠后飘移率预测的准确性，图4为出口风速5.65、7.77、10.27、11.53、12.60 m/s下，叶密度为1.15 m-1早樱树冠雾滴冠后飘移率实际测量值和模型曲线计算值的对比分析，平均相对误差为16.73%。可见，使用模型对雾滴冠后飘移率预测分析有较高准确性。

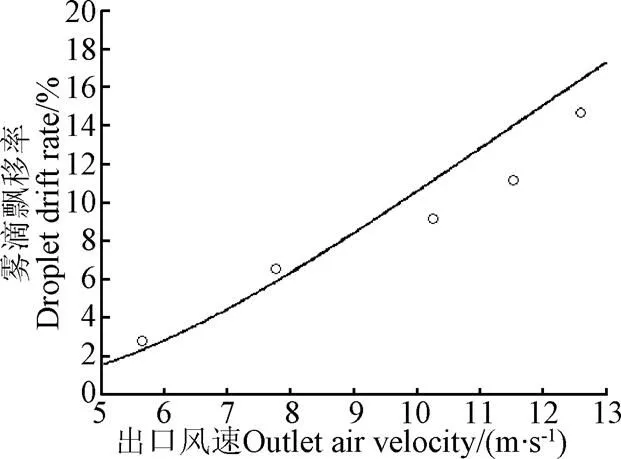
注：图中○为实际测量值，实线为模型表达式曲线，叶密度为1.15 m-1。

以早樱树冠为例，用模型对在雾滴冠后飘移影响因素作进一步说明。分析图5可知，当出口风速一定时，雾滴飘移率随着叶密度增加而减少。如出口风速为9 m/s时，叶密度0.78m-1增至6.29m-1，所对应的冠后飘移率由10%下降至1%。当叶密度一定时，雾滴飘移率随出口风速增加而增大。如叶密度为0.78 m-1时，出口风速由5 m/s增至12 m/s的过程中，雾滴穿透比例由2%增至17%。

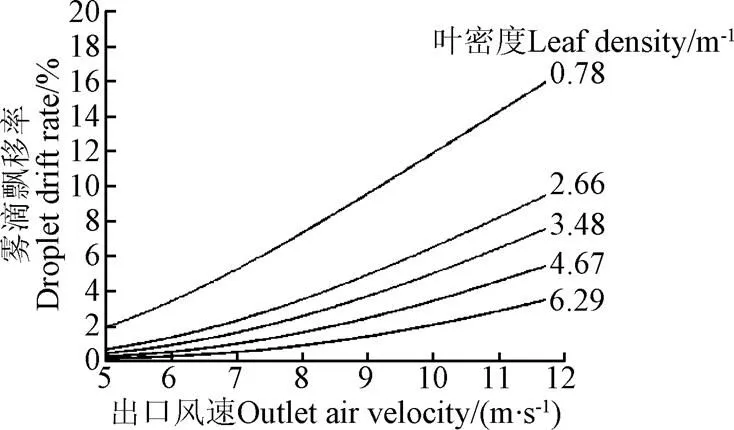
图5 早樱中雾滴飘移率与出口风速、叶密度的关系

综上，雾滴飘移率与出口风速、叶密度有关。为减小雾滴飘移，对不同叶密度树冠，应控制不同的出口风速。但出口风速过小，会影响雾滴到达树冠的各个区域，因此，要两方面兼顾，才能确定最佳出口风速。这为优化喷雾参数提供依据。

4.2 使用模型分析雾滴在树冠内各个区域的分布状况

用模型对雾滴在树冠各个区域内滞留比例作定量分析。单侧喷雾时，某区域可看作由树冠外表面，与喷雾方向垂直的前端竖直平面和后端竖直平面所围成的空间。设前端竖直面与后端竖直面离树冠最前端的距离分别为1和2，利用式（5）得到该区域雾滴滞留比例计算公式为

式中滞留为树冠内该区域的雾滴滞留比例，%；其他变量为模型系数。同理可计算另一侧喷雾时，对应区域的雾滴滞留比例。

图6为双侧喷雾示意图，树冠被分成1，2，…，Z若干区域。

图6 双侧喷雾树冠内采样层分布示意图

双侧喷雾时雾滴在树冠区域Z中的滞留率可按式（6）计算

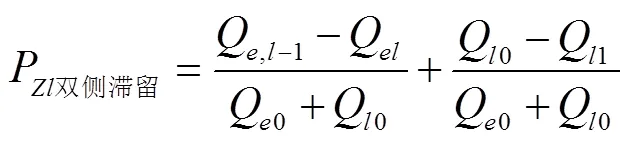
式中Q0、Q,l-1和Q分别为一侧喷雾时树冠0层、e-1层、e层处单位面积上的平均雾量，mg/cm2；Q0和Q1为另一侧喷雾时分别与e层和e1层对应的树冠0层和1层单位面积上的平均雾量，mg/cm2；P双侧滞留为双侧喷雾方式下，区域Z中的雾滴滞留率，%。

为便于计算，近似认为两侧喷雾参数相同，一侧喷雾与另一侧喷雾时进入树冠雾量相等，即Q0=Q0。于是，式（6）可简化为

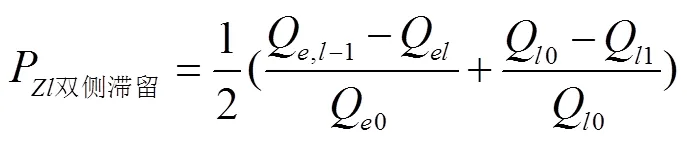
也即双侧喷雾时雾滴的滞留比例等于各自对应区域单侧喷雾时雾滴滞留比例和的50%。

雾滴滞留比例除了可以表示成式（5）外，还可表示为

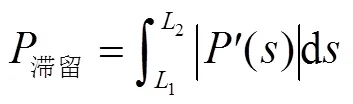
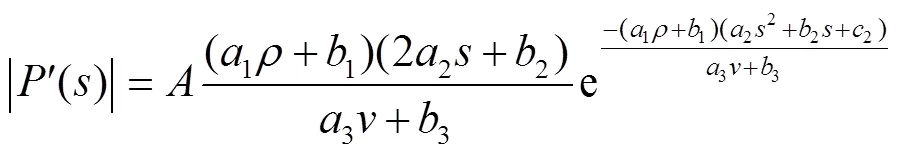
式中()为雾滴穿透比例对取样深度一次求导，即穿透比例随距离变化率；1、2为前后竖直面所在位置对应的取样深度，m。、1、1、2、2、2、3、3为模型系数值。

以腊梅树冠为例，雾滴穿透比例变化率对取样深度的变化曲线（叶密度为6.02 m-1，出口风速为12.60m/s）如图7所示。

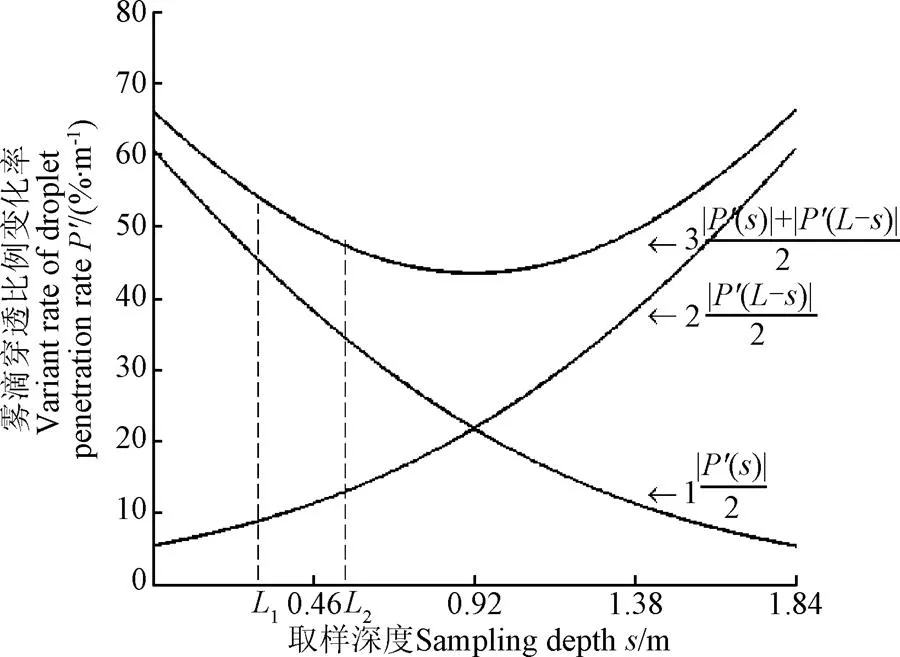
注：叶密度为6.02 m-1，风速为12.60 m·s-1，L为树冠冠幅。曲线1是单侧喷雾，双侧喷雾时进入树冠雾量可近似认为是单侧喷雾时的2倍；曲线2是另一侧喷雾时，曲线3为两侧喷雾时。

由1、2、轴分别与曲线1、2、3围成面积分别代表一侧喷雾，另一侧喷雾，双侧喷雾方式下树冠内所选区域的雾滴滞留比例。对图7曲线1分析可知，单位取样深度内雾滴滞留比例随取样深度增加明显减小，树冠雾滴分布均匀性较差。分析曲线3可知，单位取样深度内雾滴滞留比例随取样深度增加先略微下降后又逐渐增加，表明双侧树冠内雾滴分布的均匀性较好。对不同种类，不同叶密度树冠，在不同的出口风速下喷雾，通过比较曲线的平缓程度可说明雾滴在树冠内的分布均匀性好坏，从而可确定合适的喷雾参数值。

除了定性观察曲线的平缓程度来分析雾滴在树冠内分布均匀性，也可以通过定量计算来进一步分析：将整个树冠沿着喷雾方向分成若干个区间，由式（5）可求得单侧喷雾时树冠各个区域内雾滴的滞留比例（也可通过对式（8）积分计算获得），进而可求得双侧喷雾方式下选定各区域的雾滴滞留比例。通过计算各个区域内雾滴滞留比例的变异系数来评价雾滴在树冠内的分布均匀性。对应的变异系数越小，表明树冠内雾滴分布越均匀。

滞留比例变异系数测量方法如下：将整个树冠分成若干区域（视树冠大小而定），先分别测量两侧单独喷雾时对应的雾滴穿透比例，可计算单侧喷雾时各个区域内滞留比例，双侧喷雾雾滴滞留比例为选定区域内，各自单侧喷雾时滞留比例之和的50%，最后计算各个区域内雾滴滞留比例的变异系数。表9所示为双侧喷雾方式下腊梅树冠中（叶密度为6.02 m-1）雾滴滞留比例变异系数测量值和模型预测值，相对误差为17%～25%，可见利用模型对双侧喷雾中雾滴分布状况定量分析有一定的可行性。

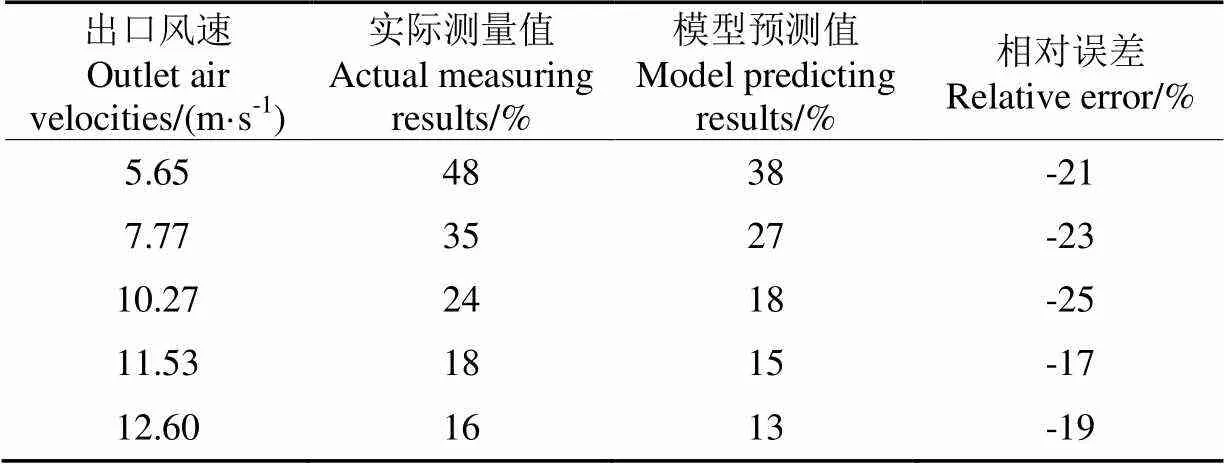
表9 双侧喷雾模式下叶密度为6.02 m-1腊梅树冠中雾滴滞留比例变异系数

5 结 论

本文以叶密度、出口风速和取样深度为试验变量，用试验法研究了树冠内雾滴穿透比例分布规律。结果表明，叶密度、出口风速和取样深度对雾滴穿透比例有影响，其中取样深度影响最为显著。在此基础上，基于大量数据和统计学方法，构建了雾滴穿透比例二次指数数学模型，其模型精度2高于0.95。最后通过模型对雾滴飘移率影响因素，双面喷雾机理、喷雾参数优化等实用性分析，说明模型有一定的实用性。本文对风送喷雾雾滴分布规律研究有一定参考价值。

本文通过构建雾滴穿透比例模型来研究风送喷雾雾滴分布规律，但许多方面有待后续研究中逐步完善。

1）对影响模型的其他因素没有足够考虑，如：喷雾压强、管路流量、环境温度、湿度等，这些试验因素对雾滴穿透比例的影响有待进一步的研究。

2）受测量条件制约，试验中在某一取样深度下，只选取了若干有代表性的采样点，并用采样处雾量的平均值来作为这一层雾量的平均值，会对模型精度造成一定影响，如何提高测量效率，增加采样点，进一步提高模型精确性，有待进一步研究。

3）本文虽对枝叶结构相类似树冠进行了混合建模的尝试，但试验所选树冠种类仍显不足，影响模型适用范围，有待进一步研究。

[1] 何雄奎. 改变我国植保机械和施药技术严重落后的现状[J]. 农业工程学报，2004，20(1)：13－15.

He Xiongkui. Improving severe draggling actuality of plant protection machinery and its application techniques[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2004, 20(1): 13－15.(in Chinese with English abstract)

[2] 翟长远，赵春江，Ning Wang，等. 果园风送喷雾精准控制方法研究进展[J]. 农业工程学报，2018，34(10)：1－15.

Zhai Changyuan, Zhao Chunjiang, Ning Wang, et al. Research progress on precision control methods of air-assisted spraying in orchards[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(10): 1－15.(in Chinese with English abstract)

[3] 周良富，薛新宇，周立新，等. 果园变量喷雾技术研究现状与前景分析[J]. 农业工程学报，2017，33(23)：80－92.

Zhou Liangfu, Xue Xinyu, Zhou Lixin, et al. Research situation and progress analysis on orchard variable rate spraying technology[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(23): 80－92. (in Chinese with English abstract)

[4] 孙诚达，邱威，丁为民，等. 梨树风送喷雾关键作业参数优化与试验[J]. 农业工程学报，2015，31(24)：30－38.

Sun Chengda, Qiu Wei, Ding Weimin, et al. Parameter optimization and experiment of air-assisted spraying on pear trees[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(24): 30－38. (in Chinese with English abstract)

[5] 张晓辛，吕晓兰，丁素明，等. 果园风送式喷雾机仿形喷雾试验研究[J]. 中国农机化，2011(3)：68－72.

Zhang Xiaoxin, Lü Xiaolan, Ding Suming, et al. Experimental research on profiling spray of air-assisted orchard sprayer[J]. Chinese Agricultural Mechanization, 2011(3):68－72.(in Chinese with English abstract)

[6] 何雄奎，曾爱军，何娟. 果园喷雾机风速对雾滴的沉积分布影响研究[J]. 农业工程学报，2002，18(4)：75－77.

He Xiongkui, Zeng Aijun, He Juan. Effect of wind velocity from orchard sprayer on droplet deposit and distribution[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2002, 18(4): 75－77. (in Chinese with English abstract)

[7] 吕晓兰，傅锡敏，吴萍，等. 喷雾技术参数对雾滴沉积分布影响试验[J]. 农业机械学报，2011，42(6)：70－75.

Lü Xiaolan, Fu Ximin, Wu Ping, et al. Influence of spray operating parameters on droplet deposition[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(6): 70－75. (in Chinese with English abstract)

[8] 顾家冰. 风送式变量喷雾机气液两相流及雾化的试验研究[D].南京：南京农业大学，2012.

Gu Jiabing. Atomization and Air-droplet Flow Fields of an Air-assisted Variable-rate Sprayer for Tree Crop Application[D]. Nanjing: Nanjing Agricultural University, 2012. (in Chinese with English abstract)

[9] Cross J V, Walklate P J, Murray R A, et al. Spray deposits and losses in different sized apple trees from an axial fan orchard sprayer: 1.Effects of spray liquid flow rate[J]. Crop Protection, 2001, 20(1): 13－30.

[10] Cross J V, Walklate P J, Murray R A, et al. Spray deposits and losses in different sized apple trees from an axial fan orchard sprayer: 3. Effects of air volumetric flow rate[J]. Crop Protection, 2003, 22(2): 381－394.

[11] Farooq M, Salyani M.Spray penetration into the citrus tree canopy from two air-carrier sprayers[J]. Transactions of the ASAE, 2002, 45: 1287－1293.

[12] 杨风波，薛新宇，蔡晨，等. 多旋翼植保无人机悬停下洗气流对雾滴运动规律的影响[J]. 农业工程学报，2018，34(2)：64－73.

Yang Fengbo, Xue Xinyu, Cai Chen, et al. Effect of down wash airflow in hover on droplet motion law for multi-rotor unmanned plant protection machine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(2): 64－73. (in Chinese with English abstract)

[13] 丁天航，曹曙明，薛新宇，等.果园喷雾机单双风机风道气流场仿真与试验[J]. 农业工程学报，2016，32(14)：62－68.

Ding Tianhang, Cao Shuming, Xue Xinyu, et al. Simulation and experiment on single-channel and double-channel airflow field of orchard sprayer[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(14): 62－68. (in Chinese with English abstract)

[14] 祁力钧，赵亚青，王俊，等. 基于CFD的果园风送式喷雾机雾滴分布特性研究[J]. 农业机械学报，2010，41(2)：62－67.

Qi Lijun, Zhao Yaqing, Wang Jun, et al. CFD simulation and experimental verification of droplet dispersion of air-assisted orchard sprayer[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(2): 62－67. (in Chinese with English abstract)

[15] Endalew M, Debaerb C, Ruttern N, et al. A new integrated CFD modeling approach towards air-assisted orchard spraying-PartⅠ: Model development and effect of wind speed and direction on sprayer airflow[J]. Computers and Electronics in Agricultural, 2010, 71(1): 128－136.

[16] Endalew M, Debaerb C, Ruttern N, et al. A new integrated CFD modeling approach towards air-assisted orchard spraying-PartⅡ: Validation for different sprayer types[J]. Computers and Electronics in Agricultural, 2010, 71(1): 137－147.

[17] Salcedo R, Granell R, Palau G, et al. Design and validation of a 2D CFD model of the airflow produced by an airblast sprayer during pesticide treatments of citrus[J]. Crop Protection, 2015, 116: 150－161.

[18] 吴升，赵春江，郭新宇，等. 基于点云的果树冠层叶片重建方法[J]. 农业工程学报，2017，33(增刊1)：212－218.

Wu Sheng, Zhao Chunjiang, Guo Xinyu, et al. Method of fruit tree canopy leaf reconstruction based on point cloud[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(Supp.1): 212－218. (in Chinese with English abstract)

[19] 方慧，杜朋朋，胡令潮，等. 基于可视化类库的植株三维形态配准方法及点云可视化[J]. 农业工程学报，2013，29(22)：180－188.

Fang Hui, Du Pengpeng, Hu Lingchao, et al. VTK-based plant 3D morphological visualization and registration[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(22): 180－188. (in Chinese with English abstract)

[20] 陆声链，郭新宇，李长锋. 三维植物叶片精确建模和绘制技术研究[J]. 中国图象图形学报，2009，14(4)：731－737.

Lu Shenglian, Guo Xinyu, Li Changfeng. Research on techniques for accurate modeling and rendering 3D plant leaf[J]. Journal of Image and Graphics, 2009, 14(4): 731－737. (in Chinese with English abstract)

[21] 张海淑. 静态孔隙率相似的空间雾滴沉积分布仿真与试验研究[D]. 泰安：山东农业大学，2018.

Zhang Haishu. Simulation and Experimental Study of Spatial Droplet Deposition Distribution With Similar Static Porosity[D]. Taian: Shandong Agricultural University, 2017. (in Chinese with English abstract)

[22] 陈荣康. 辅助气流作用下高郁闭度作物冠层孔隙率变化研究[D]. 泰安：山东农业大学，2017.

Chen Rongkang. Study on Canopy Porosity Change of High Canopy Density Under Auxiliary Air Flow[D]. Taian: Shan Dong Agricultural University, 2017.(in Chinese with English abstract)

[23] Walklate P J, Weiner K L, Parkin C S. Analysis of and experimental measurements made on a moving air-assisted sprayer with two-dimensional air-jets penetrating a uniform crop canopy[J]. Journal of Agricultural Engineering Research, 1996, 63: 365－378.

[24] 全国科学技术名词审定委员会. 生态学名词[M]. 北京：科学出版社，2006.

[25] 张强，王正林. 精通MATLAB图像处理[M]. 北京：电子工业出版社，2012.

[26] Sun Chengda, Qiu Wei, Ding Weimin, et al. Design and experiment of a real-time droplet accumulating mass measurement system[J]. Transactions of the ASABE, 2017, 60(3): 615－624.

[27] 武松，潘发明. SPSS统计分析大全[M]. 北京：清华大学出版社，2014.

[28] Hilz E, Vermeer A W P. Spray drift review: The extent to which a formulation can contribute to spray drift reduction[J]. Crop Protection, 2013, 44(1): 75－83.

[29] 傅泽田，祁力钧. 国内外农药使用状况及解决农药超量使用问题的途径[J]. 农业工程学报，1998，14(2)：7－12.

Fu Zetian, Qi Lijun. Over-use of pesticide and approaches to reduce pesticide dosage[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 1998, 14(2): 7－12. (in Chinese with English abstract)

[30] 刘秀娟，周宏平，郑加强. 农药雾滴飘移控制技术研究进展[J]. 农业工程学报，2005，21(1)：186－190.

Liu Xiujuan, Zhou Hongping, Zheng Jiaqiang. Research advances of technologies for spray drift control of pesticide application[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2005, 21(1): 186－190. (in Chinese with English abstract)

Construction and application of droplet canopy penetration model for air-assisted spraying pattern

Sun Chengda1, Liu Changding2

(1.,,312000,; 2.,,210031,)

Understanding droplet distribution inside tree canopy has a great significance on optimizing spray parameters and improving spray effect. In this article, distribution of droplet penetration rate inside tree canopy during air-assisted spraying was studied by experimental method. The droplet penetration rate was defined as the ratio of droplets inside canopy along unit vertical face to that before penetrating into the canopy. The change of droplet penetration rate with tree leaf density, outlet air velocity of sprayers and sampling depth was analyzed. Disc sprayer and multi air pipe sprayer were used to spray 4 types of tree canopies of pear trees (big, medium and small sizes), wintersweet, cerasus subhirtella and punica granatum. Droplet deposition was determined in real time. The results showed that the droplet penetration rate decreased as the leaf density and sampling depth increased while it increased with increased outlet air velocity of sprayer. Among the 3 test variables of tree leaf density, outlet air velocity of sprayer and sampling depth, the sampling depth greatly affected the droplet penetration rate. Following the changing pattern of droplet penetration rate with tree leaf density, outlet air velocity of sprayer and sampling depth, 5 types of models (linear polynomial, quadratic polynomial, cubic polynomial, single exponent and quadratic exponent) were assumed to fit the changing pattern of droplet penetration rate. The quadratic exponent model had the highest accuracy with2higher than 0.95 and the RMSE was the least from 4.1% to 5.0%. By experimental validation, the model still had relatively reliable accuracy. Thus, the quadratic exponential model was finally chosen as the suitable model. By using this model, it had to be built based on canopy of each tree. By mixing the data from different tree canopies, we tested the feasibility to estimate droplet penetration rate by a quadratic exponential model. The results showed that the2was still higher than 0.95 and root mean square error was 5.3%-5.7%. By validation, the relative error could be lower than 20% for mixture of wintersweet, cerasus subhirtella and pear trees but reach up to about 29% for punica granatum tree. It was because the branch structure of punica granatum was different from the other trees. The quadratic exponential model was then extended to application in calculating droplet drift rate after tree canopy in order to analyze its influencing factor. The droplet drift rate after Cerasus subhirtella tree canopy of different leaf density under different sprayer outlet air velocities was calculated using model and validated by test. The mean relative error was 16.73%, indicating that the model could be used to determine the suitable outlet air velocities for tree canopies of different growing stages and reduce the droplet drift rate. The variation coefficients of droplet distribution inside tree canopy were also calculated by the model, which was used to better explain the principle of double-side spraying pattern. In the end, the model limitation and subsequent research assumption to improve model were illustrated: spray pressure, flow rate, environmental temperature and humidity were approximately regarded as constants in this article, and in further researches, the influence on droplet penetration rate of these factors should be investigated. A unit model for estimating droplet penetration rate could be established if the tree types had similar branches and leaf structures, and in further researches, more types of trees should be chosen and classified to build mixture model to improve the model accuracy. This paper is helpful to understanding droplet distribution in tree canopy during air-assisted spraying.

spraying; droplets; models; canopy penetration

10.11975/j.issn.1002-6819.2019.15.004

S491+.1

A

1002-6819(2019)-15-0025-08

2018-12-13

2019-07-10

浙江省基础公益研究计划项目“雾量在线测量系统的设计及其关键技术研究”（LGN19C140004）

孙诚达，博士，讲师，主要从事智能精准施药技术与装备研究。Email：njauscd@163.com

孙诚达，柳长鼎. 风送喷雾雾滴冠层穿透模型构建及应用[J]. 农业工程学报，2019，35(15)：25－32. doi：10.11975/j.issn.1002-6819.2019.15.004 http://www.tcsae.org

Sun Chengda, Liu Changding. Construction and application of droplet canopy penetration model for air-assisted spraying pattern[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(15): 25－32. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.15.004 http://www.tcsae.org