基于弹性地基梁理论的梯形渠道混凝土衬砌冻胀力学模型

李宗利，姚希望，杨 乐，邵化建，王正中

基于弹性地基梁理论的梯形渠道混凝土衬砌冻胀力学模型

李宗利1,2，姚希望1，杨 乐1，邵化建1，王正中1,2

（1. 西北农林科技大学水利与建筑工程学院，杨凌 712100；2. 西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌 712100）

冻胀破坏是寒区渠道衬砌破坏的主要方式，建立合理的冻胀力学模型是渠道衬砌抗冻胀设计的基础。该文基于Winkler假定，将渠道基土的冻胀效应等效为一组相互独立且垂直或平行于衬砌板的弹簧。冻胀量通过弹簧的伸长量体现，冻胀力通过弹簧被压缩产生的反力体现。结合梯形渠道冻胀时衬砌板的受力特点，应用SL23-2006《渠系工程抗冻胀设计规范》冻胀量的计算成果，建立基于弹性地基梁理论的梯形渠道混凝土衬砌冻胀力学模型，其合理性通过与甘肃省靖会总干渠梯形渠道的前人试验和数值模拟结果进行比较验证。结果表明，该文模型计算的冻胀量和冻胀反力的分布规律与前人的试验和数值模拟基本吻合；计算的冻胀量和试验结果整体相对平均误差为4.72%，计算结果合理。该文模型与现行规范推荐的冻胀量计算成果有机衔接，可为寒区渠道抗冻胀设计提供参考。

渠道；冻土；位移；弹性地基梁；力学模型

0 引 言

中国受到季节性冻土和多年冻土影响的区域面积占中国陆地总面积的70%左右[1]。在这些地区，渠道基土的冻胀是引起渠道衬砌板破坏的主要原因。国内许多学者和专家对渠道冻胀力学模型进行了大量的研究，取得了丰富的成果。王正中等[2-3]通过对渠道衬砌板受力的适当假设和简化分别建立了梯形和弧形底梯形渠道的冻胀力学模型。余书超等[4]通过研究板与冻土间的相互约束关系，合理地解释了边坡板在实际工程中沿斜坡整体上移和隆起架空的现象，并提出了寒区刚性护面渠道护砌层受冻胀时的内力计算方法。申向东等[5]将混凝土衬砌梯形断面渠道的预制板之间的连接方式简化为铰接，依据材料力学相关计算分析方法建立力学模型；宋玲等[6]依据桩的抗冻拔验算和拉弯构件的强度验算实现冬季输水渠道抗冻胀力的计算，为冬季输水梯形混凝土防渗抗冻胀渠道衬砌层厚度的准确确定提供了计算方法。李翠玲等[7-9]分别考虑到两拼式U形渠道和三板拼接式小型U形渠道混凝土衬砌的特殊受力情况，通过研究分析建立了其冻胀力学模型。

以往的渠道冻胀力学模型[2-9]将衬砌板简化为简支梁进行分析。简支梁冻胀模型简单，计算方便，但将衬砌板的两端看为铰支座进行分析，这与实际冻胀时衬砌板的被约束特点有所出入。将法向冻结力以集中力的方式施加于边坡衬砌板顶部，这与实际的受力状态有所不符。同时，最大切应力0根据公式0=+进行计算，系数和较难获得。

SL23-2006《渠系工程抗冻胀设计规范》[10]中详细推荐了不同地区、土质、地下水位、遮阴程度、渠道走向等因素的冻胀量计算方法，一定程度综合体现了设计渠道基土的冻胀特性。一些原型试验[11-15]也得到了渠道冻胀位移，其位移大小及分布对工程设计具有重要参考价值。因此，建立一个基于冻胀量计算的渠道混凝土衬砌冻胀力学模型，既与SL23-2006《渠系工程抗冻胀设计规范》有机衔接，也为寒区渠道抗冻胀设计提供参考。

弹性地基梁理论已广泛的应用在以冻土为基础的结构分析中，能较好体现建筑物与冻土之间相互作用。李方政[16]将非均布的冻胀荷载简化成多段均布荷载，编制MATLAB程序求解冻土地基上的弹性地基梁方程，得到冻胀与地基梁相互作用的位移及接触压力，并用实测数据验证其合理性。李晓丽等[17]利用弹性地基梁理论建立埋地管道在土体不均匀冻胀情况下的力学模型。黄龙等[18]基于弹性地基梁理论建立冻胀条件下的管-土相互作用模型，分析了管道在冻胀及其影响因素作用下的应力分布规律。管道和基土之间的相互作用，结构形式与渠道有着一定的区别，因此上述管道冻胀的弹性地基梁模型[17-18]并不能体现渠道冻胀特点。

肖旻等[19]基于冻胀力和冻胀强度成线性关系并结合弹性地基梁理论，建立了考虑冻土与结构相互作用的梯形渠道冻胀破坏弹性地基梁模型。但该模型依然采用简支梁模型的支承方式，将冻结力集中于边坡衬砌板的顶部进行分析，弱化了冻土与衬砌板的相互作用效应。

本文通过分析实际梯形渠道冻胀过程中混凝土衬砌板的受力变形特点，弥补简支梁模型不能体现渠道基土冻胀过程中混凝土衬砌板与基土之间相互作用的不足，在SL23-2006《渠系工程抗冻胀设计规范》推荐的冻胀量基础上，结合弹性地基梁理论建立梯形渠道混凝土衬砌冻胀力学模型，为寒区渠道抗冻胀设计提供参考。

1 梯形渠道混凝土衬砌冻胀弹性地基梁力学模型的建立

根据文献[20]，将梯形渠道的基土假设为刚性支座上的一系列相互独立、彼此不发生联系的弹簧，如图1a所示。冻胀量通过弹簧的伸长量体现，冻胀力通过弹簧被压缩产生的反力体现，如图1b所示。基于该假设构建梯形渠道混凝土衬砌冻胀的弹性地基梁力学模型。

注：A、D两点为边坡衬砌板顶点；B、C两点为渠道坡脚点。

1.1 基本假设及简化

1）渠道基土的冻胀效应等效为一组相互独立且垂直或平行于衬砌板的弹簧，冻胀量通过弹簧的伸长量体现，冻胀力通过弹簧被压缩产生的反力体现；

2）边坡衬砌板和渠底衬砌板之间的连接方式看作铰接；

3）在冻胀过程中认为渠基冻土和衬砌板之间始终冻结在一起，不发生相互脱离；

4）将法向冻胀力和法向冻结力统一看成基土冻胀时与衬砌板相互作用的冻胀反力()。当冻胀反力为压力时，为法向冻胀力；当冻胀反力为拉力时，为法向冻结力。

5）衬砌板上的切向冻结力()为冻土和衬砌板发生相互错动位移时，冻土与衬砌板接触面之间的粘结力，类似于一般土壤的粘聚力和内摩擦角概念，其大小与冻土的土质、温度、含水量、接触面粗糙度等相关。本文通过法向冻胀反力来综合体现冻土的物理特性，认为切向冻结力()与法向冻胀力()成正比，即

式中()为切向冻结力，Pa；()为冻胀反力，Pa；为比例系数，根据后续式（25）和式（26），并结合冻胀反力()进行计算。当()为正值时，其与衬砌板相互作用切向力方向相反；当()为负值时，其与衬砌板相互作用切向力方向相同。

6）边坡衬砌板和渠底衬砌板下的冻土均匀冻胀，不考虑由渠道基土不均匀冻胀引起的应力变化。

7）渠道建成后衬砌板的自重已和基础相互平衡，本文研究仅考虑基土冻胀后附加的冻胀力对衬砌板的作用，受力分析时不考虑渠道衬砌板自重对结构影响。

8）相对于衬砌板的长度，衬砌板厚度很小，故忽略切向冻结力产生的弯矩。

1.2 弹性地基梁力学模型的构建

基于Winkler模型的弹性地基梁基本微分方程[16-20]，并结合渠道冻胀弹性地基梁分析简图（图2），则渠道混凝土衬砌冻胀弹性地基梁基本微分方程为

式中为渠道基土冻胀时被约束住的冻胀量，m；为衬砌板的弹性模量，Pa；()为施加在衬砌板上的外部荷载，N；为冻胀力系数，N/m3；为衬砌板断面的惯性矩，m4，沿渠道走向取单位宽度的衬砌板进行分析，则=3/12，为衬砌板厚度，m。

注：为渠道基土冻胀时被约束住的冻胀量，m；为渠道基土在约束情况下发生冻胀的实际冻胀量，m；Δ为渠道基土未被约束时的自然冻胀量，m；()为施加在衬砌板上的外部荷载，N。

Note:is the amount of frost heave that is restrained when the channel base soil is frost heaving, m;is the actual frost heave of the channel base soil under the constraint condition, m; Δis the amount of natural frost heaving when the channel base soil is not constrained, m;() is the external load applied to the lining, N.

图2 渠道冻胀弹性地基梁分析简图

Fig.2 Analysis diagram of channel frost heave elastic foundation beam

根据文献[21]，渠基冻土的基床系数0与弹性模量E和泊松比的关系表示为

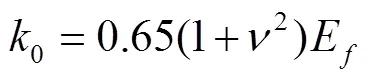
式中E为基土的弹性模量，Pa；为泊松比；0.65为经验系数。

渠道衬砌冻胀力系数与弹性地基梁理论中基床系数存在一定相似性，目前对基床系数的研究相对较多[22-25]，但冻胀力系数研究相对较少。冻胀力系数根据冻胀反力和被约束冻胀量进行计算。本文基于基床系数的研究成果，引入折减系数，将基床系数0和冻胀力系数联系起来，把基床系数0引入渠道冻胀分析中，因此对式（3）做如下修正：

式中为折减系数，≤1.0。根据本文力学模型，已有试验[11]和数值模拟[26]的结果对比，求得=0.4。

令

则式（2）可以写成

式（6）是一个四阶常系数线性非齐次微分方程。作用在基础梁上的外部荷载()为不超过三次的多项式时，其通解为[20]

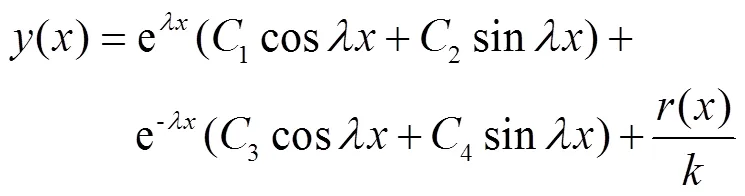
式中1、2、3和4是积分常数，根据基础梁的边界条件确定。

基于Winkler假定和式（7）计算出冻胀反力()为

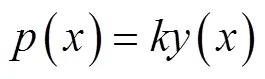
根据材料力学理论[27]得到衬砌弯矩()和剪力()计算式为

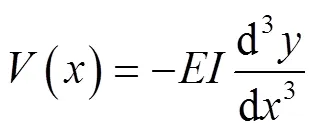
在弹性地基梁计算时，根据集中力或集中力偶作用点距梁端的距离将基础梁分为无限长梁、半无限长梁和短梁3种情况，根据文献[20]来判断基础梁的类型。

1）无限长梁——荷载作用点至梁两端的距离大于3，为特征长度，m；

2）半无限长梁——荷载作用点至梁一端的距离小于3，而至另一端的距离大于3；

3）短梁——荷载作用点至梁两端的距离均小于3。

基础梁的特征长度按式（11）计算[20]。

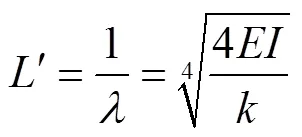
根据文献[20]，渠道基土的基床系数0为1.0×104～10.0×104kN/m3；渠道衬砌所用混凝土的强度等级一般采用C15和C20[28]，其弹性模量分别为2.20×104和2.55×104N/mm2[29]；渠道衬砌板厚度一般为0.05～0.20 m，所以有：

0.93 m≤3

L

′

≤4.84 m （12）

渠道衬砌板的长度因渠道内设计流量差异有很大不同，涵盖式（12）的全部范围。为使所得到的力学模型更具有普遍适用性，本文采用短梁的弹性地基梁计算理论构建梯形渠道混凝土衬砌冻胀力学模型。

1.2.1 边坡衬砌板弹性地基梁力学模型

根据图1b，在边坡衬砌板发生冻胀时，渠顶在渠道基土的冻胀作用下产生一定的冻胀位移，坡脚由于渠道底板的约束作用，其冻胀被约束。故对边坡进行单独分析时认为渠底受到一对来自底板的约束反力，如图3b所示。

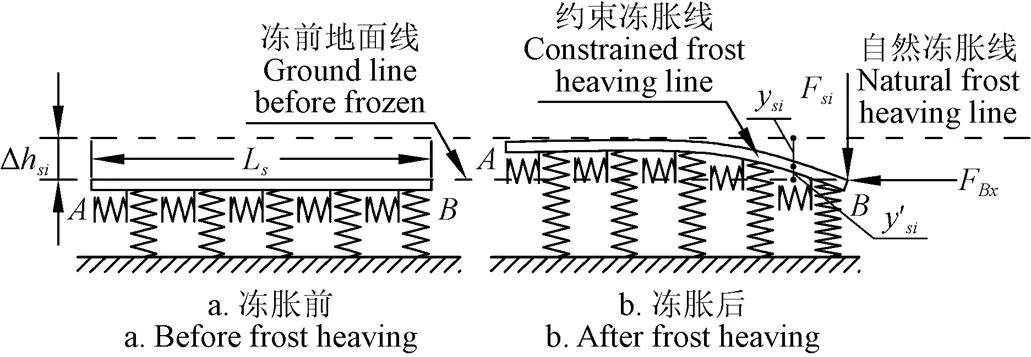
注：Ls为边坡衬砌板长度，m；Δhsi为边坡自然冻胀量，m；Fsi为边坡衬砌板在发生冻胀时受到底板约束的垂直于边坡衬砌板的约束反力，N；FBx为边坡衬砌板在发生冻胀时受到底板约束的平行于边坡衬砌板的水平约束反力，N；ysi为边坡衬砌板下基土冻胀时被约束住的冻胀量，m；y′si为边坡衬砌板下基土在约束情况下发生冻胀的实际冻胀量，m；i=1代表阴坡衬砌板，i=2代表阳坡衬砌板，下同。

首先对边坡衬砌板冻胀后的垂直方向受力情况进行分析，水平方向受力将在第1.3节根据力的平衡进行分析。

如图3b所示，将边坡衬砌板在垂直方向受力看成是集中力作用于短梁的端点。根据文献[20]中关于集中力作用短梁端点的计算理论可以得出边坡衬砌板在冻胀情况下的力学模型，其挠度y(,F)、弯矩M(,F)、剪力V(,F)和冻胀反力p(,F)分别为

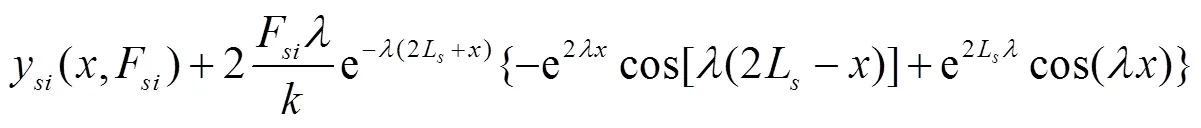
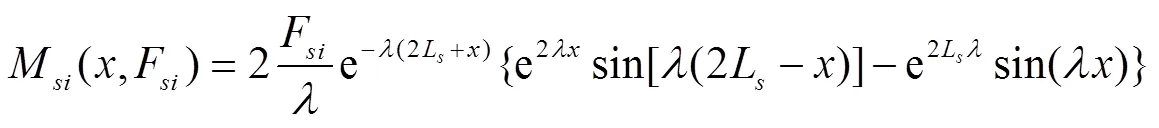
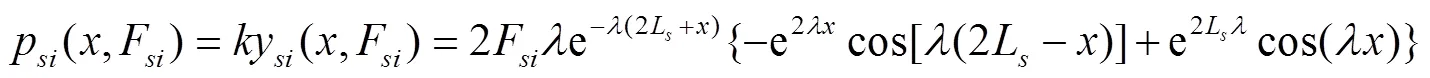
根据图3b，y(,F)是相对于自然冻胀线的位移挠度，一般研究的是相对于冻前地面线的位移挠度y′(,F)，故将式（13）做如下转换：

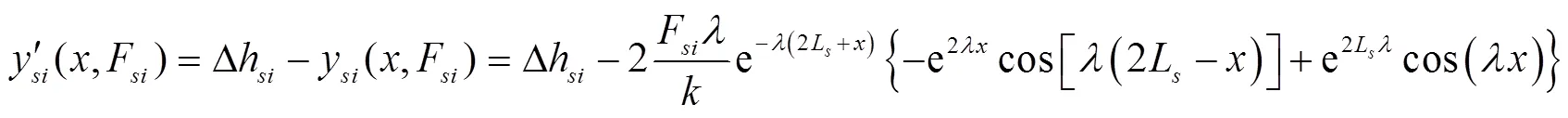
1.2.2 渠底衬砌板弹性地基梁力学模型

根据图1b，渠底衬砌板发生冻胀时，受到两边边坡衬砌板的约束，故渠底衬砌板两端受到来自边坡衬砌板的一对约束反力，如图4所示。

先对渠底衬砌板冻胀后的垂直方向受力情况进行分析，水平方向受力情况在第1.3节根据力的平衡进行分析。

求解该力学模型其实就是利用叠加法将2个短梁端点受集中荷载的模型进行叠加。根据叠加原理和式（13）～（16）求得

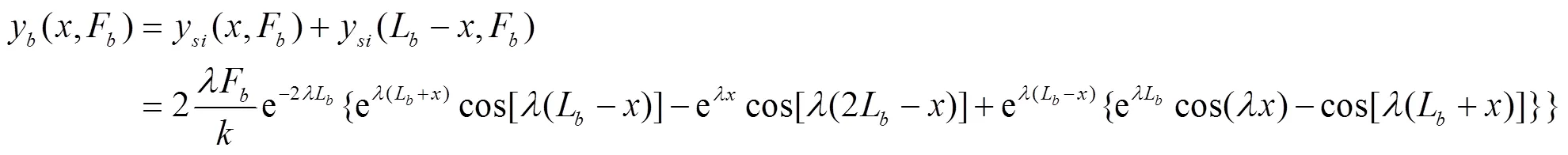
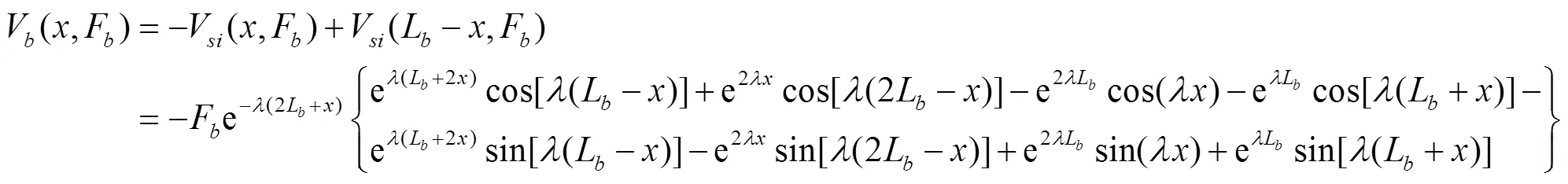
式中y(,F)、M(,F)、V(,F)和p(,F)分别为渠底衬砌板冻胀时的挠度(m)、弯矩(N∙m)、剪力(N)和冻胀反力(Pa)。

与边坡衬砌板同理，y(,F)是相对于自然冻胀线的挠度，将式（18）做如下变换：

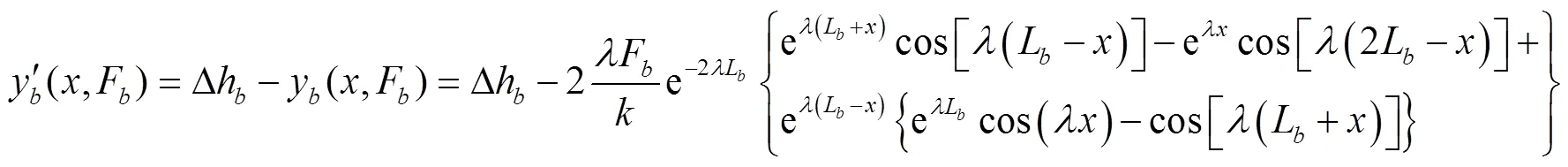
注：L为渠底衬砌板长度，m；Δh为渠底冻胀量，m；F为渠底衬砌板在发生冻胀时受到边坡衬砌板约束的垂直于底板的约束反力，N；F′和F′分别为渠底衬砌板在发生冻胀时受到阴坡和阳坡衬砌板约束的平行于底板的水平约束反力，N；y为渠底衬砌板发生冻胀后被约束住的冻胀量，N；′为渠底衬砌板发生冻胀后的实际冻胀量。

Note:Lis the length of the canal bottom lining plate, m; Δhis the amount of natural frost heaving of the bottom of the channel, m;Fis the restraining reaction force of the bottom lining plate which is restrained by the slope lining plate when the frost swell occurs, N;F′andF′are the horizontal restraining reaction forces which parallel to the bottom plate which are bound by the shady slope and the sunny slope lining plate when the frost swell occurs, N;yis the amount of frost heave that is restrained after frost heave of the bottom lining, N;′is the actual frost heave after frost heave of the bottom lining.

图4 渠底衬砌板冻胀弹性地基梁力学模型

Fig.4 Mechanical model of frost heaving elastic foundation beam of canal bottom lining plate

1.3 梯形渠道混凝土衬砌板冻胀力学平衡

如图5所示，边坡衬砌板在坡角约束反力F和F，冻胀反力p()与切向冻结力τ()共同作用下保持平衡。渠底衬砌板在坡角约束反力F、′和′，冻胀反力p()与切向冻结力τ()共同作用下保持平衡。以坡脚点力学平衡进行分析。点同理，故不再对其进行单独分析。

F和F与F和′在点是一对作用力与反作用力，则

垂直方向：

水平方向：

由边坡衬砌板切向静力平衡可知

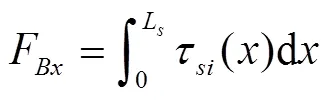
由渠底衬砌板切向静力平衡可知

混凝土衬砌板轴力计算：

边坡衬砌板：

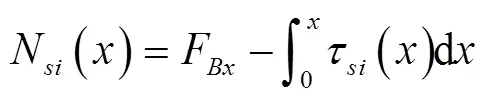
式中N()为边坡衬砌板轴力，N。

渠底衬砌板：

式中N()为边坡衬砌板轴力，N。

轴力为压力时是正值，为拉力时是负值。

1.4 计算流程

1）根据现场观测或SL23-2006《渠系工程抗冻胀设计规范》[10]确定阴坡、阳坡和渠底冻胀量Δ。

阴坡、阳坡和渠底的冻胀量Δ，对于1、2、3级渠道宜通过现场观测资料，按照工程建成后的温度、水分及运行条件进行修正后确定[10]。野外冻胀量的观测方法按SL237-1999《土工试验规程》[30]规定执行。对于4、5级渠道或没有现场试验观测条件的，根据SL23-2006《渠系工程抗冻胀设计规范》进行确定[10]。

2）将各个部位的冻胀量Δ带入式（17）和式（22），根据在=0处挠度为0计算出垂直约束反力F1，F和F2；

3）将垂直约束反力F1，F和F2分别带入式（14）～（17）和式（19）～（22），得到边坡和渠底衬砌板的冻胀后的挠度、冻胀反力、弯矩和剪力；

4）将垂直约束反力F1，F和F2带入式（23）和式（24）计算出F、F′、F和F′；

5）将F、F′、F和F′带入式（25）和式（26），并结合式（1），计算出边坡和渠底衬砌板切向冻结力；

6）将计算出的切向冻结力带入式（27）和式（28）求出边坡和渠底衬砌板的轴力；

7）根据文献[2]中关于渠道混凝土衬砌板破坏断裂计算方法，判断渠道冻胀时衬砌板是否发生破坏。

2 工程算例

以甘肃省靖会总干渠梯形渠道为例，对本文建立的力学模型进行验证。该渠道的断面尺寸如图6所示。由于渠道各部位的坡向不同，日照及遮阴程度不一，以及土质、水分、风力等条件的差异，加之渠道走向不同，因而各部位的日照及温度水分状况不同，冻结状态及冻深也不同，基本冻胀情况见表1。渠道基础冻土弹性模量为46MPa，泊松比为0.33[26]；衬砌板所用混凝土的弹性模量为24GPa[26]。

注：图中尺寸单位为m。

表1 原型渠道基本冻胀情况[11]

将表1中的冻胀量Δ分别带入式（17）和式（22），计算结果为

将上述计算结果分别带入式（14）～（17）和式（19）～（22）得到边坡和渠底衬砌板的冻胀量、冻胀反力、弯矩和剪力。

关于甘肃省靖会总干渠，李安国等[11]通过缩小模型对该渠道进行试验提出了模型试验结果能较好地反映原型渠道的冻胀、冻结特征和规律、模型与原型的冻深、冻胀量呈线性相关。李爽等[26]结合该试验的结果，对该渠道进行考虑混凝土衬砌板与冻土接触非线性的数值模拟。肖旻等[19]对边坡衬砌板两端约束简化为简支，基于弹性地基梁理论，建立考虑冻土与结构相互作用的梯形渠道冻胀破坏力学模型。为验证本文模型合理性，将本文模型计算结果与文献[11]，文献[19]和文献[26]进行比较分析，结果见图7和图8所示。

2.1 冻胀量分析

图7a为冻胀量沿渠道断面展开长度的分布。由图7a可以看出，本文模型所计算的冻胀量分布规律和文献[11]、文献[26]的基本一致。由于数值模拟[26]结果需要用到许多力学参数，其量值与实际存在差异，但总体规律是一致的，故本文与文献[26]进行冻胀量和冻胀反力的分布规律进行比较，关键点的冻胀量与试验结果[11]进行比较。考虑到文献[11]的试验误差，试验结果的冻胀量分布规律不是太好，因此以渠道各个部位平均冻胀量综合分析本文模型的合理性，其相对平均误差如表2所示。

由图7a可知，和文献[11]相比，本文模型计算的冻胀量沿渠道断面展开长度的分布规律和试验结果基本一致，其中观测点②、③、④、⑥、⑧和⑨处的结果基本吻合，但和试验[11]观测点①和观测点⑦结果相差较大，这不排除试验[11]误差带来的影响。总体上，本文模型计算的边坡冻胀量从坡脚到坡顶逐渐变大，在距坡脚三分之一左右处达到最大值，阳坡最大冻胀量为5.3 cm，阴坡最大冻胀量为3.9 cm，冻胀量随着展开长度的增加开始缓慢减小，渠底冻胀量在中部达到最大值3.8 cm，这一规律和数值模拟结果[26]基本一致。从图7a中文献[19]的计算可以看出，其渠底和边坡下半部分的冻胀量计算结果分布规律与实测结果[11]基本吻合，但由于其在边坡衬砌板分析时，将两端约束简化为简支，导致阴坡和阳坡的衬砌板顶部计算冻胀量为0，这与文献[11]的试验结果不符，而本文克服了简支边界条件的不足，且基于已知的自然冻胀量建立弹性地基梁模型，较文献[19]能更好地反映边坡衬砌板的冻胀规律。

由表2可以看出，本文模型的冻胀量计算值和文献[11]的试验结果平均相对误差较小，整体平均相对误差为4.72%，各个部位的相对平均误差均在允许范围之内，因此本文模型相对合理。但阳坡的误差相对较大，这不排除观测点⑦试验误差带来的影响。

表2 本文模型冻胀量计算值与文献[11]试验结果的相对误差

2.2 冻胀反力分析

图7b为冻胀反力沿渠道截面展开长度的分布。由图7b可见，本文模型计算的冻胀反力分布规律和文献[26]数值模拟结果基本一致。在坡脚处，由于边坡衬砌板和渠底衬砌板的相互约束作用，冻胀量为0，产生的法向冻胀力最大。在阴坡坡脚，本文模型计算的法向冻胀力平均值为0.61 MPa，数值模拟结果为0.56 MPa[26]，本文模型比数值模拟[26]结果大8.9%；在阳坡坡脚，本文模型计算的法向冻胀力平均值为0.52 MPa，数值模拟[26]结果为0.38 MPa，本文模型比数值模拟[26]结果大36.8%。可以看出本文模型在阳坡坡脚处所计算出的冻胀反力和数值模拟[26]结果相差较大，这是由于本文模型将渠道混凝土衬砌板下的冻土的冻胀力系数看为恒定值，忽略因渠道边坡差异对冻胀力系数的影响，故阳坡坡脚处的冻胀反力和数值模拟[26]结果相差较大。

在渠底中部由于衬砌板和冻土相互作用产生较大的冻胀位移，应力得到一定释放，相对于底板其他地方，中部法向冻胀力最小，为0.20 MPa。在边坡上部三分之二区域，本文模型计算结果存在法向冻结力，在下部三分之一区域存在法向冻胀力，这与数值模拟的结果基本一致。机理分析如下，边坡衬砌板在发生冻胀时，坡脚处受来自底板的约束，使该处和其临近区域的冻胀变形受到约束，因而产生很大的冻胀力。在该冻胀力的作用下，边坡衬砌板的中部和上部有向外翘的趋势。由于冻土和衬砌板紧紧的冻结在一起，故在边坡衬砌板的中部和上部产生一定的法向冻结力。

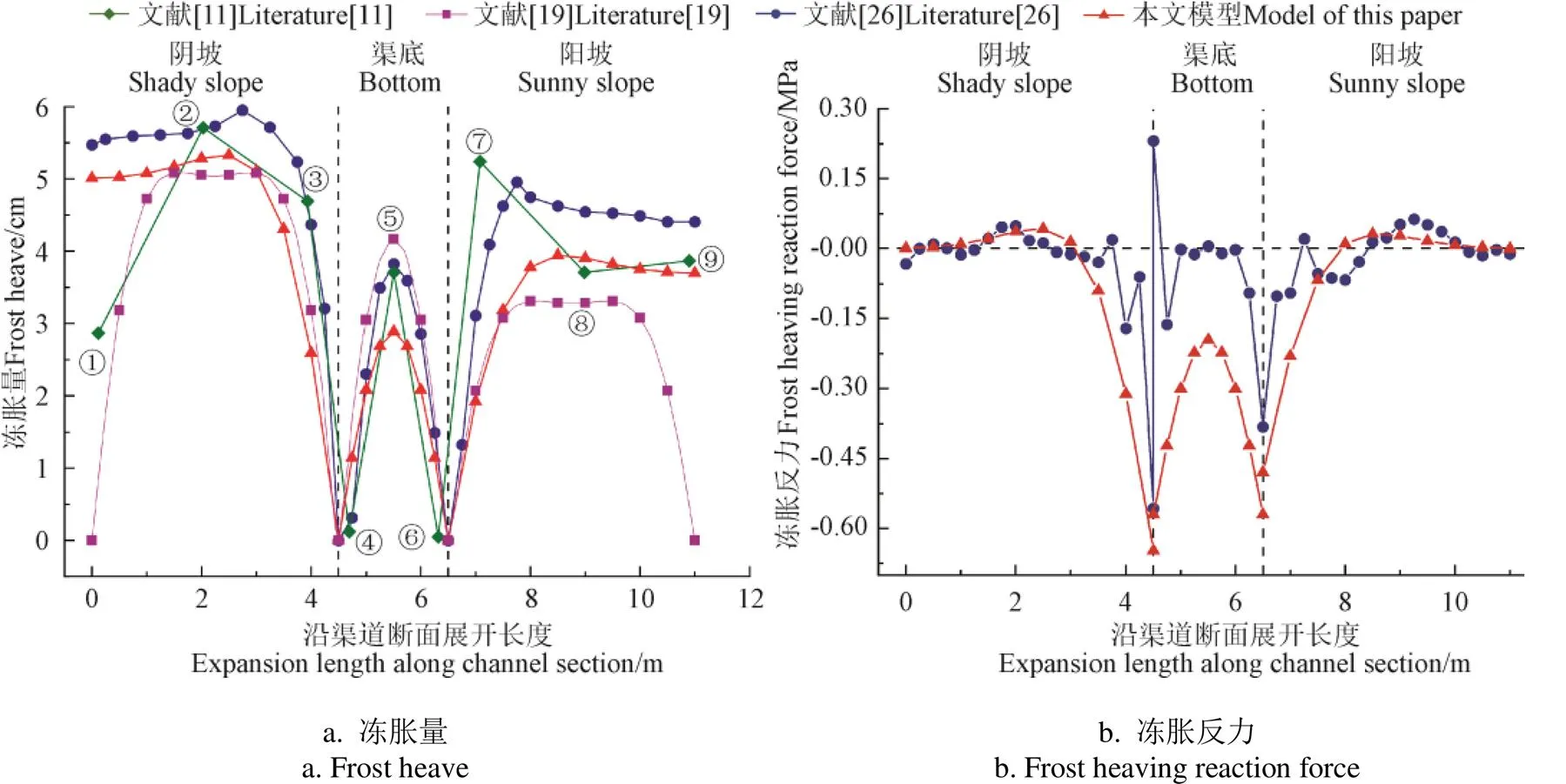
注：冻胀反力为正时为法向冻结力，为负时为法向冻胀力；图中编号为文献[11]试验观测点编号。

2.3 弯矩分析

图8a为衬砌板弯矩分布图。由图8a可见，在渠底中部弯矩最大，这和以往力学模型计算结果的分布规律基本一致。但边坡的弯矩最大值82 kN∙m距坡脚五分之一左右处，这和以往的力学模型的三分之一左右有所不同，但总体分布规律一致。这是因为将冻土看为完全弹性体，而忽略冻土塑性变形对冻胀力的消减作用，计算出来坡脚区域的法向冻胀力较大，使弯矩最大值点向坡脚偏移而导致的结果。

2.4 剪力分析

图8b为衬砌板剪力分布图。由图8b可见，在坡脚处，由于边坡和渠底冻胀时的相互约束而产生很大的冻胀力，因此在坡脚处的剪力较大。在渠顶的剪力分布和简支梁力学模型有所不同。在简支梁模型中，边坡顶部会出现剪力极值，这是由于在简支梁模型中将法向冻结力以集中力的形式作用于边坡顶部而产生的。在弹性地基梁模型中用冻土和基础相互作用计算出法向冻结力的分布，并由图7b可以看出法向冻结力在边坡上三分之二区域分布，在坡顶为0，因此该处的剪力为0。可以看出本文模型所计算出衬砌板剪力分布和实际更为相符。

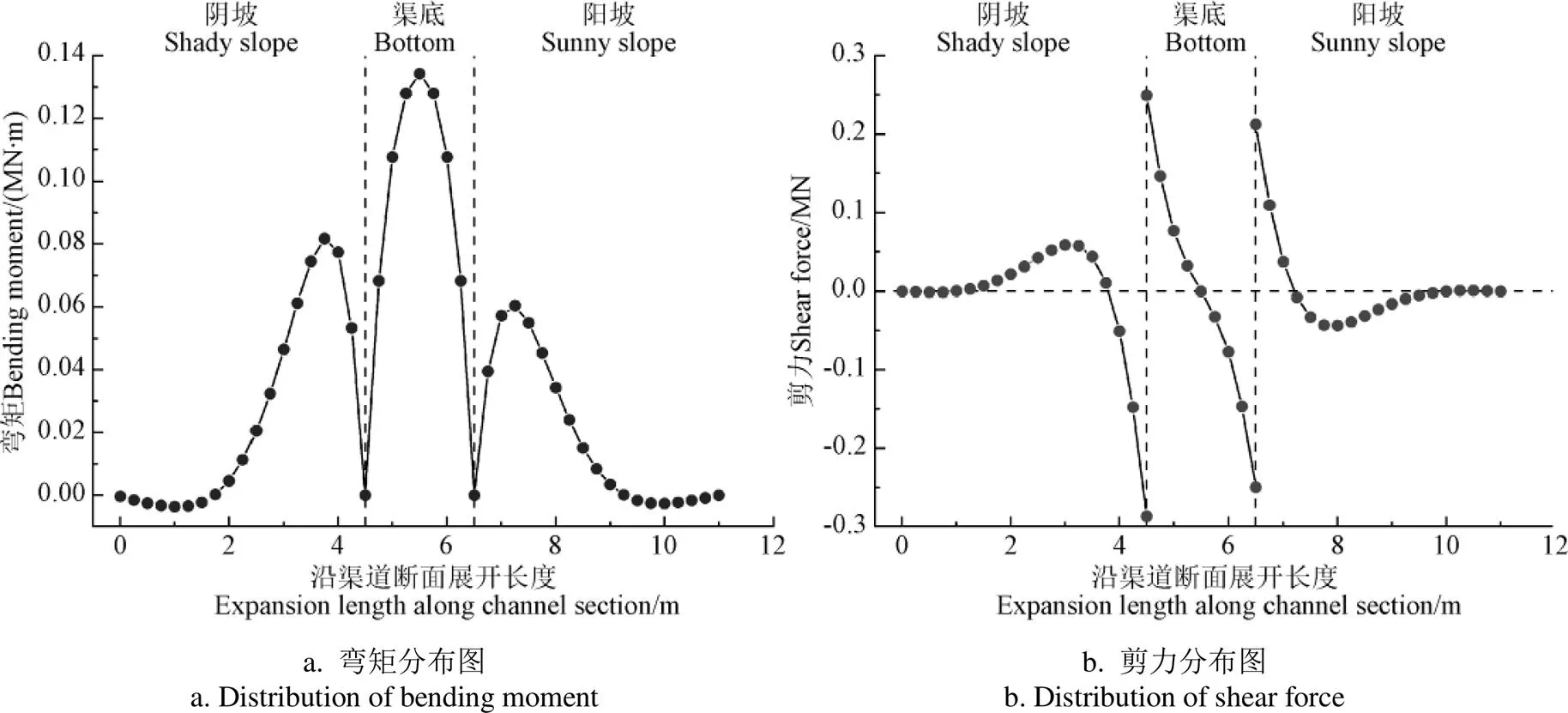
图8 渠道衬砌板内力分布图

3 结 论

1）本文模型抛弃了将衬砌板简化为两端简支的边界条件，直接根据渠道衬砌板在冻胀过程中的受力变形协调性建立边界条件。基于自然冻胀量，根据弹性地基梁理论进行求解，得到的冻胀量和冻胀反力的分布规律与实际更为相符。推导出冻胀后的衬砌板的冻胀量、冻胀反力、弯矩和剪力分布的解析表达式，并通过梯形渠道衬砌板冻胀力学平衡给出了切向冻结力和轴力的计算方法。

2）以甘肃省靖会总干渠梯形渠道为例，通过本文模型计算的冻胀量和冻胀反力的分布规律与前人的试验和数值模拟进行对比，分布规律基本一致。同时，本文模型计算的冻胀量和试验结果的平均相对误差为4.7%，证明了其合理性。

3）本文模型考虑SL23-2006《渠系工程抗冻胀设计规范》关于冻胀量的计算成果，建立了基于冻胀量的力学模型，既与规范有机衔接，也为寒区渠道抗冻胀设计提供参考。

本文假设渠道混凝土衬砌板下的冻土为完全弹性体，并没有考虑其塑性变形对冻胀力的消减作用，故计算出的冻胀力偏大。同时，本文假设冻胀时由于边坡和渠底衬砌板之间的相互约束作用，坡脚处的冻胀量完全被约束，这与实际情况可能有所不符。若要考虑以上2点对渠道冻胀带来的影响，仍有待进一步研究。

[1] Zhao Lin, Cheng Guodong, Ding Yongjian. Studies on frozen ground of China[J]. Journal of Geographical Sciences, 2004, 14(4): 411－416.

[2] 王正中. 梯形渠道砼衬砌冻胀破坏的力学模型研究[J]. 农业工程学报，2004，20(3)：24－29. Wang Zhengzhong. Estabishment and application of mechanics model of frost heaving damage of concrete lining trapezoidal open canal[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2004, 20(3): 24－29. (in Chinese with English abstract)

[3] 王正中，李甲林，陈涛，等. 弧底梯形渠道砼衬砌冻胀破坏的力学模型研究[J]. 农业工程学报，2008，24(1)：18－23. Wang Zhengzhong, Li Jialin, Chen Tao, et al. Mechanics models of frost-heaving damage of concrete lining trapezoidal canal with arc-bottom[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(1): 18－23. (in Chinese with English abstract)

[4] 余书超，欧阳辉，孙咏梅. 渠道刚性衬砌受冻胀时的内力计算[J]. 中国农村水利水电，1999(10)：21－23. Yu Shuchao, Ouyang Hui, Sun Yongmei. Experimental research on stressing status of rigidlining of canal sunder frost upheaval[J]. China Rural Water and Hydropower, 1999(10): 21－23. (in Chinese with English abstract)

[5] 申向东，张玉佩，王丽萍. 混凝土预制板衬砌梯形断面渠道的冻胀破坏受力分析[J]. 农业工程学报，2012，28(16)：80－85. Shen Xiangdong, Zhang Yupei, Wang Liping. Stress analysis of frost heave for precast concrete panel lining trapezoidal cross-section channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(16): 80－85. (in Chinese with English abstract)

[6] 宋玲，欧阳辉，余书超. 混凝土防渗渠道冬季输水运行中冻胀与抗冻胀力验算[J]. 农业工程学报，2015，31(18)：114－120. Song Ling, Ouyang Hui, Yu Shuchao. Frozen heaving and capacity of frozen heaving resistance of trapezoidal concrete lining canal with water in winter[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(18): 114 －120. (in Chinese with English abstract)

[7] 李翠玲，王红雨. 两拼式U形渠道混凝土衬砌结构冻胀破坏力学模型[J]. 中国农村水利水电，2014(5)：86－93. Li Cuiling, Wang Hongyu. Mechanics model of frost-heaving damage of concrete lining U-shaped canals with splicing two arc-plates[J]. China Rural Water and Hydropower, 2014(5): 86－93. (in Chinese with English abstract)

[8] 王江伟，王红雨. 考虑土与板间摩擦力的两拼式U形复合衬砌渠道冻胀破坏力学模型[J]. 中国农村水利水电，2016(5)：145－149. Wang Jangwei, Wang Hongyu. Frost heaving mechanics model of composite lining U-shaped canals considering interface friction from soil, geo-membrane and splicing double arc-plates[J]. China Rural Water and Hydropower, 2016(5): 145－149. (in Chinese with English abstract)

[9] 唐少容，王红雨. 三板拼接式小型U形混凝土衬砌渠道冻胀破坏力学模型[J]. 农业工程学报，2016，32(11)：159－166. Tang Shaorong, Wang Hongyu. Mechanical model of small U-shaped concrete lining canal with three arc-plates under frost heaving[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(11): 159－166. (in Chinese with English abstract)

[10] 中华人民共和国水利部. 渠系工程抗冻胀设计规范，SL23-2006[S]. 北京：中国水利水电出版社，2006：9.

[11] 李安国，陈瑞杰，杜应吉，等. 渠道冻胀模拟试验及衬砌结构受力分析[J]. 防渗技术，2000，6(1)：5－16. Li Anguo, Chen Ruijie, Du Yingji. Simulation test of canal frost heave and stress analysis of lining structure[J]. Technology of Seepage Control, 2000, 6(1): 5－16. (in Chinese with English abstract)

[12] 姜海波，田艳. 季节冻土区刚柔混合衬砌梯形渠道冻胀机理试验[J]. 农业工程学报，2015，31(16)：145－151. Jiang Haibo, Tian Yan. Test for frost heaving damage mechanism of rigid-soften composite trapezoidal canal in seasonally frozen ground region[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(16): 145 －151. (in Chinese with English abstract)

[13] 李卓，盛金保，刘斯宏，等. 土工袋防渠道冻胀模型试验研究[J]. 岩土工程学报，2014，36(8)：1455－1463. Li Zhuo, Sheng Jinbao, Liu Sihuang, et al. Model tests on frost heave-prevented channels using soilbags[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(8): 1455－1463. (in Chinese with English abstract)

[14] 郭富强，史海滨，程满金，等. 不同地下水位下渠基冻胀规律与保温板适宜厚度确定[J]. 农业工程学报，2018，34(19)：95－103. Guo Fuqiang, Shi Haibin, Cheng Manjin, et al. Law of frost heave of canal foundation and appropriate thickness of insulation board under different groundwater levels[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(19): 95－103. (in Chinese with English abstract)

[15] 王羿，王正中，刘铨鸿，等. 寒区输水渠道衬砌与冻土相互作用的冻胀破坏试验研究[J]. 岩土工程学报，2018，40(10)：1799－1808. Wang Yi, Wang Zhengzhong, Liu Quanhong, et al. Experimental investigations on frost damage of canals caused by interaction between frozen soils and linings in cold regions[J].Chinese Journal of Geotechnical Engineering, 2018, 40(10): 1799－1808. (in Chinese with English abstract)

[16] 李方政. 土体冻胀与地基梁相互作用的叠加法研究[J]. 岩土力学，2009，30(1)：79－85. Li Fangzheng. Research on superposition method of interaction between soil frost heave and beams on foundation[J]. Rock and Soil Mechanics, 2009, 30(1): 79－85. (in Chinese with English abstract)

[17] 李晓丽，李廷辉，李满利，等. 非均匀冻胀对埋地管道结构安全性的影响[J]. 压力容器，2016，33(9)：64－70. Li Xiaoli, Li Yanhui, Li Manli, et al. Nonuniform frost heaving effect on buried pipeline structure safety[J]. Pressure Vessel Technology, 2016, 33(9): 64－70. (in Chinese with English abstract)

[18] 黄龙，盛煜，胡晓莹，等. 基于弹性地基梁理论的冻胀作用下管道应力分析[J]. 冰川冻土，2018，40(1)：70－78. Huang Long, Sheng Yu, Hu Xiaoying, et al. Stress analysis of pipelines subjected to frost heave based on the theory of elastic foundation beam[J]. Journal of Glaciology and Geocryology, 2018, 40(1): 70－78. (in Chinese with English abstract)

[19] 肖旻，王正中，刘铨鸿，等. 考虑冻土与结构相互作用的梯形渠道冻胀破坏弹性地基梁模型[J]. 水利学报，2017，48(10)：1229－1239. Xiao Min, Wang Zhengzhong, Liu Quanhong, et al. Elastic foundation beam model of frost heave damage of trapezoidal canal considering interaction between frozen soil and lining structure[J]. Journal of Hydraulic Engineering, 2017, 48(10): 1229－1239. (in Chinese with English abstract)

[20] 郭继武. 地基基础设计简明手册[M]. 北京：机械工业出版社，2007.

[21] Herrmann L R, Fletcher D Q. Elastic foundation representation of continuum[J]. Journal of Engineering Mechanics Division, ASCE, 1971, 97: 95－107.

[22] 仲锁庆，张西平，潘海利. 地基土基床系数研究[J]. 地下空间与工程学报，2005(S1)：131－134. Zhong Suoqing, Zhang Xiping, Pan Haili. Study on foundation soil coefficient of subgrade reaction[J]. Chinese Journal of Underground Space and Engineering, 2005(S1): 131－134. (in Chinese with English abstract)

[23] 周宏磊，张在明. 基床系数的试验方法与取值[J]. 工程勘察，2004，(2)：11－15. Zhou Honglei, Zhang Zaiming. Testing method and values of coefficient of subgrade reaction[J]. Geotechnical Investigation and Surveying, 2004, (2): 11－15. (in Chinese with English abstract)

[24] 于永堂，唐浩. 西安黄土基床系数变化规律及其测试方法的相关性分析[J]. 岩石力学与工程学报，2017，36(10)：2563－2571. Yu Yongtang, Tang Hao. Reaction coefficient of subgrade on Xi’an loess and correlation analysis of methods of measurement[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(10): 2563－2571. (in Chinese with English abstract)

[25] 塞尔瓦杜雷A P S. 土与基础相互作用的弹性分析[M]. 北京：中国铁道出版社，1984.

[26] 李爽，王正中，高兰兰，等. 考虑混凝土衬砌板与冻土接触非线性的渠道冻胀数值模拟[J]. 水利学报，2014，45(4)：497－503. Li Shuang, Wang Zhengzhong, Gao Lanlan, et al. Numerical simulation of canal frost heaving considering nonlinear contact between concrete lining board and soil[J]. Journal of Hydraulic Engineering, 2014, 45(4): 497－503. (in Chinese with English abstract)

[27] 孙训方，方孝淑，关来泰. 材料力学（Ⅰ）[M]. 第5版.北京：高等教育出版社，2009.

[28] 中华人民共和国水利部. 渠道防渗工程技术规范：GB/T50600-2010[S]. 北京：中国计划出版社，2011：1.

[29] 中华人民共和国水利部. 水工混凝土结构设计规范：SL191-2008[S]. 北京：中国水利水电出版社，2008：11.

[30] 中华人民共和国水利部. 土工试验规程：SL237-1999[S]. 北京：中国水利水电出版社，1999：3.

Frost heave mechanical model of concrete lining trapezoidal canal based on elastic foundation beam theory

Li Zongli1,2, Yao Xiwang1, Yang Le1, Shao Huajian1, Wang Zhengzhong1,2

(1.,,712100,; 2.,,712100,)

Frost heaving damage is the main way for channel lining damage in cold regions. It is a basic work to build a rational mechanical model of frost heaving for the anti-freeze design of channel lining. Based on Winkler's assumption, this paper considers that the frost heave effect of the foundation soil of channel is equivalent to a set of springs which are independent of each other and are vertical or parallel to the lining board. The amount of frost heaving is reflected by the elongation of the springs. The frost heave force is reflected by the reaction force generated by the compression of the springs. The frost heave mechanics model of concrete lining plate of trapezoidal channel is established based on the elastic foundation beam theory. It abandons the boundary condition of simplifying the lining board to the simple support at both ends, and directly establishes the boundary condition according to the coordination of the force and deformation of the channel lining plate in the frost heaving process, and applies the calculation result of frost heaving amount of the SL23-2006 “Specification for Design of Anti-freeze of Canal Engineering”. By analyzing the force characteristics during the frost heaving process of the channel lining plate, it is considered that the top of the slope lining plate will produce a certain frost heave displacement when the channel foundation soil is frost heaving. The frost heave at the end of the slope lining plate is restrained due to the bottom lining plate. Therefore, when the slope lining board is separately analyzed, it can be considered that the end of the slope lining plate is subjected to a pair of restraining reaction forces from the bottom plate. When the bottom lining plate is frost heave, the frost heaving at both ends of the bottom lining plate is restrained due to the two slope lining plate. Therefore, the two ends of the bottom lining are respectively subjected to a pair of restraining reaction forces from the slope lining plate. Applying the "short beam" theory of elastic foundation beams, the analytical expressions of frost heave amount, frost heave reaction force, bending moment and shearing force of the channel lining board after frost heaving are derived, and the calculation methods of tangential freezing force and axial force is given by the frost heave mechanical balance of trapezoidal channel lining board. Taking the trapezoidal channel of the main canal of Jinghui in Gansu Province as an example, the frost heave and frost heave reaction calculated by the model of this paper are compared with the previous experiment and numerical simulation, which the regularities of distribution is basically the same. Meanwhile, the overall average relative error of the frost heave amount obtained by this paper model is 4.72% compared with the results of the previous experiment, in which the rationality of the model is verified. The model of this paper applies the frost heave amount obtained from the SL23-2006 “Specification for Design of Anti-freeze of Canal Engineering”, which is organically linked with the design specification, and provides a reference for the anti-freeze design of canal in cold regions.

canals; frozen soils; displacement; elastic foundation beam; mechanical model

10.11975/j.issn.1002-6819.2019.15.015

TV91; TU445

A

1002-6819(2019)-15-0110-09

2019-03-18

2019-07-01

国家重点研发计划“高寒区长距离供水工程能力提升与安全保障技术”（2017YFC0405101-2）

李宗利，教授，博士生导师。主要从事水工结构设计理论与材料方面研究。Email：bene@nwsuaf.edu.cn

李宗利，姚希望，杨 乐，邵化建，王正中. 基于弹性地基梁理论的梯形渠道混凝土衬砌冻胀力学模型[J]. 农业工程学报，2019，35(15)：110－118. doi：10.11975/j.issn.1002-6819.2019.15.015 http://www.tcsae.org

Li Zongli, Yao Xiwang, Yang Le, Shao Huajian, Wang Zhengzhong. Frost heave mechanical model of concrete lining trapezoidal canal based on elastic foundation beam theory[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(15): 110－118. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.15.015 http://www.tcsae.org