高精度一体化PGK控制算法的仿真设计与实现*
2019-09-23彭俊然邓健辉杨世武
彭俊然 陈 庆 邓健辉 杨世武 李 闯
1.华中科技大学,武汉430074 2.中国航天科技集团烽火机械厂, 成都 611130
精确制导武器是目前国际上高科技武器研究的热点趋势之一,采用精确制导技术的各类制导武器比起普通弹道导弹,具有打击准确度高,附带毁伤低等特点,具有极高的军事应用前景[1]。传统的战术导弹控制系统中,控制器和导引率的设计往往是分开进行的,两者间缺少协调性,系统抵抗外界干扰或条件变化的能力较差[2]。近年来,制导和控制一体化的设计逐渐成为制导控制系统的主流[3-6]。一体化设计能够使得制导和控制有机统一,在达到更高的制导品质的同时,使得系统模型更为复杂,增加了系统中变量的不确定性[7]。因此对于一体化设计的硬件而言,其制导导引算法及修正控制对实现高精度投射至关重要。众多国内外学者对于制导导引算法进行了深入的研究。文献[8]采用模糊控制对摄动制导诸元进行解算并显著缩短了计算时间。文献[9]采用多项式拟合的方式进行路线制导。文献[10]采取重力补偿和加速度补偿修正比例导引,保证了制导精度。文献[11]以带重力补偿的比例导引律为基础,设计了基于变参数滑模调节项和视线偏差比例项组成的落角约束变结构偏置项,构成了比例导引加偏置项形式的末制导律。针对一体化的PGK硬件设计,选取模型简单,计算量小,且工程上易于实现的摄动制导方式设计了适用于它的控制算法,并在试验过程中对控制算法进行了优化。
1PGK控制系统的架构
1.1 PGK硬件组成
精确制导组件(Precision Guidance Kit, PGK)是辅助弹道导弹,提升其打击精度的核心组件。PGK通过GPS接收器计算导弹当前位置以及导弹的预计轨迹,并将计算结果与目标坐标进行对比,从而得到预定落点与实际目标之间的偏差,通过控制鸭翼外壳的转速与滚转方位对弹道进行修正,最终引导导弹沿更加准确的弹道飞向目标位置[12]。PGK组件主要包括头部组件和尾部组件2部分,分别位于整个系统的前端和后端,它们之间由前轴承和后轴承连接。尾部组件外部具有螺纹,可旋入标准螺纹孔与导弹固连。头部组件表面有一套固定安装角的气动面,一共包括4个小型的鸭舵片,两相邻舵片之间以90°间隔分布,相隔180°的2舵片被视为一对,执行相同的功能。头部组件还包括控制电路板,其
中包含卫星接收机、电机控制电路、数据记录模块以及用于计算导弹落点及其它弹道信息的弹载计算机电路和相应的控制组件。PGK组件结构如图1所示。

图1 PGK组件结构组成图
1.2 PGK控制系统结构
PGK控制系统采用固定翼滚转控制的单通道控制体制。导航方案采用“卫星导航+地磁滚转姿态测量”的方案,制导方案采用全程摄动制导,控制系统结构框图如图2所示。

图2 控制系统结构框图
1.2.1 导航系统
导航系统需要解算修正弹位置、速度信息和滚转姿态信息。位置、速度信息通过GPS导航卫星实时获取,滚转姿态通过弹上捷联的地磁敏感器件测量值和地磁场之间的夹角获取。导航系统框图如图3所示。

图3 导航系统框图
1.2.2 制导系统
PGK修正弹采用二维弹道修正方法提高无控弹的打击精度。全程弹道分为无控段、修正段和伞降回收段,仅在修正段进行制导修正。为提高修正能力,根据预装定时间,在弹道上升阶段进入修正段。
修正段采用摄动制导方案,卫星定位系统实时提供修正弹坐标和速度信号,姿态测量系统提供弹体转速、滚转角信号,弹载计算机综合飞行参数和预装摄动参数计算修正弹落点,并求得与目标之间的落点偏差(包括纵向偏差ΔL和横向偏差ΔH)。根据偏差生成摄动制导指令,控制PGK组件固定在指令滚转角上。修正段控制流程如图4所示。

图4 修正段控制流程图
1.2.3 鸭翼滚转角控制系统
鸭翼滚转角控制系统根据制导指令控制鸭翼的转速和滚转位置,通过调节外接电阻,改变电磁转矩的大小,控制鸭翼外壳的转速,并通过滚转角反馈(地磁模块)控制鸭翼外壳的滚转方位。系统控制框图见图5所示。
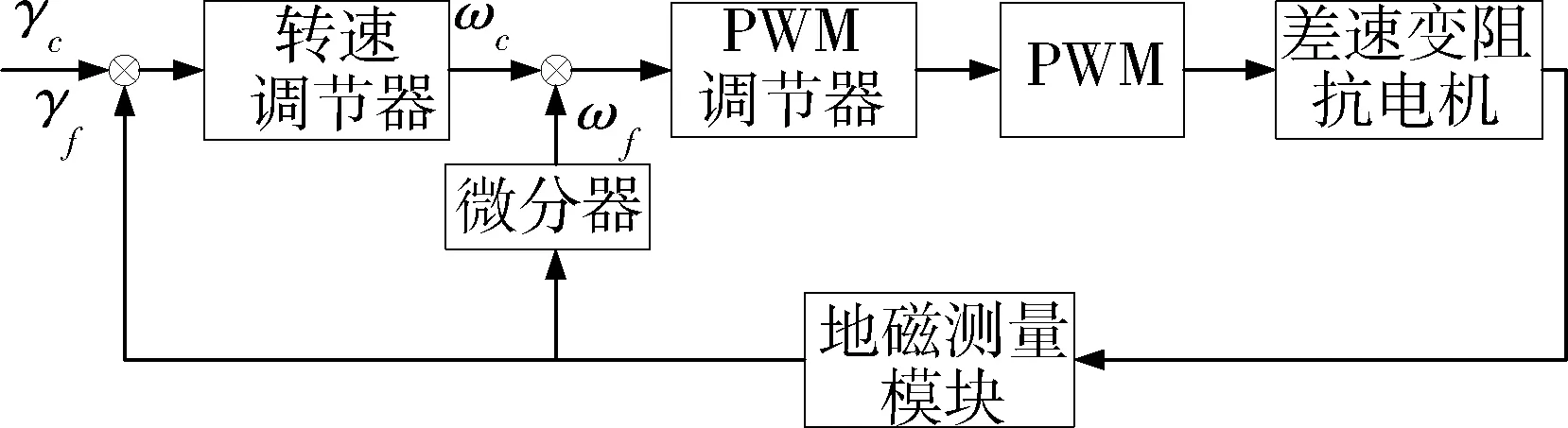
图5 鸭翼滚转角控制系统框图
2PGK制导算法
2.1 制导控制一体化模型的建立
2.1.1 位置、速度从地球坐标系转换到发射坐标系
速度矢量从地球坐标系(WGS-84系)到发射坐标系的计算公式为:
(1)
位置坐标分量从地球坐标系(WGS-84系)到发射坐标系的计算公式为:
(2)
弹道倾角、弹道偏角的计算公式为:
(3)
(4)
式中:xe,ye,ze,Vxe,Vye和Vze为GPS导航数据中的三向位移和速度;x,y,z,Vx,Vy和Vz为发射坐标系中的三向位移和速度;θ和σ表示弹道倾角和偏角。
2.1.2 导弹、目标点相对运动方程
记xr,yr和zr为目标点相对导弹的位置矢量,则有:
(5)
记vxr,vyr和vzr为目标点相对导弹的速度矢量,则有:
(6)

2.2 控制算法指令生成
2.2.1 GPS可用性判断
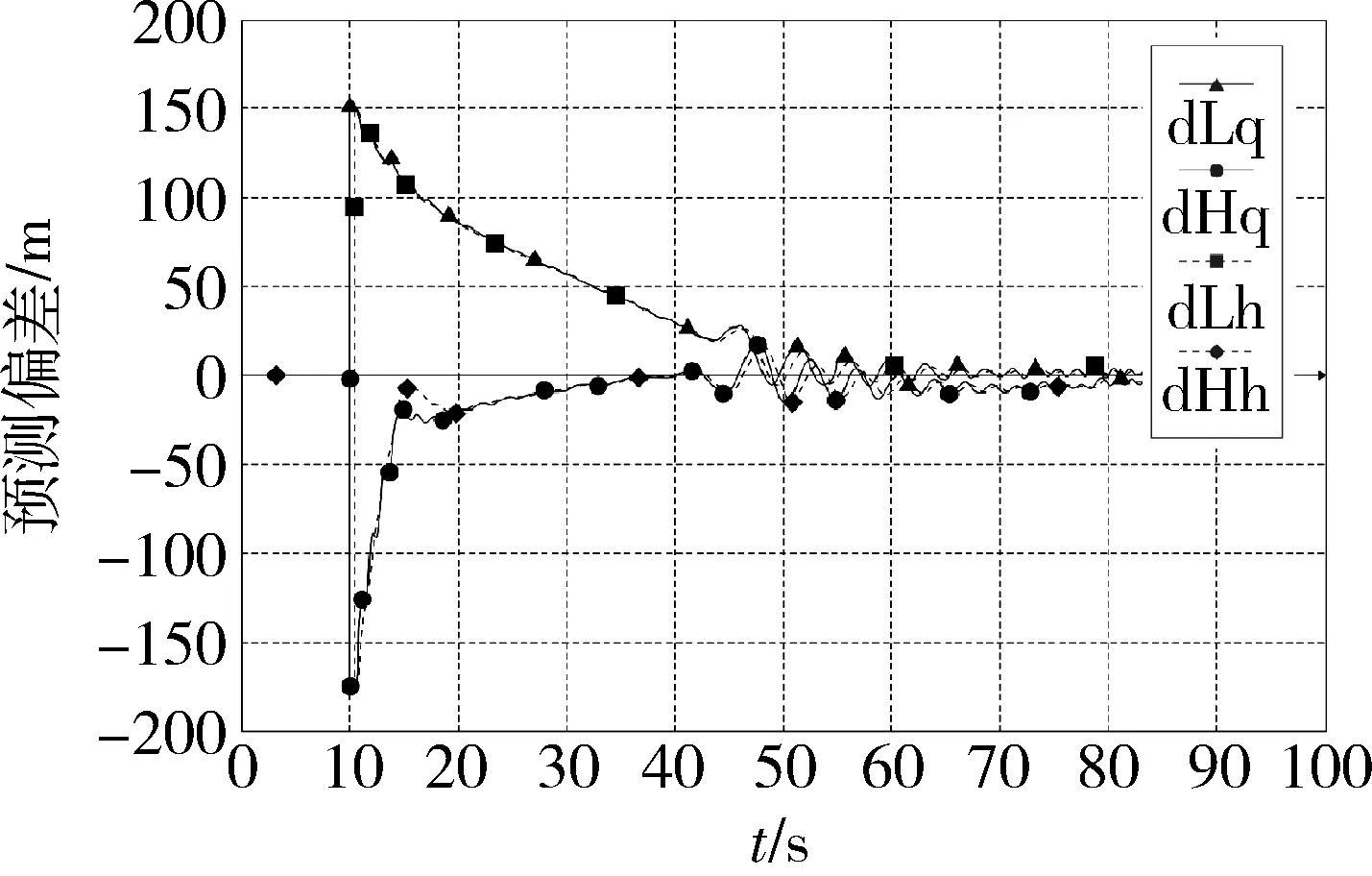
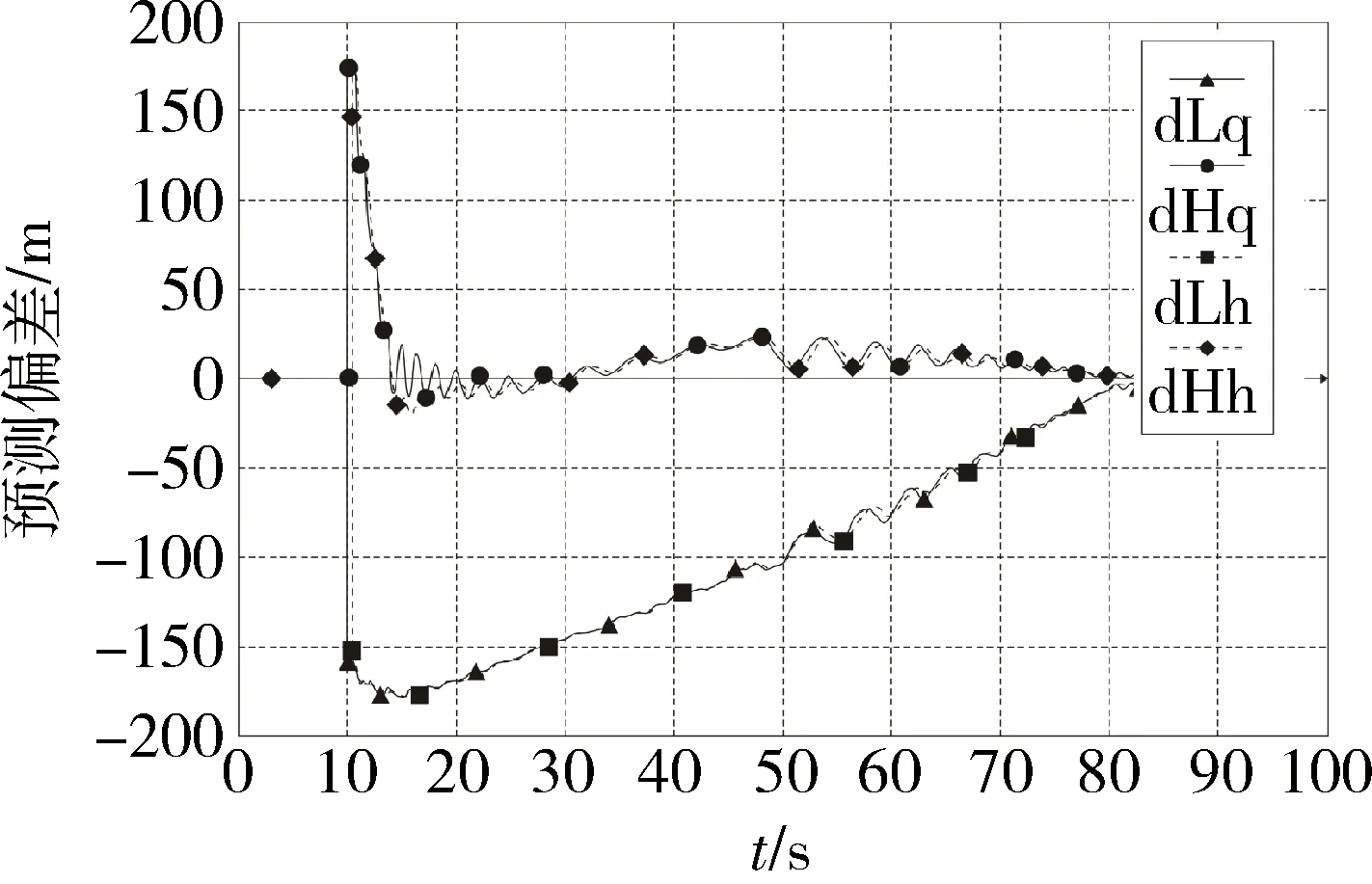
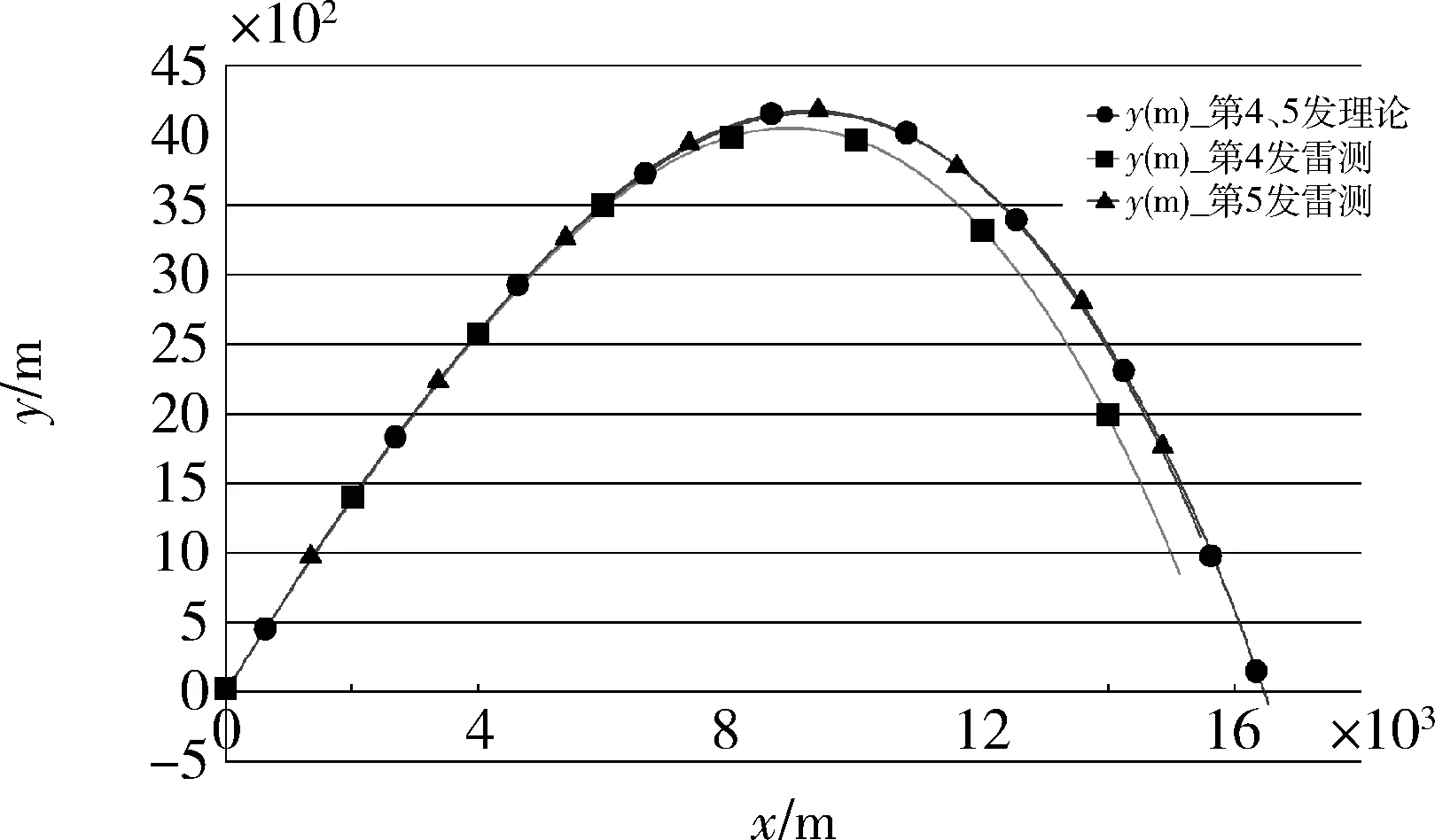
根据GPS导航数据中的位置精度因子PDOP和收星数来判断GPS导航数据的可用性,当0 如果GPS导航数据可用,则完成解算预测落点偏差及滤波处理,并进行如下操作: (7) 如果GPS导航数据不可用,则将舵偏回零且进行如下操作: GPS_valid=0 (8) 式中:ΔL和ΔH为实际控制用的预测落点纵向和横向偏差;GPS_valid为GPS导航数据可用标志,1表示可用,0表示不可用。 2.2.2 摄动制导指令的生成 摄动制导的以预测落点为控制量,纵向位移x为基准的落点预测偏差算法如下: (9) (10) 2.2.3 制导指令滤波处理 纵向制导指令的滤波公式为: (11) (12) (13) HΔL=(1-βΔL)2 (14) 摄动制导段: (15) 横向制导指令的滤波公式为: (16) (17) (18) HΔH=(1-βΔH)2 (19) 摄动制导段: (20) 在对滤波器赋初值和对预测落点偏差进行滤波处理前,需要根据武器系统的弹道特性判断数据有效性;如果数据无效,则不对当前数据进行滤波处理,并设置GPS_valid=0。 a.连续5帧GPS导航数据可用,计算出制导量; b.GPS导航数据可用性从不可用状态变为可用状态,且连续5帧GPS导航数据可用,计算出制导量。 2.2.4 制导滚转角指令及驱动使能指令计算 每个导航周期内(0.1s),制导滚转角指令及驱动使能按如下公式计算更新: (21) dA=Interp1(tArr,dAArr,t) (22) dB=Interp1(tArr,dBArr,t) (23) (24) (25) 否则,进行角度区间映射, (26) γc=Proj(t,Φ′,sw1,sw2,sw3,sw4) (27) 式中:A为综合修正偏差量;dA为修正阈值;dB为最优方位修正阈值;enble为驱动使能指令;γc为滚转角指令;Interp1为插值函数;Proj为角度映射函数。 为验证控制系统方案可行性,进行了控制系统的数字仿真[13],包括修正能力仿真和制导精度仿真。在数字仿真的基础上进行了实弹测试,共发射5发试验弹。 为验证PGK组件的修正能力能否覆盖无控弹的散布范围,在155mm榴弹平台和152mm榴弹平台上进行了修正能力仿真。通过调研和仿真分析得到的无控弹的散布范围如表1所示。PGK组件在不同平台上的修正能力仿真结果如表2和3所示。 表1 无控弹修正能力对比 表2 155mm榴弹平台修正能力仿真结果 表3 152mm榴弹平台修正能力仿真结果 在成熟型号单通道滚转控制技术的基础上,建立七自由度弹道模型,设计转角“刹车”控制的制导控制算法。在给定初始干扰的条件下进行了制导精度仿真,制导仿真结果如图6~9所示。 图6 预估偏差制导曲线(纵向正偏差,横向正偏差) 图7 预估偏差制导曲线(纵向正偏差,横向负偏差) 图8 预估偏差制导曲线(纵向负偏差,横向负偏差) 图9 预估偏差制导曲线(纵向负偏差,横向正偏差) 2017年9月16号,试验队赴051基地阿拉善试验靶场组织开展了PGK修正能力验证飞行试验。本次试验共发射5发试验弹,用于验证常温下的PGK组件修正能力。5发试验弹的飞行试验主要弹道参数如表4所示。 表4 飞行试验主要弹道参数 2017年9月20日上午,采用36°射角发射了3-9#试验弹,试验弹全程飞行稳定,雷测跟踪正常,PGK组件在50.3s正常开舱,开舱点高度1535m,距离发射点15770m。回收数据显示,PGK组件转速异常,未能正常控制,GPS导航模块工作异常,全程未定位。理论弹道根据出炮口速度为660m/s,阻力修正系数90%等参数进行拟合。3-9#试验弹与理论弹道对比如图10所示。 图10 3-9#与理论弹道对比 经过对硬件故障的改进处理后,2017年9月26日下午,采用36°射角发射了3-9#、4-4#和4-9#试验弹,4-4#试验弹全程飞行稳定,雷测跟踪正常。4-9#试验弹全程飞行到30s后姿态异常,出现失速,PGK组件在52s正常开舱,开舱点高度1862m,距离发射点13987m。回收数据显示,供电电流正常,地磁数据正常,舵机控制正常,GPS通信正常,控制运算正常。4-4#、4-9#试验弹弹道与理论弹道对比如图11所示。 图11 4-4#、4-9#与理想弹道对比 从图中可以看到,前3发试验弹弹道与理想弹道有一定差别,无法达到预期的制导精度。针对前两次试验中制导效果较差的问题,对修正段控制进行了如图12所示的优化[14]。根据瞬时运动状态参数和理想弹道参数的对比,计算出基于比例反馈模型的摄动制导导引系数,并实时对制导指令进行更新。 图12 优化修正段控制流程图 进行改进处理后,2017年9月27日下午,采用36°射角发射了4-10#和3-5#试验弹,4-10#试验弹全程飞行稳定,雷测跟踪正常,PGK组件在52s正常开舱,开舱点高度844m,距离发射点15132m。3-5#试验弹全程飞行稳定,雷测跟踪正常,PGK组件在52s正常开舱,开舱点高度1112m,距离发射点15469m。回收数据显示,供电电流正常,地磁数据正常,舵机控制正常,GPS通信正常,控制运算正常。4-10#、3-5#试验弹弹道与理论弹道对比如图13所示。 图13 4-10#、3-5#与理想弹道对比 可以看出3-5#试验弹与理论弹道高度拟合,达到了预期的制导精度。4-10#试验弹略偏近,实测速度略偏低,下面对4-10#进行拟合分析。 将4-10#试验弹的阻力修正系数取值从90%更改为94%,初速由666.4m/s更改为661.4m/s。拟合计算弹道曲线对比如图14所示。 图14 4-10#弹道拟合计算 由图14可知,拟合计算弹道与雷测弹道吻合较好。以上结论说明,不同试验弹个体之间阻力特性存在差异。在合适的阻力修正系数情况下,4-10#与3-5#试验弹均有较好的制导表现。 根据所使用的PGK的控制原理和系统结构,提出了一种高精度的一体化PGK控制算法。该算法可实现判断GPS信号可用性,计算导弹和目标的相对运动关系并生成滤波制导指令和制导滚转角指令,最终通过控制鸭翼面实现控制功能。数字仿真结果验证了算法在不同平台可以达到一定的修正精度,达到了预期的修正能力要求,且具有一定的抗干扰能力。实弹试验中修复了硬件异常并对修正段控制算法进行了优化,优化后的试验弹制导精度上升,试验弹弹道与理论弹道高度吻合。在后续研究中,可以尝试将摄动制导方法用更复杂,具有更高精度和灵活性的比例导引方法替代,进一步提升一体化PGK的制导能力。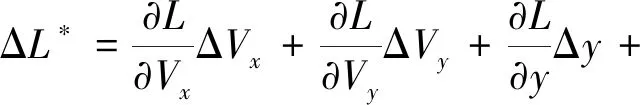



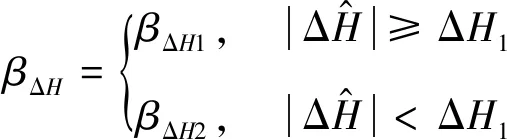

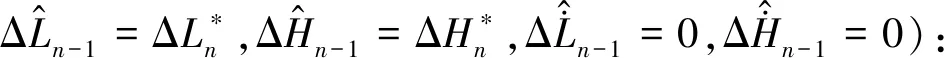

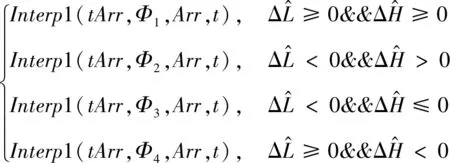
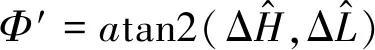
3PGK控制系统仿真和实弹测试
3.1 修正能力仿真



3.2 制导精度仿真


3.3 实弹试验





4 结论
