基于小波神经网络的燃气轮机故障诊断研究

刘隆波，黄金娥，沈君贤

1.92942部队， 北京100161 2.哈尔滨工程大学 航天与建筑工程学院 黑龙江 哈尔滨 150001

随着现代制造技术的提升，对燃气轮机的性能和工作条件要求越来越高，同时也出现了更多的机组故障，因此对汽轮机运的故障诊断提出了更高的要求。燃气轮机故障诊断可以根据机组发生故障时的振动信号找出故障的特征信息，并利用它进行故障预警和排除，从而指导维修任务[1]。关于故障诊断，很多专家学者对此做了大量的研究。西工大宋晓萍和廖明夫[2]使用快速傅里叶变换分离法和盲源分离法分离双转子飞机发动机的振动信号，并利用FastICA算法对不同频率的振动信号进行分离。海军航空工程学院王晓钢[3]提出了贝叶斯数值理论应用于航空发动机汽轮机故障诊断,通过建立燃气轮机数值诊断贝叶斯理论模型,计算出系统的故障状态的根源失效概率,通过使用极限状态识别规则,确定工作状态。本文以舰船汽轮机为研究对象，通过功率谱密度故障筛选出疑似故障，用小波分析提取故障特征向量，最后输入训练好的神经网络进行识别，实现了汽轮机故障的综合故障诊断，具有一定的工程意义和应用价值。

1 信号筛选

由于大多数旋转机械在故障时刻，对于不同频率能量的变化比较敏感。因此，本文选择功率谱密度进行信号筛选。首先，功率谱密度是将时间域的振动描述转化为频率域的振动描述，即信号在时间域的总功率等于在频率域的总功率，可以得到随机过程的功率谱密度[4～5]。其次，通过加窗来减少非整数周期给傅里叶变换带来的误差，Hanning窗具有较好的频率分辨率，还可减少频谱泄露。经过处理的信号得到加速度功率谱密度，它反映信号不同的频率段的能量分布[6]。

在工程试验中数据采集是连续长时间的，对每个时间段的信号都进行细化的分析将会大大增加工作量。由于特定故障发生存在固定频率，大多数是在基频的倍数出现峰值。因此，可以对功率谱密度图进行典型频率段划分。只需监测典型频率段内振幅有效值的变化就能在大量数据中筛选故障段。在试验现场，对固定测点监测易发故障的典型频率段，就能快速发现疑似故障，细化分析后进行及时检修。对于旋转机械，根据基频选择划分区间如下：

ω=[kX-5,kX+5]

k=1,2,3,4

(1)

式中：X为汽轮机的基频。

选择转子不平衡、齿轮缺陷、紧固件松动3种汽轮机常见的故障作为诊断研究的基础，通过将正常状态信号与转子不平衡、齿轮缺陷、紧固件松动故障时功率谱密度图进行比较。

1)转子不平衡

传感器布置在转子支承座处，通过功率谱密度(power spectral density,PSD)故障筛选出一个基频的突变信号。转子的不平衡故障往往对应着基频峰值的出现。由图1可以清楚地看到基频峰值信号从0.39突变到3.08，突变将近10倍。此时，发生了转子不平衡的故障。

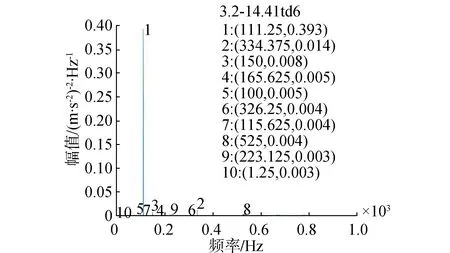
(a)正常状态

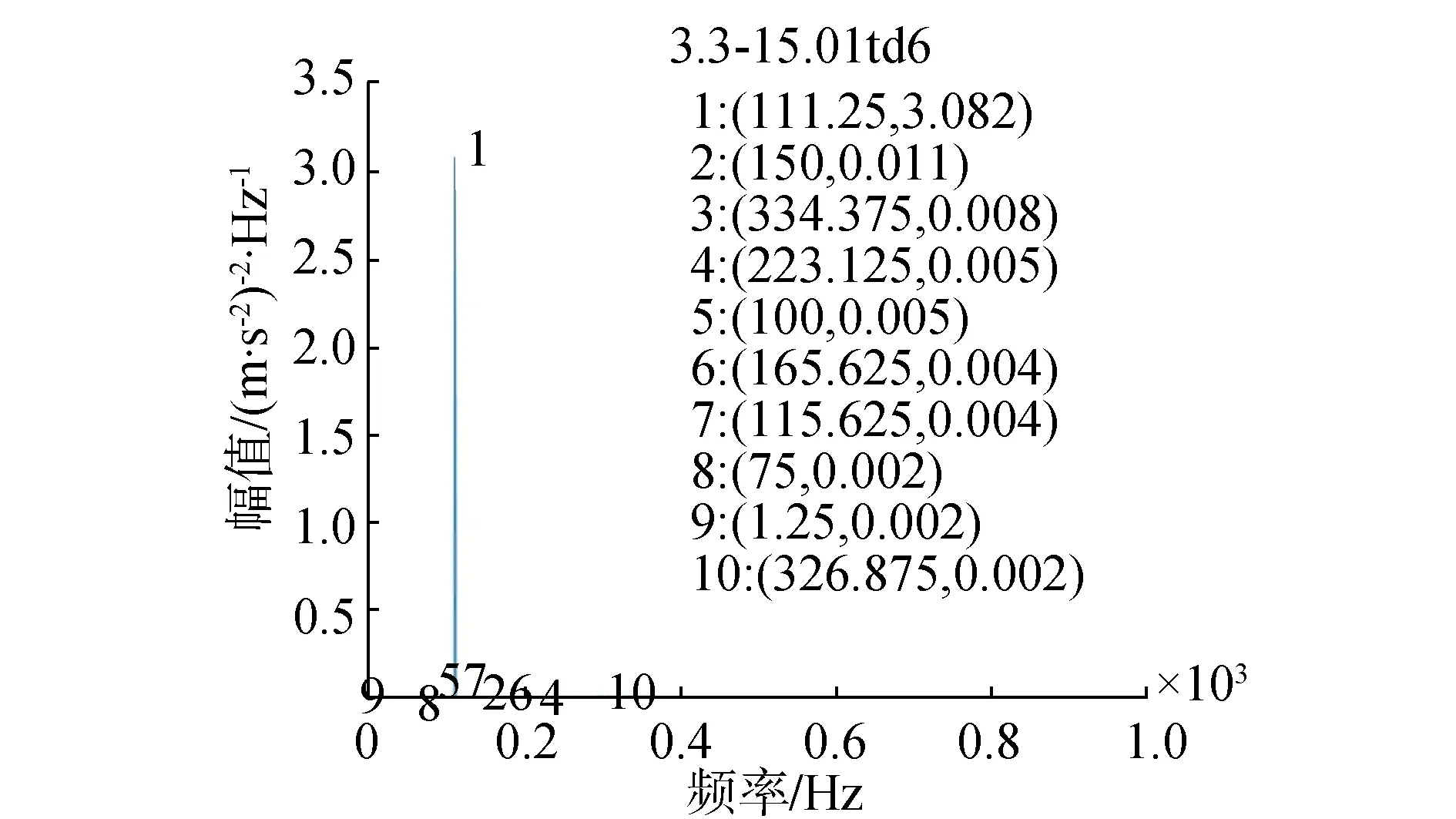
(b)故障状态图1 转子不平衡频谱图

2)齿轮缺陷及传力不均匀

传感器布置在齿轮箱处，通PSD故障筛选出一个基频的突变信号。齿轮缺陷及传力不均匀故障往往对应着基频与齿数乘积频率峰值的出现。由图2可以清楚地看到在齿轮箱处传感器测量信号的基频峰值信号从2.13突变到12.40，突变将近6倍，此时，发生了齿轮缺陷及传力不均匀的故障。

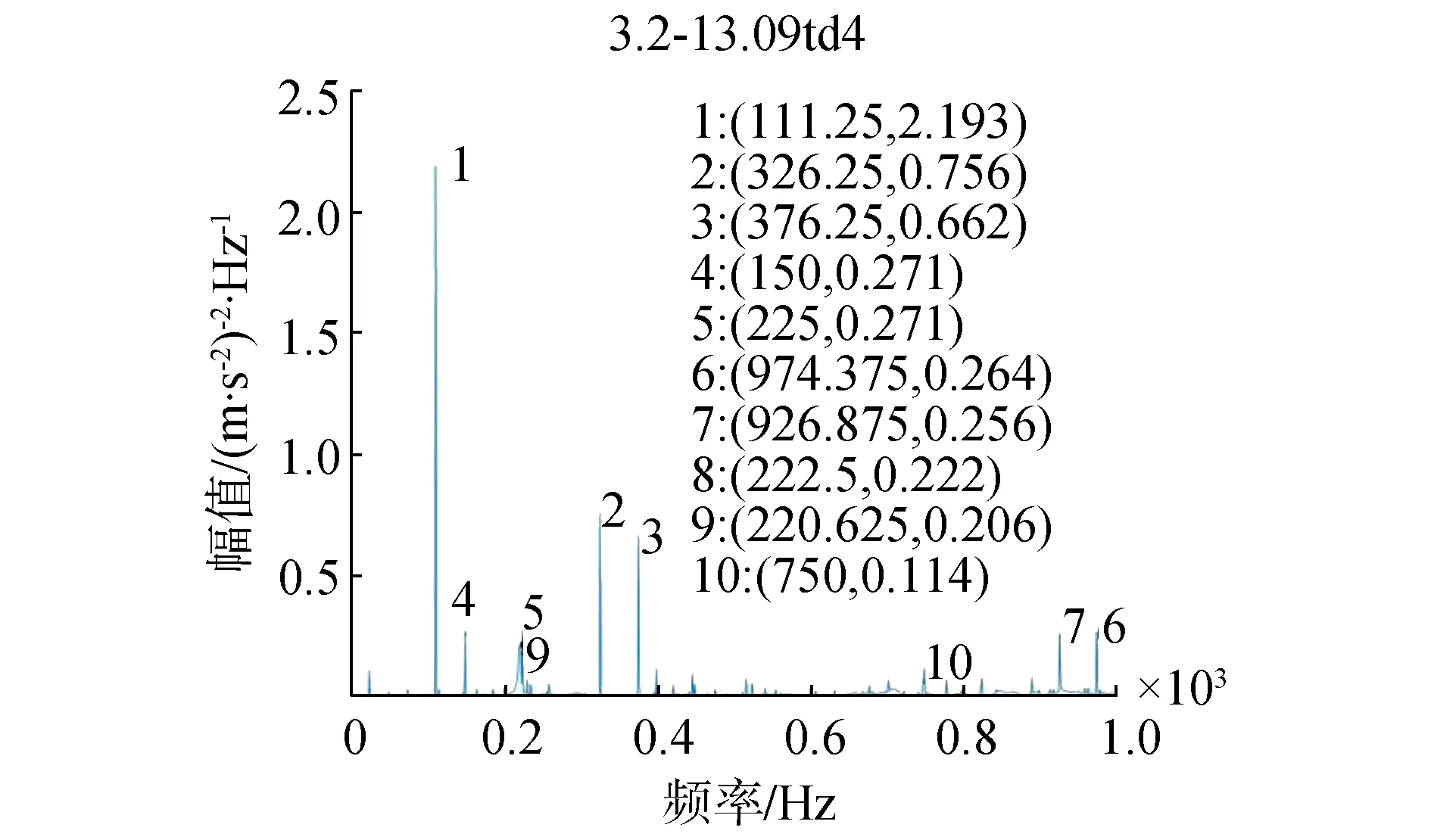
(a)正常状态

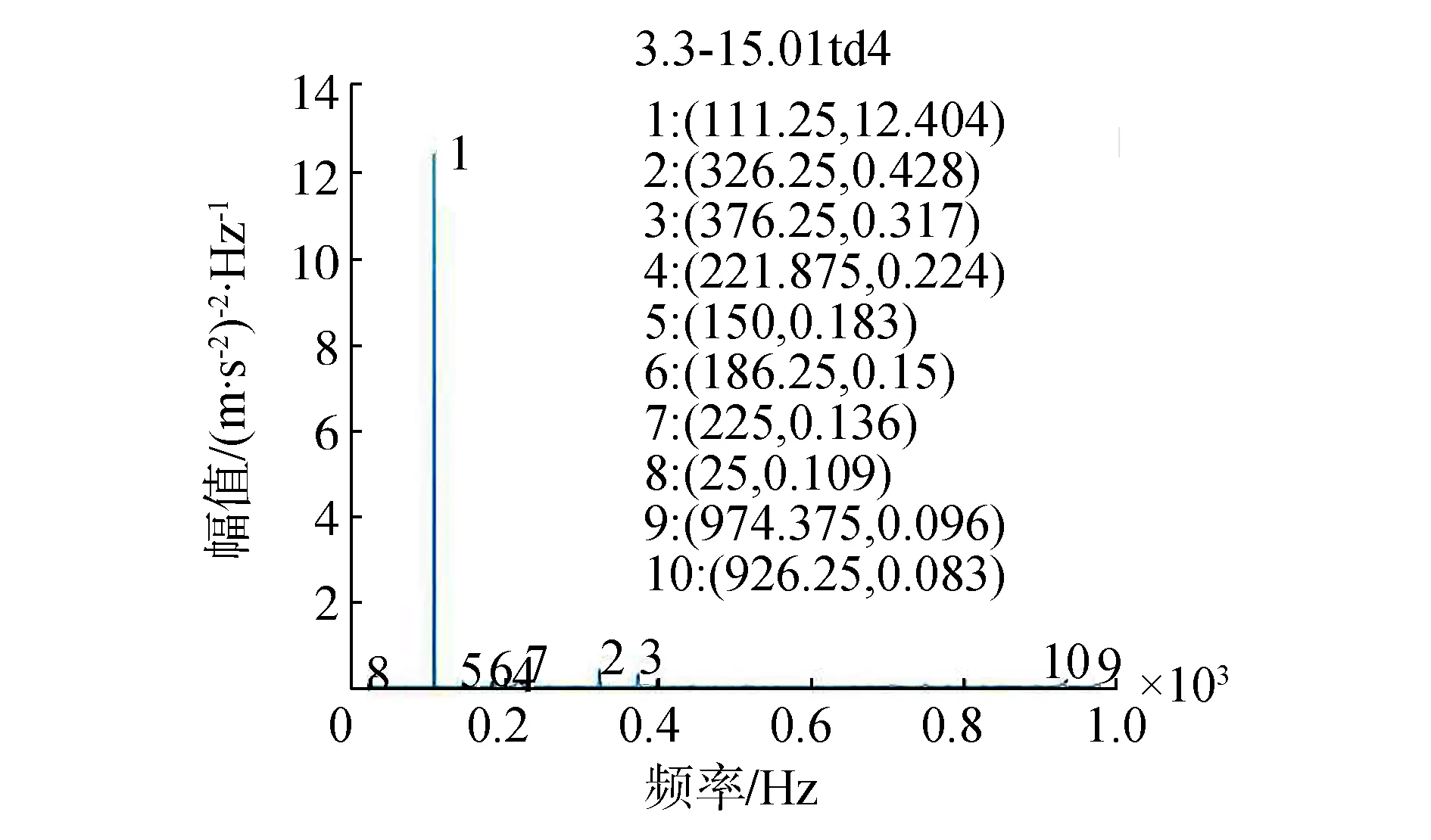
(b)故障状态图2 齿轮缺陷及传力不均匀频谱

3)紧固件松动

传感器布置在轴承处，通过PSD故障筛选出3倍基频的一个峰值信号。根据经验，可以认为：如果3X峰值最大，是轴与轴承间的松动；如果是4X有峰值，是由于轴承本身是松动的。此时3X频率(333.75 Hz)处峰值的出现，由图3可以清楚地看到在轴承处传感器测量的信号由基频峰值信号向3倍基频峰值的变化，此时对应发生了轴与轴承间松动的故障。

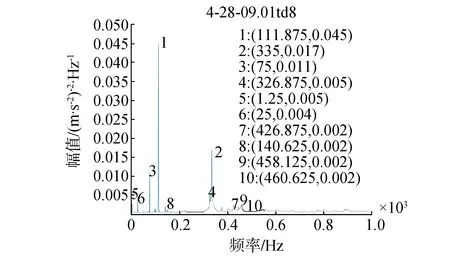
(a)正常状态

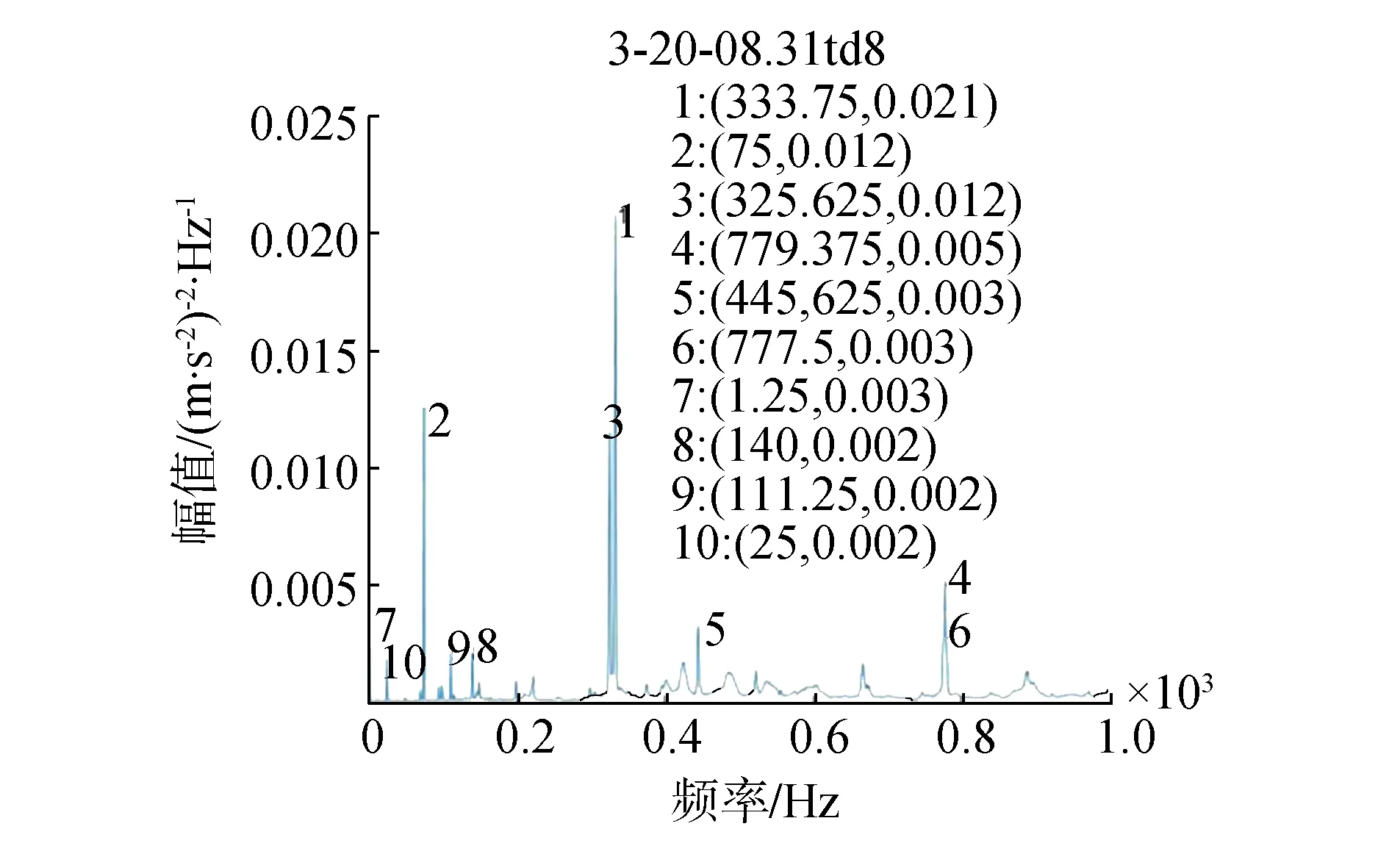
(b)故障状态图3 紧固件松动

2 基于小波变换的故障特征提取

2.1 小波变换

在信号处理中使用最广泛的是傅里叶变换，但是它存在一种缺乏时域信息的缺陷。小波变换的概念最早是由法国工程师j.m.orlet于1974年提出的，它是时间和频域的局部转换[7]，由于结合了时域和频域的优势，它可以对故障信号进行细化、放大。小波变换的这些特点能够从故障信号中提取有效信息，通过同时具有时域频域双表达特性，解决了大量傅里叶变换难以处理的问题。这对于提取瞬时变化的振动信号特征是十分必要的。

小波基库由许多小波基组成。不同的小波基能够反映信号不同的特征。因此，根据信号特征的不同，最好能够选择一个最优的小波基来表达信号特征。另外，小波基函数的选取直接决定了信号特征提取的效果[8]，进而影响故障诊断。然而，在小波分析中，并没有一套选择小波基的准则。通常情况，根据信号的特征不同来进行小波基的选取。根据文献，陈泽鑫[9]提出了对于冲击信号，选择最优小波基来提取故障特征信息的方法。本文通过对比相似性系数，选取Sym8作为最优小波基函数。Sym8函数形状与信号波形相近，这样能够抑制不同形状信号，放大相近部分信号特征，从而达到提取信号故障特征目的。

2.2 故障特征提取

振动信号经过小波变换后能够分解到不同频段上并且保留时域信号特征。不同频段对应着不同故障的特征频率，如果能够准确提取各个频带分量的信号特征作为信号特征向量就能有效地对燃气轮机故障进行诊断。在此基础上，选择5种统计特征参数就可以更精确地描述装备不同角度的状态特征。这些统计参数分别为方根幅值、有效值、峰值指标、峭度、裕度指标。在经过小波分解后的振动信号，各个频带的信号相当独立。故障信号集中在固定的频率段，也就是固定的层数。通常的分析方法是提取每个频带的能量(信号的均方根值)作为故障特征向量，但是这种方法对于多故障有一定局限。有时候不同故障的能量信息是相同的，光从能量角度判断过于单一，缺乏稳定性。本文选择了5种有量纲与无量纲的参数进行多角度提取故障信号特征。表1给出信号筛选出的转子不平衡故障的特征提取数据。

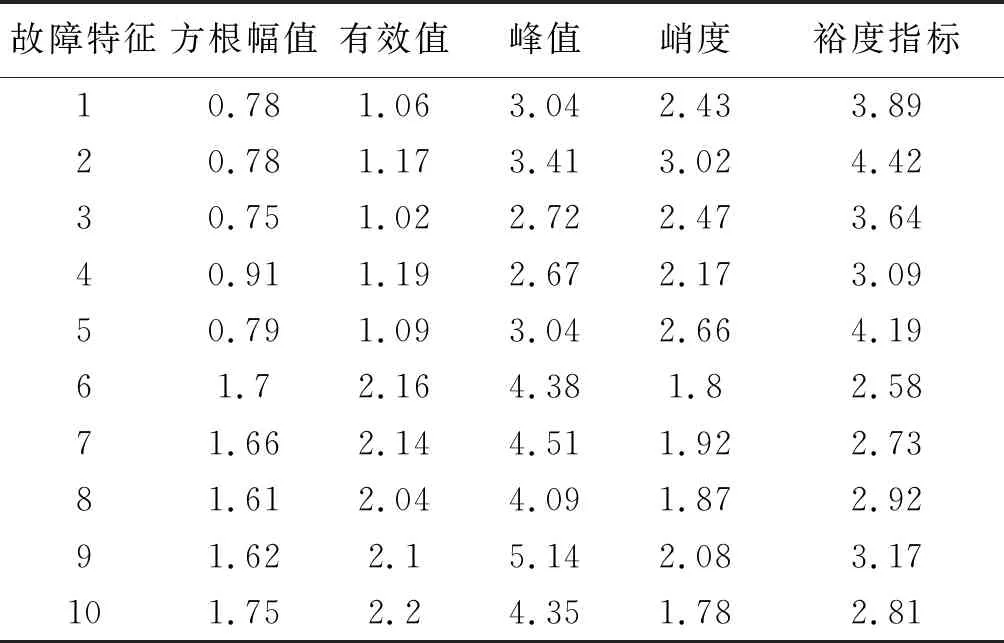
表1 故障统计参数提取表

3 基于BP神经网络的故障识别

采用传统的故障分类识别方法，故障诊断的稳定性与可靠性得不到保证。本文提出人工神经网络故障识别分类方法，选择具备误差反向传播的学习模式BP神经网络。BP神经网络通常包含多个隐含层，其学习训练分为前向计算和误差的反向传播计算。在正向传播过程中，输入信号方差归一化后从输入层经隐层逐层处理传向输出层，每一层神经元的状态仅影响下一层的神经元状态。如果输出值与期望不符，神经网络会根据误差从后向前逐层进行修正各层神经元状态权值，使误差信号达到最小[10～12]。具体过程如下：

1)初始化：确定网络的输入层、隐含层和输出层的节点个数。随机初始化BP神经网络权值和神经元阈值。

2)前向传播：把输入值作方差归一化处理，按照公式计算隐含层神经元和输出层的输入与输出。

3)后前传播：比较输出值与期望值。若存在误差，由误差反向传播更新权值和阈值，直至满足最终条件。

4)用训练好的BP神经网络对疑似故障样本进行识别。

4 综合故障诊断实例

本文提出基于小波变换和BP神经网络的故障诊断方法，其算法流程如图4所示。

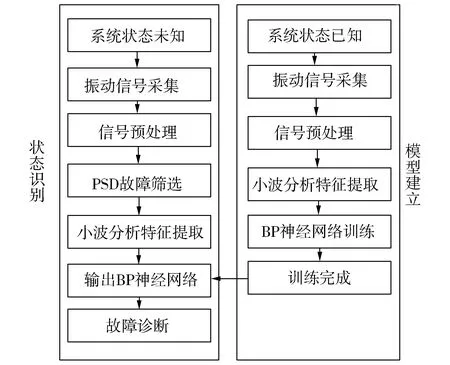
图4 算法流程

图4中的具体步骤为：

1)信号筛选：先挑选同一工况内的振动信号，对信号进行FFT变换，加Hanning窗得到信号的功率谱密度。根据式(1)划分功率谱密度的典型频率段，计算这些频率段中幅值的有效值，观察有效值的突变判断该信号中是否有疑似故障段。

2)小波变换：使用小波对疑似故障段信号进行分解，获取疑似故障频率段的信号分量。计算信号分量的方根幅值、有效值、峰值、峭度、裕度指标，并构成最终的特征向量。

3)BP神经网络的故障诊断：先将同一工况已知的正常与故障信号特征向量组成矩阵，方差归一化后作为标准特征的训练样本输入BP神经网络。经过训练后的BP神经网络，输入试验中出现的疑似故障段的特征向量，即能进行故障识别。

对4种已知状态正常、转子不平衡、齿轮缺陷、紧固件松动的数据用小波分析提取特征向量，分别选取5组特征向量训练神经网络。最大训练次数为500次。设学习率与动量因子分别为0.1和0.3。目标误差设置为0.01。由于输入的特征参数依然选取5个，确定了神经网络隐含层节点数为5，输出值为1个三维向量。表3给出了神经网络输出对应的不同状态。

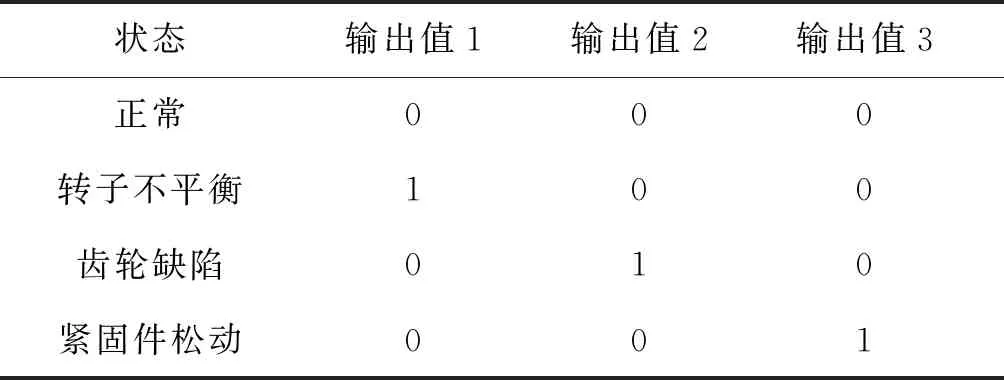
表2 不同状态对应的输出表

经过300次迭代训练，神经网络训练完毕。为了证明方法的有效性，对上述训练好的神经网络进行测试。测试数据运行相同的特征提取方法，经方差归一化后输入神经网络识别。归一化后得到的测试样本数据如表3所示。

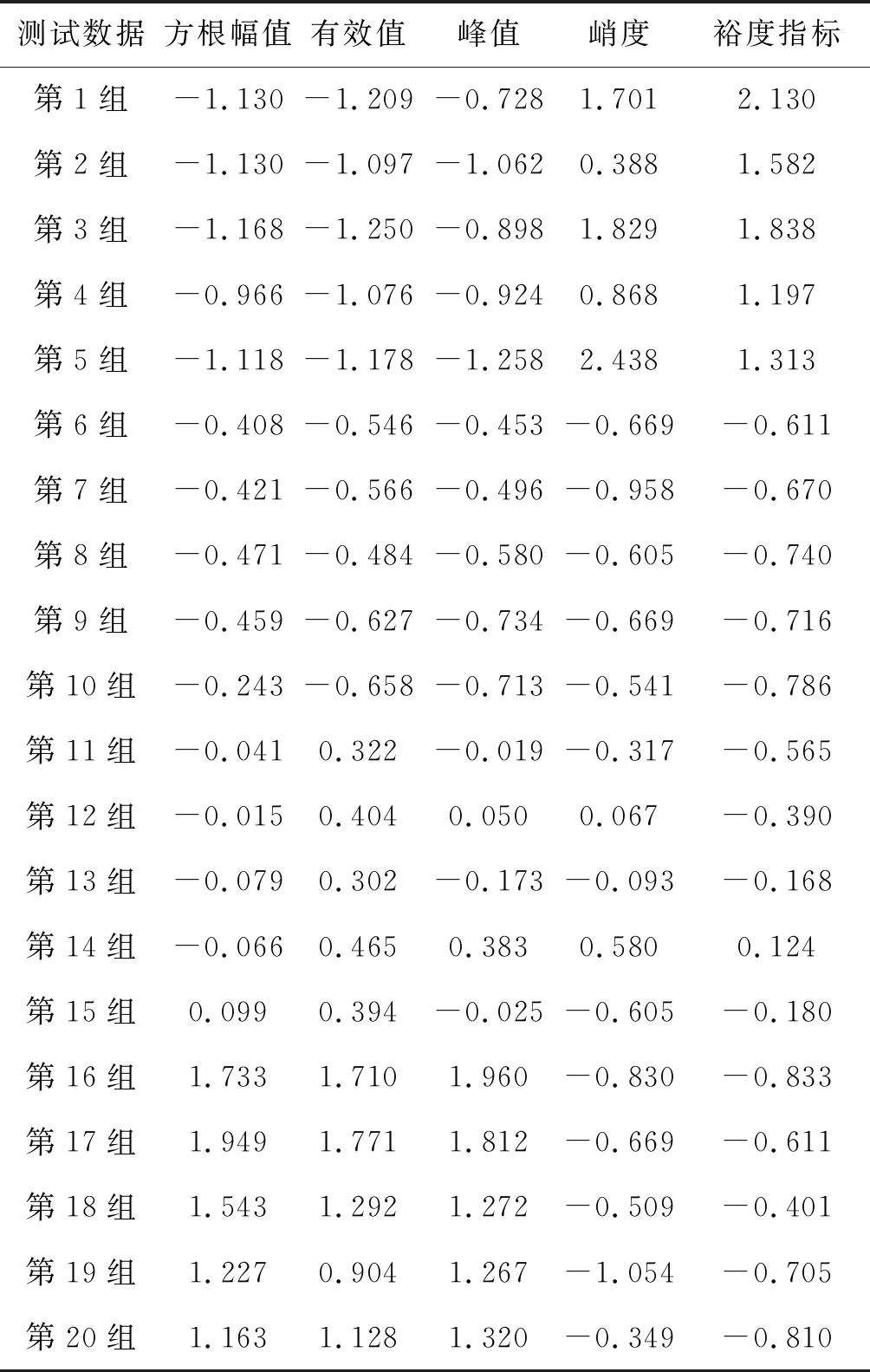
表3 归一化后得到的测试样本数据表

表4为经过测试后的输出值。表中第1组数据为[-0.212，0.192，-0.181]，这3个数据对于0和1，更加接近0。因此故障输出值为[0,0,0]。由故障输出代码表可以判断此时发动机为正常运行状态。一般也可以根据小于0.5或大于0.5判断输出值是接近0还是1。如第11组数据[0.191,0.927,0.305]，根据0.5这一阈值判断得到的故障输出值为[0,1,0]。由故障输出代码表可以判定此时发动机存在齿轮缺陷故障。

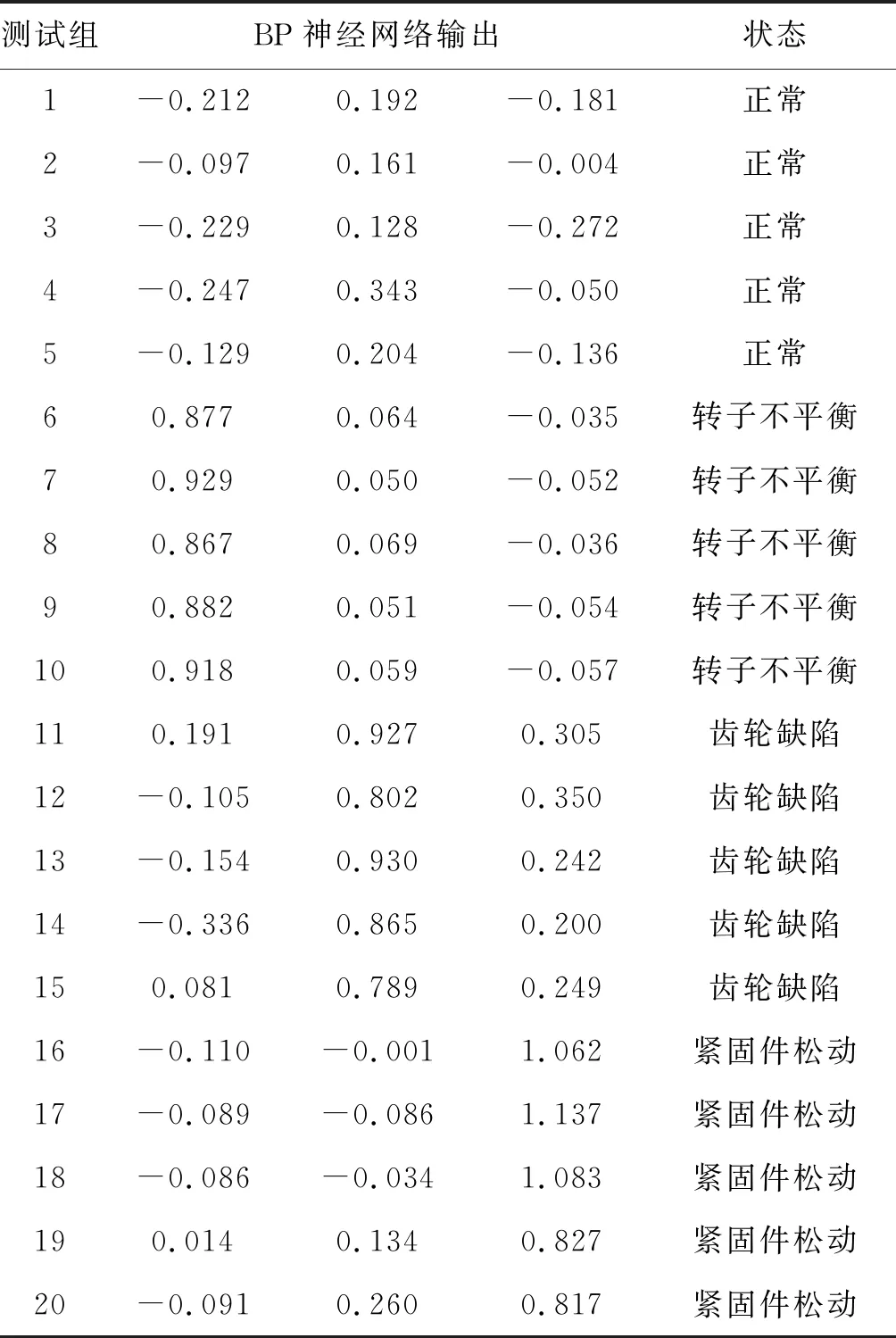
表4 BP神经网络输出与状态判断表

后续通过1000组数据的测试，综合故障诊断率能够达到97.5%。说明小波与神经网络结合的故障诊断方法对故障诊断有着较高的识别准确率。

5 结论

本文通过研究基于小波分析与BP神经网络相结合的故障诊断方法，以舰船燃气轮机试验数据为应用对象，验证了该方法用于舰船燃气轮机等旋转机械故障诊断的可行性和工程适用性。根据结果分析，可得出以下结论：1)本文选取的试验振动数据，通过PSD进行故障筛选的方法能快速判别机组运行是否出现故障状态；2)以变换后信号的特征参量作为神经网络的输入，实现了对3种典型故障状态的识别，形成了具有较高准确率的燃气轮机故障诊断方法。