大型水轮发电机组发电机转子测圆方法浅析
2019-09-23张海宏肖金磊
张海宏,肖金磊
(中国长江电力股份有限公司检修厂,湖北 宜昌443002)
1 引言
机组在长期运行过程中,受到电磁力、机械力等因素的影响,转子圆度可能会发生变化,转子磁极不圆是导致大型水轮发电机组定子与转子间空气间隙不均匀的主要因素之一,转子圆度直接影响转子的机械性能和电磁性能,进而影响机组的安全稳定运行。转子测圆的目的在于检查转子圆度是否在标准范围之内。
利用旋转测圆架对发电机转子进行测圆,首先要对测圆架的中心、水平进行安装和调整,测圆架的水平与中心不仅精度要求高,且水平调节和中心调节相互影响、互相干涉,致使转子测圆工作效率不高。本文通过对转子测圆方法的误差分析与计算,基于excel计算对转子测圆过程中产生的误差进行控制,并通过转子测圆补偿测量法,提高测圆数据的有效性和准确性。
2 转子旋转测圆架
转子旋转测圆架由底座、回装中心体、拉紧装置以及配重臂、测量臂等部件组成。如图1所示,通过调整配重臂使测圆架受力均匀,减少了测圆架固定部分和旋转部分的受力不均,进而减少误差。用百分表进行测量,精度高,便于灵活控制。
目前广泛使用的转子旋转测圆架为中空测圆架,即测圆架有求心设计,目的是使测圆架的中心可以进行调整,使测圆架中心与转子同心。
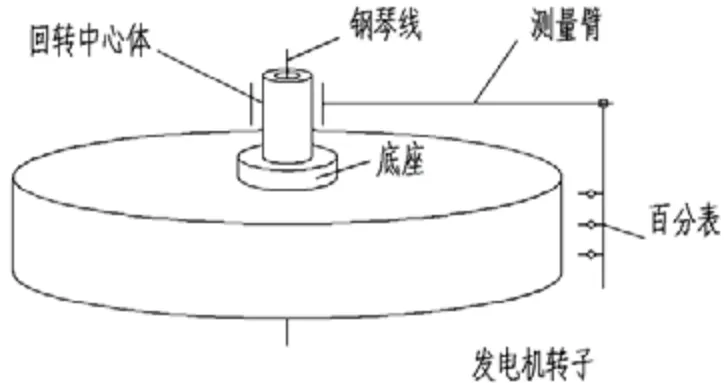
图1 转子旋转测圆架示意图
3 测圆方法简介及分析
3.1 测圆方法简介
将测圆架置于转子上方,在测圆架上、中、下三个位置上架设百分表,表针垂直于磁极表面;在测圆架中心体内架设钢琴线,反复调整测圆架,使测圆架与转子中心同轴;使用合像水平仪测量测圆架水平,并反复调整测圆架拉紧装置直到使测圆架与转子平行。试转一周,检验测圆架是否灵活以及有无憋劲现象以及百分表回零情况,再旋转测圆架进行转子测圆并记录数据。
对于中心不能使用钢琴线调整的测圆架,测圆架水平合格后,先旋转测圆架一圈进行测量并记录数据。通过数据分析,选取垂直对称4个方向偏差最大值为基准,调整其中心为0,再进行测圆,得出的数据也可反映转子圆度。由于其测量精度不高,目前使用较少。
3.2 误差分析
不考虑测圆架强度和本身缺陷,即认为测圆架旋转时测量臂所有测点轨迹为圆,圆中心线为测圆架中心体的中心线,误差来源主要有测圆架中心、水平调整带来的误差以及百分表在磁极表面测点位置不一致产生的误差。
(1)测圆架中心调整误差。如图2所示,即测圆架实际中心与转子中心未重合,存在一定的偏差值。测圆架安装中心偏差直接影响测圆架测量臂与磁极表面测点的距离,影响测圆数据。假设测圆架实际中心与理想中心在某方向上偏差0.01 mm,则测圆数据在该方向上偏差可达到0.02 mm。
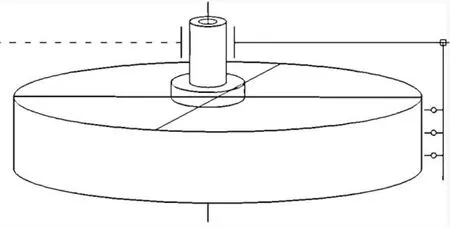
图2 测圆架中心偏差
(2)测圆架水平调整误差。测圆架与转子不平行,测圆架实际水平值存在一定偏差,致使测量臂与磁极形成一定角度且垂直距离发生改变,影响测圆数据。测圆架水平不合格,相当于测圆架从水平位置旋转了一个角度,导致测量臂测点位置与转子磁极的水平距离和测量角度均发生变化,进而导致测量偏差。

图3 测圆架水平偏差
设测圆架水平调整偏差为Δz mm/m,不考虑其他因素。设转子直径为Φ1,转子高度为h1,则测点与测圆架水平偏差中心夹角为,测圆架旋转平面与转子中心的偏差角为则偏差后的连线角为
因为水平偏差,测圆架支臂端点在水平方向上的位移为:
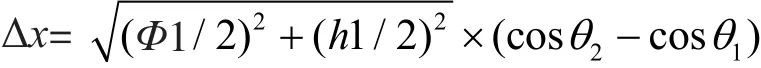
测量臂上的百分表测量的是测量臂端点与磁极表面的倾斜距离,则测量偏差为
由于测圆架水平偏差一般较小,一般都控制在0.05 mm/m以内,可以近似认为测圆架的圆度测量偏差Δa就是测量臂端点在水平方向上的位移,即Δs=Δa。
以葛洲坝电站机组发电机转子参数来进行理论计算分析为例,具体参数如下:
转子直径为14960 mm,转子高度为1850 mm,假设测圆架水平调整偏差为0.01 mm/m。
通过上述公式计算,不考虑其他因素影响的前提下,可以得出测量值偏差基本与测圆架水平偏差成正比关系,水平偏差每偏差0.01 mm/m,对应圆度测量值偏差0.01 mm。
(3)百分表测点位置偏离磁极中心产生的误差。如图4所示。不考虑磁极本身因素的影响,同样以葛洲坝电站发电机转子参数进行理论计算分析为例。转子半径为7480 mm,转子磁极冲片外圆弧半径为1320 mm,设测点位置偏离磁极中心1 mm。由于偏离距离远小于转子半径,可简化计算得到测量偏差为=0.00038 mm,从而得出,在不考虑其他因素影响的前提下,百分表测点位置偏离磁极中心误差达到5 mm时,圆度测量偏差达到0.01 mm。
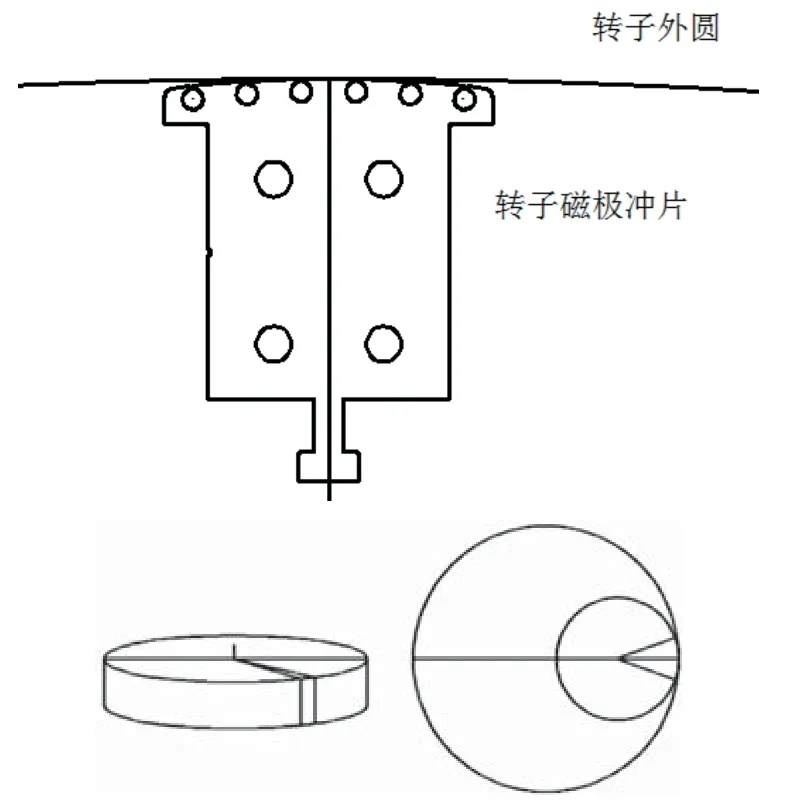
图4 百分表测点偏差示意图
4 转子测圆的修正测量法
补偿测量法主要对测圆方法中测圆架的安装调整简化,并在得到数据后进行后期处理,以达到提高效率的目的。测圆架调整的主要难度在于测圆架水平和中心调整的相互干扰,因此将其调整过程简化为只进行水平调整,测圆架的中心偏差作为最后计算的修正量。
调整测圆架水平合格,调整测圆架钢琴线位于测圆架旋转中心体中心。测量钢丝线与转子中心体垂直四个方向上的距离,得到测圆架相对转子的中心偏差。旋转测圆架一圈进行测量,记录数据。通过excel表格对数据进行修正计算,从而得到转子圆度数据。
本测量法的误差主要来源是测圆架中心调整由原来调整到(0,0)到现在记录一个具体值(x,y)。
5 转子测圆方法优化改进及分析
测圆架水平合格的前提下,测圆架的中心偏差除了通过使用内径千分尺测得外,也可通过在旋转中心体上安装一个可拆卸类似于测量臂的支架,在支架上架设百分表,旋转测量其到转子中心体内镗口的距离,并记录相应磁极位置处转百分表的读数。对所有数据组进行修正计算,从而得到转子圆度数据。
现假设转子测圆架水平调整完成之后,假设测圆架中心测得为(Δsx,0),磁极数为n,转子半径为S。
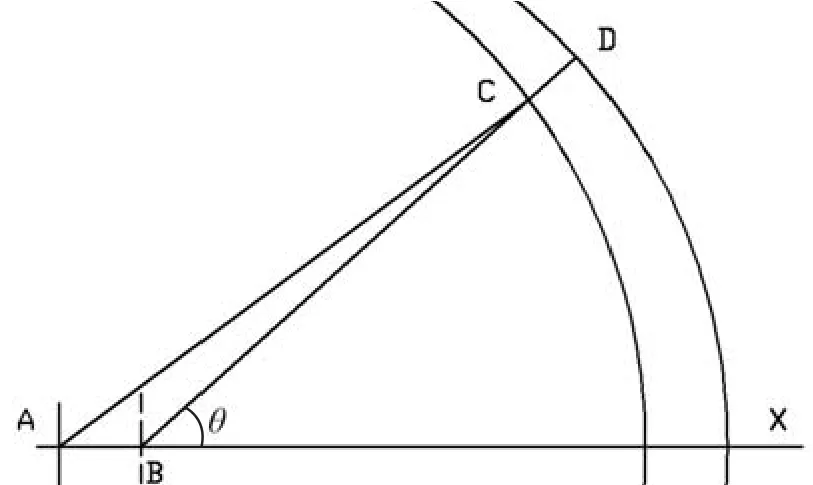
图5
对于第m号磁极上的测量点D,则θ=∠DBX=,以 A(0,0),则 B(Δx,0),C(Scosθ,Ssinθ),
以葛洲坝电站发电机转子为例,依次计算96个磁极,在0.01 mm中心偏差下的补偿量分布如图6。

图6
本测量方法对转子磁极和转子中心体内镗口同时进行测圆。在测圆架中心与理论中心偏差为(0.01 mm,0)的情况下,可以计算出对转子中心体测圆数据,见图7。
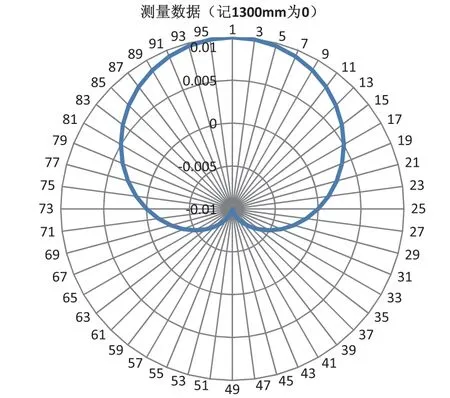
图7
比较数据发现,对转子中心体测圆的数据与测圆中心调整后数据基本一致,经过excel计算,两者的差距最大值小于10-7mm。因此,在这种测量方法中,可以直接将每个磁极测圆数据和转子中心体内镗口的百分表数据相减,可得到最终测圆数据。省去测圆架中心的反复调整,而理论上误差仅为0.01 mm。
6 结语
对比传统方法,优化后的转子测圆方法,简化了工艺流程,省去了中心调整过程,计算简洁直观,提高了转子测圆的效率和转子测圆数据的准确性。
