基于变尺度搜索算法的混沌MIMIC算法

赵晋彬,夏桂梅

(太原科技大学 应用科学学院,山西 太原 030024)

分布估计算法(EDAs)的基本思想是利用变量间的概率分布来表示变量之间的相关关系,并经过迭代进化,迫近问题的最优值,降低了对问题先验知识的要求,是一个很好的连锁学习算法[1]。混沌算法是一种收敛较快的优化算法,具有遍历性和随机性。这样的特征,可用于局部优化,但它有初值选择的敏感性,因此传统的混沌算法对目标难以瞄准。变尺度搜索可以缩小搜索区间,使得算法更容易找到最优解[2]。在MIMIC算法和混沌搜索算法结合的前提下,引入变尺度搜索,优化搜索空间,提出基于变尺度搜索算法的混沌MIMIC算法(MSCS-MIMIC)。

1 MSCS-MIMIC

1.1 MIMIC算法

MIMIC算法是一个在双变量相关、链式结构依赖假设基础上提出的分布估计算法,其概率图模型如图1所示[3]。

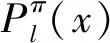
图1 MIMIC的概率图模型Fig.1 Probabilistic graphical model of MIMIC

1.2 混沌算法(CS)

在混沌优化算法中,通常选择Logistic映射所产生决策变量,其形式如下[4-5]:

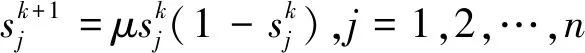
(1)

其中:μ为操控参数,当μ=4时,处于完全混沌的状态,且xn在(0,1)范围内是遍历的。

混沌搜索算法步骤如下:

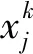
1.3 变尺度搜索(MS)

1.3.1搜索空间映射

由Logistic映射所产生的决策变量xn∈[0,1]必须映射到向量空间,即混沌搜索的上限和下限[a,b]。本文采用的映射公式如下[6]:

x′n=ci+dixn

(2)

式中，ci和di为与边界有关的系数,ci=a，di=b-a.

1.3.2变尺度搜索

以当前最优解x*为中心,通过[7-9]

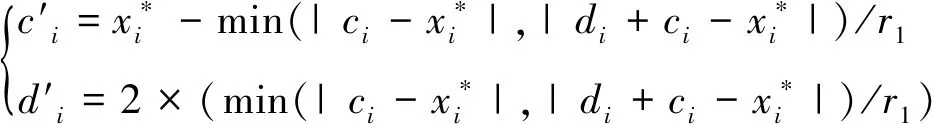
(3)

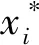
(4)

(5)

将式(5)和a=ci，b=ci+di分别代入式(3)即得式(2)。

图2 变尺度搜索示意图Fig.2 Schematic diagram of mutative scale optimizing search

1.4 MSCS-MIMIC算法

混沌搜索算法与MIMIC算法结合,旨在解决MIMIC算法局部搜索问题和CS算法对初值的高要求问题[10-11],在算法中引入变尺度搜索,可以重构优化变量取值空间,大大提高了结果的准确性。

算法实现过程如下:

步骤1:随机生成若干个体组成初始种群N。

步骤2:评估初始群N,如果连续搜索至相同值或找到最终的最优解,算法结束,否则进入下一步骤。

步骤3:使用截断选择、轮赌选择,将S个变量选出作为主导变量群,其中S=N/2。

步骤4:按照贪婪算法构建优势模型:

a.根据in=argminjhl(Xj)找出排列π=(i1,i2,…,in)中的in；

b.对任意k=n-1,…，1,根据ik=argminjhl(Xj|Xk+1),其中k≠ik+1…,in，计算出排列π=(i1,i2，…,in)；

步骤5:优势群体用CS算法进行搜索,对搜索后的优化值进行评价,并更新已知的最优值[12]。

步骤6:使用变尺度方法略微减小变量的取值区间,即以当前最优解为中心,通过(3)式所述,调整ci和di来重构优化变量的值空间。

步骤7:合并种群,将根据模型产生的优势变量与保留的优势群体组成新的种群,转到步2。

2 算法性能测试及分析

2.1 参数设置

为检测新算法的性能,并与CS-MIMIC算法、MIMIC算法比对,对下面6个无约束函数进行检验[13]。

在实验中,MIMIC算法的参数设置如下[14]:群体数量N=300,截断选择为N/2,最大迭代次数范围[10,50],这里选择30次。进行混沌搜索法的迭代次数为30次,对优势群体的20%进行迭代实验。

函数1:

minf(x)=f(1,1,…,1)=0

函数2:

minf(x)=f(0,0,…,0)=-105

函数3:

函数4:

minf(x)=f(0,0,…,0)=0

函数5:

minf(x)=f(0,0,…,0)=0

2.2 实验结果及分析

本文通过三种情况对实验数据进行归纳总结,得出MSCS-MIMIC算法的优势。

1)在种群更新代数、迭代次数以及维数相同的情况下,三种算法是不是能够收敛到最优解。本文取更新代数为200,迭代次数30次,维数M=2。

表1 200代内算法优化所得结果Table 1 The results of optimization within 200 generations

表1显示了三种算法进行30次独立实验的结果。可以看出,对于测试函数f1,MIMIC算法收敛到了最优值,而MSCS-MIMIC算法以CS-MIMIC算法更高的精度收敛到最优值附近,说明引入变尺度算法提高了新算法的收敛能力。其余函数,第一、二种算法的搜索结果对应于函数的最佳值,而MIMIC算法只找到了f2的最佳值。

2)在维数不变的情况下,算法运行结束后进化代数的均值。取维数M=2,进化代数为200。

表2 到达确定最优值的平均进化代数

表2是三种算法平均进化代数的比较结果。可以看出,MSCS-MIMIC算法的结果都较小,其中对于函数1,MSCS-MIMIC算法精度更高的前提下,算法的平均进化代数更小,这与算法中引入混沌搜索算法有很大的关系。而且在其余函数的试验中,MSCS-MIMIC算法都在收敛到最优值的前提下,运行了更少的进化代数。

3 结论

基于变尺度搜索算法的混沌MIMIC算法(MSCS-MIMIC)不仅继承了CS-MIMIC算法寻优能力高和运行速度快的特点,此外它还提升了算法的细化能力和稳定性,是一种有效的优化算法。从两组实验得出的数据可以看出,结合了变尺度搜索算法的混沌MIMIC算法能够以较高的精度收敛到最优值附近,或者直接收敛到全局最优值,并且最优值可以在较小的进化代数内找到,这对改进类似优化算法提出一种新的尝试。