投影法求解电场强度在竞赛中的应用

陈泽南 陈 辉

(永康市第一中学,浙江 金华 321300)

不同电荷分布下电场强度的求解是物理竞赛中考察的重点和难点.它对学生的数形结合分析能力及基本物理思想方法的运用要求较高．高斯定理是求解电场强度的重要方法,常见的还有微元法、对称法及电镜法等,适用条件各不相同,需具体问题具体分析．[1]

投影法是指将某一带电体上特定分布的电荷在某处产生电场与向某个方向投影后另一种分布的电荷产生电场等效来求解电场强度的方法．本文浅谈用投影法求解弧形分布、直线分布、球面分布及平面分布等情况下的电场强度．具体如下.

1 投影法求解弧形分布电荷的电场强度

例1.设半圆环型导体半径为r,正电荷均匀分布,线密度为η,求圆心处的场强．

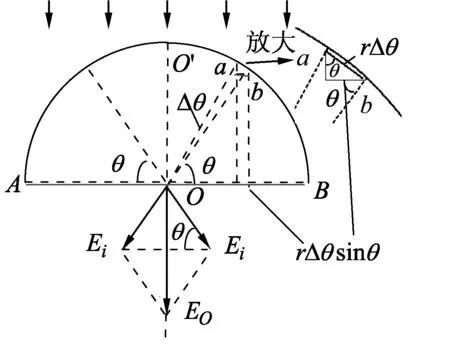
图1

解析:在半圆环上取极短的一段弧ab,长度为Δl=rΔθ,所带的电荷Δq=ηΔl,可视为点电荷．该弧ab对应的半径与水平方向成θ角．弧ab在O点产生的场强

由对称性可知,半圆环在O点的合场强方向沿着O′O方向,所以

其中rΔθsinθ可以看成弧长ab在AB方向的投影,则∑rΔθsinθ就是半圆在水平方向的投影——直径AB,即

∑rΔθsinθ=2r.

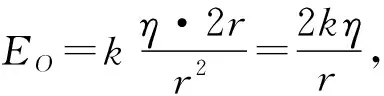
半圆环型导体在圆心产生的场强，等效成导体在垂直对称轴的投影形成的导体AB所具有的电荷η·2r集中于对称轴上离O点为r的位置O′在圆心O产生的场强．

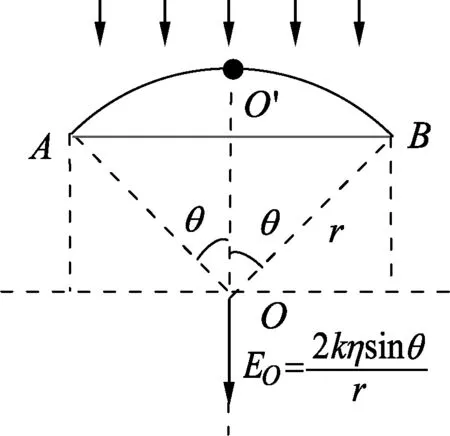
图2

拓展例1.弧形导体AB半径为r,正电荷均匀分布,线密度为η,在圆心处产生的场强等效成弦AB长的导体所具有的电荷η·2rsinθ集中于对称轴上离O点为r的位置O′在圆心O产生的场强，

方向沿O′O方向.

2 投影法求解直线分布电荷的电场强度

例2.如图2所示,一根无限长直导线,电荷均匀分布,电荷线密度为η,求距离该导线为r的O点的场强．

图3

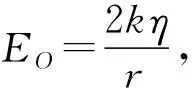
图4

拓展例2.一根有限长直导线,正电荷均匀分布,电荷线密度为η,离导线距离为r的O点的场强可以等效成导线AB向O点投影形成的弧ab在O点的场强．该点的场强可以用拓展例题1的结论来求解,

方向沿着弧ab的对称轴O′O,由O′指向O．

3 投影法求解球面分布电荷的电场强度

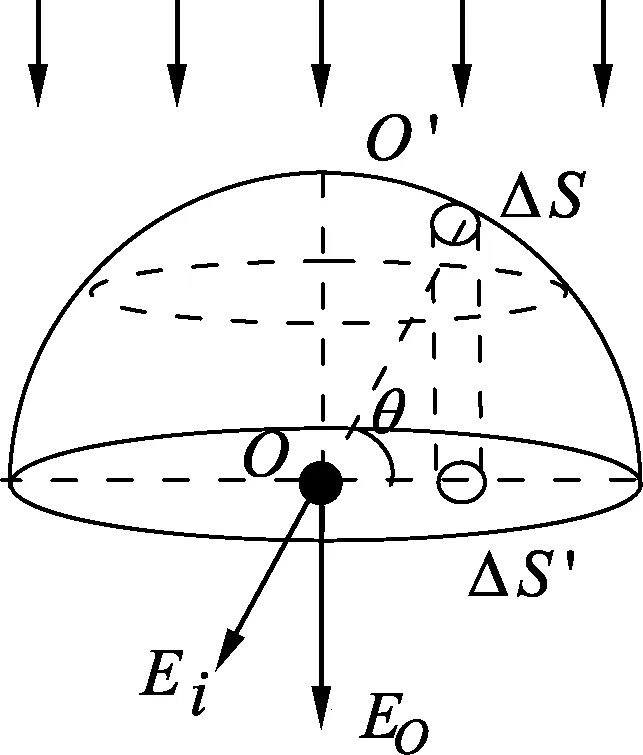
图5

例3.一半径为r的半球面均匀带正电,电荷面密度为σ．求球心处的电场强度．

解析:在半球面上取极小的一块球面ΔS,所带的电荷Δq=σΔS,可视为点电荷．该球面ΔS与O点的连线与水平方向成θ角．球面ΔS在O点产生的场强

由对称性可知,半球面在O点的合场强方向沿着O′O方向,所以

其中ΔSsinθ可以看成球面ΔS在水平面上的投影ΔS′,则∑ΔSsinθ就是半球面在水平方向的投影——圆面πr2,即∑ΔSsinθ=πr2.

图6

拓展例3.一半径为r的部分球面均匀带正电,电荷面密度为σ．球心处的电场强度，可以等效成部分球面在与对称轴垂直的面上的投影形成半径为rsinθ的圆面所具有的电荷σπ(rsinθ)2集中于对称轴上离O点为r的位置O′在圆心O产生的场强．

4 投影法求解平面分布电荷的电场强度

图7

例4.一无限大均匀带正电平面,电荷面密度为σ,求距平面距离为r的O处的电场强度．

解析:在平面上取极小的一块平面ΔS,所带的电荷Δq=σΔS,可视为点电荷．该平面ΔS到O点的距离为d,与O点的连线与竖直方向成θ角．球面ΔS在O点产生的场强

由对称性可知,无限大带电平面在O点的合场强方向沿着O′O方向,所以

其中ΔS′是ΔS在垂直与O点连线方向的投影.

其中ΔS″是ΔS与O点形成的锥体与半径为r的半球面相交的曲面,则∑ΔS″就是将无穷大的平面与O点形成的锥体与半径为r的半球面相交得到的曲面,即半球面的面积——2πr2,即∑ΔS=2πr2.

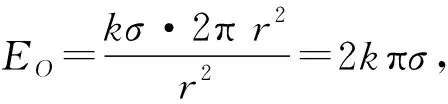
5 结束语

弧形(球面)分布电荷产生的电场强度可以等效为与对称轴垂直的直线(平面)投影形成的线段或圆面所具有的电荷集中于对称轴上离O点为r的位置O′在圆心O产生的场强．而直线(平面)分布电荷产生的电场强度可以等效为O点投影形成的半径为r的部分圆弧(球面)所具有的电荷集中于对称轴上离O点为r的位置O′在圆心O产生的场强．通过以上几种模型的讨论与思考,对提升竞赛中学生数结合分析能力及物理思想方法有积极作用．