电感和电容对交变电流影响的深入剖析

2019-09-23涂德新

物理教师 2019年7期

涂德新

(江西师范大学附属中学,江西南昌 330046)

在一次教研活动中,有位青年教师上了一节题为“电感和电容对交变电流的影响”的公开课,课后有位教师提出:“请问如何理解一个周期内,当电流增加时,电感阻碍交变电流的增加,这是阻碍;当电流减小时,电感阻碍交变电流的减小,这也是阻碍交变电流通过吗?如何准确理解“阻碍”二字?”该青年教师一时语塞．现场很多教师也参与讨论,没有一个准确的结论．可见这个问题是很多物理教师专业知识的“盲区”．

1 教学疑惑

笔者经过认真收集整理,发现很多教师可能在教学研究过程中存在下面的一些疑惑．

疑惑1:电感对交变电流的影响．如果电流在增加,则由于自感而产生的自感电动势阻碍电流的增加,这是很自然的．如果电流在减小,则由于自感而产生的自感电动势阻碍电流的减小．这种情况下还是电感阻碍交变电流通过吗?如何准确理解电感的阻碍作用?

疑惑2:电容对交变电流的影响．如果电源电压增加,则电容器充电,于是电容器的电压增加;如果电源电压在减小,则电容器放电,于是电容器的电压也减小．是不是说电源的电压和电容器的电压同步变化,即同时增加,同时减小?

疑惑3:电感的感抗公式XL=ωL以及电容的容抗公式XC=(ωC)-1是怎么来的,有何理论依据?

疑惑4:电容器两个极板是绝缘的,不可能有自由电荷通过,如何准确理解课本上说的“表现为交变电流“通过”了电容器”?[1]

2 理论分析

要解答以上的疑惑,我们先从理论上推导一下电感和电容对交变电流的影响．

2.1 电感对交变电流的影响

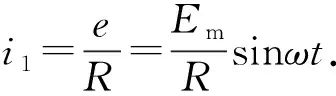
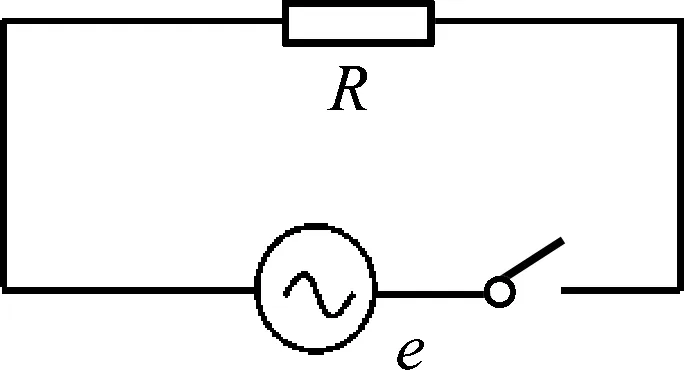
图1 图2

由常数变易法可得这个一阶微分方程的解

可以求得

再查积分公式表可以得到

化简得

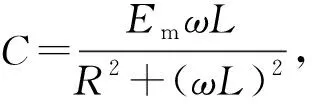
经过足够长的时间稳定后

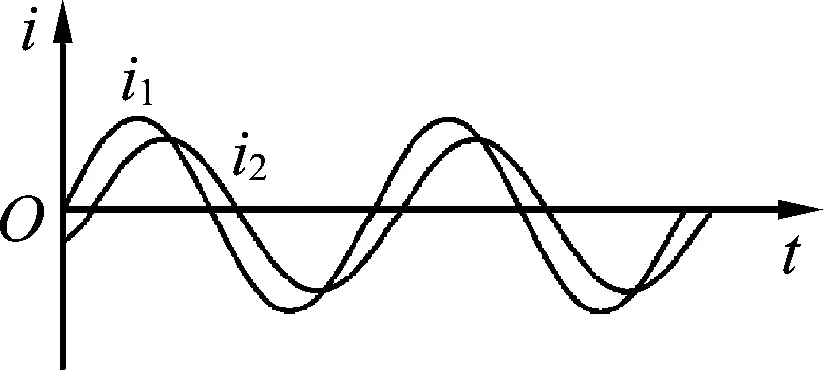
图3

如图3所示,在一个坐标系中画出稳定后i1和i2的图像．与示波器直接观察的实验现象一致．[2]

2.2 电容对交变电流的影响

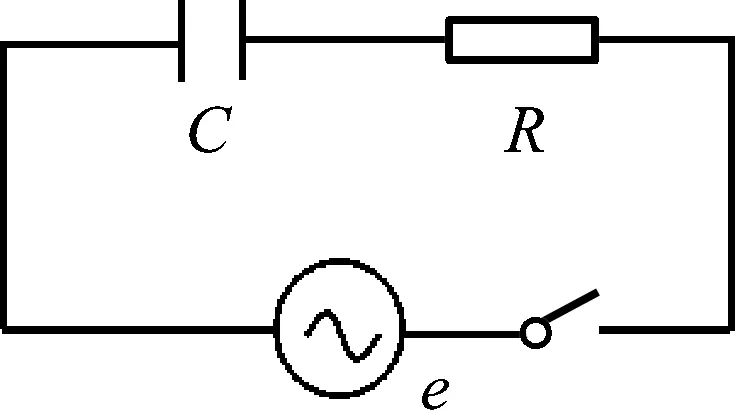
图4

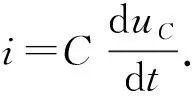
同电感类似的方法可以求得

经过足够长的时间稳定后

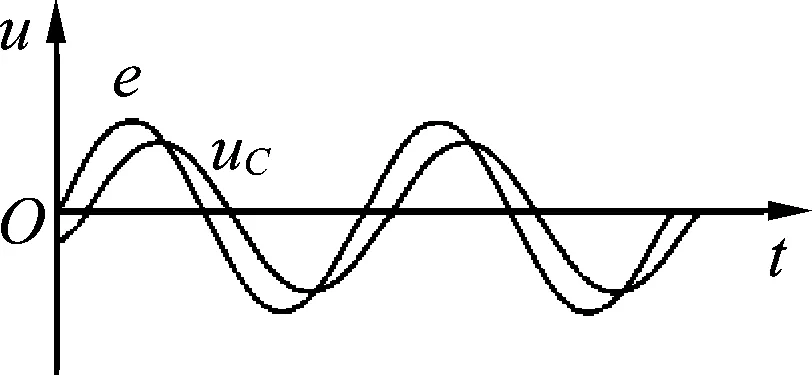
图5

其中tanφ=RωC.

如图5所示,在一个坐标系中画出稳定后e和uC的图像．

2.3 位移电流

图6

当然此处是简易的推导,详尽的理论推导请查阅有关文献,[3]不过这个简易的推导通俗易懂,可以解决教学疑惑．

3 解疑释惑

释疑1:由图3可知,电感对交变电流瞬时值的作用比较复杂,没有电感时为i1,有电感时变为i2.可以发现电感线圈有时阻碍交变电流瞬时值的增加,有时阻碍交变电流瞬时值的减小.当然一个周期整体上是阻碍交变电流的通过,阻碍最本质的特征是体现在峰值的减小,这是准确理解阻碍的核心．

释疑2:不能简单地认为电源的电压增加,则电容充电,电源的电压减小,则电容放电．二者不是同步进行,存在相位差,由图5可知,电源电压增加时,电容可能充电,也可能放电,反之亦然．

释疑3:分析有电感时电流峰值的表达式可以发现,ωL和电阻R处于同等地位,有相同的单位欧姆,有理由认为电感对交变电流的阻碍即感抗XL=ωL,不过电感与电阻的串联不能简单地把感抗和电阻相加．同理分析出电容对交变电流的阻碍即容抗为XC=(ωC)-1．

释疑4:电容器接入交变电流时,电容器会反复的充放电,于是电容器中存在变化的电场.英国物理学家麦克斯韦首先提出这种变化的电场对应的电流为“位移电流”,并假设变化的电场也会激发磁场．但位移电流只表示电场的变化率,与传导电流不同,它不产生热效应、化学效应等．但它引起的磁场与传导电流引起的磁场等效．理论和实践表明位移电流的假设是正确的．