高铁驱动齿轮箱稳态温度场分析建模与仿真*

(北方工业大学机械与材料工程学院 北京 100144)

驱动齿轮箱是高铁动力系统的关键部件，发热问题是其显著特点。齿轮箱采用飞溅润滑方式，高速运转摩擦副产生的功率损失大部分转化为热能，箱体内部温度会迅速上升，导致箱体内润滑油黏度下降，油膜厚度减小，造成齿轮和轴承的润滑条件恶化，降低传动效率并影响零部件的使用寿命和可靠性，严重时会导致轴承温度超过预警值，迫使高铁降速运行甚至中途交路换乘，影响高铁运行准点率和运行计划。此外，高温不仅导致轴承游隙减小，增大了发生热轴故障的可能性，而且也会导致齿轮发生胶合、齿面点蚀失效以及箱体热疲劳损伤[1-5]。因此，高铁驱动齿轮箱稳态温度场的影响因素及其影响规律分析，是保障高铁平稳、可靠运行的关键。

目前国内外关于高速齿轮箱温度场的研究主要包括3种方法：试验法，热网络法和有限元法。试验法一般采用热电偶或红外线温度计测量温度，成本高、周期长，通常用来标定热网络法和有限元法中的关键参数以提高计算精度，或者对计算结果进行验证[6]。葛世祥、黄飞[2,7]运用热网络法分别对行星减速器、GSS高速齿轮箱进行热分析，根据减速器内部零件之间的传热关系，建立减速器热流传递的网络模型并用MATLAB进行编程求解，但节点数量和节点位置的选择对计算精度影响较大。有限元法适应性广、计算效率高，在高速齿轮箱温度场分析中应用广泛。黄智勇、李亚丽[8-9]在计算齿轮、轴承、搅油等热源发热功率和齿轮箱内外表面对流换热系数的基础上，采用CFD软件仿真分析获得了齿轮箱整体及零部件的温度场分布云图和不同工况参数情况下的温度场变化规律。安达[10]在分析计算高速齿轮摩擦发热与对流换热的基础上，应用ANSYS仿真分析了齿轮参数、负载、转速等参数对齿轮本体温度的影响规律和程度。但文献[8-10]中没有探讨如何优选发热功率与对流换热系数计算公式中的有关系数以提高计算精度这一重要问题。

本文作者以某高铁齿轮箱传动结构为例，研究分析其产热与散热途径，建立温度场有限元分析模型并确立边界条件；根据试验数据优选发热功率计算参数，基于FLUENT流场分析监测数据精确计算了箱体内部轴承端面、齿轮等关键部位对流换热系数，考虑齿轮箱外部风场、行车速度、环境温度和注油量等因素的影响，分析了齿轮箱温度场分布及各因素的影响规律，为高铁的安全可靠运行及驱动齿轮箱润滑油流道结构改进设计提供重要参考。

1 热源与散热途径分析

高铁齿轮箱的热源与散热途径如图1所示。热源包括：齿轮啮合功率损失产生的热量，滚动轴承摩擦功率损失产生的热量和齿轮搅油功率损失产生的热量。齿轮箱各热源产生的热量通过多种方式传散：不同零件接触部位通过热传导方式传递热量，箱体内油气混合物与零件之间、箱体外部与外部环境之间通过对流换热方式传递热量。

2 温度场有限元分析模型及边界条件

2.1 外部风场分析模型及边界条件

为了分析风速对齿轮箱温度场的影响规律，需要在箱体外部施加风场。箱体外部流域几何模型及网格模型如图2所示，在ANSYS meshing模块中采用非结构体网格进行网格划分。选用标准k-ε湍流模型和标准壁面函数法模拟箱体外部风场空气流动。入口边界条件设置为速度入口(风速)，出口边界条件设置为压力出口，选择SIMPLE算法对能量方程离散求解。

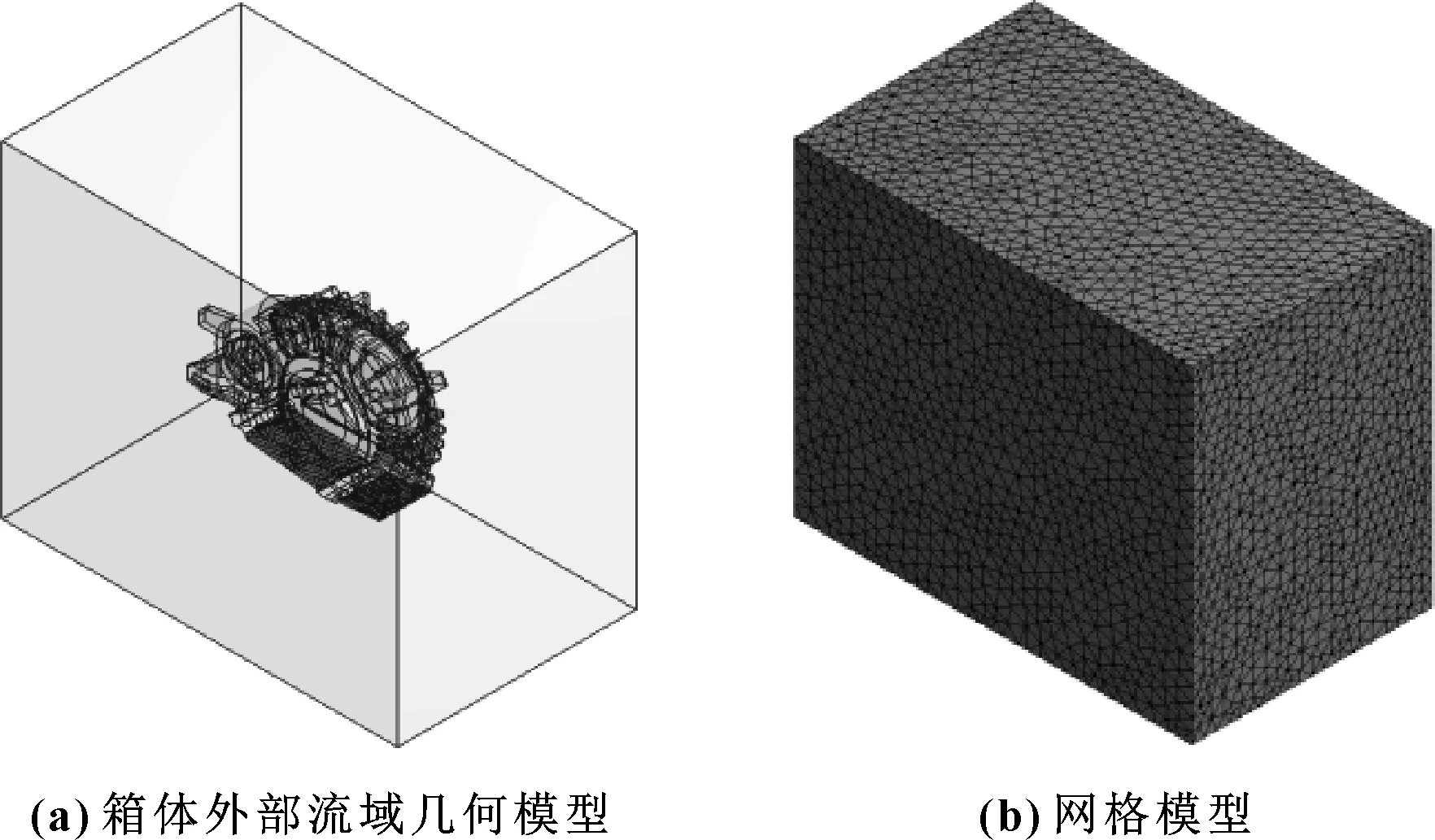
图2 齿轮箱外部风场模型

2.2 箱体温度场有限元分析模型及边界条件

在Solidworks中进行齿轮箱三维模型简化，去掉圆角、倒角等非重要结构元素，尽可能维持物理模型原样以保证计算精度。简化后将模型导入Workbench，使用meshing模块进行网格划分，对轴承、齿面等热源部位进行网格细化。为确保计算顺利进行，网格扭曲度一般控制在0.8以下。文中齿轮箱的网格单元数为1 662 753个，节点数为369 487个，网格扭曲度为0.785。箱体网格模型如图3所示。

图3 齿轮箱温度场有限元分析网格模型

箱体内部流域按体积比例设置为油、气两相流，选择标准k-ε湍流模型模拟箱体内油气混合物的流动状况。定义材料属性，加载热源生热率和对流换热系数，选择SIMPLE算法对能量方程离散求解。轴承内圈与轴、轴承外圈与箱体、齿轮与轴、小齿轮与大齿轮啮合点等接触部位按热传导方式设置，油气混合物与轴承端面、箱体内壁面、齿轮端面、齿面、箱体内轴的圆柱面之间按对流换热方式设置。

3 发热功率计算公式

3.1 轴承发热功率计算

轴承摩擦发热是齿轮箱的主要热源之一，与轴承摩擦力矩和转速有关。工程中常用Palmgren公式精确计算轴承摩擦力矩M[11]：

M=M0+M1

(1)

其中，M0是与轴承载荷无关的摩擦力矩。高速轻载场合，M0起主导作用。M0与轴承类型、润滑剂黏度和轴承转速有关。

vn≥2 000时：

(2)

vn<2 000时：

(3)

式中：v为轴承工作温度下润滑剂运动黏度，mm2/s；n为轴承转速，r/min；Dm为轴承平均直径，mm，Dm=0.5(d+D)；f0为与轴承类型和润滑方式有关的系数，高铁齿轮箱轴承f0=2～4。

M1是与轴承载荷有关的摩擦力矩。M1与弹性滞后、接触表面差动滑动的摩擦损耗有关，计算公式为

M1=f1F1Dm

(4)

式中：f1为与轴承类型和载荷有关的系数；F1为计算摩擦力矩时的轴承载荷，N。

根据轴承摩擦力矩和转速，轴承发热功率Pf计算公式[12]为

Pf=1.05×10-4Mn

(5)

3.2 齿轮啮合发热功率计算

齿轮啮合发热功率源于齿面滑动摩擦损失和滚动摩擦损失组成的啮合功率损失，其计算方法有ISO/TR14179法、Shipley法、Buckingham法和Anderson and Loewenthal法等。经试算对比，Anderson and Loewenthal法[13]比较适合高铁齿轮箱的啮合功率损失计算。

(1)齿面滑动摩擦功率损失计算

平均滑动摩擦损失计算公式为

Ps=fFnvs×10-3

(6)

式中:f为摩擦因数；vs为啮合处平均滑动速度，m/s；Fn为齿面法向载荷，N。

(7)

T1=9 550P/n1

(8)

(9)

(10)

式中：T1为主动齿轮输入转矩，N·m；r1、r2分别为主、从动齿轮分度圆半径，m；α为压力角，Rad；β为基圆螺旋角，Rad；P为输入功率，kW；n1为输入转速，r/min；gs为啮合线长度，m；Z1、Z2分别为主、从动轮齿数；ra1、ra2分别为主、从动轮齿顶圆半径，m；rb1、rb2分别为主、从动轮基圆半径，m。

(2)齿面滚动摩擦功率损失计算

(11)

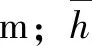
(12)

(13)

式中:u为润滑剂绝对黏度，Pa·S；WN为平均正压力，N；ρeq为曲率半径，m。

(14)

3.3 齿轮搅油发热功率计算

齿轮搅油发热功率与大齿轮的轮齿宽度b(m)、浸油深度h(m)、节圆线速度v(m/s)等有关，根据余联庆经验公式计算[15]：

P=347.5bhv1.5

(15)

v=πr2n2/30

(16)

式中：n2为大齿轮转速，r/min。

4 基于流场分析监测数据的对流换热系数计算

箱体壁面、齿轮齿面和端面、轴承端面等关键部位对流换热系数的精确计算，是高铁齿轮箱温度场精确计算的关键之一。文中提出了一种基于流场分析监测数据的对流换热系数计算方法，即先进行流场分析，监测关键部位的润滑油体积分数、流速，然后根据油气比例及物性参数计算对流换热系数。

油气混合物的物性参数ξf[16]为

ξf=αaξa+αoξo

(17)

式中：ξo、ξa分别为润滑油、空气的物性参数；αo、αa分别为润滑油、空气的体积分数，αa=1-αo。

4.1 箱体对流换热系数计算

箱体内壁面对流换热系数h1的计算，采用不可压缩流体与平板强迫对流换热计算公式[17]：

(18)

(19)

(20)

式中：λ为箱体内油气混合气导热系数，W/(m·K)；l为箱体壁面特征长度，m；Re为雷诺数；u为油气混合气流动特征速度，m/s；v为油气混合气运动黏度，mm2/s；c为油气混合气比热容，J/(kg·K)；ρ为油气混合气密度，kg/m3。

箱体外壁面对流换热系数根据图1所示外部风场模型，设定风速后由FLUENT软件自动计算。

4.2 齿轮和轴承对流换热系数计算

齿轮对流换热系数包括齿轮齿面和端面2个部分。齿面对流换热系数h2计算公式[11]为

(21)

式中：l为特征长度(取齿轮分度圆直径)，m。

齿轮端面和轴承端面按圆盘端面处理，端面对流换热系数h3计算公式[18]为

(22)

式中:m为指数常数，m=2；ω为转速，rad/s；rc为端面任意半径，m。

由式(22)可知：齿轮端面和轴承端面不同半径处的对流换热系数不同，为便于计算时端面对流换热系数的施加，h3为rc取值范围内的平均对流换热系数。

5 稳态温度场仿真试算及发热功率公式系数优选

根据上述有限元分析模型、发热功率及对流换热系数计算方法，进行稳态温度场的仿真试算，发现f0对稳态温度的影响较大，结合试验温度对f0进行优选，以提高后续仿真计算精度。试算结果如表1所示。其中，PW表示高速轴车轮侧，有两个位置PW1和PW2，PM表示高速轴电机侧，GW表示低速轴车轮侧，GM表示低速轴电机侧，括号内数字为轴承编号。

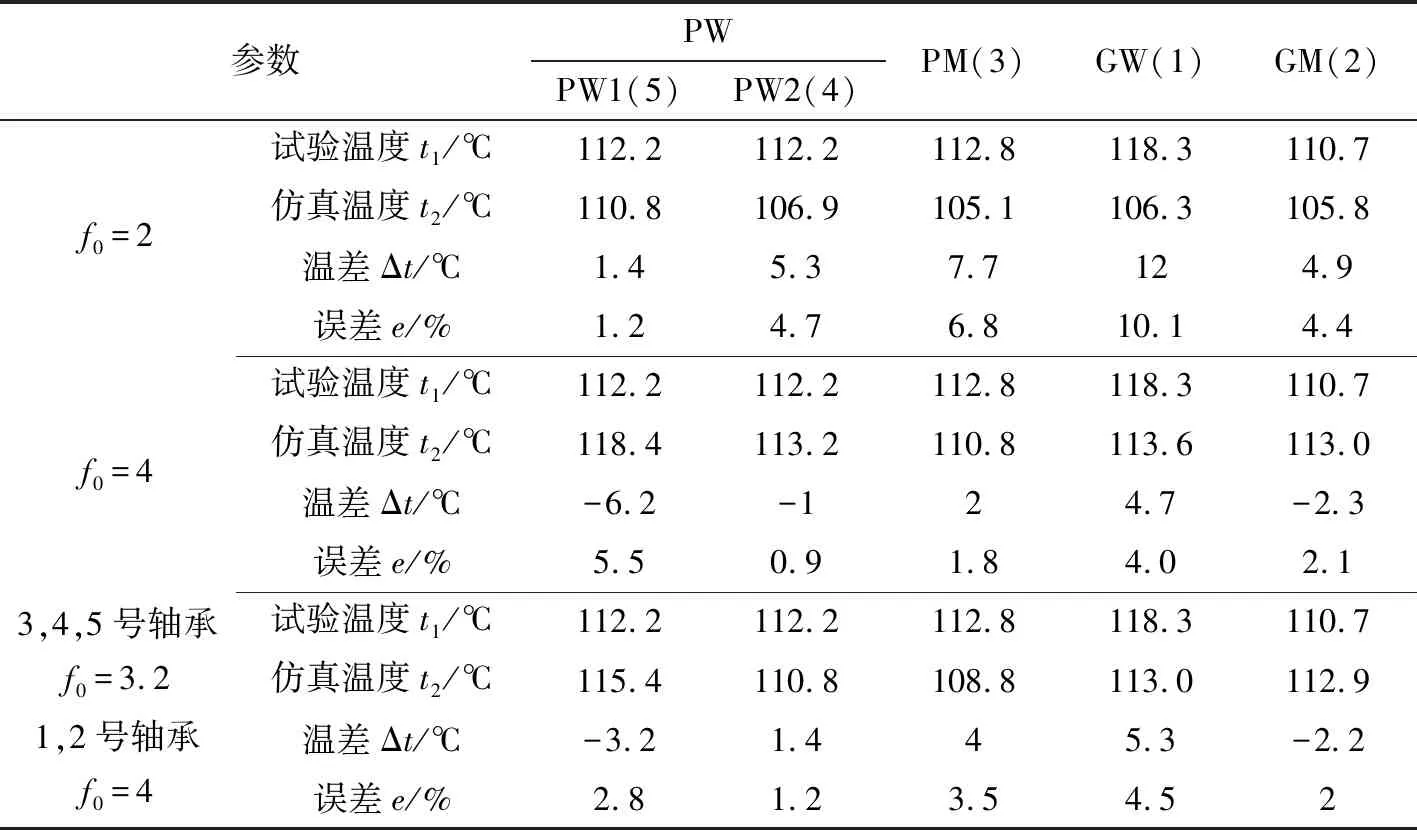
表1 发热功率计算公式系数f0优选

由表1可知：当高速轴轴承取f0=3.2，低速轴轴承取f0=4时，轴承温度仿真计算值与试验值误差最大为4.5%，最小为1.2%，可以满足工程计算要求。

6 稳态温度场影响因素仿真分析

根据上述模型及计算方法，采用正交仿真分析法，研究行车速度、风速、环境温度、注油量等因素对齿轮箱稳态温度场的影响规律。仿真因素-水平如表2所示。仿真结果与极差如表3所示。

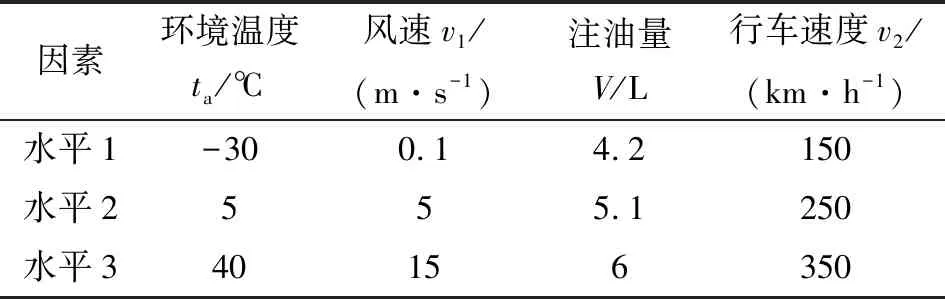
表2 仿真因素-水平正交表

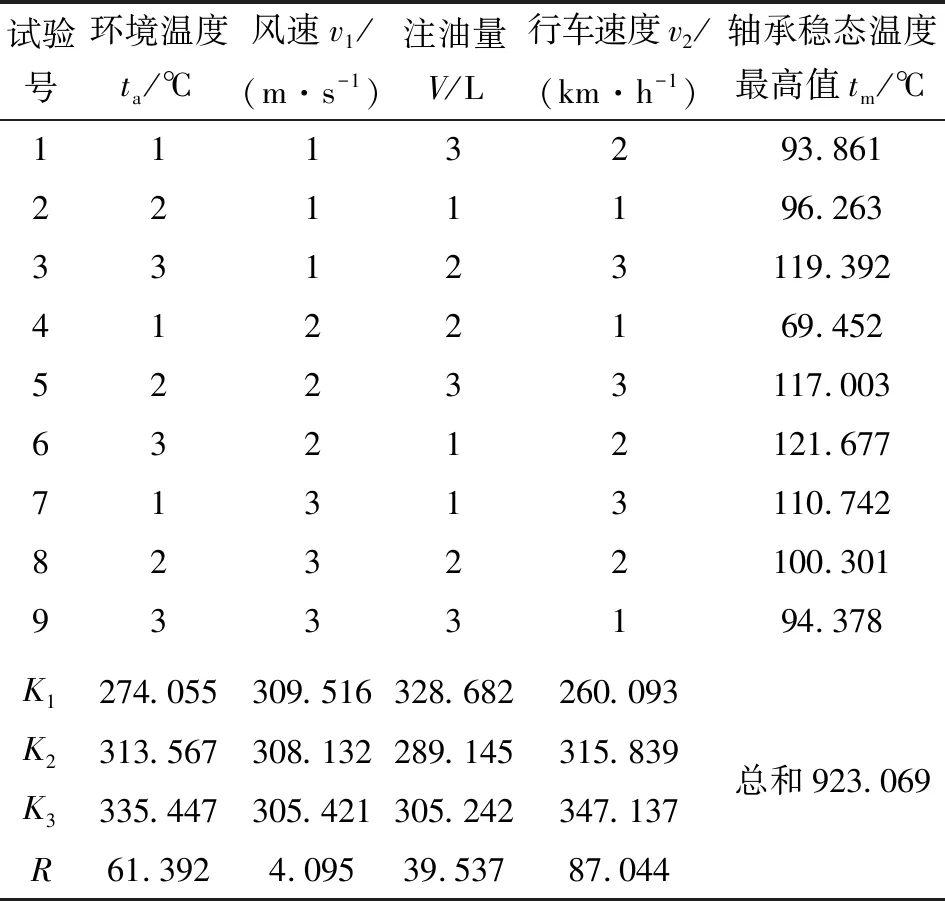
表3 仿真结果与极差分析表

由表3可知：诸因素对轴承稳态温度影响程度从高到低的次序为行车速度、环境温度、注油量和风速。轴承最高温度随各因素变化的趋势如图4所示。轴承最高温度随行车速度、环境温度的增加而上升，随风速的增加而下降；轴承最高温度随注油量的增加，先下降后上升，表明高铁齿轮箱存在最佳注油量，与高铁实际运行情况相符，原因是注油量偏少时润滑不足、注油量偏多时搅油发热增加，两者均会导致轴承温度升高。

图5所示为行车速度250 km/h、注油量6 L、环境温度-30 ℃、风速0.1 m/s时的各轴承稳态温度场分布云图。

图4 轴承稳态最高温度随环境温度、风速、注油量和行车速度的变化

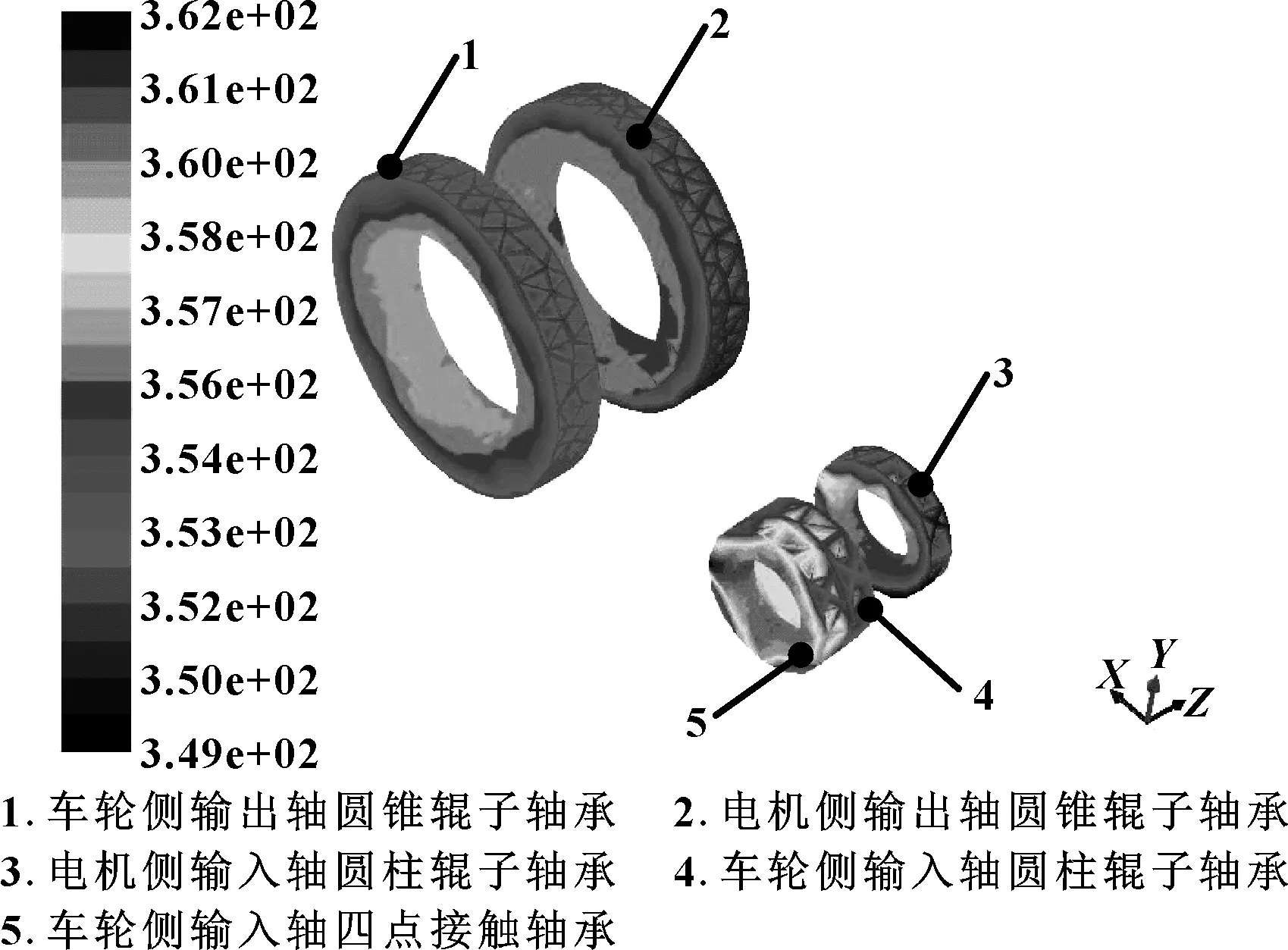
图5 轴承稳态温度场云图

由图5可知：4号、5号轴承的最高温度高于其他轴承，一是因为这2个轴承之间端面用隔套隔开，隔套与轴承端面只能通过热传导而非对流换热方式散热，散热速度较慢；二是因为2个轴承摩擦发热，相当于2个热源紧挨在一起，热流密度较高。另外，轴承外圈温度均低于内圈温度，主要是因为外圈与铝合金箱体接触，导热快；内圈与钢质车轮轴接触，导热相对较慢。在运行工况不变的情况下，轴承端面的温度随轴承腔内油的比例的增加而降低。

7 结论

(1)运行工况参数对高铁驱动齿轮箱的稳态温度分布有重要影响，影响程度从大到小的顺序依次为行车速度、环境温度、注油量和风速。

(2)轴承温度随行车速度、环境温度的增加而升高，随风速的增大而降低，但风速影响较小。随着注油量的增加，轴承温度呈现先降低后升高的趋势，因此注油量过多或过少，都会导致轴承温度升高。

(3)结合齿轮箱试验温度对发热量计算公式进行参数优选，并根据流场分析监测数据计算对流换热系数的方法，可以提高齿轮箱温度场分析计算精度，计算误差小于5%，可以满足工程分析计算要求，也可用于检验润滑油流道改进设计对温度场的影响效果。