改进的Harris算法在海洋遥感图像处理中的应用

刘军泉，刘晓华，黄小仙

（1.中国科学院大学，北京 100039；2.中国科学院上海技术物理研究所，上海 200083；3.中国科学院红外探测与成像技术重点实验室，上海 200083）

0 引 言

角点是包含了图像的重要特征信息的点，角点检测算法也是热门的图像算法。角点检测算法在目标识别与跟踪、全景拼接、图像配准、相机标定、运动估计、电子稳像等多个领域内起着重要的作用[1]。

我国与巴西在1999年合作成功发射“资源一号”卫星，建立了自己的遥感数据采集系统，推动了国内遥感技术发展。随着数据融合的兴起，遥感数据融合也成为热门，广泛应用于地理探测与规划、军事国防、植被农业评估和环境污染等领域，而遥感图像配准是其中关键技术[2]。此外，基于特征[3]（尤其是角点）的图像检测算法极具实用前景，已经成为研究的主要方向和发展趋势。

为了克服基于传统Harris 角点检测算法带来的漏检、定位精度差等问题，本文提出一种改进Harris 角点检测算法。Harris 算子虽然具有旋转不变性，但它不具备尺度不变性而且抗噪声性能差[4]。对此本文引入双边滤波，可以减少噪声的干扰；同时引入高斯尺度空间，使得Harris 算子具有尺度不变性。但多尺度算法往往容易产生角点冗余，所以本文最后针对候选点集产生机理来分组检测以及剔除多余角点并选取最佳角点，提高定位精度和降低漏检率。

1 Harris角点检测原理

Harris算子是C.G.Harris和M.Stephens 在1988年提出的一种基于灰度强度变化的提取点特征的算子[5]。设f(x,y)为图像函数，Ix，Iy为图像函数在x，y方向的偏导数，定义其自相关矩阵为：

式中：“⊗”符号代表卷积；w代表高斯滤波函数：

当Mh的两个特征值均较大时，说明该点周围发生了较大的灰度变化，可认为该处是角点。为了减少计算量，避免对矩阵进行特征分解，引入角点响应函数（CRF）：

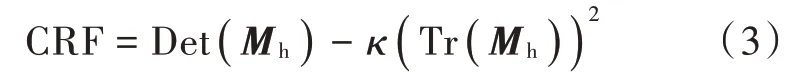
2 改进的Harris算法

2.1 尺度空间理论

由于传统Harris 算法尺度单一，弱角点难以检测，易造成漏检，尺度空间的引入是一个很好的解决方法。文献[6-7]论证了高斯核函数是尺度空间的唯一线性卷积核，二维高斯函数定义如下：

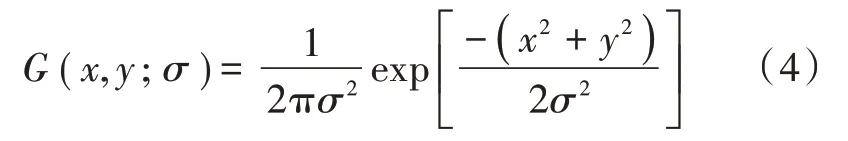
多尺度Harris 检测算法即为引入高斯核函数后的Harris 检测算法，由于多尺度Harris 角点检测时没有很好的角点筛选机制，很容易形成冗余点过多的情况。对此，文献[8]用LOG 算子来去除冗余点，其原理是在图像多尺度表示下建立多尺度的角点集，在局部尺度中使LOG 算子达到极大值的角点作为最终角点，称为Harris-Laplace 方 法。LOG 算子定 义如下[9-10]：

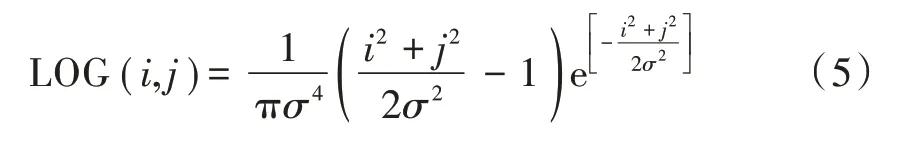
2.2 双边滤波下的多尺度检测

双边滤波[11]是一种非线性的平滑滤波，在Harris 角点检测预处理过程中，用双边滤波器代替了传统的高斯滤波器，实现了图像去噪后的边缘保持效果，减少了噪声影响下的角点丢失情况发生，提高了算法的精度同时降低了误检率。双边滤波同时考虑了空间域和灰度域的权值，表达式如下[12]：

将式（6）代入式（3）可以得到新的双边滤波自相关矩阵：

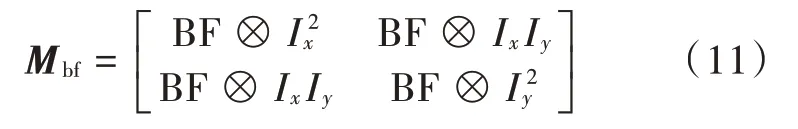
然后利用高斯核函数对图像进行尺度分解，通过式（11）得到多尺度双边滤波自相关矩阵：

式中：σD是积分尺度；σI是微分尺度是对应方向的高斯函数卷积的结果。

将Mmbf代入式（3），得到新的具有尺度的响应函数为：

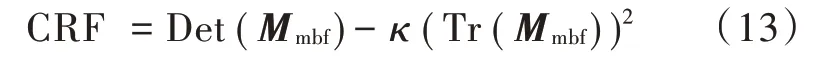
本文利用Harris-Laplace 算法中的LOG 算子来选取候选角点集。下面来讲解如何从中选取出最佳角点集。

2.3 最佳角点的选取

同多尺度Harris 算法和Harris-Laplace 算法一样，多尺度双边滤波也会产生冗余角点。本文针对候选角点产生的机理，相应的冗余角点分为两类：一类是多个尺度空间表示同一位置的角点；另一类是多个尺度空间表示同一角点时定位上出现了差异。情况如图1a）、图1b）所示。对此问题，本文提出一种将图像按区域分组的解决方法，同一区域为同一组，每组保留一个最佳角点，具体如下：

1）考虑到LOG 函数取得的候选角点中可能有多个尺度空间表示同一位置角点的情况，在此选择相同位置的角点只保留最小尺度空间的那一个，最后记录下所有角点的位置坐标，为后面分组筛选消除了部分冗余角点。

2）为了提高检测效率，只对存在角点的区域分组，同一组区域内可能存在多个尺度检测出的角点，因为经过前面几个步骤的筛选，现在同一组内的冗余角点还有可能是因为不同尺度空间定位同一角点时位置上有一定误差。对此之后都取15×15 大小的模版作为角点的组内邻域空间，同一组内选取尺度最小的角点作为该组最终角点。因为尺度越小，角点定位越精确，角点离原始图像越接近，它包含的信息越多，直到所有的组都经过验证，并且获得每个组中的最终角点。

图1 LOG 算子产生的两类典型冗余角点机理示意图Fig.1 Mechanism schematic diagram of two kinds of typical redundant corner points generated by LOG operator

3 实验结果与分析

为验证本算法的实际效用，在Windows 10 环境下采用Matlab 软件对blocks 标准测试图进行测试，测试过程中选择13 个尺度空间，各个微分尺度定义如下[8]：

式中：s=0.7；σ1=1.5；τ=1.2。本算法双边滤波函数中的空间尺度σs=2，灰度尺度σg=0.05。

3.1 算法有效性

角点查全率、查准率可定义为：查全率R=a b，查准率：P=a/c，a表示检测到的正确角点数，b为图像实际的角点数，c为检测到的角点数[13]。本实验中对经典Harris算法、Harris-Laplace 算法以及本文算法进行检测结果比较，选用的图片的正确特征点个数为60 个，实验结果如图2所示。各算法对应的查全率、查准率如表1所示。由数据分析可知，Harris算法比Harris-Laplace的查全率低，但是查准率比Harris-Laplace 高，说明Harris-Laplace 虽然算法引入多尺度思想比传统Harris算法可以检测出更多正确角点，但是随之而来的伪角点影响却不能很好排除。本文算法的查准率只比传统Harris 算法稍低，但是查全率比其他两种算法都高。

3.2 算法在遥感图像的配准中的对比结果

本文的图像配准算法采用常用的基于角点的匹配算法，主要步骤分成两步：角点提取和角点匹配。角点坐标由本文算法提供，特征匹配采用[14]文中提出的基于改进的RANSAC（随机抽样一致）点集匹配算法。图3a）为我国HY-1B 海洋水色遥感卫星的两幅资源图，左半部分图像摄于 2011年 5 月 27 日下午北京时间 17：26 过美国加利福尼亚州时第7 可见光通道（730～770 nm）的局部图像，左半部分图像摄于2011年5 月28 日下午北京时间17：24 过美国加利福尼亚州时第6 可见光通道（660～680 nm）的局部图像。图3b）为Harris-Laplace算法得到的角点集特征匹配效果图，图3c）为多尺度Harris 算法得到的角点集特征匹配效果图，图3d）为本文算法得到的角点集特征匹配效果图。

由表2数据可得知，本文算法可以有效去除冗余角点，并且由图3d）、图3c）也可知本文算法可以更有效地检测出弱角点，从图3d）最上方那组匹配的角点便可以看出。综上可得，本文算法不仅可以提高角点检测率还能同时保证定位精度，得到效果比传统的Harris 和Harris-Laplace 算法更好。

4 结 论

本文通过研究利用多尺度Harris 算法和Harris-Laplace 算法进行海洋水色扫描仪遥测图像处理过程中发现这两种算法在海岸线轮廓数据分类检测时均存在冗余点过多的问题。问题的原因在于在多尺度空间条件下，缺乏对冗余角点的重复剔除机制。

图3 算法的去冗余结果对比Fig.3 Comparison of redundancy removal results of three algorithms

表2 匹配算法的去冗余点比较Table 2 Comparison of redundancy points removal of matching algorithm

本文在传统Harris角点检测算法的基础上提出一种改进的Harris 检测算法，本算法克服了传统Harris 算法对弱角点易漏检的问题，又比多尺度Harris 算法与Harris-Laplace 算法能更好地去除冗余角点，并对海岸带轮廓图像实现了较好的角点匹配，为今后对HY-1B 水色图像的水域数据分类检测提供了良好的定位。