高压电力电缆配电线路故障在线检测方法研究

章以建

（浙江大学，浙江 杭州 310027）

0 引 言

高压电力电缆配电线路承担传输电力的重任，是供电网络命脉，在节能环保、经济发展理念的带动下，低耗能、高传输率和长距离传输特点的高压电力电缆是未来电力发展的主要方向。高压电力电缆配电线路由于长期在极端恶劣条件下运行，如高寒地区、极端天气和地质灾害等，其发生故障概率较高[1]，发生配电线路故障对人们日常生活和工农业生产造成巨大影响，所以快速、准确地对高压电力电缆配电线路故障进行精确地在线检测，减少断电时间，提升供电可能性十分必要[2]。

本文深入研究高压电力电缆配电线路故障在线检测方法，不仅检测出故障位置，还检测出故障位置线路两端的电容值，提升配电线路故障检测精度与速度，降低错误故障检测和遗漏故障检测发生概率。

1 配电线路故障在线检测方法

1.1 基于行波故障位置检测

1.1.1 已知行波速度的故障在线检测

当已知高压电力电缆配电线路故障处行波速度r时，可采用故障初始行波到配电线路端点时间运算故障发生位置，其运算原理如下：假设该高压电力电缆某配电线路长度为L，故障发生位置距配电线路两端P和Q距离（单位：km）分别为p和L-p，初始故障行波到配电线路两端点时间分别为s和s′。高压电力电缆配电线路故障示意图如图1所示，则存在：

且根据式（1）可得：

该方法均适用配电线路发生接地和非接地故障，且其运行前提是行波速度r已知。实际高压电力电缆配电线路中行波速度受到多种因素影响[3]，包括配电线路分布电感G1、分布电容R0和土地电阻率。因此对于不同高压电力电缆配电线路故障，行波速度r均不相同，而将光速视作行波速度会导致高压电力电缆配电线路故障在线检测出现误差[4]。

图1 高压电力电缆配电线路故障示意图Fig.1 Diagram for distribution line fault of high-voltage power cable

1.1.2 未知行波速度的故障在线检测

当高压电力电缆配电线路故障发生处的行波速度未知时，可通过检测线模和零模分量到P和Q点的时间实现故障在线检测。该方法可降低行波对故障检测造成的误差[5-6]。同样以图1高压电力电缆配电线路故障示意图为例，将线模和零模行波的速度分别用r1和r0表示，将故障行波的线模分量到P和Q端点时间分别用s0和表示，零模分量到P和Q端点时间分别为s1和，关系如下：

联立式（3）～式（5），得到：

当高压电力电缆配电线路发生非接地故障时，此时不存在零模分量，不存在s1和，式（6）仅能用于测量接地故障[7]，但高压电力电缆配电线路相间间隔较大，所以配电线路故障类型通常为单相接地故障，因此该方法用于故障测距同样具有应用价值。

1.2 故障位置处电阻值检测

将第1.1 节检测到的高压电力电缆配电线路故障发生位置处的配电线路两端用P和Q表示，在P端投入电容后，放电回路如图2所示。图中Z1和G1为线路的等效电阻和分布电感，G0和R0为用于故障定位分布电感和电容，故障点的过渡电阻为Zf。

图2 故障回路图Fig.2 Fault loop circuit

为确保电容放电电流为衰减振荡形式，改变G0和R0大小，使图2电路满足则需对二阶电路进行微分求解得到故障位置处配电线路P端放电电流I1。

式中：λ1为振荡频率；β1为衰减系数；U0为发生故障高压电力电缆配电线路两端电压。λ1和β1表达式分别为：

由于式（7）放电电流I1是Prony 级数中的一项，因此可采用一阶Prony 分解法获取放电电流的振荡频率和衰减系数[8]。

联立式（8）和式（9），则有：

同理在该高压电力电缆配电线故障位置处线路Q端投入电容，可以得到：

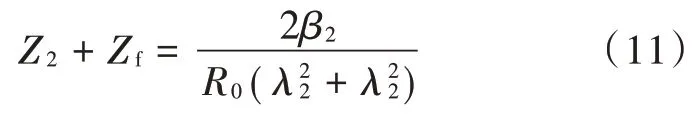
用式（10）减去式（11）得到：

但在该高压电力电缆配电线路中Z1与Z2之和一定，代表该配电线路的总电阻[9]，存在：

式中：d表示该配电线路的全长；单位距离配电线路长度代表的电阻值用Zunit表示。可采用式（12）和式（13）求得高压电力电缆配电线路故障位置线路两端的电阻Z1和Z2，更加精确地检测出线路故障信息[10]。

2 实验分析

实验为验证本文方法应用在高压电力电缆配电线路在线故障检测的高效性，以一段长300 km 的高压电力电缆配电线路为例，进行故障在线检测，仿真分析本文方法的高压电力电缆配电线路故障在线检测结果。将本文方法与基于VMD 和TEO 的高压电力电缆配电线路故障在线检测方法检测结果进行对比，结果分别如表1和表2所示。

表1 本文方法配电线路故障在线检测结果Table 1 Distribution line fault online detection results obtained by the presented method

分析表1数据结果可以看出，本文方法在线检测高压电力电缆配电线路故障发生距P点距离与故障实际距P点的距离绝对误差较小，故障检测距离绝对误差最大和最小分别为3.88 km 和0.14 km，平均值为1.50 km；故障检测距离绝对误差率变化区间为0.005～0.016，平均误差率为0.009 5。结果表明本文方法能精确检测高压电力电缆配电线路故障发生位置，具有较高的在线故障检测精度。

同样分析表2数据结果可以看出，基于VMD 和TEO 配电线路故障结果精度较差。该方法故障检测距离绝对误差和绝对误差率平均值分别为22.78 km 和0.157 4，高于本文方法的15 倍和17 倍。对比结果表明，本文方法用于在线检测高压电力电缆配电线路故障中有较强的应用价值。

高压电力电缆配电线路故障在线检测时，可能会发生错误故障检测（非线路故障视为线路故障或线路故障视为非线路故障）和遗漏故障检测，经过多次实验，得到两种方法不同实验次数下错误故障检测率和遗漏故障检测率分别如图3和图4所示。

表2 基于VMD 和TEO 的配电线路故障在线检测结果Table 2 Results of distribution line fault online detection based on VMD and TEO

图3 错误故障检测率Fig.3 Error rate of fault detection

图4 遗漏故障检测率Fig.4 Omission rate of fault detection

从图3可看出，本文方法在线检测高压电力电缆配电线路的错误故障检测率始终较低，其变化范围为3.55%～6.12%，平均错误故障检测率仅为4.78%；而基于VMD 和TEO 故障检测方法整体平均错误故障检测率为17.52%。结果表明本文方法的高压电力电缆配电线路错误故障检测率低，可准确分辨线路故障和非线路故障。

从图4可知，本文方法在线检测高压电力电缆配电线路的遗漏故障检测率曲线变化幅度不明显，平均遗漏故障检测率为2.41%；基于VMD 和TEO 故障检测方法平均遗漏故障检测率为21.29%。说明本文方法能较全面地在线检测高压电力电缆配电线路的故障，提升高压电力电缆配电线路的供电效果。

3 结 论

高压电力电缆配电线路具有较多优势，在配电系统中应用较强。本文先根据行波故障测距原理，检测已知行波速度和未知行波速度时高压电力电缆配电线路故障位置，通过引入故障回路振荡频率和衰减系数，将电容安装在发生故障位置线路两端，降低配电线路电感对故障在线检测的影响，精确了在线检测高压电力电缆配电故障线路的两端电容。