基于偶极子格网法ASE分析的工程应用
2019-09-23黄勇强
张 欢,刘 欣,黄勇强,桑 岚
(航空工业洪都,江西 南昌,330024)
0 引言
现代飞机的设计采用电传飞行控制系统以提高飞机的操纵性、稳定性及机动性,为飞机提供良好的飞行品质。然而,由于飞机的非定常气动力,飞行控制系统以及飞机结构动力(弹性力、惯性力)之间的耦合,可能破坏飞机原有的气动弹性平衡,以至产生不稳定现象。美国的 YF-16、YF-17、F-18、X-29 飞机在早期飞行试验中曾经遇到过这种气动伺服弹性不稳定现象。以YF-16为例,YF-16飞机在首飞前进行过大量常规的计算和试验工作,没有发现不稳定现象。但是在第8、9、10次飞行中,飞机出现强烈振动,飞行员感觉这种振动表现为翼尖导弹的俯仰运动。经过分析,这是一种气动伺服弹性不稳定现象,是由翼尖导弹俯仰模态与控制系统横滚回路耦合引起的。对飞机进行气动伺服弹性(ASE)稳定性分析和研究,已成为当今飞机开发研制过程中必不可少的新课题,越来越引起飞机设计师的重视[1]。
本文根据现代飞机的特点,结合工程实践需求进行了气动伺服弹性稳定性的理论分析,并构建了计算和试验为一体的飞机气动伺服弹性稳定性检查系统,在工程上得到应用和验证。
1 气动伺服弹性稳定性分析方法
1.1 气动弹性运动方程
弹性飞机气动弹性运动方程一般可以写为
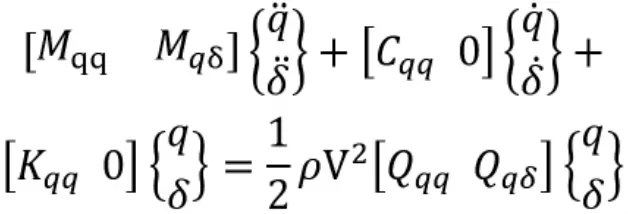
其中,q为飞机机体模态坐标向量,δ为控制面刚体偏转坐标向量,ρ为大气密度,V为飞行速度,Mqq和Mqδ为广义质量矩阵,Cqq为广义阻尼矩阵,Kqq为广义刚度矩阵,Qqq和Qqδ为广义非定常气动系数矩阵。
1.1.1 广义质量矩阵
飞机有限元模型的结构质量矩阵记为Ms,它是一个n×n阶的矩阵,则有广义质量矩阵计算公式

这里,Mqq和Mqδ分别为m×m和m×3阶的矩阵。
1.1.2 广义刚度矩阵
广义刚度矩阵Kqq为对角阵,有以下形式

其中,Wi为各阶机体模态的固有频率。
1.1.3 广义阻尼矩阵
广义阻尼矩阵Cqq也为对角阵,有以下形式

其中,ξi为各阶机体模态的阻尼比。
1.2 非定常气动力计算
非定常气动力是气动弹性分析的基本原始数据之一。非定常气动力的计算需要考虑谐振荡和非谐振荡两种形式。非谐振荡计算相当复杂,现在发展起来的用于工程计算的绝大多数都是谐振荡的非定常气动力计算。它有许多种计算方法,而其中基于小扰动方程速度势的用于计算非定常气动力的偶极子格网法,具有计算结果准确、计算时间短的优点。本文采用该方法进行非定常气动力计算。
根据非定常气动力理论,从网格控制点满足的积分方程可以得到

最终,可得广义非定常气动力的表达式

其中,弹性机体模态、控制面偏转模态对应的广义非定常气动力系数阵为

1.3 弹性机体传递函数
引入谐振荡运动条件q=exp(iwt)和 δ=exp(iwt),可得到频域气动弹性方程为

解此方程最后得到

其中,G=ΦFsA-1B为弹性机体传递函数矩阵,它为5×3阶的矩阵,具体有以下关系式。
1.4 闭环稳定性分析
弹性飞机机体与飞控系统增稳控制律构成的闭环系统如图1所示。若不考虑飞控系统中各个不同通道之间的耦合,整个飞机气动伺服弹性系统可以看成是纵向、横向和航向三个分别独立的单输入/单输出系统。各通道的开环传递函数为
纵向通道:Lz=-(Tny)*g11+Twx*g21
横向通道:Lx=-Twx*g32
航向通道:Ly=-Twy*g43+Tnz*g53
当频率w由0变到+∞时,开环传递函数在复平面上的轨迹称为开环乃氏曲线。Nyquist稳定性判据是根据开环乃氏曲线来判断闭环系统稳定性的一种准则。它可叙述为:反馈控制系统稳定的充分必要条件是开环乃氏曲线顺时针包围临界点(-1,0)的圈数R等于开环传递函数右半s平面极点数P,即R=P,否则闭环系统不稳定[2]。
2 工程应用
2.1 问题描述
某飞机设计之初,进行气动伺服弹性分析,结果如图2~图4所示。
根据Nyquist稳定性判据,可以得出各通道气动伺服弹性稳定性结果如表1。

表1各通道气动伺服弹性稳定性计算结果
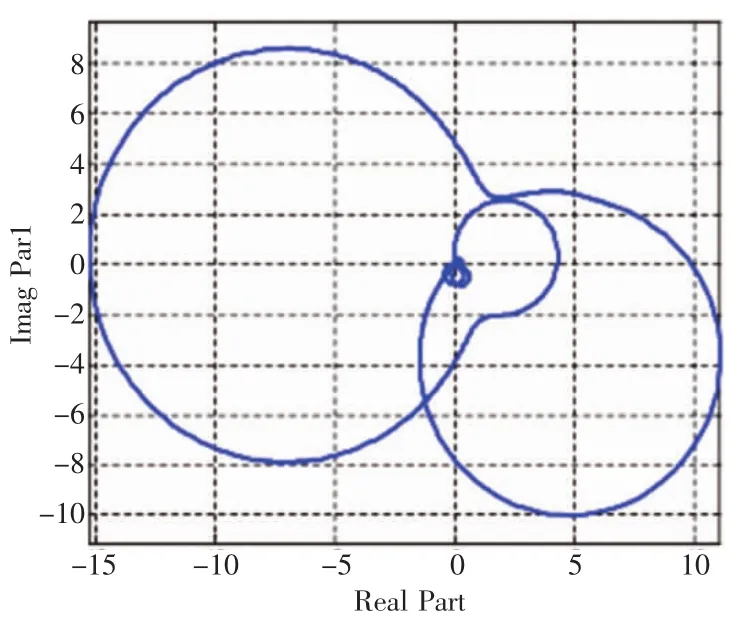
图2 纵向通道Nyquist图

图3横向通道Nyquist图
从计算结果可以看出,在该计算状态点,横向和航向通道是稳定的,但稳定裕度偏小;纵向通道则是不稳定的。
2.2 原因分析
2.2.1 气动面与模态选取的影响
为了考查气动面和模态选取的影响,对比了三种情况的气动伺服弹性计算结果:(a)全机气动面;(b)左右平尾气动面,10阶模态;(c)左右平尾气动面,第13和24阶模态。以上三种情况的Nyquist曲线如图5所示。
从图5可以看出:(a)与(b)情况的Nyquist曲线基本重合,说明在气动伺服弹性分析中,平尾气动力在全机气动力中占主要作用;(a)、(b)和(c)三种情况的Nyquist曲线在频率为19.4 Hz附近几乎重合,该频率对应的模态是第13阶模态(平尾对称一弯),这说明平尾对称一弯模态是引发纵向通道气动伺服弹性失稳的关键模态。
2.2.2 过载与角速度反馈的影响
为了考查各信号反馈回路对气动伺服弹性稳定性的影响,对比了以下两种情况:(a)同时具有法向过载和俯仰角速度反馈;(b)只有俯仰角速度反馈。这两种情况的Nyquist曲线如图6所示。
从图6可以看出,两种情况的Nyquist曲线重合得很好,这说明对于纵向通道的气动伺服弹性稳定性,法向加速度反馈的影响作用是很小的,俯仰角速率反馈回路占主要作用。
2.2.3 控制面广义耦合质量的影响
为了考查两种激励力的作用效果,对比了以下两种情况:(a)控制面的惯性力和气动力同时作用;(b)只有气动力作用。这两种情况的Nyquist曲线如图7所示。

图7控制面广义耦合质量对Nyquist曲线的影响
从图7可以看出,两种情况的Nyquist曲线相差很大。这说明,对于所分析的飞行状态点,控制面的气动力作用远比惯性力作用小,控制面广义耦合质量是使得开环传函幅值较大、导致气动伺服弹性闭环失稳的重要因素。
2.3 问题解决方案
飞机气动伺服弹性系统的稳定性受到多方面因素的影响,包括机体固有振动模态的频率与阻尼、控制面的质量分布、传感器的安装位置、作动器的动态特性以及增稳控制回路中的增益、滤波器特性等。
对于一架飞机,要提高其伺服气动弹性稳定裕度,理论上主要有以下三种办法:
1)改变飞控系统的传感器安装位置;
2)由于机身垂直一弯是一个敏感模态,可以通过调整机身结构进而改变机身垂直一弯的频率和节线来提高稳定裕度;
3)飞控系统调整结构陷幅滤波器参数,使其在谐振峰上的增益下降到可接受范围内。
对于第一个方案,虽然可以从根本上解决问题,但是由于传感器的布置方案是在飞机总体设计中就已经确定的,改变传感器安装位置可能会涉及到结构及飞机其他成品的布置,因此对于一个己经定型的飞机而言,改变其传感器的安装位置不太现实。
同样,对于第二个方法,由于机体结构已基本确定,对机体结构的调整难度极大,很难达到要求状态。
对于第三个方案,虽然调整飞控系统结构滤波器可能在一定程度上影响飞机的稳定储备和飞行品质,但如果选取合适的参数,可使对稳定储备和飞行品质的影响降低到可接受范围内。因此,为了解决飞机的伺服弹性稳定裕度不够的问题,决定在不影响飞控系统特性的基础上调整系统中的结构陷幅滤波器参数。
2.3.1 结构陷波器的确定
飞控系统纵向、横向和航向的结构陷波器的中心频率分别参考机身垂直一弯、机翼反对称一弯和机身侧向一弯进行设计,如表2所示。

表2结构陷波器模型
2.3.2 气动伺服弹性稳定性分析
将设计好的三个结构陷波器分别增加到纵向、横向和航向通道后,对纵向、横向和航向进行气动伺服弹性稳定性分析,结果如图8~图10所示。

图8纵向通道Nyquist图

图9横向通道Nyquist图

图10航向通道Nyquist图
从上述曲线可以看出,更改结构陷波器后,三个通道幅值裕度均大于6db,相位裕度均大于60°,满足国军标要求。
2.4 试验验证
结构模态耦合试验的目的是检查零空速条件下飞机——飞控系统的伺服弹性幅值稳定裕度及相位稳定裕度是否满足GJB 2191要求。
将试验状态点与气动伺服弹性理论分析的曲线进行对比,如图11~图13所示。

图11纵向通道理论曲线与试验对比图

图12横向通道理论曲线与试验对比图

图13航向通道理论曲线与试验对比图
从上述曲线可以看出,理论计算的曲线和试验曲线在趋势上基本一致,且谐振峰值所处频率相差不大。由此,可以认为理论分析具有一定的可信度,能够反映飞机的真实情况。但由于试验过程中不可避免的有噪音污染,导致试验曲线存在一定的跳点和误差。而理论建模略去了结构阻尼;有限源简化过程也存在误差;传感器、舵机模型建模与实物也存在偏差。这些都导致了理论计算和试验存在一定偏差。
3 结语
气动伺服弹性稳定性分析是飞机研制过程中的一项重要工作,其结果被作为飞机的放飞标准。本文以一工程实例介绍了气动伺服弹性分析技术在飞机设计中的应用,通过与试验对比表明该分析技术的可行性。然而理论分析结果的可靠性,取决于数学模型的精度。后续还需用试验数据修正理论分析的数学模型,从而得出更准确的分析结论。
