基于磁梯度张量不变量的椭圆误差消除方法*

袁 鹏,祗会强,靳 鸿,段晓倩,孙赫轩

(中北大学仪器科学与动态测试教育部重点实验室,太原 030051)

磁异常探测技术是未知爆炸物探测的重要手段,具有极高的军事意义和民用价值[1-2]。磁探测初始阶段测量磁场总量,后来又测量磁场分量和梯度,到现在发展到测量磁梯度张量。磁梯度张量测量技术和传统的磁场测量相比有巨大的优势,它的最大优点是能够有效的克服地磁场的影响,提高磁性目标的定位准确度,不足之处就是搭载平台对其定位结果的影响较大。

磁梯度张量不变量是由磁梯度张量通过某些变换获得的标量,这些标量不随坐标系的变化而变化,它适合于机动平台对磁性目标的定位,目前已经成为国内外的研究热点[3-5]。

磁梯度张量不变量定位方法,由于椭圆系数的存在,导致求解单位距离矢量和距离矢量模的过程中都存在一定的误差,单位距离矢量是测量点指向磁源的单位方向矢量,距离矢量模是测量点到磁源的距离。针对该问题,提出了一种利用磁梯度张量不变量消除椭圆误差的改进定位方法。该方法利用单位定位矢量和定位矢量的模相乘,来求出定位矢量,本文的创新点是:①提出一种新的单位定位矢量计算方法,该方法主要利用测量点和磁性目标形成的距离矢量与磁梯度张量矩阵的绝对值最小的特征值对应的特征向量的垂直关系。②提出一种距离矢量模的修正方法,该方法利用磁梯度张量的特征值不变量来消除椭圆系数,从而修正定位矢量的模。

本文所提出的基于磁梯度张量不变量的改进定位方法,可以有效地避免地球磁场的影响,实现隐蔽磁性目标的定位,而且适用于移动平台,有很高的应用价值。

1 磁梯度张量不变量定位方法

当探测距离大于2.5倍磁性目标自身长度时,磁性目标就可以看作一个磁偶极子[6-7]。距磁偶极子r处的磁场大小可以表示成

(1)

式中:μ0是真空磁导率;M是磁性目标的磁矩;r是测量点到磁性目标的距离;r0是沿r方向的单位方向向量。磁梯度张量表示磁场三分量在3个方向的空间变化率,由9个元素组成,其表达式为

(2)

式中:G为磁梯度张量。磁性目标在其周围产生的磁场我们将它看作静磁场,由麦克斯韦方程组可知,B的旋度和散度都为0,所以G是对称矩阵,只需要计算G的5个元素。定义CT=|G|,在磁偶极子模型场源条件下其表达式为

(3)

式中:参数k是在空间中为非球面分布的常数,在定位矢量正交于磁矩的方向上取得最小值,在定位矢量平行于磁矩的方向上取得最大值。CT的等值线是以磁源为中心的近似椭圆[8]。

地球磁场约为5万nT,分量有几千到几万nT,但地磁场的梯度[9-10]小于等于0.02 nT/m,所以测量磁梯度张量可以消除地磁场的干扰。

磁梯度张量系统的测量阵列采用正六面体结构,如图1所示,坐标原点位于正六面体的中心,三个坐标轴分别垂直穿过对应正六面体的三个平面的中心点,8个磁传感器分别位于正六面体的8个顶点,传感器的三轴与坐标系的三轴方向保持一致。正六面体每个平面内都有4个传感器,可以测得六个面中心的磁梯度张量,以Z轴正方向的平面为例:

图1 张量系统测量阵列

(4)

(5)

式(4)中G为磁梯度张量,式(5)中S为每个磁传感器测得的磁场3分量,d为正六面体测量阵列的边长。

由空间梯度定义可知,标量函数某一点的空间梯度指向函数在该点处空间变化率最大的方向。对测量阵列而言,其测量基点磁梯度张量的模空间梯度为

(6)

式中:i、j、k为正交坐标系的基向量,ΔCT,X为X方向的两个测量平面磁梯度张量的模的差值,即 ΔCT,X=CT,+X-CT,-X,其余两个方向同理.CT的方向由测量阵列基点指向磁性目标,将其单位化即可得到单位定位矢量:

(7)

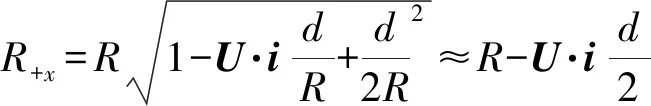
(8)

同理

(9)

(10)

联立式(8)和式(10)得

(11)

求出单位定位矢量和定位矢量的模,最终得到定位矢量为

(12)

2 椭圆误差消除方法

把Wiegert提出的STAR定位方法[11-12]称为原始方法,原始方法由于存在椭圆系数而有一定的误差。误差来源于式(3)中的椭圆系数k,k值的大小因为磁距与距离矢量方向的夹角的变化而变化,而原始方法把k看作一个不变的常数,所以造成了误差。由于椭圆系数k的变化造成的计算误差主要有三处:①式(6)对CT中的变量求导,其中有两个变量r和k,原始方法只对r进行求导,造成单位距离矢量的误差。②式(10)中正六面体的X轴正负方向平面的CT相除,原始方法把k看作一个常数,相互抵消,实际上两个不同点的k有微小差别,造成距离矢量模的误差。③式(11)求解定位矢量模R过程中,使用了式(6)计算得到的有误差的单位距离矢量,也会造成距离矢量模的误差.

通过上述分析可知,因为椭圆系数的存在,原始方法计算得到的单位距离矢量及距离矢量的模都存在误差。

2.1 新的单位距离矢量计算方法

本文提出了一种新的单位定位矢量计算方法,所提方法利用测量点和磁性目标形成的位置矢量与磁梯度张量矩阵绝对值最小的特征值对应的特征向量之间的垂直关系[13],这个垂直关系由磁梯度张量不变量推导得出。

该方法使用如图1所示的正六面体结构的测量阵列,坐标原点位于正六面体的中心,三个坐标轴分别垂直穿过对应正六面体的两个平面的中心点,测量阵列每个面都有4个三轴磁传感器,可以测出每个正六面体每个面中心处的磁梯度张量。

设X轴正方向平面中心的点是P1,P1点的磁梯度张量为G1,矩阵G1的特征值为λ1、λ2、λ3,且|λ1|>|λ3|,|λ2|>|λ3|,λ3对应的特征向量是V3,Y轴正方向平面中心的点是P2,P2点的磁梯度张量为G2。矩阵G2的特征值为λ4、λ5、λ6,且|λ4|>|λ6|,|λ5|>|λ6|,λ6对应的特征向量是V6,Z轴正方向平面中心的点是P3,P3点的磁梯度张量为G3。矩阵G3的特征值为λ7、λ8、λ9,且|λ7|>|λ9|,|λ8|>|λ9|,λ9对应的特征向量是V9。V3、V6和V9是正六面体3个面磁梯度张量矩阵绝对值最小的特征值对应的特征向量。

正六面体的中心O到磁性目标之间的位置矢量为r,P1点到磁性目标之间的位置矢量为r1,P2点到磁性目标之间的位置矢量为r2,P3点到磁性目标之间的位置矢量为r3,由磁梯度张量不变量推导出的垂直[13]关系可得

(13)

由O、P1、P2的位置关系,利用向量运算可以得到:

(14)

将式(14)中的等式代入式(13)可以得到

(15)

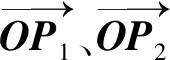
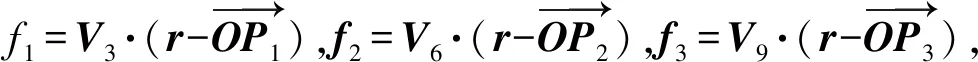
f=max(|f1|,|f2|,|f3|)

(16)

利用粒子群优化算法对式(16)中x,y和z进行优化,使得f最小,即可求解出x,y,z。

粒子群优化算法是一种启发式优化算法,它是从随机解出发,通过迭代来寻找最优解,通过适应度函数来判断解是否最优,通过追随当前最优解来寻找全局最优解。这种算法的优点是实现容易、精度高、收敛快,在解决实际问题的过程有巨大的优越性。所以单位距离矢量为

(17)

2.2 距离矢量模的修正方法

正六面体的X轴正负方向平面中心的椭圆系数k有微小的差别,所以两个平面中心点的椭圆系数分别设为k1,k2,联立式(3)、式(10)和式(17)可得

(18)

联立式(8)和式(17)得

(19)

由文献[14]可知椭圆系数的公式

(20)

由文献[13]可知磁梯度张量的特征值不变量公式

(21)

联立式(20)和式(21)得

(22)

所以有

(23)

将式(23)代入式(19)可以得到修正的距离矢量的模

(24)

求出单位距离矢量和距离矢量的模,得到修正后的距离矢量为

(25)

3 仿真实验分析

针对本文提出的椭圆误差修正方法,对可能造成误差的因素进行仿真,并分析仿真结果。仿真实验工具有MATLAB软件和COMSOL多物理场仿真软件。可能影响定位精度的因素有:①测量系统的基线d;②高斯噪声;③磁传感器的测量精度。

仿真时通过式(12)计算原始方法的距离矢量,通过式(25)计算改进方法的距离矢量。

仿真实验的初始条件:测量阵列是图1所示正六面体,以正六面体的中心为坐标原点建立笛卡尔坐标系,设磁源坐标为(10,20,30)单位m;磁性目标的磁矩m=(5 000 000,5 000 000,7 071 100)Am2;当地的地磁场真实值为(30 000,2 200,44 000)nT。

3.1 正六面体测量系统的基线

仿真方法:仿真时正六面体测量系统的基线d从0.1 m增加到2.2 m,其他量保持初始条件不变,加入地磁场.比较理论值与仿真结果,得出结论。

仿真结果如图2,图2横坐标表示正六面体基线d从0.1 m增加到2.2 m,图2纵坐标为测量点与理论位置的绝对误差,单位是m。三种线型的曲线表示三种传感器精度对应的仿真结果。

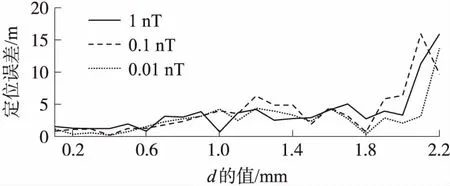
图2 测量系统基线d变化时的定位误差

从图2可知,正六面体基线d小于等于0.4 m时,定位误差较小,比较稳定,当d大于0.4 m时,系统的定位误差逐渐增大。

3.2 高斯噪声仿真实验

仿真方法:正六面体的基线d=0.4,测量系统仿真时,加入高斯噪声,噪声的信噪比从10增加到60,其他量保持初始条件不变,加入地磁场,每个信噪比都仿真100次,然后求解100次仿真结果的平均值。比较理论值与仿真结果,得出结论。

仿真结果如图3,图3横坐标表示高斯噪声的信噪比从10增加到60,图3纵坐标为100次仿真结果的平均值与理论位置的绝对误差,单位是m。三种线型的曲线表示三种传感器精度对应的仿真结果。

图3 高斯噪声信噪比变化时的定位误差

从图3可知,随着高斯噪声信噪比的增大,测量系统的定位误差迅速减小,当信噪比大于等于50时,定位误差达到最小并趋于稳定。

3.3 磁传感器的精度

仿真方法:正六面体的基线d=0.4,磁源沿一条直线运动,在不同传感器精度条件下,其他量保持初始条件不变,分别测量出对应磁源的坐标。具体方法是,磁源从坐标(10,20,0)沿Z轴正方向移动到(10,20,70),单位是m,每次移动2.5 m,选择1 nT、0.1 nT和0.01 nT三种传感器精度,在其他量保持初始条件不变的前提下,加入地磁场,分别测量这三种精度下每次磁源移动后的坐标。

仿真结果如图4,图4横坐标表示磁源的Z坐标从0增加到70,图4纵坐标为三种传感器精度测量的绝对误差,单位是m。三种线型的曲线表示三种传感器精度对应的仿真结果。

图4 传感器精度变化时的定位误差

在图2到图4中三种线型的曲线表示1 nT、0.1 nT和0.01 nT三种传感器精度对应的仿真结果,可以看出不论是在系统基线的仿真实验,还是高斯噪声实验中,还是在磁源直线运动的传感器精度实验中,都有以下结论:传感器精度越高,定位误差越小。

由图4还可以看出当传感器精度为1 nT,磁源在点(10,20,20)时,测量误差开始增大;当传感器精度为0.1 nT,磁源在点(10,20,30)时,测量误差开始增大;当传感器精度为0.01 nT,磁源在点(10,20,55)时,测量误差开始增大;由此可以得出以下结论:本文所提改进定位方法,传感器精度为1 nT时的测量半径是30 m,传感器精度为0.1 nT时的测量半径是37 m,传感器精度为0.01 nT时的测量半径是60 m左右。

3.4 磁源的圆形轨迹运动验证实验

为了测试系统的整体性能,本文进行了磁源圆形轨迹运动定位实验。在加入地磁场基础上,正六面体的基线d=0.4,噪声的信噪比为50,传感器精度为0.1 nT,磁源沿圆的轨迹移动,使用原始方法和本文所提改进方法分别对磁源进行定位,观察定位结果,分析两种定位方法的轨迹,得出结论。

正六面体测量阵列以正六面体的中心为坐标原点建立笛卡尔坐标系。在地磁场和高斯噪声环境下,其他量保持初始条件不变,磁源沿圆的轨迹从初始位置(10,20,30)绕Z轴逆时针旋转一周,每次旋转10°,共旋转36次,每次磁源位置更新后,分别使用原始方法和本文所提改进方法分别对磁源位置进行定位,记录定位结果。

仿真结果如图5、图6和图7,三个图中的实线是圆形轨迹的理论值。

图5 磁源圆形轨迹运动原始方法横纵坐标仿真图

图6 磁源圆形轨迹运动改进方法横纵坐标仿真图

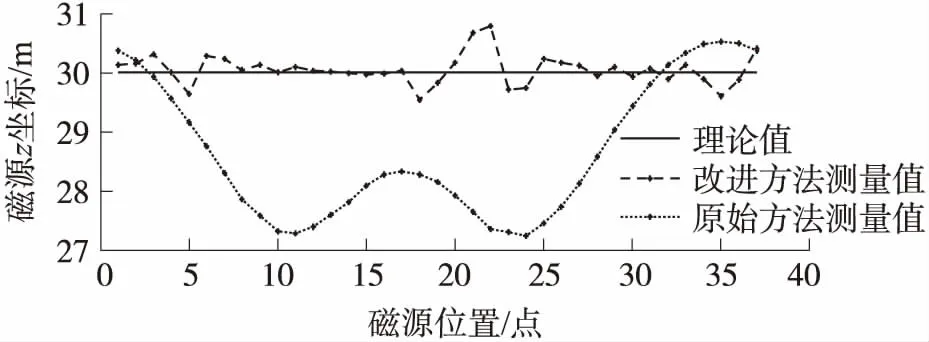
图7 磁源圆形轨迹运动两种方法z坐标坐标仿真图

图5中的虚线是使用原始方法测量出的磁源轨迹横纵坐标,图6中的虚线是使用本文所提改进方法测量出的磁源轨迹横纵坐标,图5和图6的横坐标都是磁源轨迹的横坐标,单位是m,图5和图6的纵坐标都是磁源轨迹的纵坐标,单位是m,图7中的点线是使用原始方法测量出的磁源轨迹z坐标,图7中的虚线是使用本文所提改进方法测量出的磁源轨迹z坐标,图7的横坐标表示磁源的第n次旋转,图7的纵坐标表示两种方法测量出的磁源轨迹z坐标,单位是m。

从图5～图7可知,在磁源的圆形轨迹运动定位实验中,本文所提改进定位方法在x,y和z轴的误差都在1 m以内,相对于原始方法的误差有很大程度的减小,定位精度大幅度提高。

4 总结

本文针对现有的磁梯度张量不变量定位算法存在椭圆误差的问题,提出了一种利用磁梯度张量不变量消除椭圆误差的改进定位方法。根据仿真实验的结果可得,本文所提的改进方法消除了椭圆误差,定位误差相比于原始方法有大幅度的减小,可以实现地磁环境和一定信噪比的高斯噪声情况下的实时精确定位,而且该方法适用于移动平台。在改进方法中,测量系统的基线d=0.4 m时,可以取得较小的定位误差;信噪比大于50的高斯噪声对测量系统的影响较小;传感器的精度越高,定位误差越小。所以本文所提的改进方法有很好的定位效果,不足的地方就是对传感器的精度要求较高。