PROBABILITY INEQUALITIES AND ROSENTHAL INEQUALITIES FOR THE SEQUENCE OF MARTINGALE DIFFERENCES
2019-09-21XUMingzhouCHENGKunDINGYunzhengZHOUYongzheng
XU Ming-zhou, CHENG Kun, DING Yun-zheng, ZHOU Yong-zheng
(School of Information Engineering, Jingdezhen Ceramic Institute, Jingdezhen 333403, China)
Abstract: In this paper, we discuss some inequalities for the sequence of martingale differences. By using properties of conditional expectation and elementary inequalities, we obtain the basic inequalities of Bernstein, Kolomogrov, Hoeffding for the sequence of martingale differences,which extend the results on the case of bounded random vectors. Moreover, we obtain classical Kolmogorov and Rosenthal inequalities for maximum partial sums of martingale differences, which complement the results on the case of independent and negatively dependent random variables under sub-linear expectations.
Keywords: martingale differences; Bernstein inequality; Kolmogorov inequality; Hoeffding inequality; Rosenthal inequality
1 Introduction and Main Results
To prove limit theorems in probability theory such as laws of large numbers, central limit theorem, etc., one need to use necessary probability inequalities, which attract attentions of many authors. Ahmad and Amezziane[1]proved extensions of the basic inequalities of Bernstein, Kolmogorov and Hoeffding for the sums of bounded random vectors. Li [2]established Bernstein inequality of the sequence of the martingale differences. Bercu and Touati [3] proved several exponential inequalities for self-normalized martingale by introducing a new notion of random variable heavy on left or right. Fan et al. [4] obtained exponential inequalities of Bennett Freedman, de la Pe˜na, Pinelis and van de Geer. Fan et al. [5] proved martingale inequalities of type Dzhaparidze and van Zanten. Zhang obtained Rosenthal inequalities for independent and negatively dependent random variables under sub-linear expectations. Xu and Miao [6] proved almost sure convergence of weighted sums for martingale differences. Yu [7] obtained complete convergence of weighted sums for martingale differences. Wang and Hu [8] established complete convergence and complete moment convergence for martingale difference sequence. It is natural to ask whether or not the basic inequalities of Bernstein, Kolmogorov and Hoeffding, and Rosenthal inequalities for the sequence of the martingale differences hold. Here we give an affirmative answer to this problem. We state the main results in this section, and present the proofs in Section 2.
Let{ξi,Fi,i ≥1}be martingale differences on the probability space(Ω,F,P)such that, i = 1,2,···, where B is nonrandom. Set= inf{c > 0,P(|ξ| ≤c) = 1},which is called the essential supremum of random variable ξ. Denotei ≥1, where F0= {∅,Ω}. Let a1,··· ,anbe positive real numbers such thatandWrite. The following are the main results.
Theorem 1.1(i) For any x>0,
(ii) For any x>0, P(Sn≥x)≤exp
(iii) For any x>0, P(Sn≥x)≤
Remark 1.1(i), (ii), and (iii) in Theorem 1.1 is called to be Bernstein inequality,Kolmogorov inequality, and Hoeffding inequality, respectively. As pointed out in Fan et al.[5], in Theorem 1.1 Bernstein inequality (i) is implied by Hoeffding inequality (iii).
Theorem 1.2(Kolmogorov inequality)In particular,
Theorem 1.3(Rosenthal inequality) (a)

and

In particular,

(b)

In particular
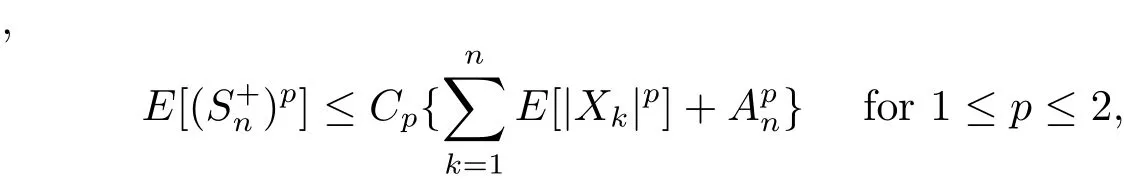
here Cpis a positive constant depending only on p.
2 The Proof of Main Results
Proof of Theorem 1.1For any α>0, by Chebyshev inequality, we obtain

As in the proof of Ahmad and Amezziane [1], Li [2], to prove the result in the theorem, we first obtain an upper bound for E(exp(αSn) for all α>0 and then choose α that the upper bound is minimized. The ideas originally come from Bernstein, Kolmogoroff, Hoeffding [9],Bennett [10]. Here the ideas also come from Bentkus [11], Ahmad and Amezziane [1], Li [2],and Gao and Wu [12].
(i) For any real z, the power expansion of exp(z) is


By the properties of conditional expectations, for<1, we get

Substituting (2.4) to (2.1), we obtain

We choose

the above inequality becomes


where

Therefore

Hence by the properties of conditional expectations, we have

Because 1+t ≤exp(t) when t>0, the right hand side above is bounded by

Substituting (2.6) into (2.1), we obtain

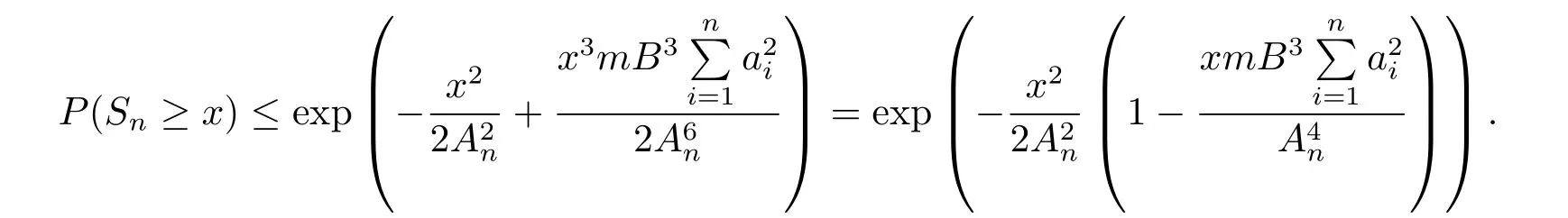
(iii) Note that exp(x)≤1+x+cx2if and only if c ≥(exp(x)−1 −x)/x2, we obtain

where c is a bound on
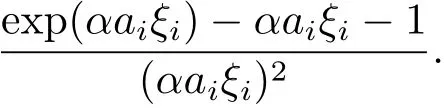
Because (exp(x)−1 −x)/x2is increasing in x and αaiξi≤αmB, we set

By the properties of conditional expectations, the above inequality becomes

Hence

Substituting (2.7) into (2.1), we obt ain
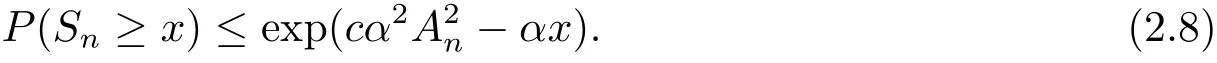

The ideas of the proofs of Theorem 1.2, Theorem 1.3 come from that of Zhang [13].
Proof of Theorem 1.2It follows that

Proof of Theorem 1.3(a) Let Tkbe defined as in the proof of Theorem 1.2. We first prove (1.1). Substituting x=Xn+1−kand y =to the following elementary inequality

yields

by the property of martingale differences. Hence

So (1.1) is proved.
For (1.2), by the following elementary inequality

we have

It follows that

Therefore by Hölder inequality

From the above inequalities, we obtain

(1.2) is proved.
(b) From (2.9) it follows that
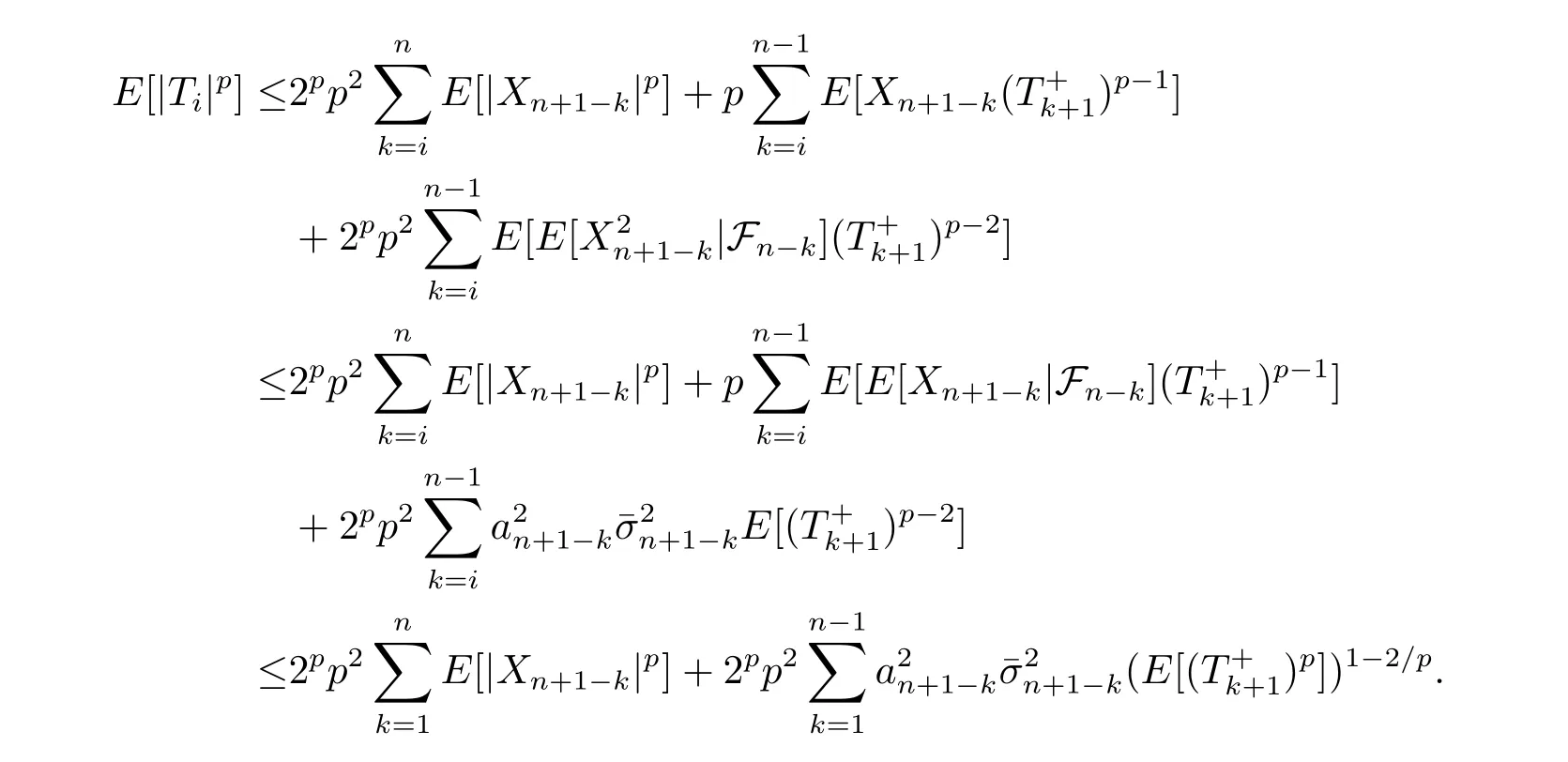
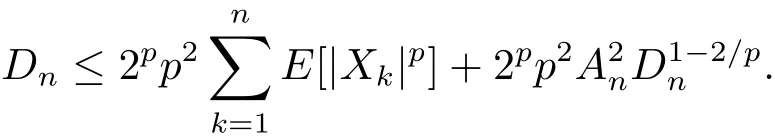
By the above inequality, we see that

(1.4) is proved.
杂志排行
数学杂志的其它文章
- MULTIPLICITY OF POSITIVE SOLUTIONS FOR QUASI-LINEAR ELLIPTIC EQUATIONS INVOLVING CONCAVE-CONVEX NONLINEARITY AND SOBOLEV-HARDY TERM
- A 2-DIMENSIONAL ANALOGUE OF S´ARKöZY’S THEOREM IN FUNCTION FIELDS
- LAZY 2-COCYCLE ON RADFORD BIPRODUCT HOM-HOPF ALGEBRA
- AN ESTIMATE FOR MAXIMAL BOCHNER-RIESZ MEANS ON MUSIELAK-ORLICZ HARDY SPACES
- 非一致分布下的在线分位数回归算法
- 扩张的圈Schrödinger-Virasoro 代数的二上同调群
