H对Mg2Si力学性能影响的第一性原理研究*

2019-09-21付正鸿李婷单美乐郭糠苟国庆

物理学报 2019年17期

付正鸿李婷单美乐郭糠苟国庆

(西南交通大学,先进材料教育部重点实验室,成都 610031)

1 引言

Mg2Si金属间化合物是Al-Mg-Si系铝合金主要的热处理强化相,高弹性模量、高硬度的Mg2Si颗粒弥散分布于铝合金基体中,通过阻碍位错运动在Al-Mg-Si系铝合金形成弥散强化作用,使铝合金强度硬度大幅度提高[1,2].由于Mg2Si的高熔点(1085 ℃)[3],被用于替代SiC陶瓷制备铝基复合材料,且具有良好的切削加工性和成形性.因此,Mg2Si金属间化合物的研究备受关注[4].

对于Mg2Si金属间化合物的理论研究,主要采用基于密度泛函数理论的第一性原理计算方法.任玉艳等[5]对Mg2Si金属间化合物的结构稳定性、热力学和力学性能进行了系统的第一性原理计算研究,理论计算值与实验值十分接近.余本海等[6]采用第一性原理的方法对Mg2Si的同质异相体的晶体结构、电子结构及弹性性质进行了全面研究.

氢由于其原子半径极小,容易在材料中扩散,并引起材料性能的变化.氢原子对晶体结构和力学性质影响的第一性原理计算已经成为目前研究的热点.韩秀丽等[7]采用第一性原理的方法对Ti-H体系的晶体结构和能量进行了研究,氢原子的加入引起Ti晶体的晶格畸变,降低了晶体的结合能.氢在α-Fe和γ-Fe中掺杂均使晶体结构产生不同程度的畸变,并降低了材料的塑性[8,9].姚宝殿等[10]的研究显示氢对Ti3SiC2的力学性质影响不大.对α-Ti-H键重叠集居数的研究发现[11],氢减弱了近邻原子间的成键强度,存在弱键效应; 而在β-Ti-H中,氢增加了近邻钛原子间的键重叠集居数,存在强键效应.氢的加入也会使Nb晶体发生类似的电子结构变化[12].α-Fe2O3-H中,H和O之间成键,费米面附近出现了新的杂化能级,价带顶变宽,同时带隙由于导带底下移而减小,表明氢可以用来调节能带结构[13].

本文采用基于密度泛函数理论的第一性原理方法,构建Mg2Si-H体系,研究了氢原子浓度变化对Mg2Si金属间化合物弹性性质的影响,并对其力学性能的变化进行了深入分析.

2 计算方法

Mg2Si金属间化合物具有反萤石结构,空间群号为Fm3m(No.255),为面心立方 (FCC)结构,晶格常数a=b=c=0.676 nm,α=β=γ=90°[14].Si原子占据顶角和面心位置,Mg原子位于Si原子组成的四面体间隙中形成边长为0.5a的简单立方结构,余留体心位置的八面体间隙,成为H等小半径原子优先固溶位置.

本文采用基于密度泛函数理论(DFT)和平面波赝势的CASTEP(Cambridge sequential total energy package)模块,对不同H原子浓度的Mg2Si-H体系进行模拟计算.首先构建Mg2Si晶胞,几何优化后构建1×1×1,1×1×2,1×2×2的Mg2Si超晶胞,在体心八面体间隙中掺杂H原子,形成H原子掺杂浓度分别为7.69 at.%,4 at.%和2.05 at.%的Mg2Si-H体系,如图1所示.对掺杂H原子后的超晶胞再进行几何优化,得到稳定的Mg2Si-H体系,然后对Mg2Si-H体系进行弹性性质计算.为更直观地反映H原子掺杂对Mg2Si力学性的影响,分别计算了1×1×2的Mg2Si超晶胞和1×1×2的Mg2Si-H (4 at.%)超晶胞沿[001]方向进行拉伸的应力-应变曲线.拉伸应变通过改变晶胞[001]方向的尺寸进行施加,几何优化后获得对应的应力值.

计算过程采用周期性边界条件,结构优化和弹性性质计算过程中,采用广义梯度近似(genaral gradient approximation,GGA)中的质子平衡方程(proton balance equation,PEB)来处理电子间的交互关联能,势函数选用倒异空间中表述的超软赝势(ultrasoft pseudopotential).计算中平面波截断能量(cut off energy)取400 eV,最大内应力为1×10-3GPa,原子最大位移为2×10-4nm,能量收敛标准为1×10-6eV/atom.第一布里渊区k-point矢量分别取9×9×9,9×9×4和9×4×4.

图1 H原子位于八面体间隙的Mg2Si-H体系超晶胞结构模型Fig.1.Super-cell structural model of Mg2Si-H system.

在三向应力下,材料共有36个弹性常数Cij(i=1-6,j=1-6).Mg2Si晶体为立方结构,因此存在三个独立的弹性常数,即C11,C12和C44,分别体现体系在[100],[111]和[011]三个方向的抗变形能力.当C11,C12和C44同时满足C11-C12＞ 0,C11＞ 0,C44＞ 0和C11+2C12＞ 0四个条件时,合金体系才可以稳定存在,满足力学性能稳定性条件[15].立方晶系剪切模量C'可由C11和C12计算:

材料的力学性质在微观上可以通过弹性常数、体模量、杨氏模量、剪切模量、泊松比和体模量/剪切模量之比等体现.多晶弹性模量通常可由单晶弹性常数计算获得,计算方法可用Voigt模型和Reuss模型描述.经验证,Voigt模型和Reuss模型所得模量通常为多晶模量的上限和下限,因此Hill[16,17]对两者进行数学平均,发现所得值与实测值一致性更好.因此,实际应用中Hill模型更为常用.因此本文中Mg2Si体模量BH,剪切模量GH和杨氏模量E的计算如下:

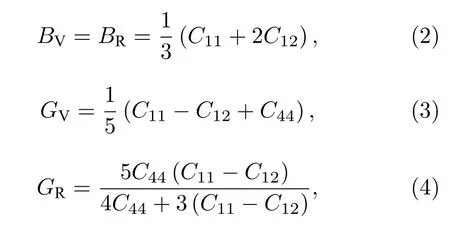
其中BV和GV分别为Voigt模型的体积模量和剪切模量,BR和GR分别为 Reuss模型的体积模量和剪切模量.Hill模型中体积模量B和剪切模量G分别为:

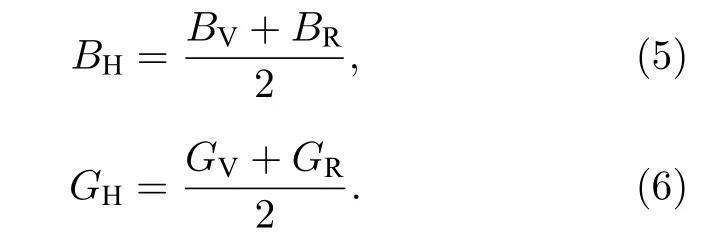
杨氏模量E和泊松比ν可由B和G计算得到[18,19]:

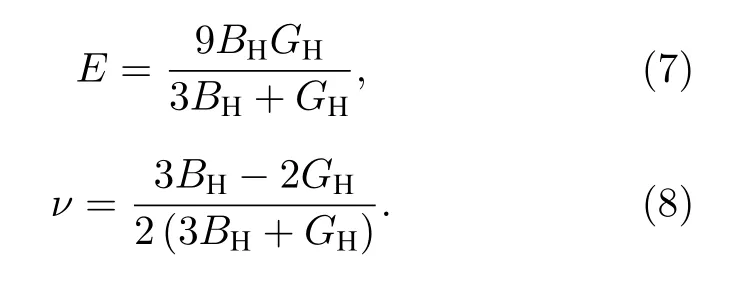
通常情况下,B反映材料抗体积压缩能力;G反映材料抗剪切应变的能力,且与硬度相关[19];E反映材料抗正应变的能力,也反映材料的硬度,E越大,材料的硬度越高[20].剪切应力下,ν越小则稳定性越好.B与G的比值是材料工程应用中必须考虑的重要参数,能反映材料的脆韧性,以1.75作为临界值.当B/G＞ 1.75时材料呈韧性,否则呈脆性[20,21].

材料的硬度与剪切模量、体模量之间存在直接的对应关系[22,23].Miao等[24]在通过第一性原理研究材料的力学性质中,提出了硬度H与杨氏模量E和泊松比ν之间计算的经验公式:

3 计算结果与分析

3.1 晶体弹性常数

Mg2Si-H体系晶体弹性常数C11,C12,C44和C'计算结果如表1所列.从表1中可以看出,所有体系中C11,C12和C44均同时满足C11-C12＞ 0,C11＞ 0,C44＞ 0和C11+2C12＞ 0四个条件,说明本文所建立的Mg2Si-H体系可以稳定存在,满足力学性能稳定性条件[15].本工作中的Mg2Si的弹性常数C11,C12和C44计算值分别为113.2,22.2和45.2 GPa,与其他学者的理论计算结果[6,20]相比,最大计算误差分别为1.15%,2.70%和0.88%,计算精度较高; 与其他学者的试验结果[21]相比,本工作中的,C12和C44的最大计算误差分别为10.16%,14.61和6.80%,说明本文计算方法具有较高的可靠性.

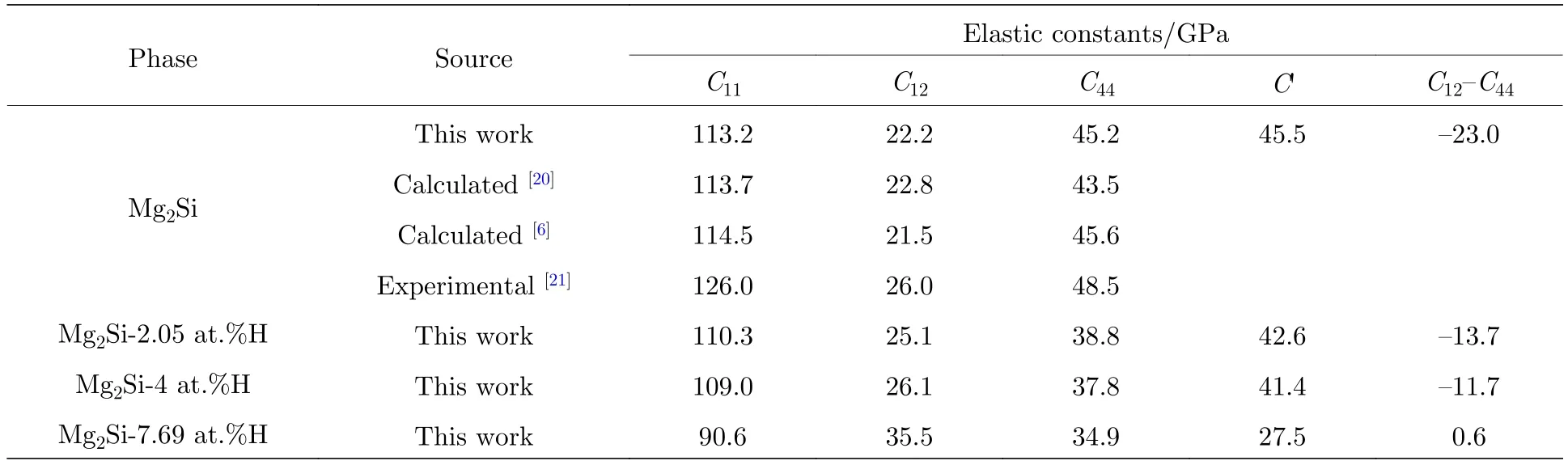
表1 Mg2Si-H体系晶体弹常数计算结果Table 1.Elastic constant of Mg2Si-H system.

图2给出了弹性常数C11,C12,C44和C'随氢原子浓度增加的变化趋势.C11值反映了体系在[100]方向的抗变形能力.从图2中可以看出,随氢原子浓度从0增加到7.69 at.%过程中,C11从113.2 GPa逐步减小到90.6 GPa,降低了20%,说明H原子的引入显著降低了Mg2Si在[100]方向抵抗变形的能力.C12反映了体系[111]方向的抗变形能力.从图2中可看出,H原子浓度从0增加到7.69 at.%过程中,Mg2Si的C12值从22.2 GPa增加到35.5 GPa,增加了59.9%,说明氢原子的引入使得Mg2Si抵抗[111]方向的抗变形能力明显提高.C44反映了体系[011]方向的抗变形能力,随H原子浓度从0增加到7.69 at.%,Mg2Si的C44从45.2 MPa降低到34.9 GPa,降低了22.8%,说明Mg2Si在[011]方向抗变形能力随氢原子浓度的增加而有所降低.经(1)式计算得到的单晶体剪切模量C'则随着氢浓度从0增加到7.69 at.%,从45.5 GPa降低到27.5 GPa,降低了39.5%,说明H原子具有显著降低Mg2Si单晶体的抗剪切变形能力.此外,C12-C44值还可表征晶体的脆性,当C12-C44＞ 0时晶体为塑性,当C12-C44＜0晶体为脆性[17].从表1可以看出,当H原子浓度达到7.69 at.%时,C12-C44值从由负值增加到正值,Mg2Si晶体发生了由脆性向塑性的转变.

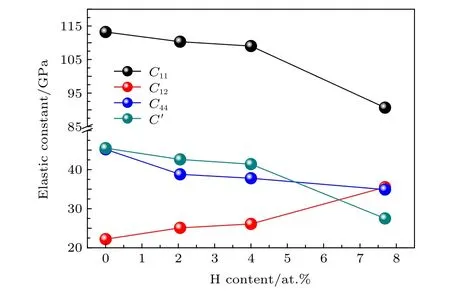
图2 弹性常数C11,C12,C44和C'随氢原子浓度增加的变化趋势Fig.2.Relationships between C11,C12,C44 and C' as a function of H atoms content.

3.2 多晶体弹性模量

经(5)-(9)式计算的剪切模量(GH)、体模量(BH)、弹性模量(E)、泊松比(ν)、脆性(BH/GH)及硬度(H)如表2所列.本工作中的GH,BH,E和ν值分别为45.3,52.5,105.6 GPa和0.16,与其他学者的理论计算结果[6,20]相比,本工作的最大计算误差分别为2.21%,1.73%,1.42%和4.29%,计算精度较高; 与其他学者试验结果[21]相比,本工作中的BH和E的最大计算误差分别为12.38%和13.63%,与试验结果同样十分接近,说明本文计算方法具有较高的可靠性.

图3给出了剪切模量(GH)、体模量(BH)、弹性模量(E)、泊松比(ν)、脆性(BH/GH)及硬度(H)随氢原子含量增加的变化趋势.弹性模量E是表征材料刚度的重要参数,E值越高,材料刚度越大.本工作计算结果表明,未引入氢原子时,Mg2Si的弹性模量E为105.6 GPa,随着体系内H原子浓度从0增加到7.69 at.%,弹性模量E逐步降低到79.5 GPa,降低了24.7%.切变模量G与弹性模量E类似,随着体系氢原子浓度从0增加到7.69 at.%,切变模量G从45.3 GPa降低到31.7 GPa,降低了30%.体模量B则随体系氢浓度的改变未表现出明显的变化.弹性模量E和切变模量G的大幅度降低,表明Mg2Si-H体系内氢原子浓度的增加,显著降低了材料的强度、硬度.与α-Ti相似[25],Mg2Si也表现出H致软化现象.硬度计算结果显示,体系的硬度从不含H原子时的10.31 GPa逐步降低到7.69 at.% H浓度时的4.55 GPa,降低了55.8%,印证了弹性模量E和切变模量G的计算结果.随着H原子浓度增加,体系硬度降低,B/G值逐步增加,泊松比ν也逐步增大.当H原子浓度达到7.69 at.%时,体系的泊松ν为0.28,与普通低合金钢基本相当[26].说明当大量H原子溶于Mg2Si时,Mg2Si将逐步失去其本身具有的高强度、高硬度和高脆性,可能严重降低以Mg2Si为增强相材料的强度.

3.3 拉伸性能

图4给出了1×1×2的Mg2Si超晶胞和1×1×2的Mg2Si-H(4 at.%)超晶胞沿[001]方向进行拉伸的应力-应变曲线.从图中可以看出,当Mg2Si中掺杂4 at.%的H原子时,其抗拉强度从15.21 GPa降低到14.12 GPa,延伸率则从0.3增加到0.36,说明H原子的掺杂使Mg2Si的强度降低,塑性增大.此外,掺杂4 at.% H原子的Mg2Si在弹性阶段的曲线斜率明显比不掺杂时要小,说明H原子的掺杂使Mg2Si的弹性模量降低.拉伸过程的应力-应变曲线结果与弹性模量计算结果得到很好地相互应证.

表2 Mg2Si-H体系模量Table 2.Modulus of Mg2Si-H system.

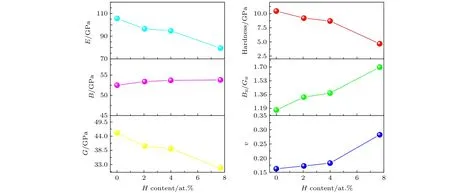
图3 剪切模量(GH)、体模量(BH)、弹性模量(E)、泊松比(ν)、脆性(BH/GH)及硬度(H)与体系H原子浓度的变化关系Fig.3.Shear moduli G,bulk moduli B,Young's moduli E,Poisson ratios ν,brittleness BH/GH and Hardness H as a function of H atoms content.

3.4 态密度分析

为探索H原子对Mg2Si力学性能影响微观机制,对体系的态密度和分波态密度进行了分析,如图5所示.图5(a)为Mg2Si晶体的电子态密度和分波态密度.由图可见,Mg2Si晶体的能带主要密集分布于费米能级两侧,具有典型的半导体特性.分波态密度显示,在-9--6 eV能量范围内,Mg2Si的态密度主要由Mg的3s和Si的3s态电子贡献,Si的3p态电子有少量贡献.在-5-0 eV能量范围内,Mg2Si的态密度主要由Mg的3p和Si的3s态电子贡献,Si的3p态电子有少量贡献.在0-20 eV能量范围内,Mg2Si的态密度主要由Si的3p和3s态电子贡献,Mg的3p态电子有少量贡献.当体系中引入7.79 at.%的H原子时,H原子显著增加了Mg和Si原子S和P态电子的贡献率,总态密度明显提高; 同时,体系在0-20 eV能量范围内的态密度峰缩减到0-6 eV范围内,变现为体系的禁带变窄,如图5(b)所示.于此同时,H原子的引入,还引起了费米能级处态密度的增加,态密度跨过费米能级区域.因此,H原子的引入使体系具有了一定的金属性质,从而引起材料强度、硬度的降低,韧性增加.