论如何在操作性学习之中培养学生的建模思想

薄文

摘 要 实际上，在小学时期的数学教学之中对数学模型这种思想加以运用，可以帮助儿童对所学知识进行深入理解、掌握以及灵活运用。操作性的学习乃是培养儿童建模思想的一个有效途径，儿童在操作性的数学活动之中可以对数学知识具体形成以及获得过程加以体验，进而构建相应的数学模型。本文以平行四边形的面积为例，对操作性的学习当中培养儿童建模思想的具体策略加以探究，希望能给实际教学提供相应参考。

关键词 小学数学;建模思想;平行四边形面积

中图分类号：G622         文献标识码：A       文章编号：1002-7661（2019）10-0171-01

如今新课标已经指出，数学教学需要把儿童已有的一些生活经验当作出发点，让儿童亲身历经把实际问题逐渐抽象成相应的数学模型，对数学模型进行理解以及应用的过程。数学建模乃是一种数学方面的核心素养，教师需通过相关操作性的学习活动来让儿童对数学知识具体行程以及获得过程加以体验，促使其建模意识以及能力得以提高，通过构建相应的数学模型对实际问题加以解决，发展儿童思维，并且提高其数学能力。

一、验证猜想，对数学模型进行感知

第一，猜想一下平行四边形面积与哪些因素有关。引导儿童猜想平行四边形面积和其底、高相关。

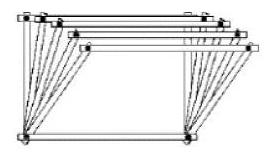
第二，拉动自制的矩形框架，让儿童对平行四边形面积和其底、高相关加以实际感受。

设计意图：通过拉动矩形框架，可以让儿童在实际操作之中对拉动期间平行四边形每条边长短一直不变，如果高变大，则面积变大，如果高变小，则面积变小这一事实加以直观感受，进而得到平行四边形面积和其底、高相关，和邻边没有关系。通过这个操作活动，可以抓住知识具有的生长点，对儿童学习起点加以把握，促使儿童对平行四边形的面积计算对应模型加以感知，激发其探究兴趣。

二、实践操作，建立数学模型

第一，让儿童通过小组合作进行动手操作，将平行四边形进行裁剪，并且拼成一个长方形。在此期间，数学教师可给各小组提供一对完全相同的平行四边形。

操作要求：（1）在两个图形的相同位置画出高线，同时标出高于底。（2）先让儿童进行组内交流讨论，只有再动手进行操作。（3）可以通过拼剪将平行四边形变成之前学过的一些图形。

第二，进行汇报交流。（1）沿着什么进行裁剪的？（2）通过拼剪将平行四边形变成了哪些图形？（3）平行四边形与转化之后所得图形具有什么关系？

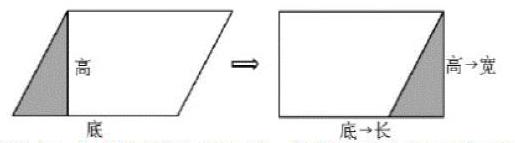
第三，按照长方形的面积公式把平行四边形的面积公式推导出来。

设计意图：通过动手操作，独立探索以及合作交流，儿童可以对所学知识加以深入理解以及掌握，促使其对由具体事物到抽象模型间的具体变化过程加以把握，引导其对建模思想加以领悟。进行小组操作期间，教师给儿童准备两个相同的平行四边形，对其中一个进行拼剪，这样便于儿童将拼剪之后所得图形和原图进行比较。儿童通过操作、对比可以体验平行四边形变为长方形的具体过程，这样可以培养儿童的空间观念，对数学思想加以有效渗透，帮助儿童得到平行四边形的面积公式。

三、问题解决，对数学模型加以运用

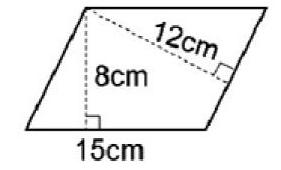
求出以下平行四边形面积：

设计意图：儿童经过一定的抽象提炼后，可初步建立起有关数学模型，之后教師可引导儿童在解决实际问题当中对数学模型加以运用，这样可以帮助儿童对数学模型进行深入了解，对其中包含的解题规律加以掌握。儿童在对数学模型加以应用期间，需要明确对平行四边形的面积加以计算期间，高于底必须对应，借助辨析增强平行四边形的面积公式这一模型。之后顺势引导儿童将高是12cm的对应底边长度求出来，这样可以提升儿童借助模型对问题进行解决这一能力。

四、回归本质，对数学模型进行丰富

教师可用细木条做一下长方形框，长方形框的长度是12cm，宽度是7cm，求其面积以及周长。假设将其拉成平行四边形，那么这个细木条围成的图形什么发生了变化，什么没有变化？说明理由。

第一，让儿童动手进行操作，找出其中的变量以及不变量。

第二，进行汇报交流。

设计意图：通过再次拉动这个长方形的木框，可以让儿童在实际操作之中对把长方形变为平行四边形的具体过程进行直观体验，让儿童感受在此过程之中，边长没有发生变化，所以周长不变。但是高度发生了变化，所以面积发生变化。这样一来，可以让儿童对所学知识进行深刻认识。

四、结论

综上可知，教学期间，数学教师对精心设计一些对儿童自主构建相应的数学模型有利的操作性的活动，以此来引导儿童有效、合理以及科学构建相应的数学模型。这样一来，可以让儿童对数学模型进行感知，通过实践操作，建立数学模型，并且对数学模型加以运用，帮助儿童对所学知识进行理解，同时培养儿童的建模能力以及建模素养。

参考文献：

[1]张晓伟.如何使学生在小学阶段构建数学建模思想[J].课程教育研究，2018（49）：141.