基于博弈论的大规模MIMO系统中导频分配方法

2019-09-20

测控技术 2019年3期

(西安电子科技大学综合业务网理论及关键技术国家重点实验室，陕西西安 710071)

近年来，大规模MIMO技术成为无线通信领域的一个研究热点[1]。大规模MIMO系统具有提高频谱效率和能量效率的优势，为了实现这些优势，目前仍然面临许多的挑战，其中之一便是导频污染问题。

由于导频数目有限，而用户数越来越多，邻近小区发送的导频信号很难完全正交，信道估计不可避免地要受到邻近小区中使用相同导频用户的干扰，然而，不准确的信道状态信息将会严重影响系统的性能。因此，如何减小导频污染对大规模MIMO系统性能的影响成为通信系统中亟待解决的问题。

就如何减小大规模MIMO系统中导频污染问题，大量的国内外文献已经进行了相关研究报道。文献[2]提出一种动态导频分配方案，根据目标小区用户和干扰小区用户之间的信号干扰强度差把干扰小区分为两类，优先对干扰强度差小的用户进行导频分配，并利用额外正交导频对所提方案进行了优化，该方案有效地提升了系统的下行平均可达和速率，但是该方案主要考虑的是目标小区性能的提升，忽略了系统内用户的整体公平性。文献[3]提出一种基于干扰图着色的导频分配方案，但阈值选取的好坏将会直接影响导频分配的效果。文献[4]构建不同小区间用户的加权边干扰图，用此来描述导频污染的程度，运用图着色理论，为受导频污染影响严重的用户优先分配导频。文献[5]提出一种自适应导频分配算法，根据大尺度衰落系数，将系统中所有用户按照对其他小区用户产生的干扰分为大小两个干扰用户组，优先给大的干扰用户组分配正交的导频序列，仿真结果表明，相比于传统的导频分配算法，可以有效提高系统的性能。文献[6]提出一种基于用户位置信息的位置感知导频分配方案，给有最小视距干扰的用户分配相同的导频，有效地提高了系统上行和速率。文献[7]中提出3种导频调度方案，包括贪婪算法、禁忌搜索算法和贪婪禁忌搜索算法。

本文提出基于博弈论的导频分配算法，以最小化系统干扰为目标，设计效用函数和潜在函数。仿真结果表明，该算法具有良好的抗干扰能力。

1 系统模型

本文考虑的是由M个小区组成的大规模MIMO系统，在该系统中，每个小区中的基站配备N根天线，并且，每个小区中有K个单天线用户。

第m小区的用户k到第j基站的信道模型为

(1)

式中，h,j为N×K的小尺度衰落信道矩阵；β,j为大尺度衰落系数，可以表示为

(2)

式中，r,j为m小区用户k到第j小区基站之间的距离；α为路径损耗系数；z,j为m小区用户k到第j小区基站之间的阴影衰落。

大规模MIMO系统模型如图1所示，在上行链路中，由于不同小区的用户采用了相同的导频序列，目标基站就会接收到来自邻近小区的干扰信号，这些干扰信号就会使目标基站对目标用户的信道估计结果造成影响。

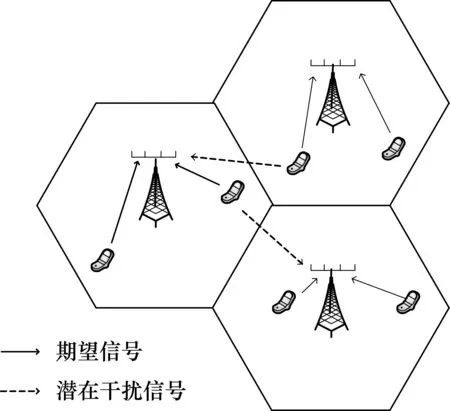
图1 大规模MIMO系统模型

所有小区复用一套相同的导频集，amk代表m小区用户k所使用的导频序列。

定义一个函数：

(3)

即当小区m中用户k和小区j中用户i使用的导频相同时，w函数值为1，也就是两用户存在相互间干扰；否则，为0，两用户不存在相互间干扰。

我们的目标是使系统内的干扰达到最小，即

(4)

subjectto:w(amk,aji)=0m,j∈M,k,i∈K

(5)

2 基于博弈论的导频分配

导频的选择问题可以认为是基站间的博弈。定义一个博弈G=(B,A,U)，其中，B是所有基站的集合，A代表导频分配的集合，Ai∈A表示基站i的导频分配策略，U是效用函数，Ui∈U表示基站i的效用函数，它与本小区内用户使用的导频策略和邻近小区用户使用的导频策略有关。

2.1 构建效用函数

本文中效用函数不仅考虑了小区内用户受到的干扰，同时也考虑给其他小区内用户造成的干扰，将效用函数表示为

(6)

其中，

(7)

表示j小区用户i受到的干扰，式中v代表噪声；

(8)

表示j小区用户i对其他邻近小区造成的干扰。

2.2 构建潜在函数

为了使系统内的整体干扰水平最小，在设计潜在函数时考虑了整个系统的效用，设计的潜在函数如下：

(9)

潜在博弈是博弈论中的一种特殊博弈类型，总会收敛于一个纳什均衡[8]。如果一个博弈存在一个潜在函数能满足式(10)，则这个博弈就是一个潜在博弈[9]。

(10)

下面证明本文中的潜在函数满足式(10)。其中导频分配策略改变时，用户受到的干扰和产生的干扰会发生改变。

(11)

(12)

j基站在采用导频策略A和A′时，所经受的干扰差等于系统内其他用户对其所产生的干扰差，即

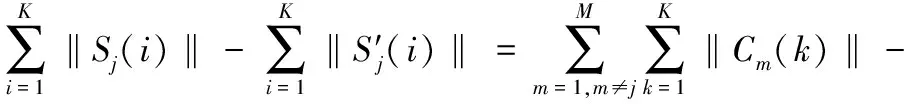
(13)

同理j基站在采用导频策略A和A′时，所产生的干扰差等于其他用户经受的干扰差，即

(14)

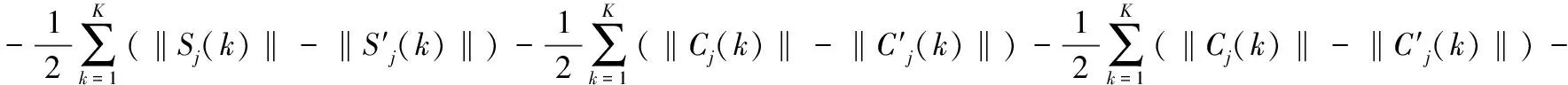
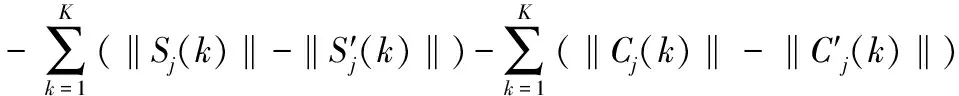
(15)

从式(15)中可以看出，潜在函数式(9)满足式(10)，也就是说该博弈是一个潜在博弈，能够收敛于一个纳什均衡。

2.3 算法步骤

由于大尺度衰落是影响系统性能的主要因素，所以，可以利用基站位置、用户位置来衡量干扰的大小。

① 所有基站随机分配导频，设置基站编号为i=1。

② 基站i计算不同导频分配方案的效用函数，将效用函数最大值对应的导频分配作为此基站的分配策略。

③ 基站i更新自身的导频分配。

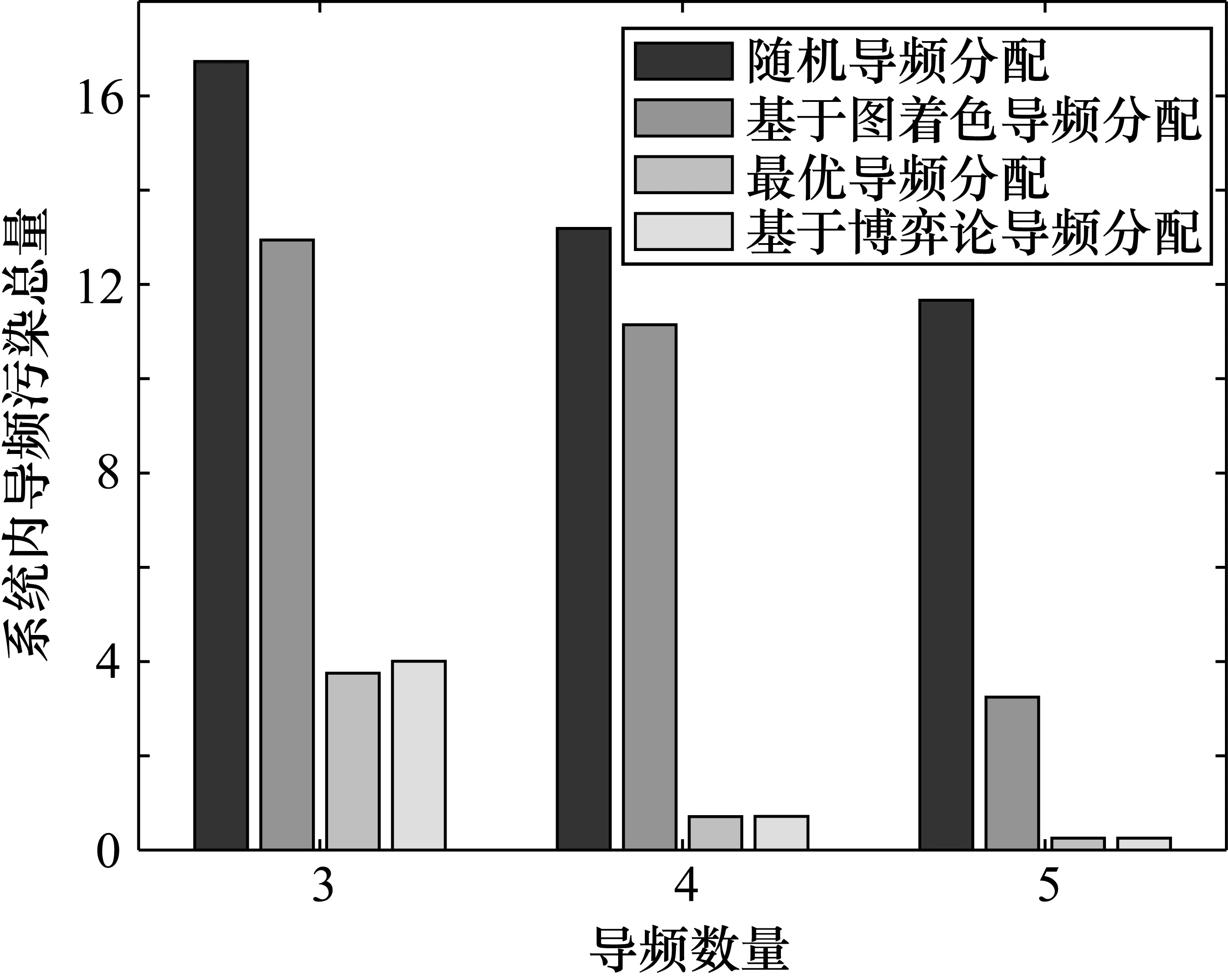
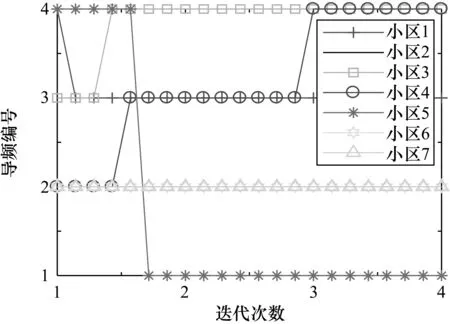
④ 如果i

⑤ 如果每个基站的导频分配列表和上一次迭代相同，则算法收敛，或者迭代的总次数达到了规定的迭代次数的最大值，则结束迭代；否则，令i=1，返回步骤②。

3 仿真结果与分析

本文利用蒙特卡罗法对所提的基于博弈论的导频分配方案进行仿真分析。仿真中考虑的是由M个小区组成的蜂窝系统，每个小区中包含K个单天线用户，每个基站配备N根天线。每个小区中随机生成K个用户的位置，m小区用户k到基站l的大尺度衰落系数通过式(2)随机生成。系统的参数如表1所示。

表1 仿真参数

系统中导频的污染总量和导频数量的关系如图2所示。仿真中，小区数为4，每个小区用户数为2，用户随机分布在各个小区中。从图中可以看出，随着导频数的增加，即每个小区中可利用的导频序列增多时，系统内的干扰量相应地减小。当导频数固定时，本文所提出的基于博弈论的导频分配方案的干扰明显小于传统的随机导频分配的干扰，并且性能近似于最优导频分配。同时可以发现，在导频数为3时，本文所提方案的导频污染量减小到文献[4]中加权边图着色导频分配方案污染量的1/3，这是由于本文所提方案将效用函数最大值对应的导频作为基站的分配策略，通过博弈动态地改变分配结果，直到系统内的导频分配达到一个相对稳定的状态，从而减小了系统内的导频污染量。

图2 导频污染量

小区导频策略变化如图3所示，描述了用户的导频分配情况。仿真中，小区数为7，导频数为4，每个小区中随机分布一个用户。从图中可以看出，随着迭代次数的增加，小区内用户使用导频的变化情况。每次迭代中系统内所有用户都遍历一次，在每次迭代的最后一个基站进行导频分配前，前面基站的导频分配策略不变。为了避免曲线重叠在一起不方便进行观察，绘制仿真图时，在每一条曲线的横坐标加上一个适当的偏移量。

图3 小区导频策略变化

仿真结果表明，本算法在3次迭代内收敛，收敛速度比较快。从图中可以看出博弈的详细过程，小区1中用户随机分配使用导频4，在计算其效用函数后，改变导频分配策略，选择导频3；小区4中用户随机分配使用导频2，在计算其基站效用函数后，先使用导频3，后又使用导频4。上述过程说明，在用户数较小时，算法在迭代到一定次数后，导频分配的策略将不会发生改变，即达到了均衡，这说明算法的收敛性较好。