基于信息熵和灰色关联分析法的集装箱海运网络关键节点识别

2019-09-20陈汨梨李子剑邓夕贵封学军蒋鹤

中国港湾建设 2019年9期

陈汨梨，李子剑，邓夕贵，封学军，蒋鹤

（1.中国港湾西部非洲区域公司，科特迪瓦阿比让 06BP6687；2.河海大学港口海岸与近海工程学院，江苏南京 210098）

0 引言

海运网络是由港口作为节点和航线作为边组成的复杂网络。在采用复杂网络的研究方法对海运网络进行研究的过程中，学者们发现其具有“小世界”和无标度的统计特性[1-2]，目前利用复杂网络理论对海运网络进行研究正是国内外研究的热点。

田炜等[3]对马士基航运集团旗下的海运网络进行分析，证明了该网络的小世界与无标度特性，并指出该网络与其他复杂网络存在差异；邓贵仕等[4]对全球海运网络鲁棒性和脆弱性进行了研究，通过随机删除以及选择度值较大的节点优先删除，发现全球海运网络具有较好的鲁棒性，但网络较脆弱；赵宇哲等[5]从生态学视角出发，运用具有无标度特征的BA模型进行集装箱海运网络演化分析，研究表明集装箱海运网络演化具有“优胜劣汰”的特征；蒋鹤等[6]以海运网络的社团结构为对象研究，构建了“二十一世纪海上丝绸之路”无向无权海运网络模型，研究结果指出“海丝之路”集装箱海运网络为巨型社团结构，且具有核心节点；Tsiotas D等[7]对地中海邮轮网络的港口运营和地理动态进行了深入的分析，并对邮轮公司的空间网络进行了效率比较；Mou等[8]构建了集装箱、邮轮和散货船的海运网络拓扑结构，并对海上丝绸之路海运网络区域贸易关联的空间格局进行了分析；Liu等[9]介绍了加权自我网络分析（WENA）的方法，在全球和地方层面上可视化海运网络的空间异质性，构建了世界海运网络的拓扑连通图，并对其结构特性进行了分析；Calatayud A等[10]采用多网络模型和分析方法，证明了多层海运网络的结构，根据各国在网络中所处的不同位置，对国际货运流造成了不同程度的脆弱性；Zhang等[11]以世界海运网络为研究对象，分析了网络的链路特性，并从饱和性、冗余度等多个方面研究了世界海运网络的统计特性；Kang D J等[12]分析了主要班轮公司港口的网络特征与吞吐量之间的关系，指出吞吐量性能不仅取决于宏观经济变量和服务能力，还取决于网络中港口的中心性。

以上国内外学者的研究重点多着眼于网络整体拓扑性质等宏观层面的普适规律，而鲜有着眼于网络节点等微观层面去解释不同网络所具有的不同特征。由于海运网络的节点之间具有明显的差别性，因此有关节点间的深入比较分析，进行关键节点识别显得尤为重要。本文基于复杂海运网络的拓扑特性和现实背景，提出识别海运网络关键节点的评估指标，即度中心性、介数中心性和港口集装箱吞吐量；接下来构建基于灰色关联法的节点重要度评估模型，并用熵权法确定模型中各指标的客观权重；最后以海上丝绸之路集装箱海运网络为案例验证所提出的指标与识别模型的有效性。

1 集装箱海运网络节点重要度指标

目前国内学者的研究，对于网络中确定节点重要度一般采用单一评价指标，使用最多的包括度中心性、介数中心性、PageRank值、网络效率、最小生成树指标等[13]。复杂网络拓扑结构的非同质性决定了网络中每个节点的重要度是存在巨大差异的，以上的评价指标本质上都是源于图论以及图的信息挖掘，未考虑集装箱海运网络现实物理指标对节点重要度的影响。因此，选择度中心性、介数中心性以及港口集装箱吞吐量作为指标。

2 集装箱海运网络节点重要性综合评价方法

基于信息熵和灰色关联法的集装箱海运网络节点重要性综合评价法是将海运网络中的每一个港口节点视作一个方案，将评价港口节点重要性的多个指标分别看作各方案的属性，则港口节点的重要性评价就转换为一个综合评价问题。海运网络中有m个港口节点，采用n个评价指标，则评价矩阵为 Xij=（xij）m伊n，i=1，2，3，…，m；j=1，2，3，…，n。

2.1 指标标准化

由于不同变量具有不同的单位和变异程度，不同单位会使系数的变量之间的解释发生困难。为了对比变量之间的关系，需要对相应指标数据进行标准化处理。由于均为正向指标，使用极大化法将所有指标数值转化为0~1之间的标准值Pij。

2.2 熵权法

在综合评价指标体系中，由于每个评价指标的作用、地位和影响力不尽相同，必须根据每个指标的重要程度合理的赋予不同的权重。权重反映了各个指标在指标集中的重要性程度。指标的权重直接关系到这一指标对总体的贡献性大小。因此，确定各指标的权重，是综合评价的基础。

根据信息熵理论，某指标的信息熵越小，表明其贡献的信息量越多，权重也越大。各指标的熵值Ej（0臆Ej臆1）为

特别地，当Pij=0时，令Pijln Pij=0。wj为各指标权重

2.3 灰色关联法

灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密，曲线越接近，相应序列之间的关联度就越大；反之就越小。利用灰色关联法进行评价时，可以先引入一个输入最小输出最大的理想对象作为参考序列（母序列），求出各对象（子序列）对参考序列（母序列）的关联度。

母、子序列分别为X0（t）={x0（1），x0（2），…，x0（n）}和Xi（t）={xi（1），xi（2），…，xi（n）}，（i=1，2，3，…，m），则称：

为序列X0（t）与Xi（t）在第i个评价对象在第j个指标的关联系数。式中，籽沂[0，1]，称为分辨系数，一般籽取0.5。

2.4 评价方法的基本步骤

按照集装箱海运网络关键节点评价体系及各因素评价准则，计算节点重要度。计算步骤如下：

第1步：利用公式（1）将所有指标数值转化为0~1之间的标准值。

第2步：确定指标权重。利用公式（3）计算各指标权重wj。

第3步：计算灰色关联系数。

第4步：得出灰色关联度。各港口节点的灰色关联度C

其中 W={w1，w2，…，wn}，R={r1，r2，…，rm}。

3 案例分析

本文数据来源于中国国际海运网（http：//ship.shippingchina.com/）的集装箱班轮船期数据，时间范围为2017年4—8月。剔除无关港口与航线，构建“二十一世纪海上丝绸之路”（以下简称“海丝之路”）集装箱海运网络，选取“海丝之路”海运网络中的港口为节点，航线作为边，共得到450个港口与6 991条边，构建得到无权无向海运网络拓扑模型，并利用Gephi 0.9.2对网络进行可视化，为方便显示，图1筛选显示了度值80以上的节点所组成的网络。

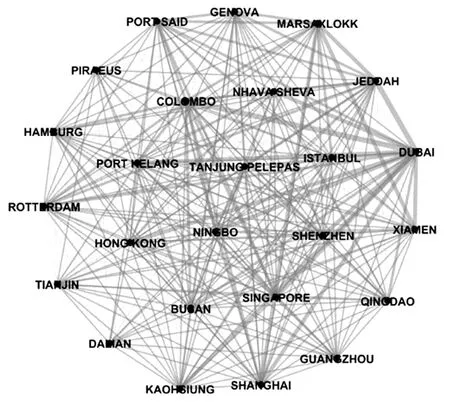
图1 度值80以上港口节点的海运网络拓扑结构Fig.1 Topological structure of shipping network of port nodes with degree above 80

研究表明，5%的核心节点在网络中占据重要地位[14]，由于-始数据过多，在此仅选取各指标下排名前20的港口节点作为研究对象，并使用布尔运算对各研究对象进行并集处理，得到综合评价问题中的研究对象。表1为2017年“海丝之路”海运网络范围内吞吐量排名前20的港口数据。

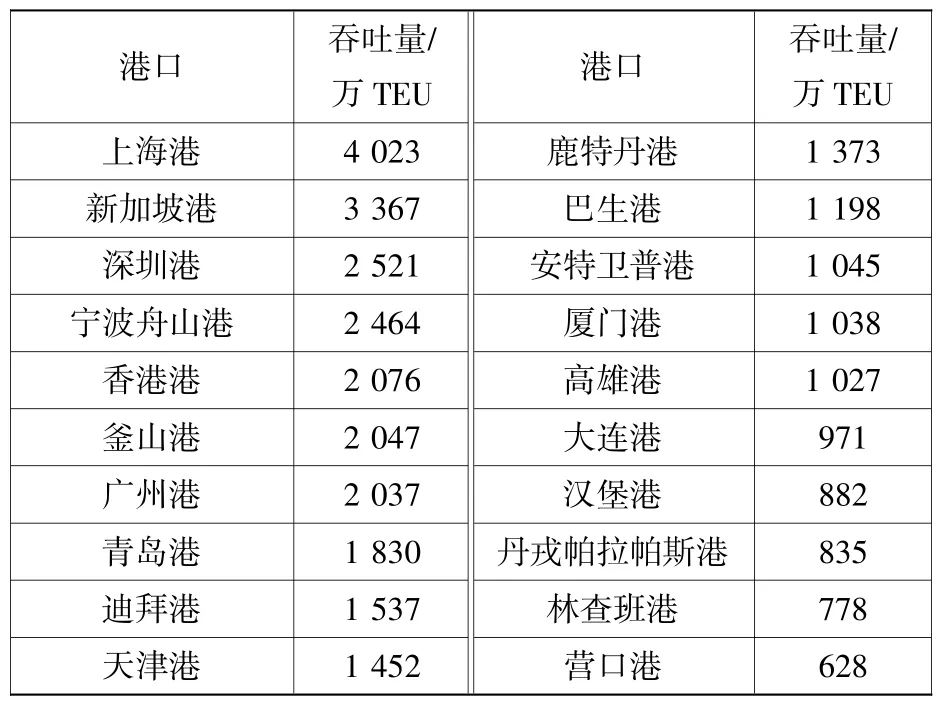
表1 集装箱吞吐量排名前20的港口Table 1 Top 20 ports in container throughput

使用Pajek 5.06a软件进行计算，得到“海丝之路”集装箱海运网络的度中心性、介数中心性，如表2、表3所示。

表2 度中心性排名前20的港口Table 2 Top 20 ports in degree centrality

表3 介数中心性排名前20的港口Table 3 Top 20 ports in betweeness centrality

综上，将所有节点进行并集运算，得到最终纳入综合评价的对象共有27个港口，分别是安特卫普港、巴塞罗那港、釜山港、科伦坡港、大连港、迪拜港、费里克斯托港、热那亚港、广州港、汉堡港、香港港、吉达港、高雄港、林查班港、勒阿弗尔港、马尔萨什洛克港、宁波舟山港、巴生港、塞得港、青岛港、鹿特丹港、上海港、深圳港、新加坡港、丹戎帕拉帕斯港、天津港、厦门港、营口港。

根据集装箱海运网络节点重要性综合评价方法，使用公式（3）计算出各指标权重，如表4。关键港口节点综合评价值，如表5。

表4 评价指标的权重Table 4 Weight of evaluation index

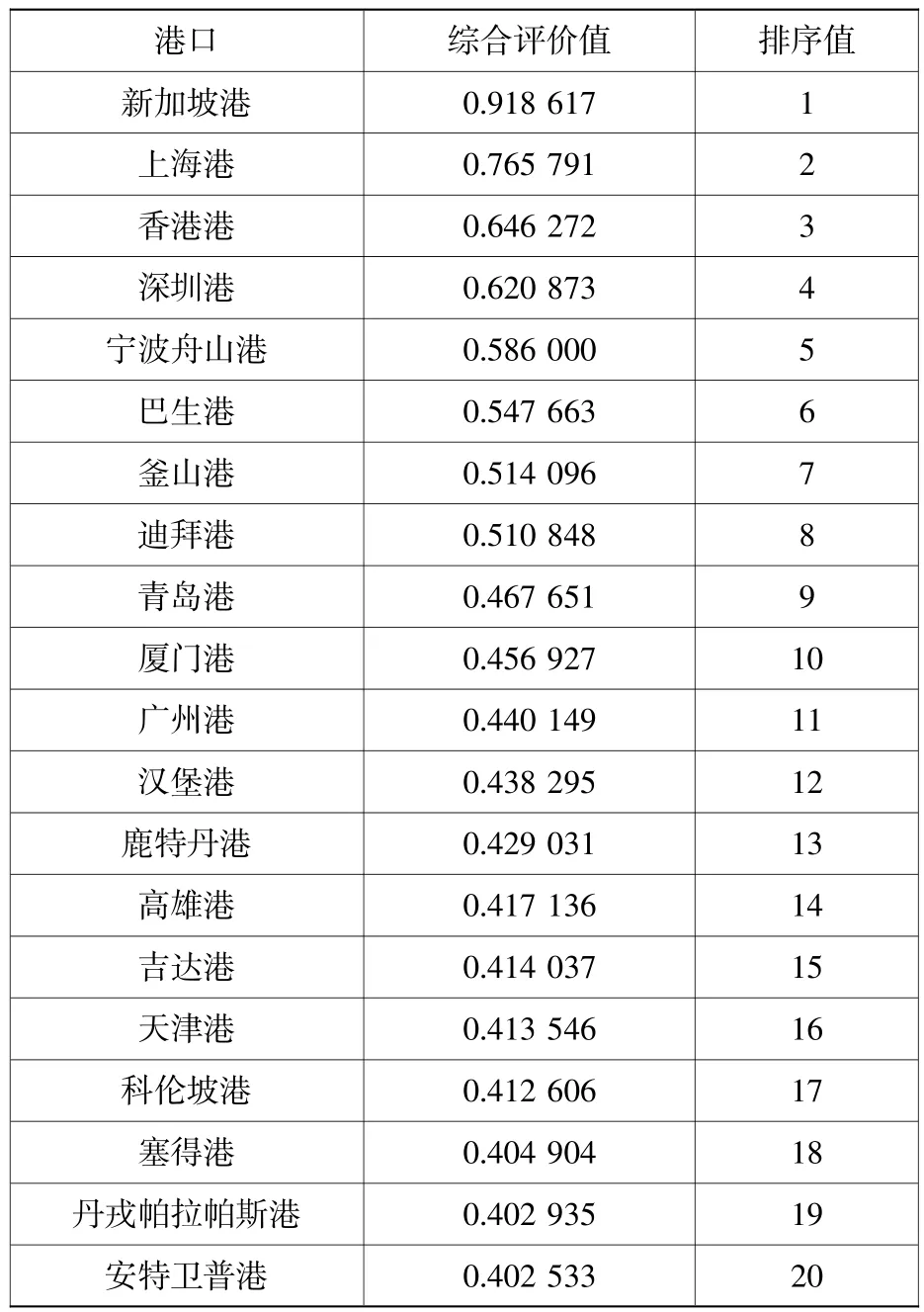
表5 关键港口节点综合评价值Table 5 Comprehensive evaluation value of key port nodes

表5可知，按照综合评价值排序由高到低的港口依次为新加坡港、上海港、香港港、深圳港、宁波舟山港、巴生港、釜山港、迪拜港、青岛港、厦门港、广州港、汉堡港、鹿特丹港、高雄港、吉达港、天津港、科伦坡港、塞得港、丹戎帕拉帕斯港和安特卫普港。

由于本文研究对象为笔者自行收集资料构建的“海丝之路”集装箱海运网络，剥离了美洲与大洋洲，因此在拓扑结构分析中，巴塞罗那港、马尔萨什洛克港、热那亚港以及勒阿弗尔港表现出了重要性，而且指标体系中集装箱港口吞吐量对其进行了一定程度的修正，使案例结果更显可靠性。

除中国大陆的港口外，新加坡港、香港港、巴生港、釜山港和迪拜港均为区域枢纽港与转运港，范围自东向西涵盖了东北亚、东南亚、中东等“海丝之路”重要国家与地区。高雄港、吉达港、科隆坡港、塞得港与丹戎帕拉帕斯港为次枢纽港口，作为主要港口的补充。汉堡港、鹿特丹港和安特卫普港作为西欧港口，距离“海丝之路”主航道较远，重要性也较为落后。这一结果与“海丝之路”战略是一致的。由此可知，采用本文所述方法可指导海运网络关键节点的评估与选择。