考虑铁损的永磁同步电机随机命令滤波控制
2019-09-20于金鹏于海生
程 帅,于金鹏,于海生,付 程
(青岛大学 自动化学院,山东 青岛 266071)
0 引 言
近年来,永磁同步电动机(PMSM)凭借其结构简单、效率高、使用寿命长和实际运用性强等特点,在农业、工业等领域中得到了极为广泛的运用。然而,PMSM的系统具有高度非线性、强耦合和多变量的特点,并且在实际运用中会被不确定的因素所干扰,例如参数不确定和负载扰动。为解决这些问题,相关科技工作者提出了一些先进的非线性控制方法并取得了较好的成效,如反步控制[1-2]、滑模控制[3]和鲁棒控制[4-5]等控制技术。
自适应反步法是解决非线性系统问题的一大突破并成功运用到了PMSM系统中[6],但是在反步控制计算过程中会出现“计算爆炸”的问题。通过近几年的研究,动态面控制(DSC)技术[7]作为新型技术之一被用来解决计算过程中出现的复杂计算,然而DCS技术在实际使用中不能消除滤波误差,这将影响对PMSM的控制精度。2009年,J.A.Farrell 提出了命令滤波技术[8],将命令滤波技术与反步法相结合,避免了反步控制计算过程中“计算爆炸”的问题并减小了滤波误差,文献[9]将命令滤波技术用于非线性系统中,一方面解决了“计算爆炸”的问题,另一方面保证了系统的跟踪误差能够收敛到原点很小的邻域内。近年来,命令滤波技术被用于PMSM控制中[10-11],解决了计算过程中的“计算爆炸”问题,并减小了滤波误差,使控制器的控制精度更高、收敛速度更快和鲁棒性更强。
然而,在上述控制方法中仍然存在一些问题。一方面,电机系统常常会因为高速运行,空载运行或轻载运行产生一定的铁心损耗,这将在一定程度上降低电机系统运行的稳定性。另一方面,电机系统在实际运用中无法避免产生随机扰动的问题,这对电机系统运行过程中的控制效果产生影响。此外,电机的输入饱和问题也会降低系统运行的稳定性[12]。因此,解决电机运行过程中的铁心损耗、随机扰动和输入饱和问题有利于改善PMSM系统的性能。
针对上述问题,本文提出了考虑铁损的PMSM随机命令滤波控制技术,引入伊藤定理处理系统中的随机项,利用神经网络方法逼近系统中的随机非线性函数[13-15],采用自适应命令滤波方法,解决神经网络中的未知参数问题和反步控制中的"计算爆炸"问题,运用分段光滑函数逼近的方法解决了输入饱和的问题。与目前方法相比,本文所提出的方法的主要优点如下:
(1)与文献[9]相比,本文考虑了PMSM系统运行过程中铁心损耗和随机干扰的问题,使设计的控制系统更符合实际工程的需要。
(2)本文采用神经网络方法逼近系统中的非线性函数,并通过使用分段光滑函数逼近的方法解决了输入饱和问题。
(3)与文献[7]相比,本文使用命令滤波技术,有效地处理了反步控制算法中不可避免的 “计算爆炸”问题,并对滤波误差进行补偿。
1 建立考虑铁损的PMSM数学模型
在同步旋转坐标系(d-q)下,考虑铁损的PMSM系统的模型[16]可以描述为:
(1)
式中,ud,uq为定子电压;Θ和ω分别为转子角位置和转子角速度;id,iq为定子电流;iod,ioq为励磁电流。其余参数的定义在文献[16]中具体说明。
为了简化计算过程,定义新的变量如下:
x1=Θ,x2=ω,x3=ioq,x4=iq,x5=iod,x6=id,
引理 1[1]:已知w表示r维标准布朗运动,考虑到随机系统:dx=f(x)dt+h(x)dw,其中f(·)和h(·)是在x上的局部Lipschitz函数。任意给定V(x)∈C2,定义差分运算L,可以得到:
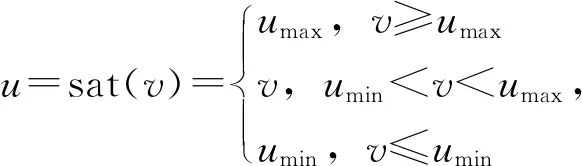



根据引理1和引理2,将上式代入系统中可得:
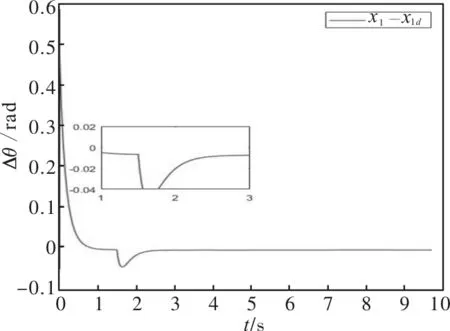
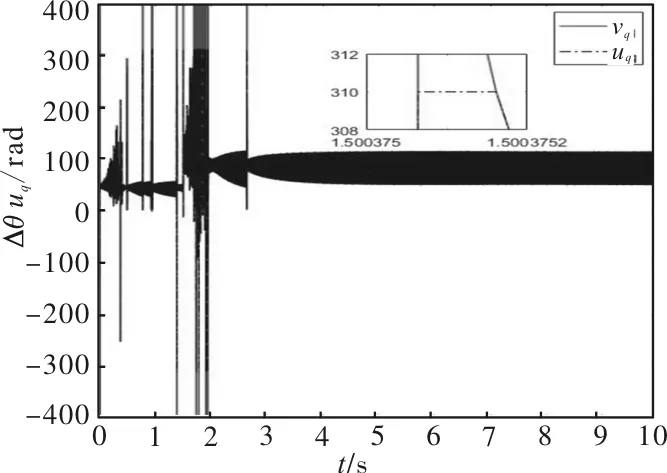
假设1:已知常数bm和bM且满足关系式:0 引理 3[13]:命令滤波器定义如下: 引理 4[14]:对于∀(x,y)∈R2,总存在不等式: 其中,ε>0,p>1,q>1且(p-1)(q-1)=1。 本节将给出基于反步法的随机非线性神经网络控制器的设计。定义系统误差变量: (2) (3) (4) (6) 由神经网络逼近特性[15]和杨氏不等式可得: -b1x3+b2x2x5+b3x2 (7) (8) 由神经网络逼近特性[15]得: (12) (14) 由神经网络逼近特性[15]得: 选取D=max{Dq,Dd},代入式(14)可得: 由上述分析,选择Lyapunov函数如下 (16) 其中,a0=min{4e1,4e2,4e3,4e4,4e5,4e6,p2,p3,p4,p5, (18) 综上所述,通过调整参数a0,b0,k0和σ2可以使z1收敛于原点周围期望的邻域内。 为了验证所提出的考虑铁损的随机命令滤波控制技术在PMSM控制系统中的有效性,通过使用Matlab2016进行仿真实验。选择PMSM的参数: J=0.002 kg·m2,λPM=0.0844 Wb,Lld=0.00177H, Rc=200 Ω,Ld=0.00977 H,Lq=0.00977 H,np=3, Lmd=0.007 H,Lmq=0.008 H,Llq=0.00177 H,R1=2.21 Ω。 ξ1=ξ3=0.7,ξ2=ξ4=0.9,ω1=ω3=500,ω2=ω4=800。 仿真结果如图1~图8所示 。 图1 系统的状态变量和参考信号(命令滤波) 通过仿真得出系统的仿真图,其中图1和图2分别表示在使用命令滤波方法和动态面方法下的状态变量和参考信号的跟踪波形变化。 图2 系统的状态变量和参考信号(动态面) 图3 跟踪误差x1-x1d(命令滤波) 图4 跟踪误差x1-x1d(动态面) 图5 系统输入ud的轨迹(命令滤波) 图6 系统输入ud的轨迹(动态面) 图3和图4分别表示在使用命令滤波和动态面方法下位置跟踪误差的波形变化,图5~图8分别表示在使用命令滤波方法和动态面方法下输入ud和uq的波形变化。 图7 系统输入uq的轨迹(命令滤波) 图8 系统输入uq的轨迹(动态面) 与文献[7]中提出的动态面控制方法相比,命令滤波控制方法的跟踪效果更好,跟踪误差更小,收敛速度更快,鲁棒性更强。 本文在考虑铁损和随机扰动的情况下,将神经网络技术与自适应命令滤波技术结合,解决了"计算爆炸"问题,实现了PMSM的随机非线性控制。仿真结果表明该方法能够更好地跟踪预期的位置信号,并提高了系统的鲁棒性。本文提出的方法为永磁同步电机的广泛应用提供了理论依据。

2 PMSM系统控制器设计






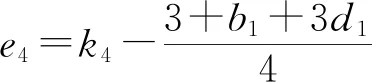
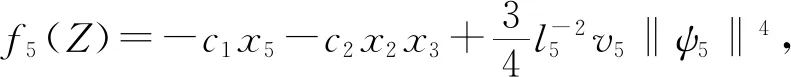
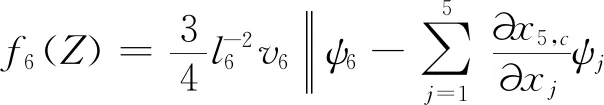
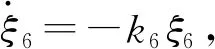
3 稳定性分析




4 对比实验研究







5 结 语
