解读双动点轨迹之线段最值问题的捆绑变换
2019-09-19李登位
李登位
(湖北省恩施市龙凤民族初级中学 445000)
一、前言
所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.从变换的角度和运动变化来研究三角形、四边形、函数图象等几何图形,通过“图形变换、动点的运动”等研究手段和方法,来探索与发现图形性质及图形变化,在解题过程中渗透空间观念和合情推理.选择基本的几何图形,让学生经历探索的过程,以能力立意,考查学生的自主探究能力,促进培养学生解决问题的能力.在动点的运动过程中观察图形的变化情况,需要理解图形在不同位置的情况,才能做好计算推理的过程.在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质.
二、举例解析
数学卷中的数学压轴题中涉及数形结合、动态几何、动手操作、实验探究等方面题型较多、题意创新,目的是考查学生的分析问题、解决问题的能力,内容包括空间观念、应用意识、推理能力等,更好地培养学生解题素养.
线段最值问题最常见的就是定点到动点最大距离或最小距离问题.因此,解决这类问题的关键在于弄清楚动点运动的轨迹.下面学习如何利用“捆绑变换”思想来探寻动点轨迹,从而解决线段的最值问题.
例1如图1,矩形ABCD中,AD=2AB=4,长度为2的动线段AE绕点A旋转,连接EC,取EC的中点F,连接DF,求线段DF长的最大值和最小值.
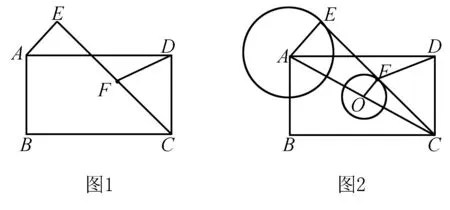

例2如图2,AB=4,O为AB的中点,⊙O的半径为1,点P是⊙O上一动点,以点P为直角顶点作等腰三角形△PBC(点P、B、C按照逆时针方向排列),则线段AC长的取值范围是____.
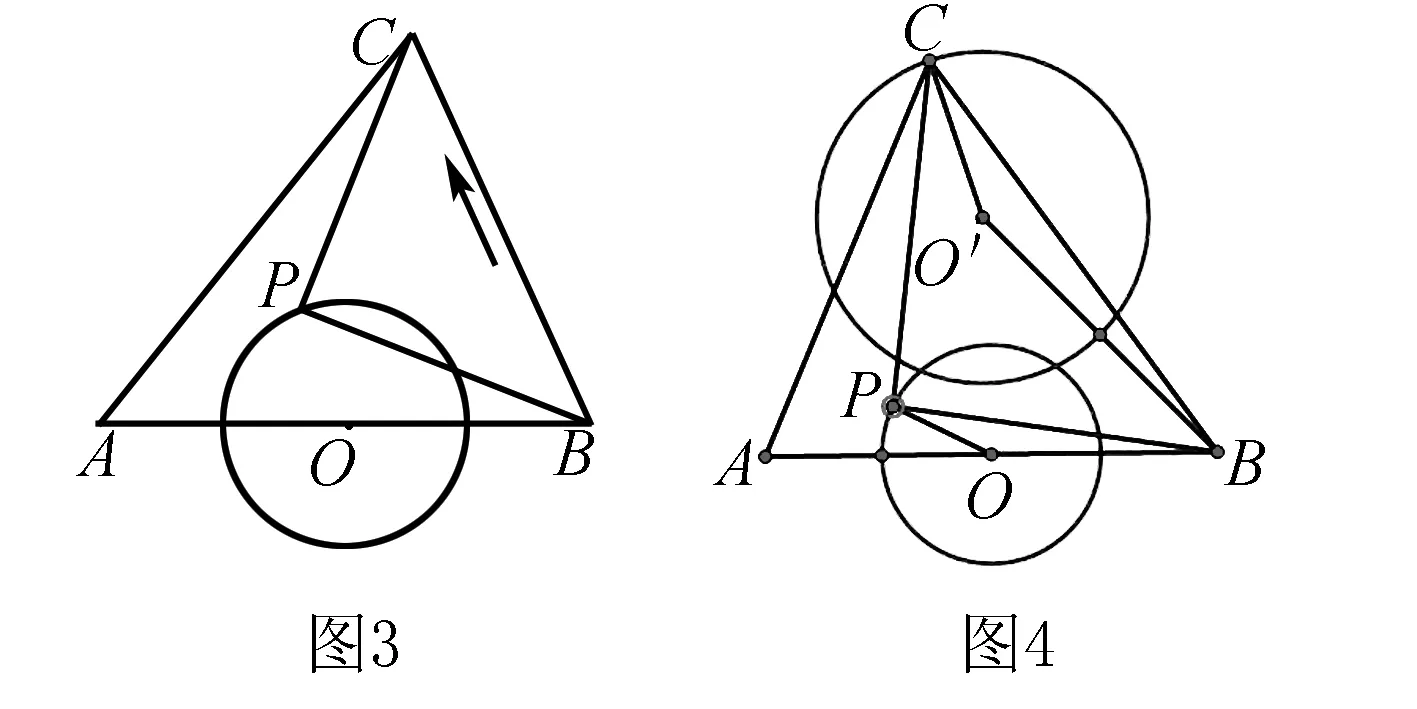

例3如图,点O为坐标原点,⊙O的半径为1,点A(2,0).动点B在⊙O上,连接AB,作等边三角形△ABC(A、B、C为顺时针顺序),求OC的最大值与最小值.

思路分析需要明白从主动点B到从动点C是作了怎样的变换?利用几何画板观察到,将点B绕着点A按照顺时针方向旋转60度得到点C,再找从动点C所在圆的圆心和半径,捆绑OB作相同的变换,即:将点O绕着点A按照顺时针旋转60度得到点O′,即以OA为边向上作等边△OAO′,则点O′就是点C所在圆的圆心,半径为O′C.连接BO、CO′,因△ABC和△OAO′均为等边三角形,则AO=AO′,AB=AC,∠BAO=∠CAO′,得△ABC≌△OAO′,CO′=BO=1,点C在以O′为圆心,1为半径的圆上运动,而OO′=AO=2,CO′=BO=1,所以CO的最大值为3,最小值为1.
以双动点为载体,图形为背景,运动变化为主线创设的求线段最值问题,集多个知识点为一体,集多种解题思想于一题,要求学生认真读题、领会题意、画出不同情况下的图形,判断动点运动轨迹的形状是解题的关键,根据图形建立变量之间的关系,要求学生有扎实的基础知识、灵活的解题方法、良好的思维品质;在解题思想上着重对数形结合思想、分类讨论思想、数学建模等思想的灵活运用.要以静代动的解题思想解题.