基于决策树与扩展相关性矩阵的故障诊断方法

2019-09-19

测控技术 2019年7期

(1.上海科学技术职业学院机电工程系，上海 201800； 2.北京航空航天大学可靠性与系统工程学院，北京 100191；3.防灾科技学院后勤管理处，河北廊坊 065201)

随着现代电子产品集成化、小型化、多样化的发展，其结构越来越复杂，同时也带来了故障测试与故障诊断等问题，故障诊断技术受到了广泛的关注[1]。

故障诊断技术的主要目的是检测影响系统安全性能的故障，并准确隔离故障。目前电子设备故障诊断方法主要包括基于智能算法的故障诊断方法以及基于相关性矩阵推理的故障诊断方法。

在基于智能算法的故障诊断方法方面，张瑞[2]等人将BP神经网络模型应用于某型地空导弹静变电源的故障诊断中。为解决神经网络训练需要大量的样本、易陷入局部最优、收敛速度慢等缺点，张松兰[3]等人提出了改进模糊聚类(IFC)和支持向量机(SVM)相结合的模拟电路故障诊断方法。针对现有地铁车门故障诊断方法存在的诊断速度慢以及大量故障检修数据未得到合理利用等问题，陈苏雨[4]等人提出了一种基于信息增益率的随机森林故障诊断方法。

基于D矩阵的故障诊断方法属于测前仿真故障诊断方法，作为目前较为流行的故障诊断方法，其基本思想是根据预先的实际经验或实际需求确定产品的潜在故障集合，然后通过计算机仿真或实物的故障注入手段，求取产品在各个状态下的响应[1]，用0/1值表示测试与故障之间的关系,构建故障与测试的一阶相关性矩阵，其中0表示测试未检测到故障，1表示测试检测到了故障。在诊断推理的过程中，通过BIT给出的0-1判定结果，结合预先构建好的相关性矩阵进行故障隔离推理，确定产品的状态。

目前基于D矩阵的故障诊断方法已得到了广泛的应用。田恒[5]等人在D矩阵的基础上提出了一种基于单故障化的多故障诊断与维修新策略。为了提高D矩阵故障诊断的效率，在继承D矩阵传统处理算法优点的基础上,引入局部信息熵算式，进一步提出一种信息熵测试性D矩阵故障诊断新算法；林志文[6]等人利用D矩阵分别完成对舰船电子装备的测试性分析评估、诊断测试序列生成,实现了某舰船电子装备综合诊断。

此外，为进一步扩展D矩阵的应用，传统D矩阵与智能算法的结合运用在故障诊断上也取得了很好的效果。郑博恺[7]等人将支持向量机与D矩阵结合，提出了一种基于故障测试相关矩阵与支持向量机的模拟电路软故障诊断方法；石君友[8]等人结合D矩阵与模糊理论，通过构建增强推理算子与模糊相关性矩阵实现故障诊断。

然而，由于传统的D矩阵用逻辑0/1表示故障与测试的相关关系，表示方式简单，简化了故障推理，而从另外一个角度考虑，其简单的0/1关系仅仅表示了故障与测试之间有无关联，而无法进一步描述故障与测试之间关联的程度，且无法充分利用和挖掘测试与故障间的相关性，因此基于传统D矩阵的诊断推理方法在故障隔离能力将受到限制。基于以上考虑，本文借鉴测前仿真故障诊断方法的基本思想，为充分利用测试的信息，在D矩阵的基础上提出了扩展D矩阵的概念，并给出了构建方法，将扩展D矩阵与决策树算法结合，建立了决策树模型，实现了故障检测与隔离，并以电源模块为案例进行了应用，结果表明该方法相比于传统D矩阵方法具有更高的故障隔离能力。

1 扩展相关性矩阵构建方法

传统的D矩阵的故障诊断思想是用0/1值表示测试与故障之间的关系，当矩阵中元素为1时，表示该测试可以检测到该故障，0表示对应的测试无法检测到该故障，是对测试与故障关系的定性描述。传统的基于D矩阵的故障诊断方法主要包括相关性模型的建立、测试性分析获取D矩阵、诊断推理三个部分[9]。

在传统的D矩阵中用简单的0/1逻辑量表示测试与故障之间的关系，虽然减少了诊断推理时的计算量，但将其关系简单的抽象为能否检测，显然无法充分利用测试中的信息量，这样将导致诊断推理的结果不够精确。如一个5 V的电压测试，若监测数据为2.5 V或0 V，在D矩阵中对应的元素值都是1，表示该故障可被检测到，这样处理将无法反映监测数据的具体变化，无法充分利用监测数据的信息，从而导致基于该矩阵的诊断推理结果不够精确。

考虑到传统D矩阵的上述缺陷，本文提出了一种扩展D矩阵的构建方法。扩展相关性矩阵不再是用简单的0/1描述故障与测试的关系，而是用多值描述故障与测试之间的关系。测试与故障的扩展D矩阵构建流程主要包括故障集合的确定、测试集合确定、仿真/实物故障注入、数据的野值剔除、数据合并等。

(1) 故障集合的确定。基于故障模式影响和危害性分析(FMECA)工作，梳理出产品的所有潜在故障集合，根据产品故障诊断的要求，确定产品所需诊断与隔离的层次，如按照航空产品划分，在故障模式影响和危害性分析中，系统的结构可以自上而下划分为系统级、外场可更换单元(LRU)级、车间可更换单元(SRU)级、电路板级、功能子电路级和元器件级，相应的故障模式也存在系统级、LRU级、SRU级、电路板级、功能子电路级和元器件级。根据诊断的层次要求，对所有的故障集合进行故障合并分析，从而获得所需的潜在故障集合。

(2) 测试集合的确定。对产品的设计方案进行分析，梳理出产品现有的测试情况，根据故障诊断需求确定需实现的最终测试集合。

(3) 仿真/实物故障注入。故障注入的方式有两种，一种是仿真故障注入，另一种是基于实物的故障注入，前者是基于产品设计基础上，通过仿真软件构建产品的仿真模型，模拟产品的各个故障状态，计算产品的响应；后者是基于产品设计，制作具有故障注入接口的样件产品，利用各种故障注入的技术，借助故障注入设备实现对实物的故障注入。

(4) 野值剔除。获取初始扩展D矩阵，数据的野值剔除方法主要是基于莱特准则判据实施的，分别针对每一个测试点每个状态下获取的测试数据按照下式求取均值和方差。

(1)

(2)

如果|xi-μ|>3σ，则判断xi为奇异点，剔除。具体流程如下：

① 通过计算机仿真或故障注入手段获取第j个状态在第i个测试下的数据集；

② 计算上述数据集的均值和方差；

③ 计算每一个数据的残差，并与3倍的标准差进行比较，利用莱特准则进行野值判别；

④ 若判定为野值，则用前一个样本点替换该样本；

⑤ 按照上述的判定准则，循环多次，直到数据集中无野值点为止；

⑥ 计算无野值后数据的均值，将其作为该状态与测试之间的关系值，放入初始扩展相关性矩阵中；

⑦ 重复上述步骤，遍历所有状态，得到初始扩展相关性矩阵。

(5) 数据合并，获取最终扩展相关性矩阵。在初始扩展相关性矩阵中，行表示状态，列表示测试，每一个状态都有特定的测试值与之对应。然而，在实际的初始扩展相关性矩阵中很可能会出现下述情况：同一个测试点在两个状态下，其数值不相等，但数值相差极小，在实际情况下，由于其数值太接近，用该测试点是无法对这两种状态进行区分的，而在用相关性矩阵进行故障推理时，会认为上述两种状态是可以通过该测试点进行隔离的。为避免上述情况发生，本文提出了一种数据合并的方法，借鉴目前模糊组划分的方法[10]，在电压特征方法中，认为当两个故障产生的电压差的绝对值小于 0.7 V时就认为这两个故障属于同一个模糊组[11]。经过上一步野值剔除后，每一个状态在不同的测试下都对应了一个数值，第i个状态第j个测试点的数值为dij，针对每一个测试点，对各个状态下的数据进行合并，具体流程如下：

① 计算初始扩展相关性矩阵中每一列的数值之间的差值，将差值小于0.7的数据划分到同一组；

② 计算同一组内数据的均值，作为组内元素的最终取值；

③ 通过上述方法，遍历所有测试，从而获得最终的扩展相关性矩阵。

这样，对于同一个测试点，它的取值不再是0和1。同一测试点可以有多种取值，每一组用一个数值进行表示，有多少组就有多少种取值，值的大小用同一组内数据的均值描述。

2 决策树模型及其算法

2.1 决策树模型

决策树是一种基本的分类与回归方法。它最终生成的是一个类似于树的二分模型，它对不同的特征实例的有标记数据进行训练，构建决策树，最终实现对数据的分类过程，可以认为是if-then规则，也可以认为是特征向量与类别之间的一个条件概率分布。决策树模型可读性强、分类速度快。可以通过有标记的数据进行学习，以损失函数最小化的原则构建决策树模型。预测时，决策树模型是根据对新数据的分类实现的。决策树的学习主要包括下面3个步骤：对模型的特征选择、生成决策树、修剪。

决策树模型是以树形结构实现对象的分类。多个节点和有向边一块构建成决策树，节点有内部节点和叶节点两种类型。内部节点表示特征属性，叶节点表示类标签。

2.2 决策树特征选择方法

决策树的生成算法有多种，主要包括ID3算法和c4.5算法，二者最主要的差别是在对特征选取的原则上，ID3是选择信息增益最大的特征作为结点的特征，c4.5是用信息增益比对特征进行优选。信息增益可用数据集合的信息熵与给定特征下数据集的条件熵表示，具体算法如下：假设D为训练数据集，|D|表示样本个数，有K个类Ck，|Ck|表示属于Ck的样本个数，假设特征A有n个不同取值，特征A将数据集D划分为n个子集D1，D2，…，Dn，|Di|为Di的样本个数，子集Di中属于类Ck的样本集合为Dik，|Dik|为Dik的样本个数。

① 计算数据集的信息熵H(D)。

(3)

② 计算特征A对数据集的条件熵H(D|A)。

(4)

③ 计算信息增益。

g(D,A)=H(D)-H(D|A)

(5)

2.3 决策树的学习

对于决策树学习，假设给定训练数据样本集：

DATA={(x1,y1),(x2,y2),…,(xn,yn)}

(6)

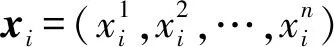
决策树学习是一个递归的选择最优特征的过程，根据这些特征对训练数据进行分割，归纳出一组最好的分类规则，使得数据分类达到最好的效果。其基本步骤如下：

① 创建根节点，将所有数据放在根节点；

② 选择最优特征，将数据分割成子集；

③ 如果这些子集已经能够被基本正确分类，则将这些子集分到所对应的节点上；

④ 如果还有子集不能被基本正确分类，则对这些子集选择最优的特征，继续进行分割；

⑤ 依照上述方法递归进行，直到所有数据子集被基本正确分类为止。

2.4 基于扩展D矩阵的决策树模型

传统的基于D矩阵的故障诊断方法是将D矩阵的一行作为一条诊断知识，将测试序列与D矩阵的行进行比对，找到与其匹配的行，该行所对应的状态，即认定为系统的当前状态。该方法中测试的比对是并行的。基于决策树与扩展D矩阵故障诊断方法，是在扩展D矩阵的基础上进行构建决策树模型，通过决策树特征优选的方法先选出第一步需要进行的测试，然后在剩余的测试中以同样的方法进行测试优选，从而获得一条最优的诊断路径，通过一步一步的测试，得到最终的诊断结果。其基本步骤如下：

① 计算扩展D矩阵中数据集的经验熵；

② 计算各个测试对数据集的信息增益；

③ 比较各个测试的信息增益值，取信息增益最大的测试作为故障诊断推理的第一步测试；

④ 根据上述方法选择第②步测试，直到所有的故障数据被基本正确分类为止。

3 基于决策树与扩展相关性矩阵的电

源模块故障诊断方法应用

案例应用针对多路电压输出的电源模块展开，电源模块主要包括18 V、12 V、5 V、3.3 V、2.5 V、1.8 V和0.9 V等7个电压处理子电路。电源模块的开路故障的注入主要是依靠短路帽实现，参数漂移故障通过探针式故障注入器实现，共注入9个故障，设置了5个测试点，在每个状态下各采集了50个样本数据，共500个样本数据，根据野值剔除方法及矩阵构建方法，可获得初始扩展相关性矩阵如表1所示，行表示状态，列表示测试。

根据上述扩展相关性矩阵的构建方法，对上述矩阵进行数据合并获得最终的扩展相关性矩阵如表2所示。

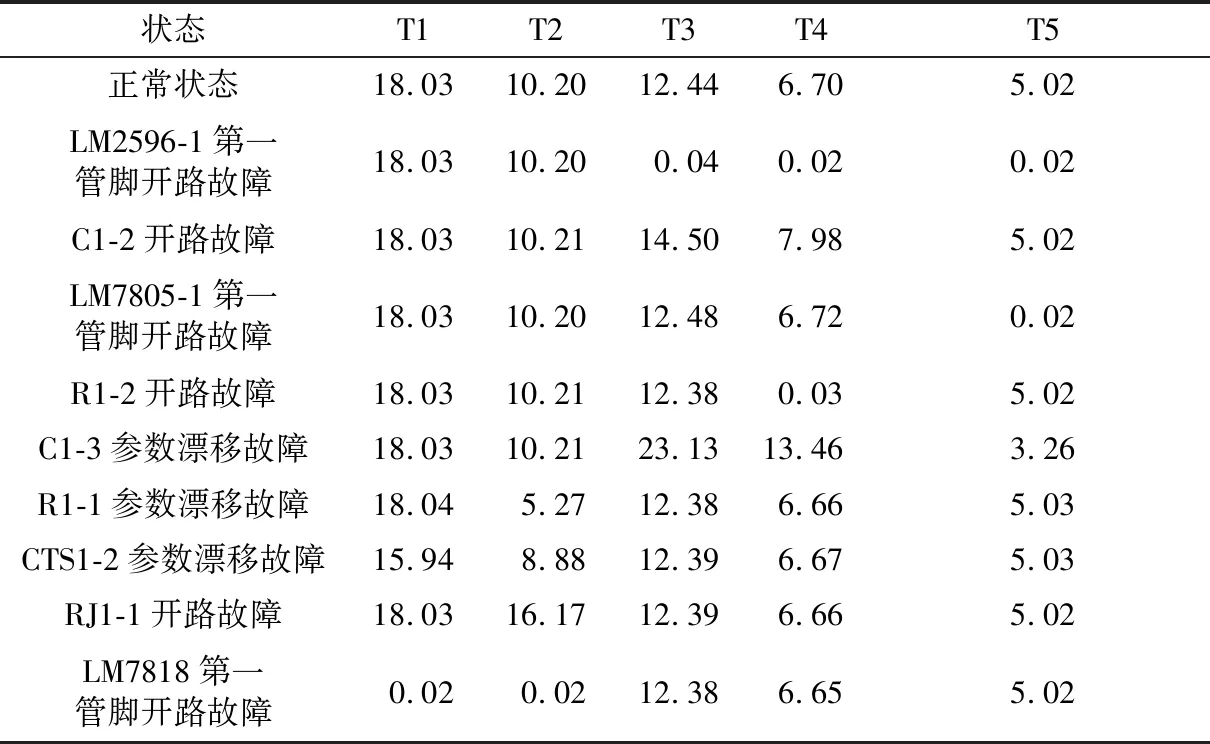
表1 初始扩展相关性矩阵

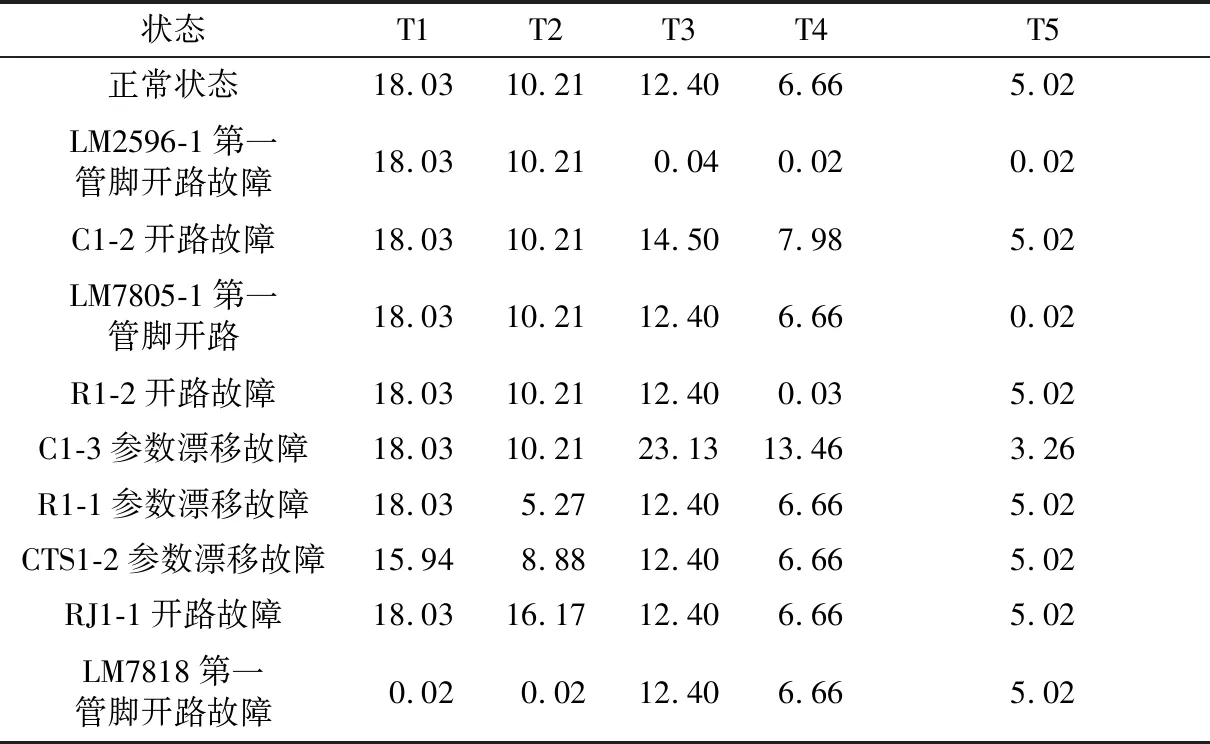
表2 扩展相关性矩阵

按照传统D矩阵方法，构建的D矩阵如表3所示，可以看出LM2596-1第一管脚开路故障与C1-3参数漂移故障在传统的D矩阵中具有相同的行(0,0,1,1,1)，R1-1参数漂移故障与RJ1-1开路故障也具有相同的行(0,1,0,0,0),因此上述两对故障无法通过传统D矩阵的方法进行隔离。

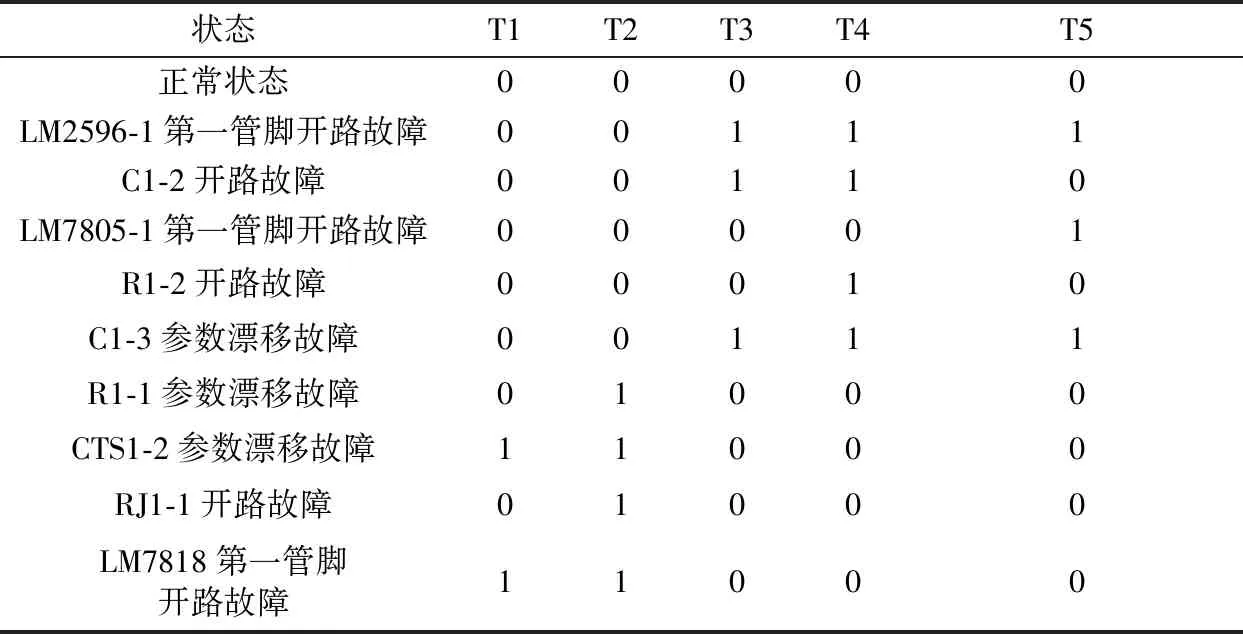
表3 传统相关性矩阵

而在扩展D矩阵中，LM2596-1第一管脚开路故障与C1-3参数漂移故障可用T3、T4、T5中的任意一个测试隔离开，R1-1参数漂移故障与RJ1-1开路故障可用T2进行隔离。

按照第2节构建决策树的方法构建决策树如图1所示。

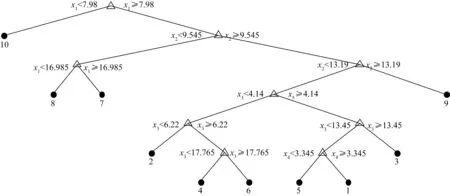
图1 电源模块故障诊断决策树模型

由图1决策树模型可看出，通过5个测试点，可将上述9个故障模式准确的隔离，故障隔离率达到了100%，而基于传统的D矩阵方式，将会出现以下模糊组(LM2596-1第一管脚开路故障,C1-3参数漂移故障)/(CTS1-2参数漂移故障，LM7818第一管脚开路故障)。两种故障隔离方法所得到的故障隔离率指标对比如表4所示。