改进GM(1,1)模型对地铁开挖沉降的预测*
2019-09-19戴文亭王宇放
戴文亭, 王 振, 王宇放, 王 琦
(吉林大学 交通学院, 长春 130022)
城市地铁在施工过程中会对土层造成一定程度上的扰动,从而引起地表沉降,此外,由于城市中建筑密集、地下管线密布、施工条件受限,地表沉降较难控制,因此,满足一定精度的隧道施工引起的地面变形预测方法愈加受到关注[1],已有很多学者就此问题进行了研究[2-3],有限元软件也逐渐开始应用到地表沉降预测[4],而灰色系统理论以其数据少、预测精度高和无需先验信息的特点逐渐受到人们的关注[5],且在各行业均有应用.

本文讨论了建立新陈代谢GM(1,1)模型过程中最佳原始序列的个数,并采用多种方式对原模型进行改进,结合改进模型的预测值对改进模型的适用范围进行了讨论.
1 灰色系统理论
1.1 GM(1,1)模型建立过程
均值GM(1,1)模型(以下简称GM(1,1)模型)是邓聚龙教授最先提出的灰色预测模型,也是目前影响最大,应用最为广泛的模型,模型建立过程[10]如下:
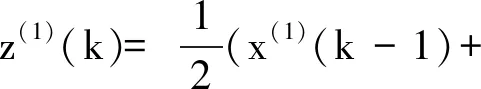
1.2 GM(1,1)模型局限性
1) 原始序列越平顺则模型预测越准确[11],若原始序列上下波动较大则模型预测精度将会降低,原始序列越接近指数函数的分布则模型预测越准确,若原始序列与指数函数的分布相差越大则模型预测准确度越差,因此,在建模过程中要注意原始数据段的选取并需要及时更新数据.
2) 原始模型中背景值由均值生成的Z(1)(k)来代替,而GM(1,1)模型拟合曲线为指数曲线,因此,在区间[k,k+1]上曲线的实际面积要始终小于abcd所未成的梯形面积,如图1所示.其中,x(1)(t)为由GM(1,1)模型拟合曲线的指数函数;x(1)(k)为拟合的指数函数在k处的取值.若原始序列增长速率较慢则两者相差不多,但当原始序列变化急剧时,两者面积差ΔS变大,若仍用Z(1)(k)代替则模型偏差较大,而且为滞后误差.
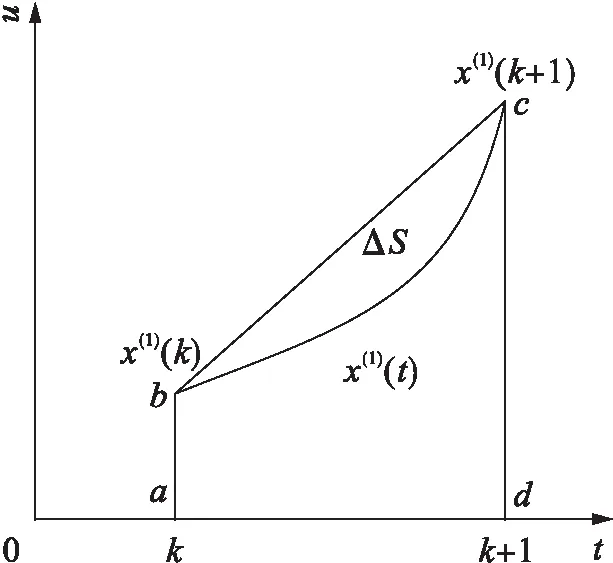
图1 背景值构造示意图Fig.1 Schematic establishment of background values
2 改进灰色系统理论
随着灰色系统理论的不断发展,研究人员在原始模型的基础上不断进行改进优化,对于GM(1,1)的优化改进主要有以下几种方法:改变原始序列的平顺度;改变模型背景值;组合模型.组合模型类型较多,例如与神经网络结合,与时间序列结合等,在此不再赘述.
2.1 最佳原始序列个数
根据灰色系统的基本原理,新信息优先原理,即新信息对认知的作用大于老信息,在建立模型过程中一般采用新陈代谢GM(1,1)模型.新陈代谢模型建立时一般取4~8个数据作为原始序列,在出现新的数据后将其放入原始序列中,并将“老”的信息去掉,最后再进行下一次预测,保证模型中数据个数始终不变.从预测角度分析,新陈代谢模型是最理想的模型,系统在发生变化过程中老的数据已经无法反映系统当前特征,去掉是完全合理的,而且老数据的去除也能减少计算量.取长春地铁二号线暗挖区拱顶地表沉降点进行分析,沉降观测数据如表1所示.
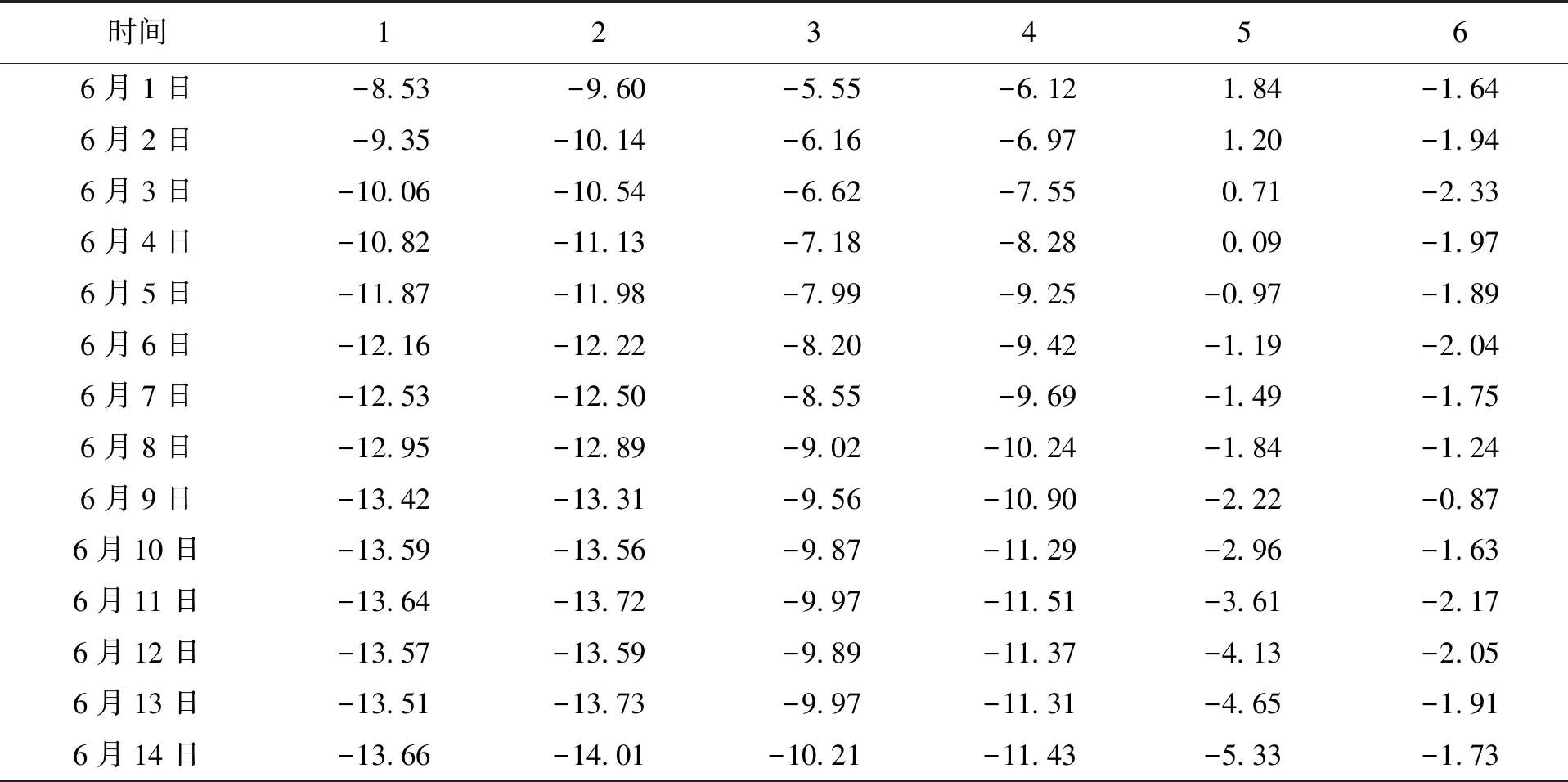
表1 地铁二号线暗挖区拱顶地表沉降Tab.1 Ground surface settlement of vault of metro line 2 undermining area mm
取1号、2号沉降观测点进行分析,根据6月1日~6月10日的累计沉降量对6月11日~6月14日的累计沉降量进行预测,分别取3~8个点(3个点,即6月8~10日,4个点,即6月7~10日,其余依次向前加一天)作为原始序列建立新陈代谢GM(1,1)模型,分别命名为模型3,模型4,,模型8,预测结果及误差如表2所示.
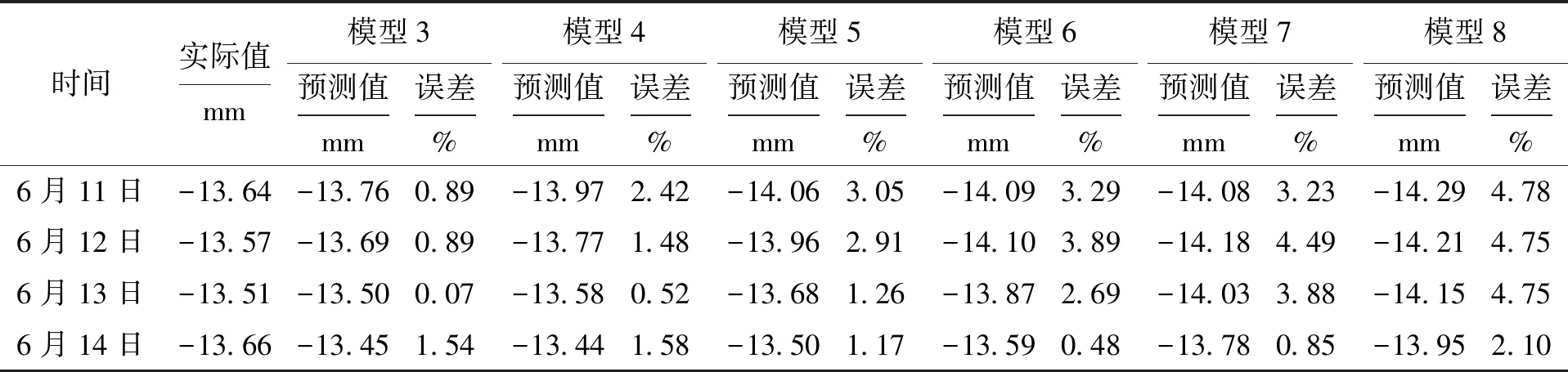
表2 各个GM(1,1)模型对1号点累计沉降量的预测Tab.2 Prediction of cumulative settlement of point 1 in each GM (1,1) model
各个模型预测值的平均误差分别为0.847%、1.500%、2.098%、2.590%、3.112%、4.092%,随着所取点数的增加,平均误差不断增加,实际值与预测值如图2所示.由表2和图2可知,取模型3的预测值与实际值相比无论是在整体走势、预测值上均比较接近,且在与另外几个新陈代谢GM(1,1)模型相比,其平均误差最小,但是该模型对6月14日预测的误差较大且变化趋势与实际相反,这主要是因为实际的累计沉降量曲线在该处变化不平顺.表3为各个GM(1,1)模型对2号点累计沉降量的预测.
与1号点类似,各个模型预测值的平均误差分别为1.445%、1.755%、1.953%、2.210%、2.170%、2.729%,随着所取点数的增加,平均误差不断增加,实际值与预测值如图3所示.
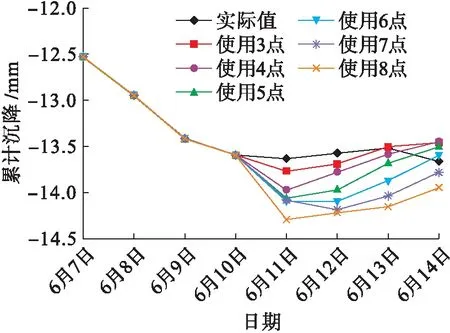
图2 1号点累计沉降实际值与预测值Fig.2 Measured and predicted values of cumulative settlement of point 1
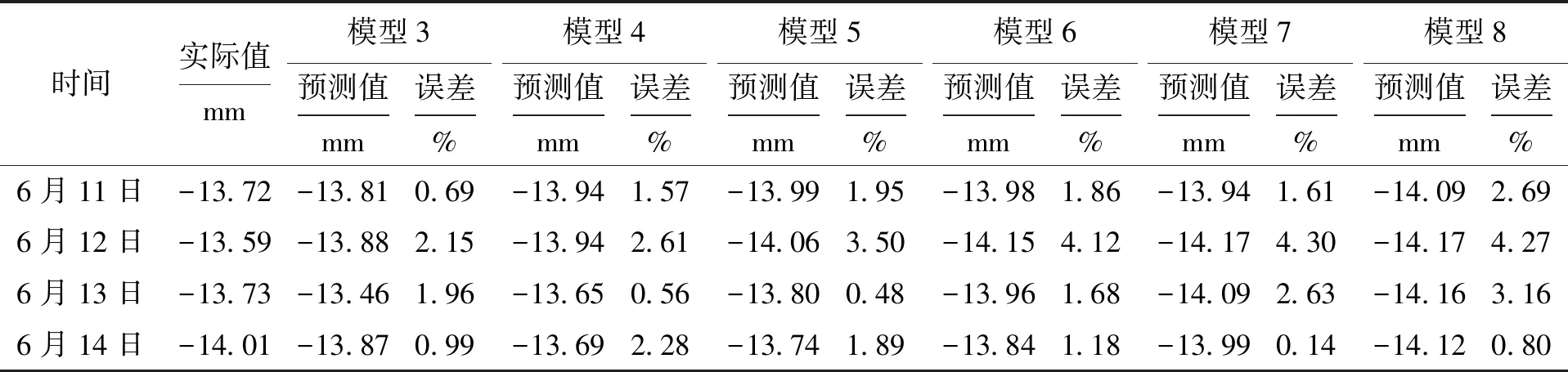
表3 各个GM(1,1)模型对2号点累计沉降量的预测Tab.3 Prediction of cumulative settlement of point 2 in each GM (1,1)model
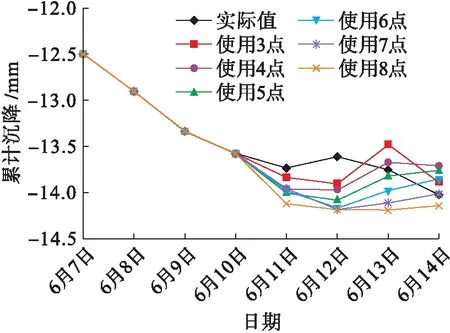
图3 2号点累计沉降实际值与预测值Fig.3 Measured and predicted values of cumulative settlement of point 2
由表3和图3可知,取3点建立的新陈代谢GM(1,1)模型的预测值与实际值相比,6月11日~6月13日走势相反,而且对6月13日的预测偏差较大,这主要是因为实际累计沉降量变化不平顺且趋势不断变化.采用同样的方法对5号点、6号点进行处理,实际值与预测值如图4、5所示.
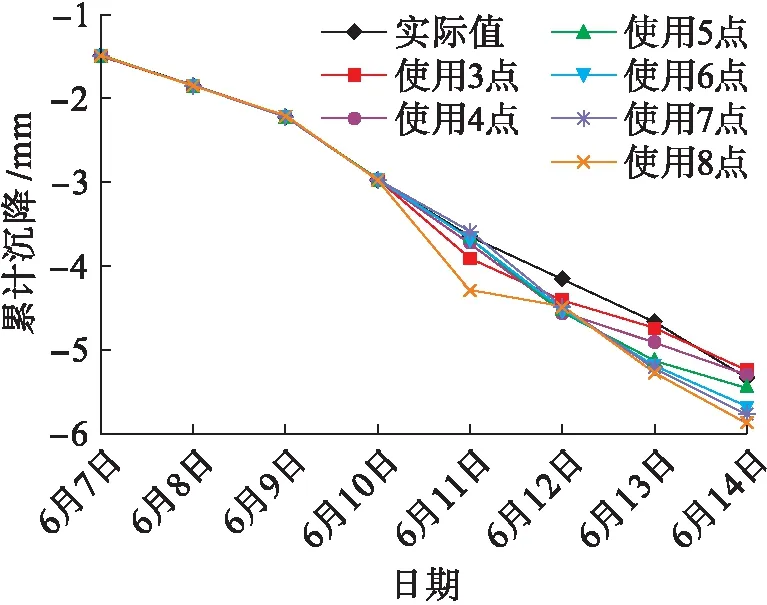
图4 5号点累计沉降实际值与预测值Fig.4 Measured and predicted values of cumulative settlement of point 5
对比分析模型3对5号点、6号点的预测可知,当原始序列变化平顺时除了模型8之外各个模型预测值虽然有优有劣,但是相差不大,当原始序列较为曲折时,各个模型的预测值相差变大.通过对比分析各个新陈代谢模型对以上4个点的预测可以发现,相对其他模型,模型3平均误差相对较小,且对数据变化特别敏锐,但是当在某次出现极值时,对下一次预测模型的趋势和精度均会出现误差,尤其是连续出现极值时误差与预测趋势偏差更大,如模型对2号点和6号点累计沉降量的预测,当不出现极值时模型3对原始数据的预测一般会偏大.
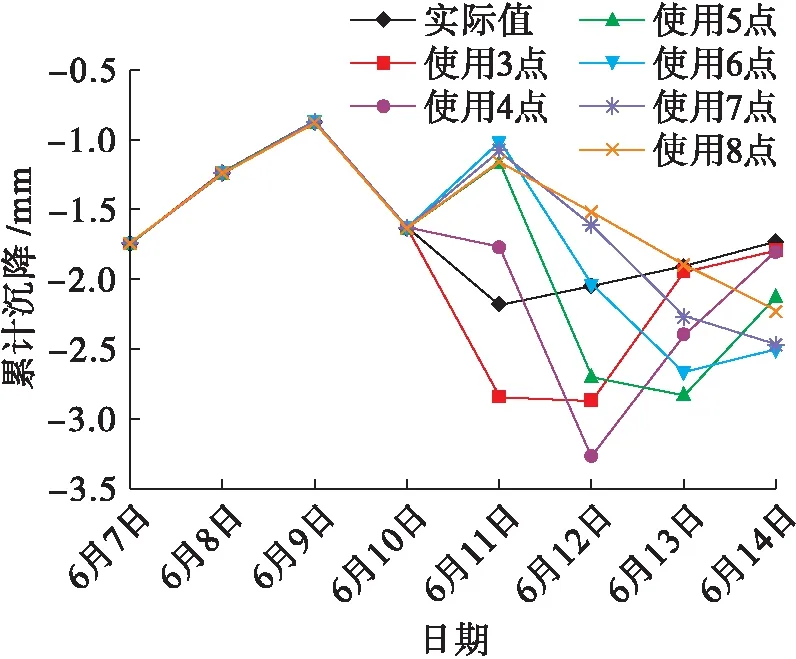
图5 6号点累计沉降实际值与预测值Fig.5 Measured and predicted values of cumulative settlement of point 6
灰色系统理论在处理小容量样本、贫信息、不确定系统方面有较强优势,原始序列较少时更能体现出灰色系统理论的优势,使用“新陈代谢”模型使预测模型更具有时效性,因此,在数据较少情况下平均误差相对较小.
2.2 原模型的优化
根据GM(1,1)模型的局限性,对模型的改进主要有两种方式:一种是改变原始序列的平顺度,使序列变得平顺从而减小预测;另一种是改变建立模型时的背景值Z(1)(k),从而提高预测精度.
根据上述思路对新陈代谢GM(1,1)模型进行改进,取原始序列的缓冲算子作为原始序列,然后构建新的模型,对累计沉降量进行预测,改变背景值的构造方法,使模型更加接近实际走势.
模型1当模型变化趋势不变时,预测值总比实际值大,取弱化缓冲算子比较合理,取平均弱化缓冲算子(AWBO)对原始序列进行处理,再根据前文方法建立新陈代谢GM(1,1)模型.AWBO的定义如下:
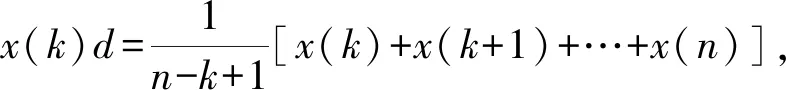
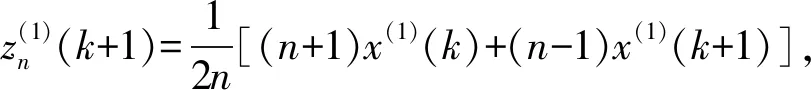
式中:N为原始序列长度;Ri=x(1)(i)/x(1)(i-1),i=2,3,,N.
模型3将上述两个模型进行整合,先按照模型1的方法得出缓冲算子序列并作为新的原始序列,再采用模型2中的方法构造背景值.
使用模型1~3分别对1号点进行预测分析,预测结果与误差如表4所示.
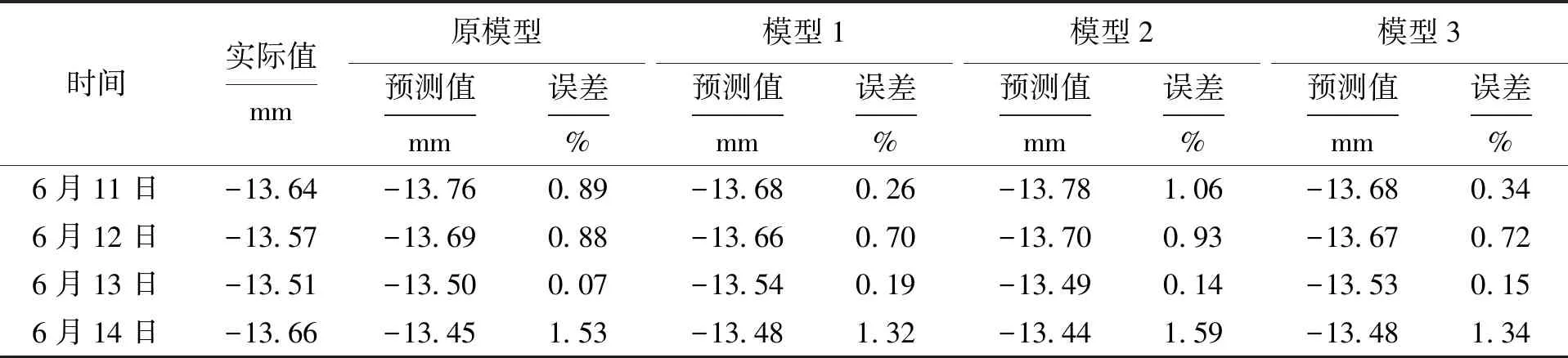
表4 各个模型对1号点的预测值及误差Tab.4 Predicted values and errors of point 1 in each model
表4中4种模型的平均相对误差分别为0.847%、0.616%、0.931%、0.641%,模型1的平均相对误差最小,其次是模型3,而模型2的误差比原模型的误差大.实际值与预测值如图6所示.表5为各个模型对2号点的预测值及误差.
表5中4种模型的平均相对误差分别为1.445%、1.196%、1.544%、1.183%,模型3的平均相对误差最小,其次是模型1,而模型2的误差比原模型的误差要大.实际值与预测值如图7所示.
通过分析各个模型对1号点、2号点累计沉降量的预测可知,背景值的改变并不能改变模型对地铁开挖时产生累计沉降量预测的精度,且相比对缓冲算子的影响,预测值的改变量要小得多.
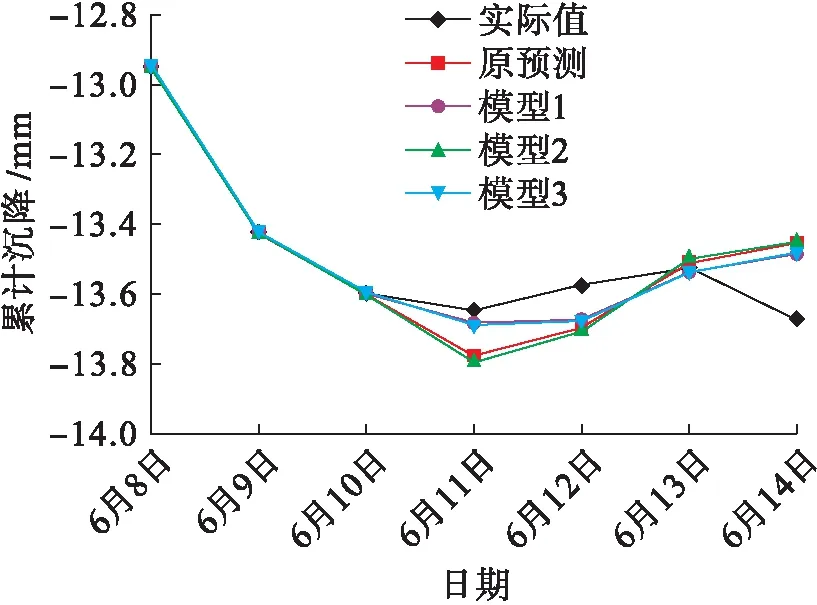
图6 模型优化后1号点累计沉降实际值与预测值Fig.6 Measured and predicted values of cumulative settlement of point 1 after model optimization
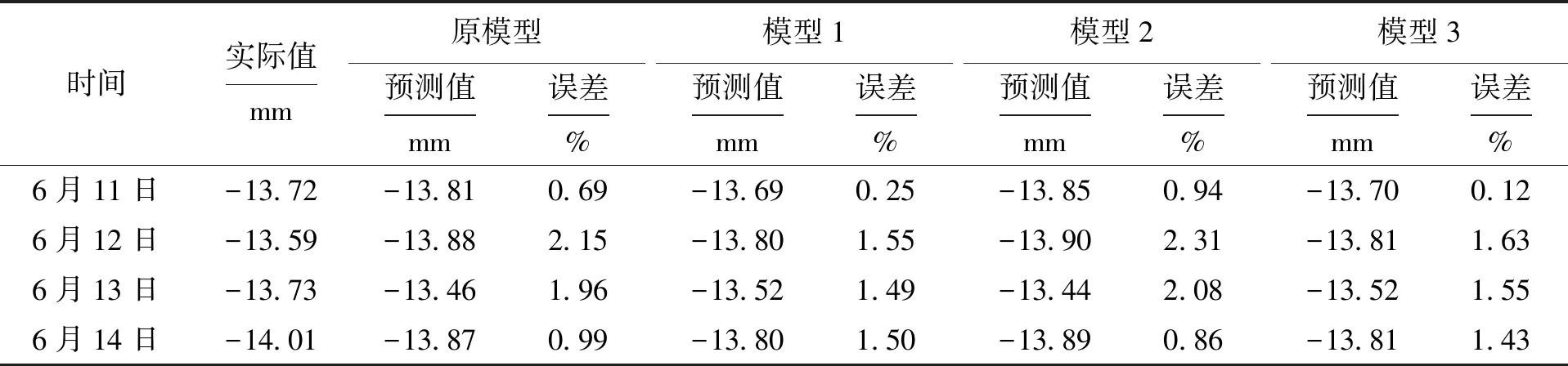
表5 各个模型对2号点的预测值及误差Tab.5 Predicted values and errors of point 2 in each model
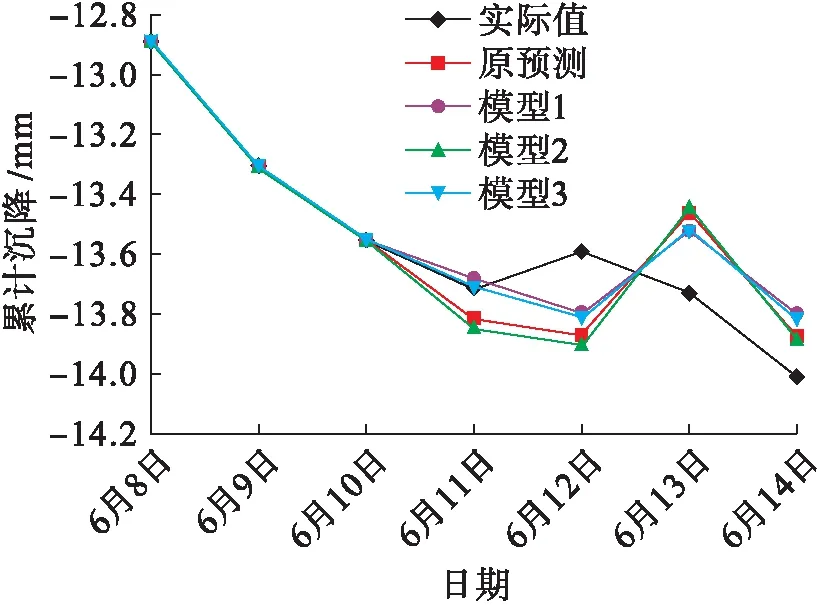
图7 模型优化后2号点累计沉降实际值与预测值Fig.7 Measured and predicted values of cumulative settlement of point 2 after model optimization
图8、9为5号点、6号点累计沉降实际值与预测值.对比分析各个模型对5号点和6号点的预测可知,当原始序列变化平顺时,各个模型的预测值相差不大,缓冲算子对提高测量精度作用不明显,甚至会使预测出现更大偏差.但当模型较为曲折时,模型1和模型3对预测精度的提高相当明显.通过以上分析可知,缓冲算子改进模型对不平顺原始序列的预测精度要高于原预测模型的精度,但对平顺原始序列的改进效果则不太明显.
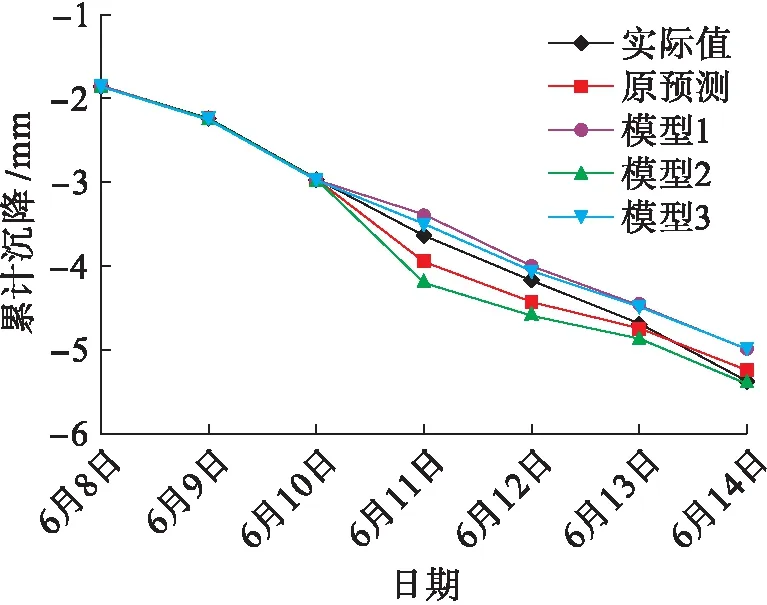
图8 模型优化后5号点累计沉降实际值与预测值Fig.8 Measured and predicted values of cumulative settlement of point 5 after model optimization
3 结 论
本文使用灰色系统理论对地铁暗挖区拱顶地表沉降量进行预测,并提出如下改进方法:
1) 对模型取用原始序列中数据个数进行了研究,对比取用3~8个数据时的预测精度,得出了最优取用个数.
2) 结合灰色模型本身局限性对新陈代谢GM(1,1)模型进行优化,通过对比分析可知,背景值优化对模型预测值影响较小;缓冲算子优化在原始序列变化较大、变化不平顺时优化较好,但如果原始序列变化平顺则其优化效果不好.

图9 模型优化后6号点累计沉降实际值与预测值Fig.9 Measured and predicted values of cumulative settlement of point 6 after model optimization
