各向异性介质中地震波参数反演及其在隧道不良地质预报中的应用

何现启，彭凌星，鲁光银，朱自强，高峰

(1.湖南省交通规划勘察设计院有限公司，湖南长沙，410200；2.中南大学地球科学与信息物理学院，湖南长沙，410083)

EDA(extensive dliatancy anisotropy)介质即具有一组定向排列的垂直裂隙的介质，也称广泛各向异性介质、裂隙扩容各向异性介质和方位各向异性介质。通过对EDA 介质的研究，可探明地层裂隙的分布和密度，进一步研究裂隙中充填物的性质，为灾害预报、地下水探测等提供重要资料。通过对地震波速度及其衰减进行分析还可以推断地下冷热水的运移和储存情况，从而评价地下水资源，预报地下工程突水、涌泥等地质灾害。地震波振幅随岩石物理性质的变化比地震波速度的变化更大，因此，地震波衰减可能比速度携带了更多的表征岩石物理性质的信息。在各向异性速度反演及走时研究方面，卢明辉等[1]采用小生境遗传算法，对3条成一定角度的测线走时信息进行速度和各向异性参数反演。杜启振等[2]对常规双曲线时距方程进行了改进，给出了VTI(vertical transverse isotropy)介质时距方程。在各向异性地震波衰减估计方面，BEHURA等[3]研究了VTI介质和正交各向异性介质中相衰减和群衰减的变化规律，并利用谱比法进行衰减估计；徐善辉等[4]通过PP 转换纵波和PS 转换横波的反射系数反演了各向异性参数和对称轴倾角、方位角等，提出了利用PS 波振幅定性分析TTI(titled transverse isotropy)介质对称轴倾角的方法。在射线追踪算法方面，李强等[5]系统综述了国内外不均匀介质中各种主要和实用的射线追踪方法。段鹏飞等[6]为了方便、快捷地实现TI(transverse isotropy)介质射线走时与局部角度的计算，讨论和对比了2种改进的射线追踪方法。曲英铭等[7]在Vidale 差分算式基础上推导出不规则网格差分算式，是适用于不同网格剖分方式的有限差分走时计算方法。王东鹤等[8]分析了各种算法的研究现状，并对射线追踪法的发展趋势进行了展望。韩松[9]通过1.2D 和3D 的快速扫描法计算了TTI介质中qP 波的走时，并通过新型快速扫描法(fast scanning method,FSM)，得到走时。欧阳进[10]采用射线方法对复杂的地质模型进行了波场正演。HE 等[11]指出含裂缝介质不仅具有速度各向异性，而且具有显著的衰减各向异性，衰减各向异性分析方法可应用于裂隙产状、裂隙密度和发育范围等的估计。居兴国等[12]在程函方程法射线追踪的基础上，提出了基于相速度的TTI介质射线追踪新策略。刘瑞合等[13]采用PSV 波分离的射线追踪方法，为层析反演提供了准确的旅行时和射线路径等信息。龚屹等[14]对采用射线追踪方法得到的微地震事件走时正演值与实际走时进行了对比分析。张敏等[15]通过对运动学和动力学追踪方程进行了修改和简化，有效地提高了各向异性介质射线追踪算法的计算效率。洪启宇等[16]指出利用2个相互正交的变井源距垂直地震剖面(walkaway vertical seismic profiling)可以完全确定钻井中TTI 介质qP 波的3 个WA(weak anisotropic)参数和对称轴的2 个方向参数。葛子建等[17]基于贝叶斯反演框架建立了P波线性AVAZ(amplitwde versus angle and azimuth)反演方法。国内外研究者在各向异性介质参数反演方面也进行了大量研究，如RUSMANUGROHO等[18]发现Voigt和Tromp参数能快速、稳定地反演陡峭倾斜的背斜结构。XU 等[19]建立了相似性分析框架用以反演最佳各向异性参数。LU 等[20]为了增强反演结果，采用层次反演策略来解决Gauss-Newton 方法中的局部最小解问题，并分别在理想和噪声的情况下对合成数据进行了测试，发现该方法可以成功识别复杂岩性和流体信息。BOITZ 等[21]研究了横向各向同性(VTI)介质的2种不同效应，即源的各向异性和传播路径上的各向异性，并用效能张量乘以具有等效剪切模量的各向同性弹性张量，来探明与岩石各向异性无关的构造变形情况。HADDEN 等[22]开发了一种各向异性波形断层扫描(anisotropic wave tomographe,AWT)方法，利用声学近似来模拟VTI介质中的地震波，并将这种方法应用于交叉井数据处理，在应用于加拿大西部沉积环境中的井间数据处理中具有很高的分辨率。人们对地震各向异性进行了大量研究，但将相关方法用于裂隙范围探测、地下水预测及误差分析尤其是隧道富水区等地质灾害探测的研究很少。为此，本文作者在研究弹性HTI(horizontal transverse isotropy)的基础上，研究黏弹性EDA 介质地震波速度分析算法并对各向异性参数、裂隙方位、裂隙密度等参数进行反演，对反演误差及其影响因素进行分析。

1 EDA 介质中倾斜界面的动校正速度及时距方程

1.1 方位垂直裂隙(EDA)介质中倾斜界面的动校正速度

由HTI介质精确动校正速度表达式，经坐标旋转可得到垂直非均匀EDA 介质中倾斜界面的精确动校正速度[23-25]：

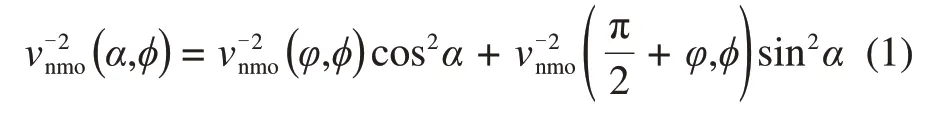
式中：α为共中心点排列的方位角；φ为EDA介质的对称轴的方位角；ϕ为对称轴倾角；vnmo为动校正速度。

在弱各向异性介质中，同理可得沿界面倾向的P波的动校正速度为[25]

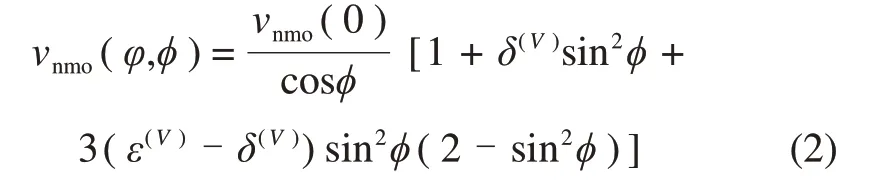
由式(2)可知动校正速度vnmo(φ,ϕ)主要由垂直各向异性参数ε(V)与δ(V)的差值和水平界面的动校正速度vnmo(0)决定。由HTI介质中的动校正公式，经坐标旋转同样可得沿界面走向的动校正速度vnmo((π/2)+φ,ϕ)为

1.2 对称面内P波动校正速度与射线参数的关系

由HTI 介质中射线动校正速度推导[25]，EDA 介质中沿界面倾向的动校正速度可用射线参数表示为

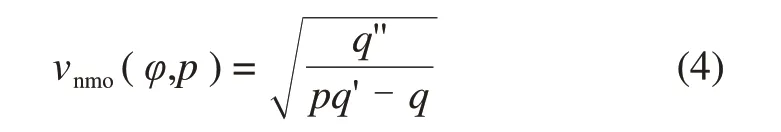
式中：q'为一阶导数；q''为二阶导数；p为慢度向量的水平分量；q为慢度向量的垂直分量，

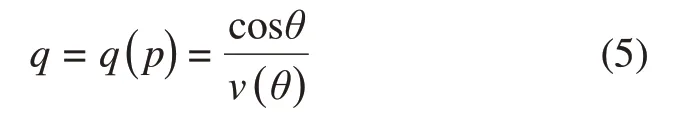
式中：θ=α-φ。

沿界面走向的动校正速度可用射线参数表示为

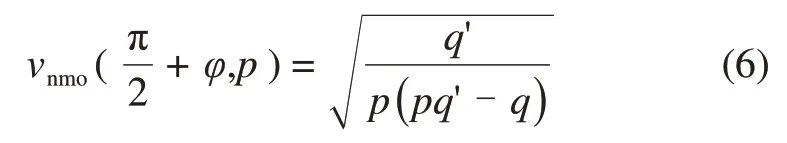
与HTI介质一样，所有的参数都为零偏移距射线参数。动校正速度与射线参数的关系都隐藏在慢度向量分量和其微商中，为确定动校正系数，便于反演计算，下面主要讨论动校正速度与射线参数的显性关系。

2 EDA 介质中三维动校正速度与射线参数的关系

2.1 均匀EDA介质中用射线参数表示的动校正速度精确表达式

由动校正速度和慢度向量及2层介质中的时距方程可得[24-25]

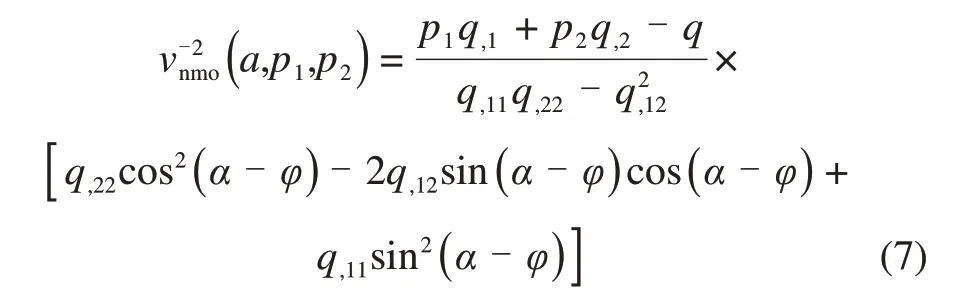
式(7)对所有的非转换波都成立，其中p1和p2分别为零偏移距射线在x和y方向的2 个水平慢度向量分量，垂直慢度向量分量q=p3，也可由Christoffel方程计算。

2.2 弱各向异性EDA介质中对称面内射线参数与动校正速度的关系

EDA 介质可由HTI 介质绕z旋转角度φ得到，对垂直方向的参数没有影响，因此，计算EDA 介质的垂直慢度仍可采用HTI介质中的计算公式。

将垂直慢度q用η(V)表示，并将q及其微商代入动校正方程(7)并用各向异性参数进一步线性化，可得到弱各向异性EDA介质中P波的近似动校正速度：

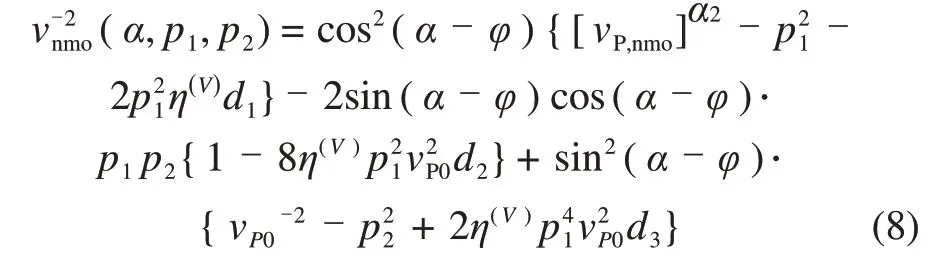
其中：vP0为纵波速度；

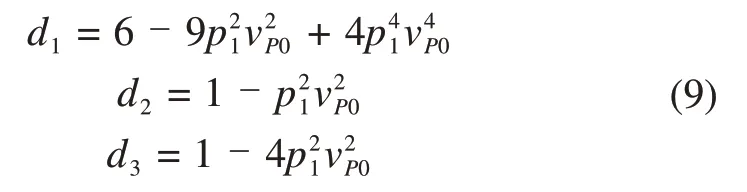
假设倾斜方位与介质对称轴重合,可得界面(α=φ)的倾斜面上的动校正速度为[22]

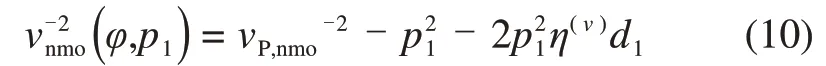
若用代替vP,nmo，EDA 介质中的η(V)和分别与HTI介质中的η(V)和相等，则式(10)与HTI介质中沿倾向的P波动校正速度的弱各向异性近似表达式一样，vnmo(φ,p1)可由HTI 介质中公式计算。若界面的倾向与各向同性面重合，走向与对称面平行，则[22]

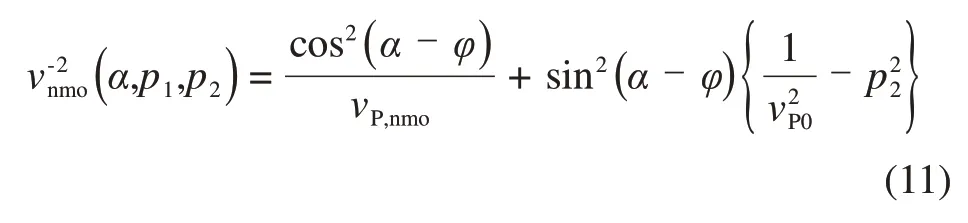
3 层状EDA 介质中倾斜界面的似Dix公式

在倾斜EDA 介质中，对动校正速度除考虑其测线方位角外，还要考虑倾角的影响。综合分析HTI介质对称面内的动校正速度公式以及其与坐标轴的相互关系，采用剥层法由相似分析得到[22]：

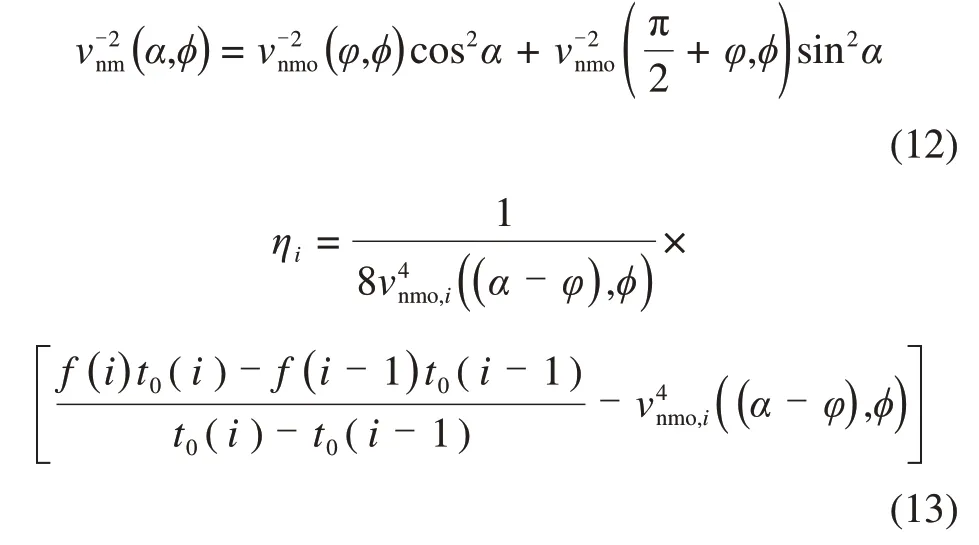
也可用下式计算：

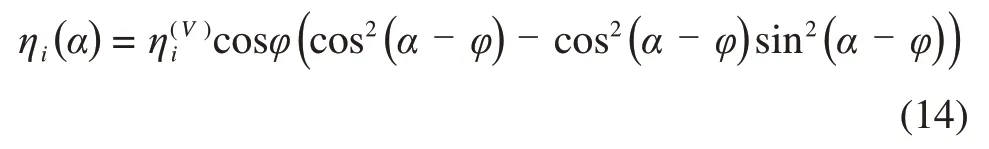
其中：f(i)为第i层界面反射波振幅；t0(i)为第i层界面反射波走时。由式(12)，(13)和(14)即可得到其相关的等效速度和地层速度。

4 EDA介质中的P波参数反演算法

对于1个给定的垂直时间t0，通过对水平速度vhor和动校正速度vnmo进行二维相似分析可以得到1 个具有最大相似值的模型，相似系数可由下式计算：

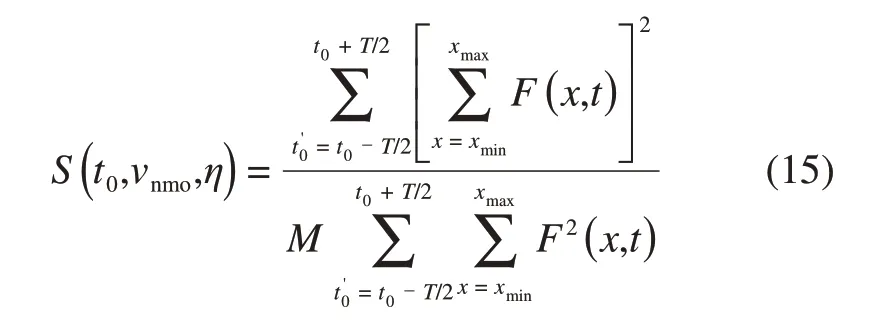
其中：M为道数。反射波振幅F(x,t)以及其平方F2(x,t)都是沿着时距曲线t(t'0,vnmo,x)计算的(其中双曲线的顶点位于垂直走时t'0处，t'0在以时间t0为中心的平移窗口内)。2 个采样时间间隔之间的反射波振幅F(x,t)可通过线性插值进行计算。

通过对多个排列进行速度分析即可确定动校正椭圆，由动校正速度与各向异性参数的关系式即可计算出各向异性参数[25]。

所采用的目标函数如下：

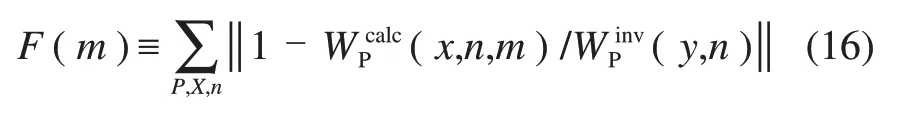
其中：(x,n,m)为模型计算速度；(y,n)为数据反演所得速度；x和y为坐标轴；m为模型参数。采用最小二乘法计算最佳层参数。

反射界面可用多项式表示，主要参数为节点数、节点处界面的法向量及x和y方向多项式的维数。其中，界面法向分量与射线参数的垂直分量一致，由基于拟牛顿法的最优化射线追踪法确定界面最佳几何参数。

5 模型算例分析

5.1 地层模型

模型参数见表1，模型1示意图见图1。其中，第1层界面倾斜10°，第2层和第3层倾斜20°，上面3层为EDA介质，下面2层为VTI介质。

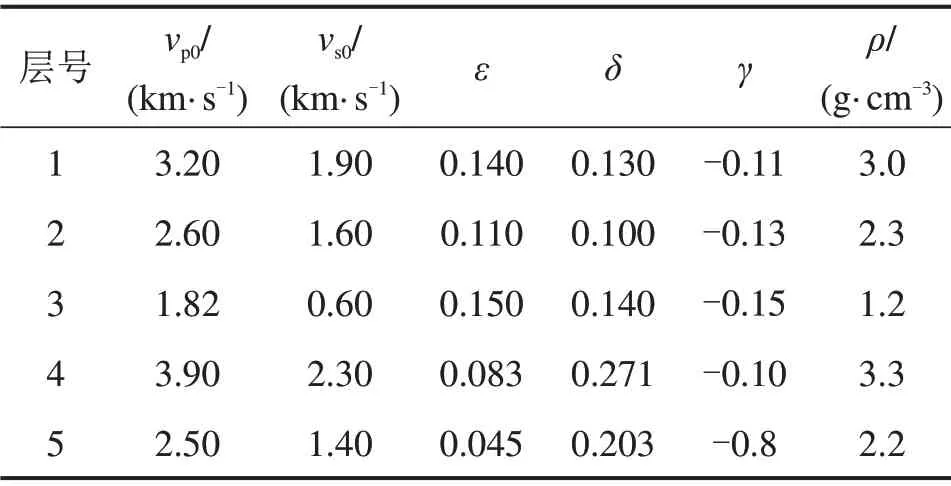
表1 模型1 弹性参数Table1 Elastic parameter of Model 1

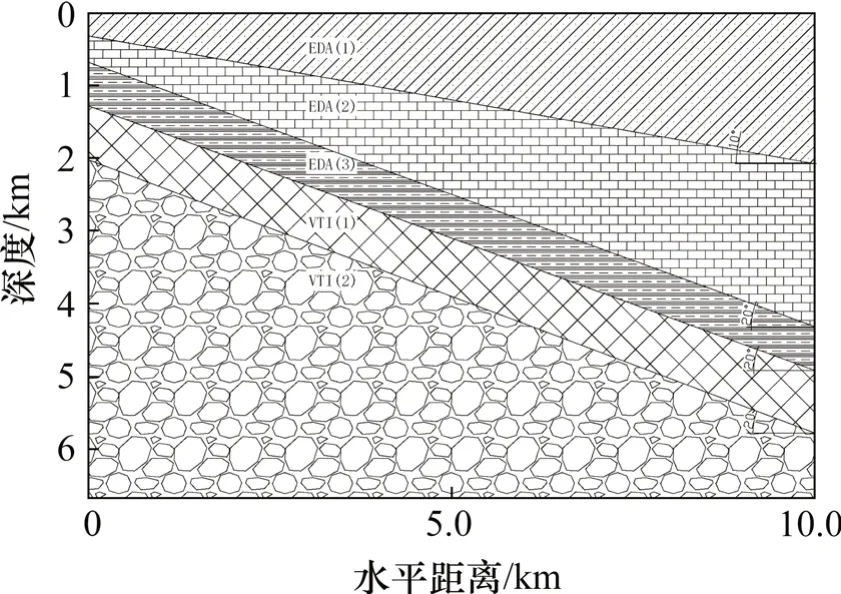
图1 模型1示意图Fig.1 Schematic diagram of model 1

用黏弹性实射线追踪法实现黏弹性EDA 中地震波的数值模拟，模拟地震波形见图2。

5.2 速度分析

采用式(16)对速度进行分析，结果见图3。从图3可以看出：0°测线的叠加速度显示反演结果与模型值基本一致，相对误差在5%以内，动校正结果显示的界面层数及界面产状与实际情况相符；同时，0°，10°，20°和30°测线的叠加速度和动校正速度结果均与实际情况一致，说明速度及动校正公式计算结果准确度高。

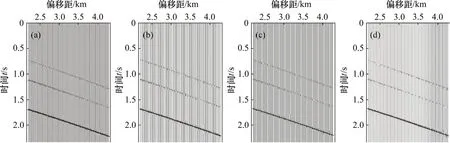
图2 模型1 不同方位角的模拟地震波形Fig.2 Synthetic wave shapes of spreads with different azimuth angles for Model 1

图3 0°测线的叠加速度和动校正速度Fig.3 Stack velocity and NMO velocity for spread with azimuth angle φ=0°

5.3 反演结果与误差分析

5.3.1 无噪声反演及误差分析

未添加噪声的反演界面深度及倾角见图4。由图4可知：界面的反射倾角及方位与实际模型的基本一致，倾角误差在3°以内，方位角反演误差在5°以内。

其他相关参数反演结果见图5～7，其中，实线表示参数的精确值，黑点表示反演值。从图5～7 可见：迭代300次时，计算精度较高收敛较快，误差分析结果显示除方位角误差稍大外，其余参数相对误差都非常小，均在5%以内。

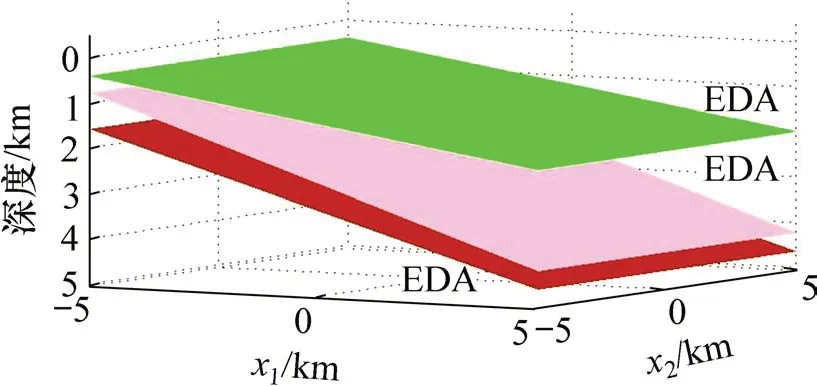
图4 未加噪声的模型几何参数反演结果Fig.4 Inversion results of geometric parameter of reflectors without noise

从图5可见：弹性介质各向异性参数ε及纵波速度反演计算精度较高，收敛较快，各层参数的反演值均集中在实线附近，误差分析结果显示相对误差在5%以内。

从图6可见：对第1 层介质方位角反演计算精度较高，收敛较快，对第2层和第3层介质的反演值相对较离散，个别反演值相对误差较大。

从图7可见：对第1 层和第2 层介质密度反演计算精度较高、收敛较快，对第3层介质的反演值较离散，但反演值均集中在实线附近，相对误差都在5%以内。

5.3.2 带噪声反演成果及误差分析

在反演中加入高斯噪声，加噪后反演的介质模型见图8，反演结果见图9～12。从图9～12 可以看出：加入噪声后对反演的速度和精度影响较大，其中各向异性参数ε和裂隙方位的收敛速度和精度较低，第3层的裂隙方位角反演相对误差最大达10%。其余反演结果相对误差均匀在5%以内。

从图8可见：加入高斯噪声后，反演的地层界面倾角均与实际模型的基本一致，噪声对反演的结果影响较小，可忽略。

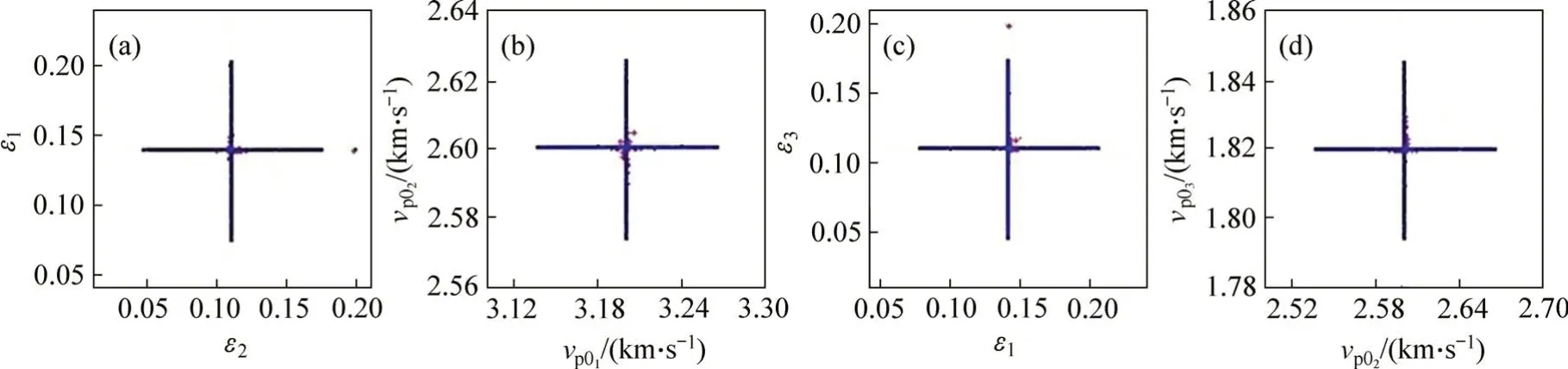
图5 各向异性ε及纵波速度反演结果Fig.5 Inversion results of ε and P wave velocity

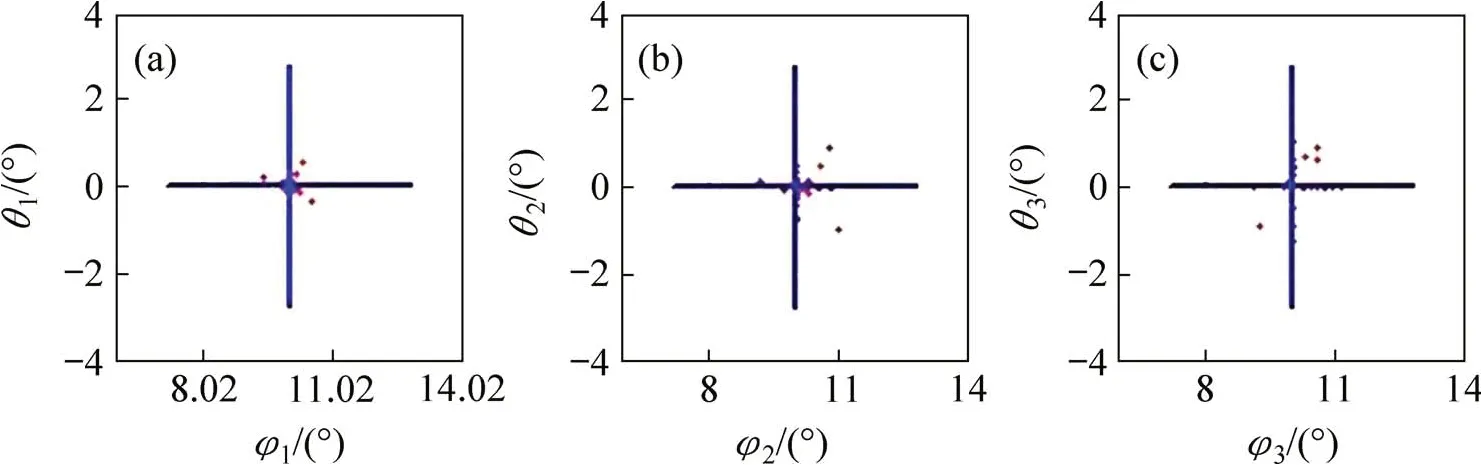
图6 裂隙方位角反演结果Fig.6 Inversion results of azimuth angle of fracture

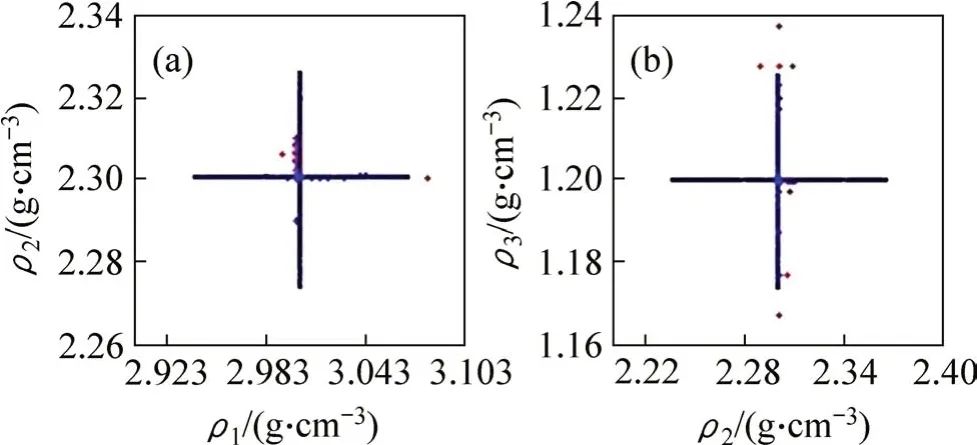
图7 密度反演结果Fig.7 Inversion results of density

从图9可见：加入高斯噪声后，ε反演结果较离散，速度反演值在实线附近，相对误差在8%以内。

从图10可见：第1层介质的方位角反演值在实线附近，相对误差在5%以内；第2 层介质反演相对误差在8%以内；第3 层介质反演结果较离散，反演误差较大。

从图11可见：第1层和第2层介质的密度反演值均在实线附近，相对误差在8%以内；第3 层密度反演较离散，反演相对误差较大。从图12可见：第1，2和3层介质的各向异性参数δ反演值均在实线附近，反演相对误差在8%以内。

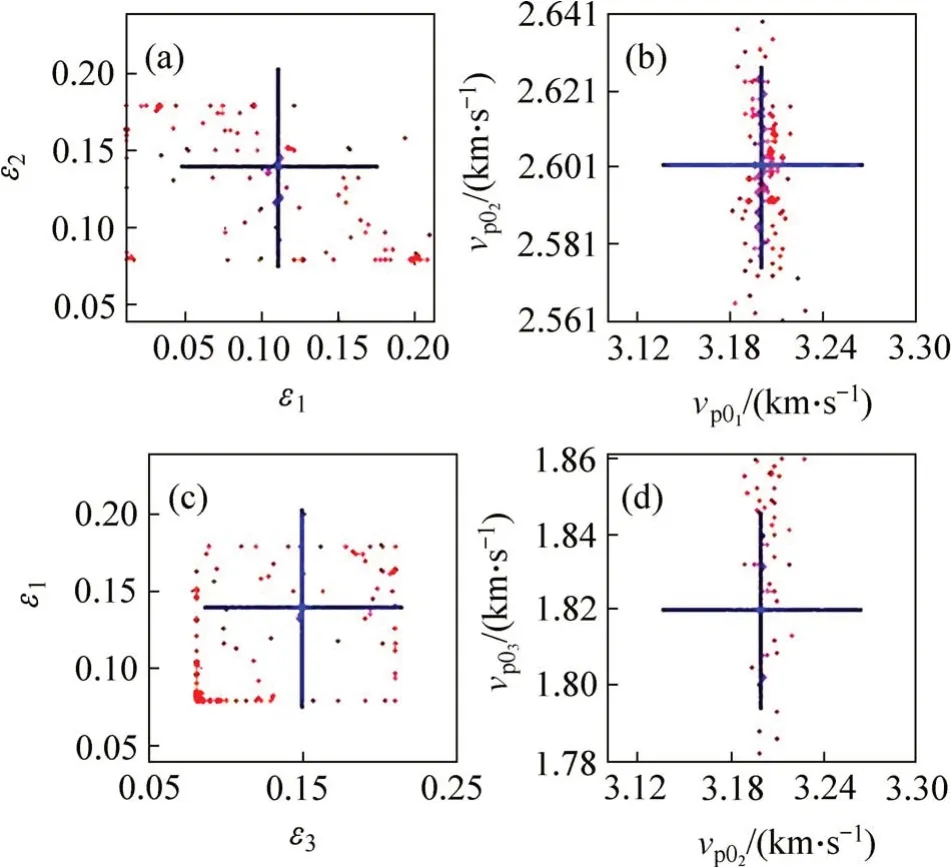
图9 ε及纵波速度反演结果Fig.9 Inversion results of ε and P wave velocity

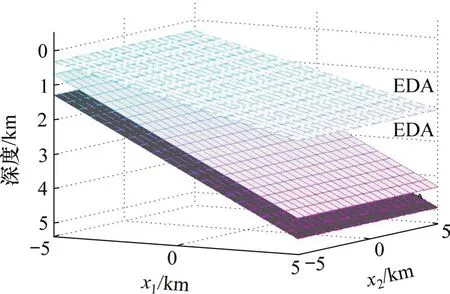
图8 加噪后反演的介质模型几何参数Fig.8 Inversion results for geometric parameter of reflectors adding gauss noise

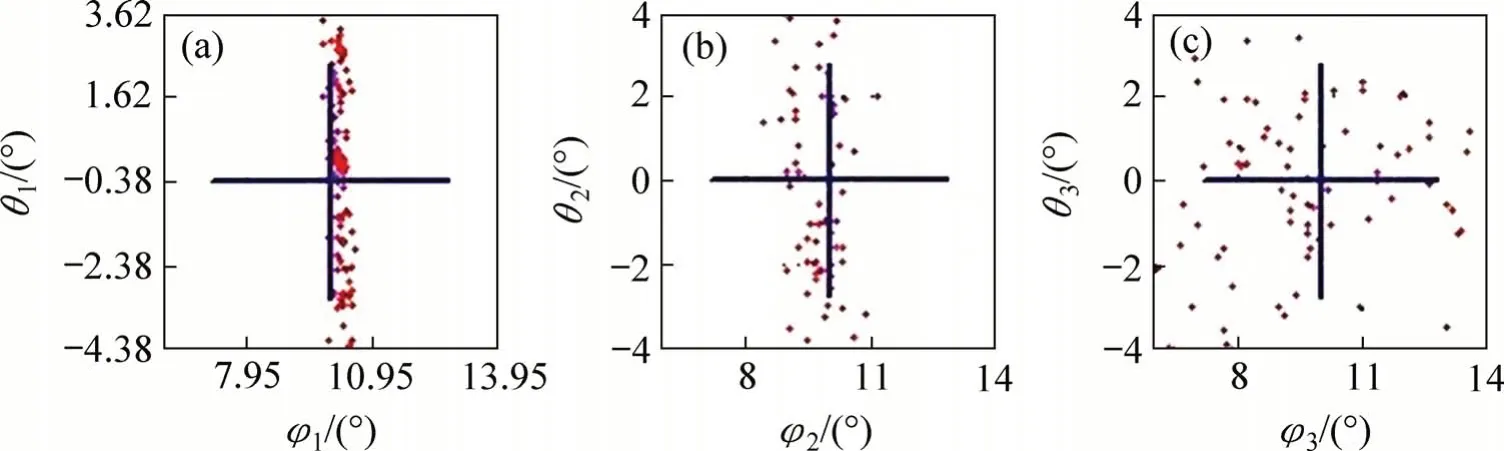
图10 裂隙方位角反演结果Fig.10 Inversion results of azimuth angle of fracture

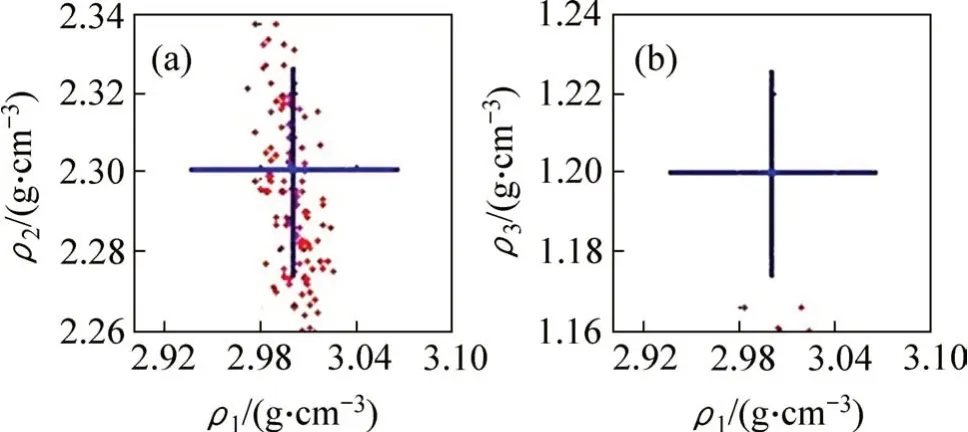
图11 密度反演结果Fig.11 Inversion results of density

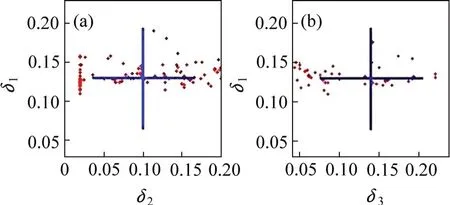
图12 各向异性参数δ反演结果Fig.12 Inversion results of anisotropy parameter δ

6 工程实例

为了验证该方法的可行性，将其应用于裂隙发育区及富水区预报。通过现场测试，分析地层裂隙走向、节理密度与速度分布的关系，研究地震波速度及衰减与地下水赋存状态的关系。

6.1 现场测试概况

测区桩号为K74+650—YK74+900，隧道走向约340°。依据洞内开挖情况，地下岩体垂直向裂隙极其发育，地下水极其丰富，为了探明掌子面前方地质情况，在地面上共布置4条不同方位的测线，采集广角反射法地震勘探数据，测线布置如图13所示。沿隧道的轴线建立采集坐标系，沿轴线设为x，正方向指向大里程。为确保测线为长排列，依据隧道埋深确定测线长度大于270 m，实际测线长度为360 m，测线2采集地震波数据如图14所示。

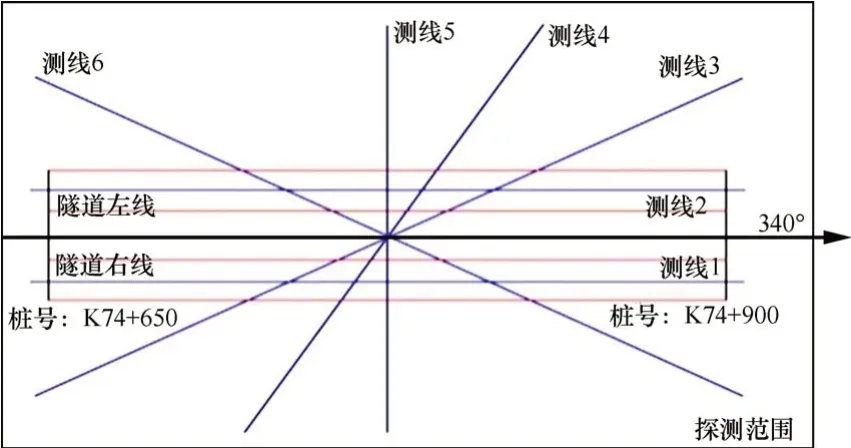
图13 测线布置图Fig.13 Schematic diagram of spreads distribution

6.2 数据分析

经速度分析得动校正速度，如图15所示。从图15可见动校正速度与方位角的关系可近似为1 个椭圆，长轴方向约为335°，由此可见主要裂隙走向约为335°。

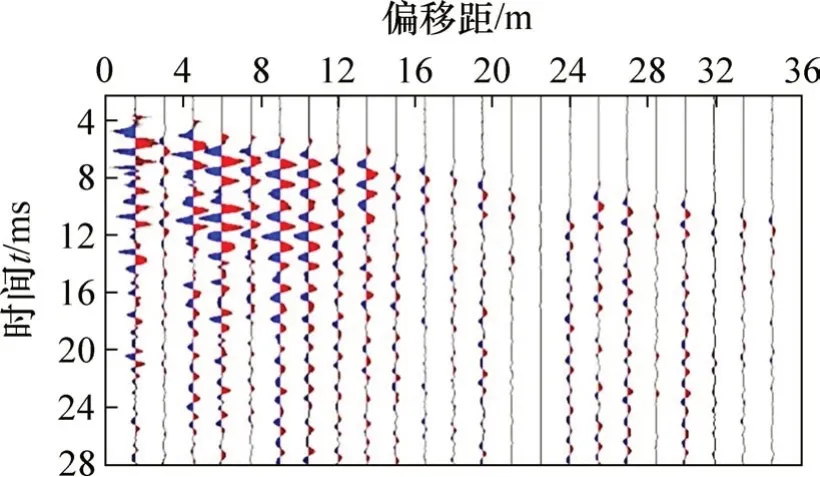
图14 测线2地震波数据Fig.14 Seismic data for spread 2

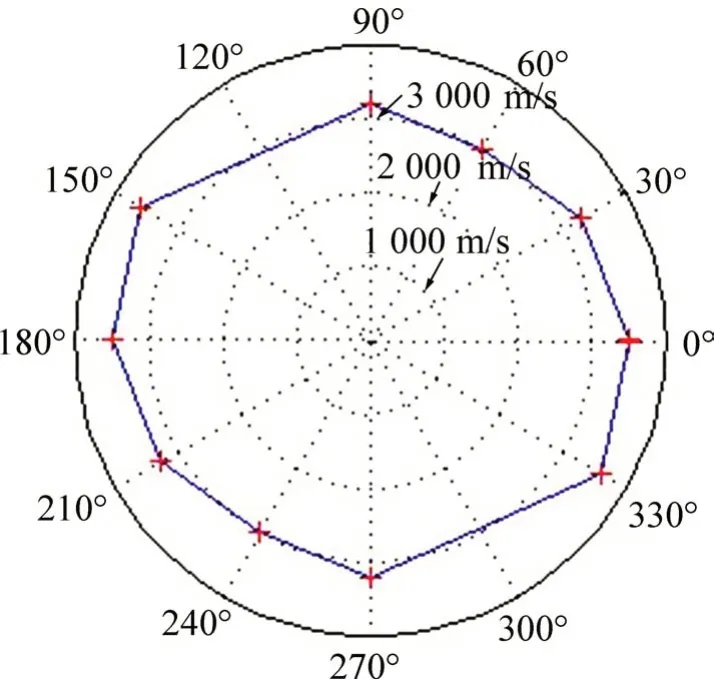
图15 不同方位测线的动校正速度Fig.15 NMO velocity for spreads of different azimuths

图16和图17所示分别为测线2 的速度谱和衰减谱。分析图16和图17可知：在深度40～65 m处存在1 个高速度带，此时衰减较弱；在65～120 m 时，虽然速度相对地表仍然较高，但其衰减系数较大，地震波衰减较快，由此推测K74+650—K74+900 范围内，深65～120 m处地下水较丰富。随后的隧道开挖结果证明地下水极其丰富，主要裂隙走向约为330°，反演结果与之相差5°左右。

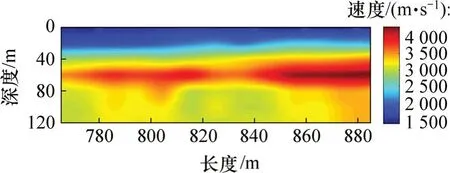
图16 测线2速度谱Fig.16 Velocity spectral of spread 2

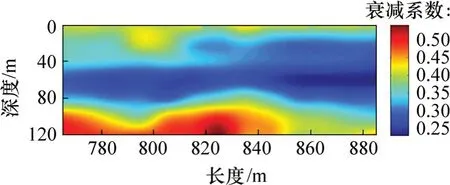
图17 测线2衰减谱Fig.17 Attenuation spectral for spread 2

7 结论

1)以HTI 介质为基础，通过坐标旋转得到了EDA 裂隙诱导介质中地震波的三维动校正速度表达式和走时方程。以HTI介质中的动校正速度、慢度向量及走时方程为基础，推导出动校正速度的射线参数表达式。利用最小二乘法对模拟记录进行非双曲时差分析，得到动校正速度，然后由动校正速度与各向异性参数及对称轴方位角的关系式进行参数反演。

2)通过对广角数据进行速度分析得到动校正速度，采用射线追踪及多项式拟合法可确定多层倾斜地层界面；由地震波走时及射线追踪法，利用多项式拟合法可反演多层倾斜裂隙地层的界面几何参数。

3)反演速度与理论计算速度相对误差小于5%；据各向异性参数反演可确定EDA 介质的裂隙发育方位。裂隙介质参数反演的相对误差均在5%以内；加入高斯噪声后，裂隙方位角和各向异性参数ε相对误差均在10%以内，其他相对误差均在5%以内。

4)速度谱反映的地质情况与衰减分析结果一致，裂隙走向反演结果相对误差为5°。所提出的反演方法可应用于隧道裂隙发育及富水区预报，具有较高的预报精度。