高频冲击中心孔岩石损伤模型及试验研究
2019-09-18吴万荣姚壵刘智
吴万荣,姚壵,刘智
(中南大学机电学院,湖南长沙,410083)
在大型硬岩矿山开采中,常采用冲击钻孔或牙轮碾压切削钻孔。然而这些钻孔工艺方法在进行硬岩大直径深孔作业时,存在效率较低、钻齿磨损严重等问题。针对这些问题,娄磊等[1]提出了一种冲击诱导切削复合破岩的钻孔工艺。采用冲击钻头高频冲击钻凿中心孔,围岩会在冲击扰动载荷的影响下产生裂纹损伤,削弱围岩强度;采用牙轮钻头对损伤区域进行切削,从而提高钻孔的效率,降低钻孔能耗,减少钻头磨损。复合破岩最终钻孔孔径、钻头切削能耗与效率受到冲击中心孔周围岩石损伤区域及损伤程度的影响,损伤区域范围及损伤程度又受到冲击中心孔半径的影响。为了确定复合破岩钻孔工艺参数,需要研究冲击中心孔半径对围岩损伤的影响;而提高破岩效率、降低破岩能耗也涉及到隧道开挖、河道水坝开挖、基础工程等方面[2]。MEGLIS 等[3]应用超声层析成像对隧道开挖的围岩损伤进行现场测试,得到围压损伤程度和损伤分布规律。LU 等[4]在考虑轴向原岩应力影响的条件下,对圆形隧道开挖进行了弹塑性分析。朱晶晶等[5-6]通过改进的霍普金森压杆(SHPB)装置,对岩石在不同冲击载荷下的力学及损伤特性进行了研究。林大能等[7]通过循环冲击试验分析了损伤与围压、冲击载荷以及冲击次数之间的关系[7]。陈乐求等[8]研究了初始损伤对岩石抗压力学性质的影响。周辉等[9-10]基于岩石统一能量屈服准则和最小耗能原理建立了损伤本构模型。马念杰等[11-12]分别对圆形巷道围岩塑性区分布规律以及一般形态进行了研究。由于复合破岩适用于硬质矿山开采,因此,本文作者以质地坚硬、分布广泛、常用于试验研究的花岗岩为研究对象,采用电锤模拟冲击钻头对试样进行高频冲击,再采用SHPB装置对高频冲击中心孔后的试样进行试验研究。在此基础上,基于Weibull 分布建立适用于高频冲击中心孔试样的损伤本构模型,对不同冲击中心孔半径的损伤程度及损伤区域分布规律进行研究,以期为复合破岩钻具的结构设计以及高效、节能地进行硬岩大直径深孔采矿工程作业提供参考。
1 高频冲击中心孔损伤区域分析
冲击钻头在轴向力的作用下,不断向前推进,经过一段时间后,岩石在冲击钻头作用下,便逐渐卸荷为0。钻头冲击岩石的应力状态可近似看作布西涅斯克问题[13],在冲击载荷P的作用下,冲击中心孔壁(r=r0,其中r0为中心孔半径,r为径向半径)处的径向应力为
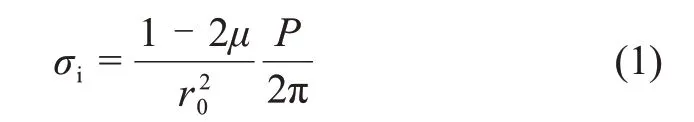
式中:μ为泊松比;σi为中心孔壁处的径向应力;r0为中心孔半径;r为径向半径。
1.1 弹塑性区应力分析
塑 性 区(r0<r≤r1)满足岩石塑性条件Mohr-Coulomb塑性准则[14-15]:
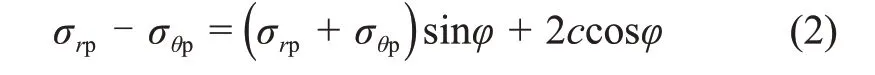
式中:c和φ分别为内聚力和内摩擦角;σrp与σθp分别为塑性区径向与切向应力;r1为塑性区半径。在围岩塑性区取一微分体abcd进行受力分析,如图1所示。图中,σr为微分体径向应力,σθ为微分体切向应力,τθr和τrθ分别为沿径向和切向的剪应力。
根据单元体径向和切向受力平衡可得
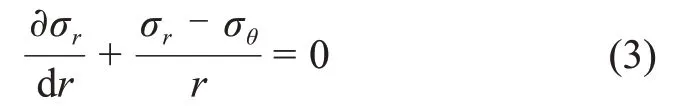
式(3)为轴对称条件下的应力平衡方程。联立式(2)和(3),根据边界条件可得塑性区应力为:
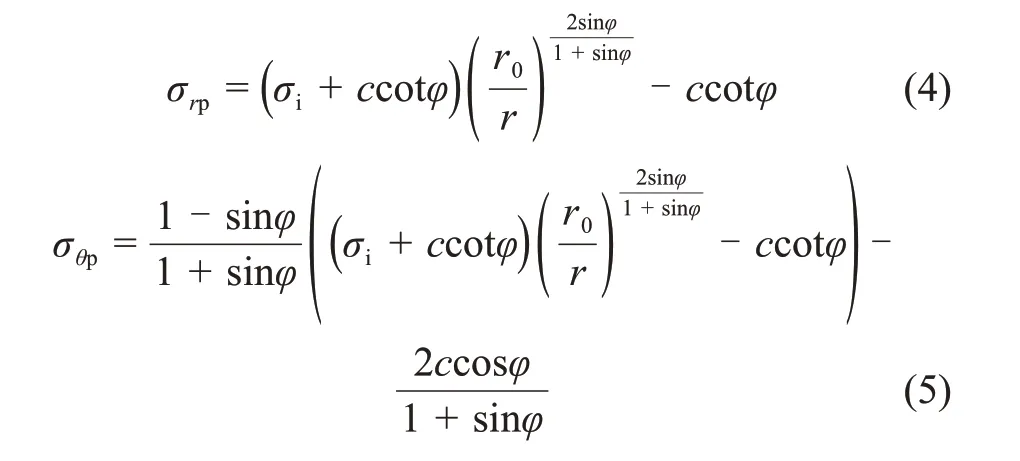
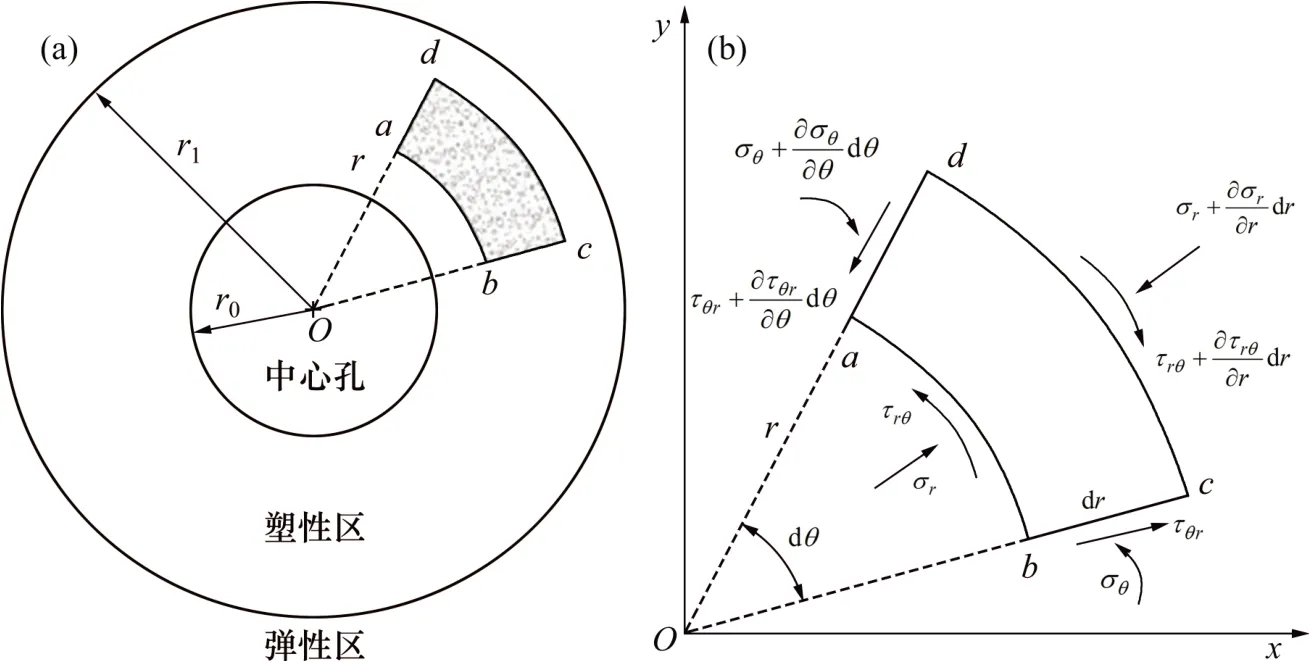
图1 围岩塑性区微元应力分析Fig.1 Stress analysis of micro-element in plastic zone of surrounding rock
对于弹性区,假设原岩应力为σ0,弹塑性区交界处的径向应力为σr1,则围岩弹性区(r1≤r)的应力[16]为
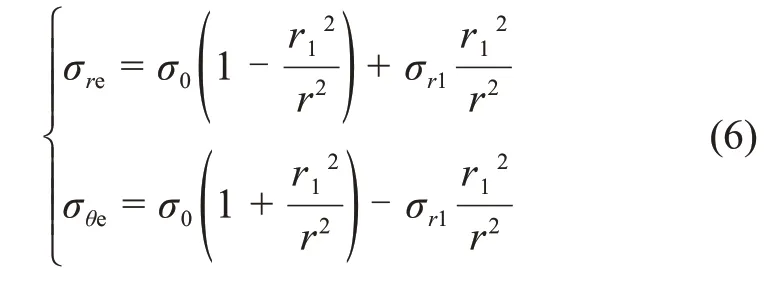
式中:σre与σθe分别为弹性区径向与切向应力。
1.2 冲击损伤半径及变形分析
弹性区应力和与塑性区应力之和分别为:
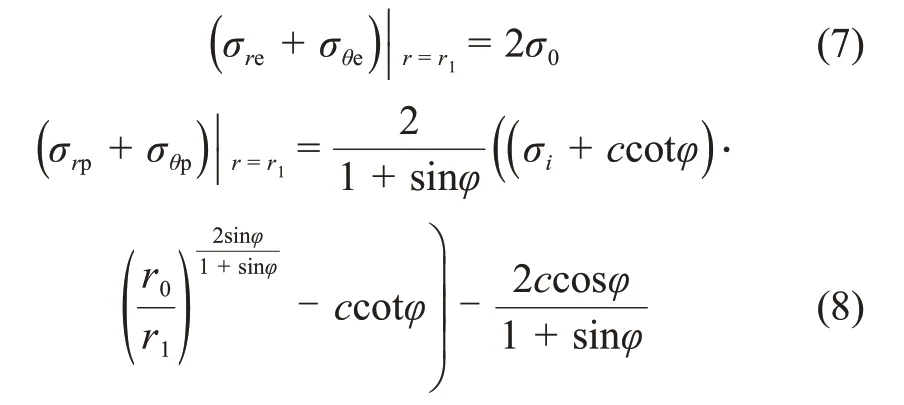
弹塑性交界处径向应力和与切向应力之和相等[17],则有

由式(9)即可求出塑性区半径r1。
总应变包含可恢复的弹性应变与不可恢复的应变,根据弹塑性理论,围岩塑性区总应变为
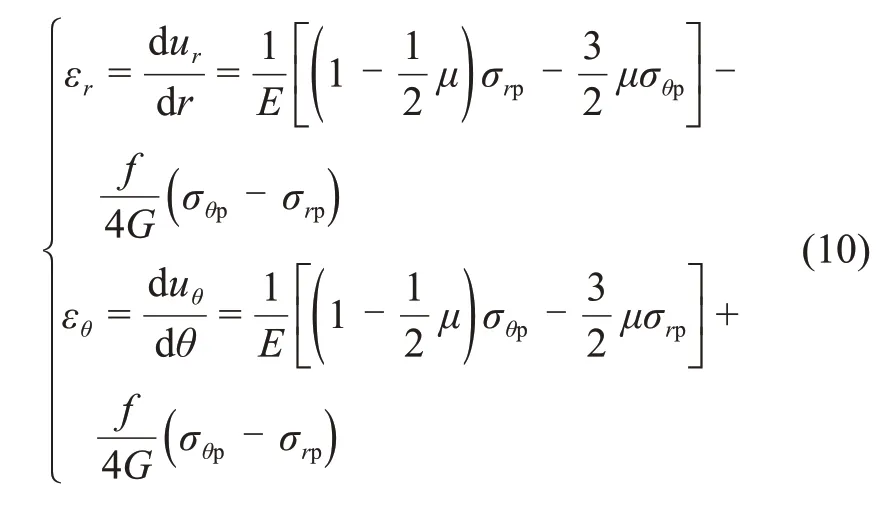
式中:E和G分别为弹性模量和剪切模量;ur和uθ分别为塑性区径向与切向变形;f为塑性函数,弹性变形阶段f=0。由式(10)可知体应变εv为
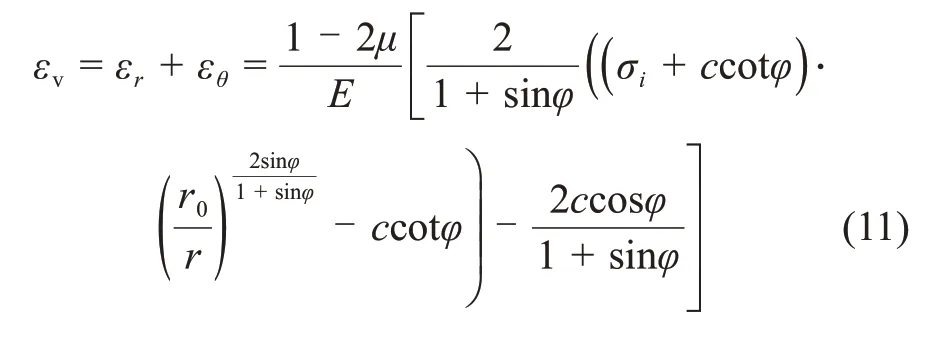
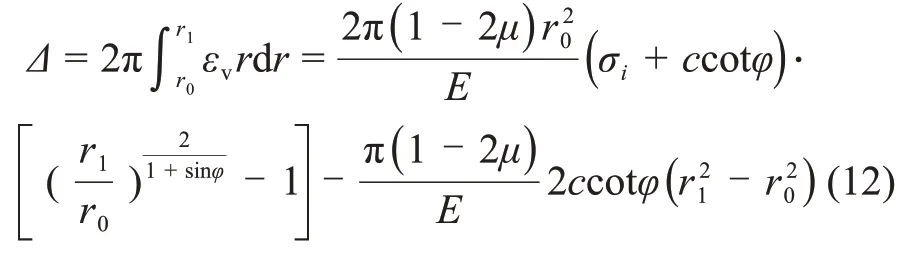
对式(11)积分,可得塑性区总变形Δ为则由损伤面积定义的钻头冲击产生的围岩损伤D0为
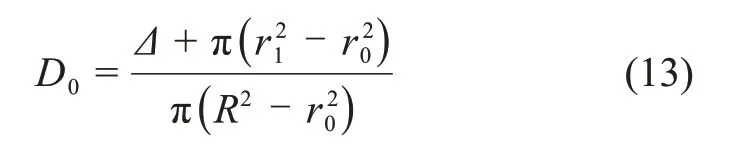
式中:R为试样半径。
2 高频冲击中心孔损伤本构模型
2.1 损伤本构模型的建立
损伤体服从Weibull 损伤分布[18-19]规律,概率密度函数p(F)的表达式为
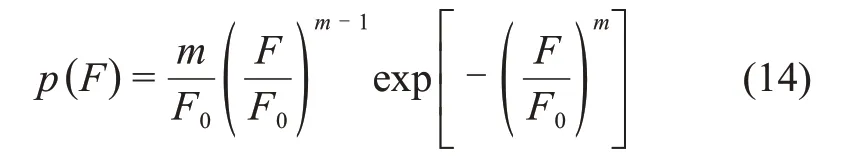
式中:F为微元体破坏强度的分布变量;m和F0为Weibull 分布参数,反映岩石材料的力学性质。统计损伤变量D为
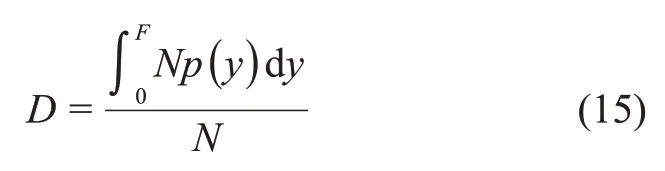
式中:N为总微元数。联立式(14)和(15)得
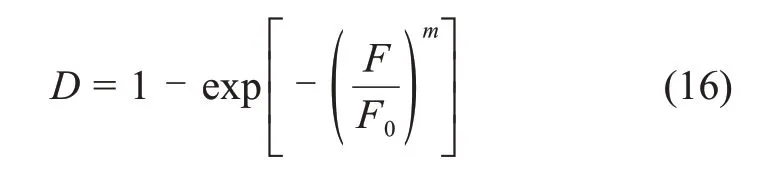
由式(16)可知:损伤变量与岩石微元体强度有关。考虑到Drucker-Prager 破坏准则具有参数形式简单、在岩石材料中应用广泛等优点,基于Drucker-Prager破坏准则的岩石微元强度为
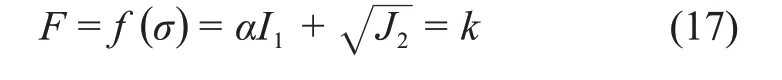
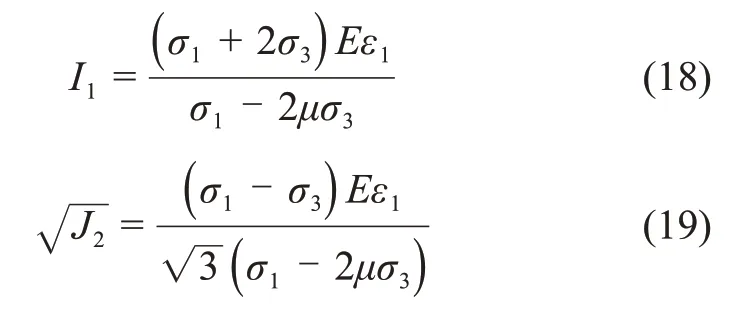
式中:σ1和σ3分别为最大和最小主应力,ε1为主应变。
在没有围压的情况即一维应力状态下,有σ2=σ3= 0,ε1=ε(ε为试样沿轴向加压方向的应变)。此时,联立式(17)~(19)得
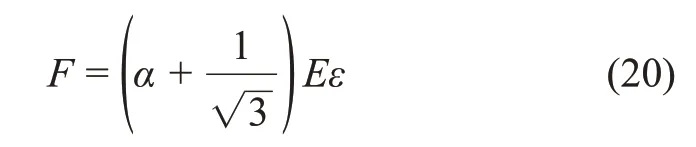
则高频冲击中心孔岩石的损伤本构方程为
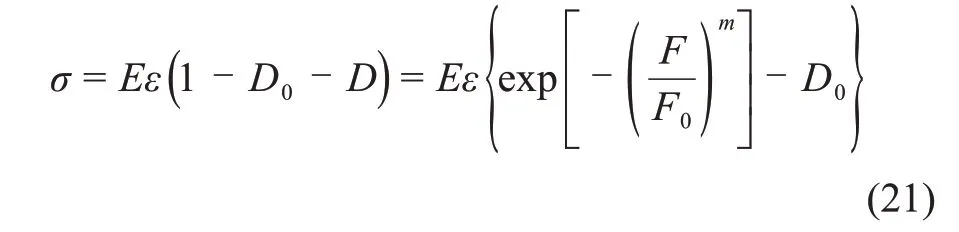
2.2 损伤本构模型参数计算
对应力-应变曲线有

由式(21)和式(22)可得:
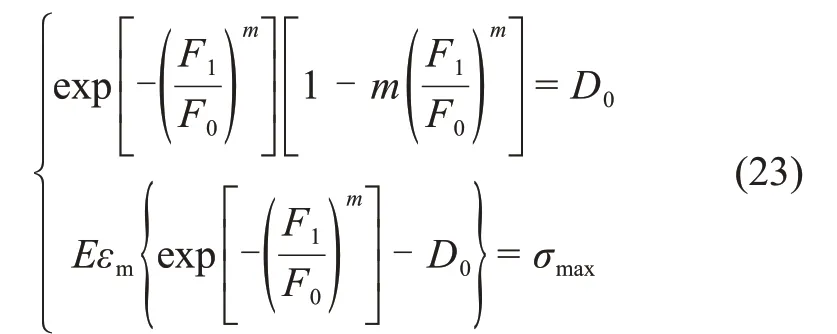
3 试验结果分析
3.1 花岗岩试样制备及力学参数
从开采自同一矿场的花岗岩中选用完整性和均质性较好的作为试样。根据岩石力学试验性能测试要求,试样直径×高为50 mm×50 mm。对每个试样两端进行打磨,保证平行度与垂直度小于0.02 mm。然后,用实测冲击力为3.49 kN、冲击频率为50 Hz、转速为1 000 r/min的电锤对花岗岩旋转冲击,形成不同直径的中心孔。花岗岩力学参数见表1。

表1 花岗岩力学参数Table1 Mechanical parameters of granite
3.2 试验设备及方案
试验采用大直径SHPB装置,入射杆与试样等截面积,以冲击的方式进行恒应变率半正弦波加载[20-21],采用DL-850E示波器及CS-1D超动态应变仪采集试验数据。试样冲击时无轴压和围压,对试样进行预冲击,调整至合适的冲击气压,用同种冲击气压冲击试样1~2 次,测得每次的应力-应变曲线,用声波检测仪测得每次冲击前、后的纵波波速。试样具体力学参数及试验结果如表2所示。
3.3 试验结果及分析
图2所示为无冲击作用时花岗岩试样的应力-应变曲线。由图2可以看出:铣削加工不同中心孔半径试样的应力-应变曲线与完整标准试样曲线的峰值强度与形状基本一致,而由表2可知:二者的纵波波速也基本相同。由此可见,在一定范围内,中心孔仅由旋转切削加工,无冲击作用时,不会对围岩产生损伤,且不受孔半径的影响。
图3所示为冲击作用下试样的应力-应变曲线,图4所示为试样峰值应力与中心孔半径的关系。由图3可知:在高频冲击作用下试样峰值应力明显下降,且其纵波波速也减小(见表2),其中试样2-1相较于试样3-1和试样4-1峰值应力下降更多,且试样3-1和试样2-1之间的峰值应力下降幅度比试样4-1和试样3-1之间的峰值应力下降幅度大,说明试样2-1产生的围岩损伤更大。当冲击载荷不变时,在一定中心孔半径范围内,随着中心孔半径减小,其产生的径向应力越大,造成的围岩损伤也越大,围岩损伤程度增大的幅度也在上升。
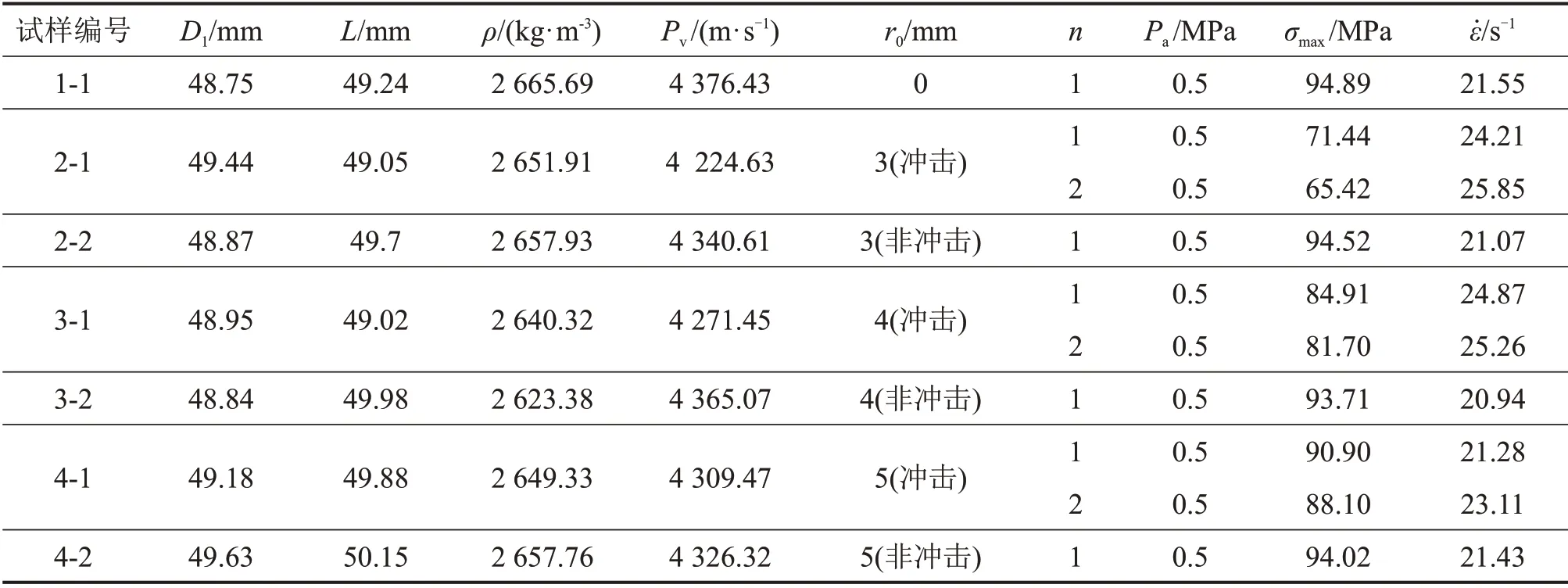
表2 花岗岩试样力学参数与试验结果Table2 Mechanical parameters and experimental results of granite specimens

图2 无冲击作用时花岗岩试样应力-应变曲线Fig.2 Stress-strain curves of granite specimens without impact loads
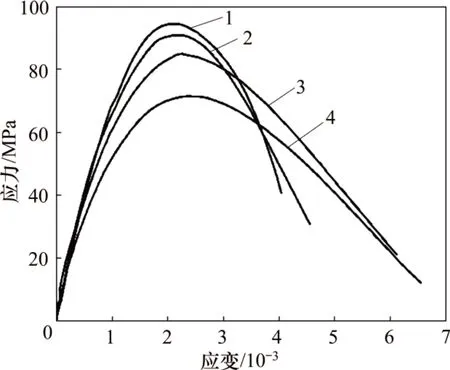
图3 冲击作用下试样应力-应变曲线Fig.3 Stress-strain curves of granite specimens under impact loads
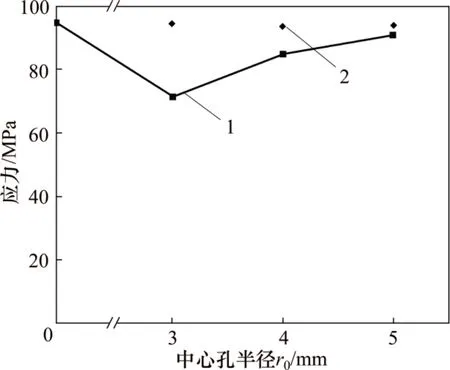
图4 试样峰值应力与中心孔半径关系Fig.4 Relationship between peak stress and center hole radius of specimens
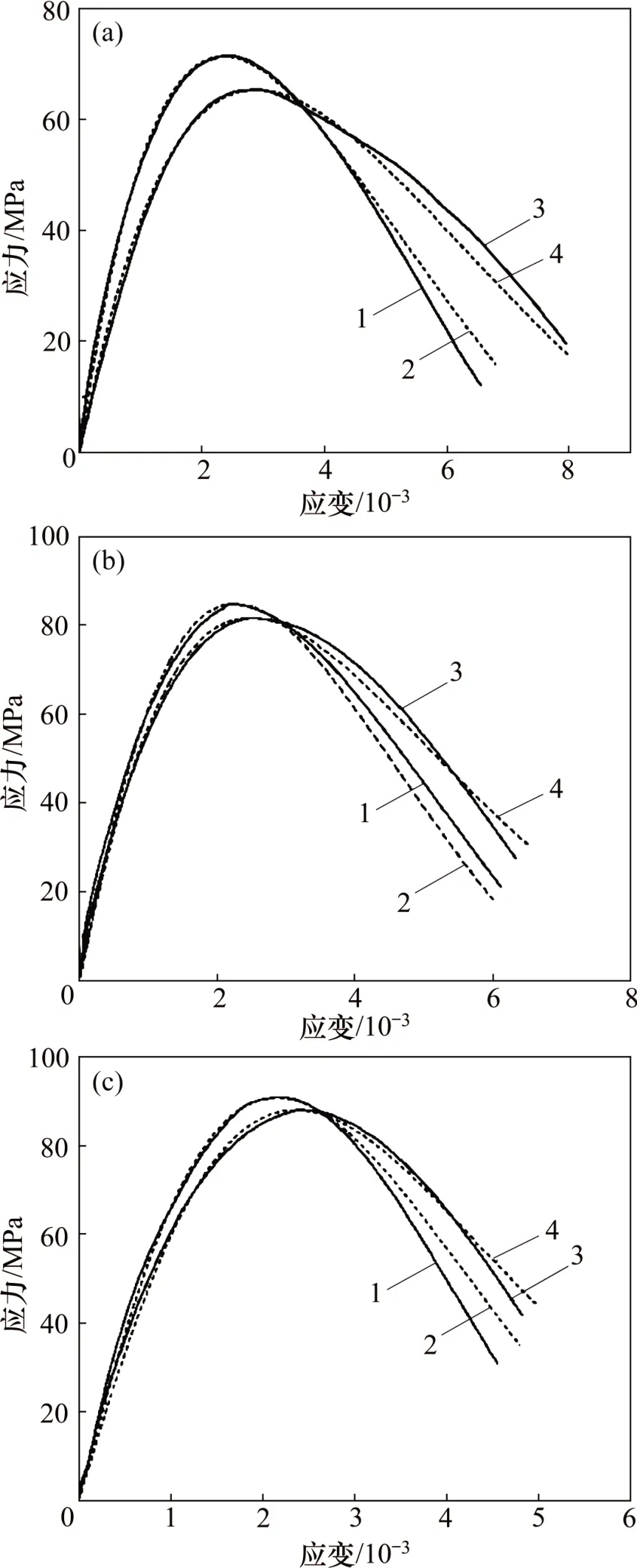
图5 冲击试样试验结果与模型计算结果对比Fig.5 Comparison of experimental and model calculation results of specimens under impact loads
图5所示为不同中心孔半径试样冲击试验结果与损伤本构模型计算结果对比。由图5可知:本构模型计算结果与试验结果有较好的一致性,说明建立的高频冲击中心孔损伤模型能够较好地反映带有围岩损伤的岩样强度与应变的关系,验证了模型的正确性。由图5还可以看出:3 种不同中心孔半径试样在第2 次冲击试验后,峰值应力均减小,且中心孔半径小的试样峰后应力-应变曲线更平缓。这意味着中心孔半径小的试样再次受到相同应力作用时,会产生更大的应变,更容易破坏。
在同一冲击载荷下,高频冲击中心孔造成的围岩损伤D0,围岩损伤区域半径与中心孔半径的比值r1/r0与中心孔半径的关系如图6所示。其中,图6(b)中的试验结果根据试验实测的纵波波速与密度通过波阻抗[22]定义的损伤公式计算得出。由图6可见:试验结果与模型计算结果相符,模型能够反映高频冲击中心孔的围岩损伤程度。从图6还可以看出:在同一冲击载荷作用下,D0和r1/r0都随中心孔半径增大而减小,且减小趋势在不断减缓;当中心孔半径增大到一定程度时,几乎不会对围岩产生损伤。对于半径较小的中心孔,同样的冲击载荷在孔壁处产生的径向应力大,可能会造成中心孔内壁围岩破坏脱落的现象,此时,减小中心孔径,损伤区域与中心孔半径比也不再明显增长。对于某一确定的冲击载荷,可得到相应的r1/r0,进而根据最终的钻孔直径确定所需的中心孔半径r0。
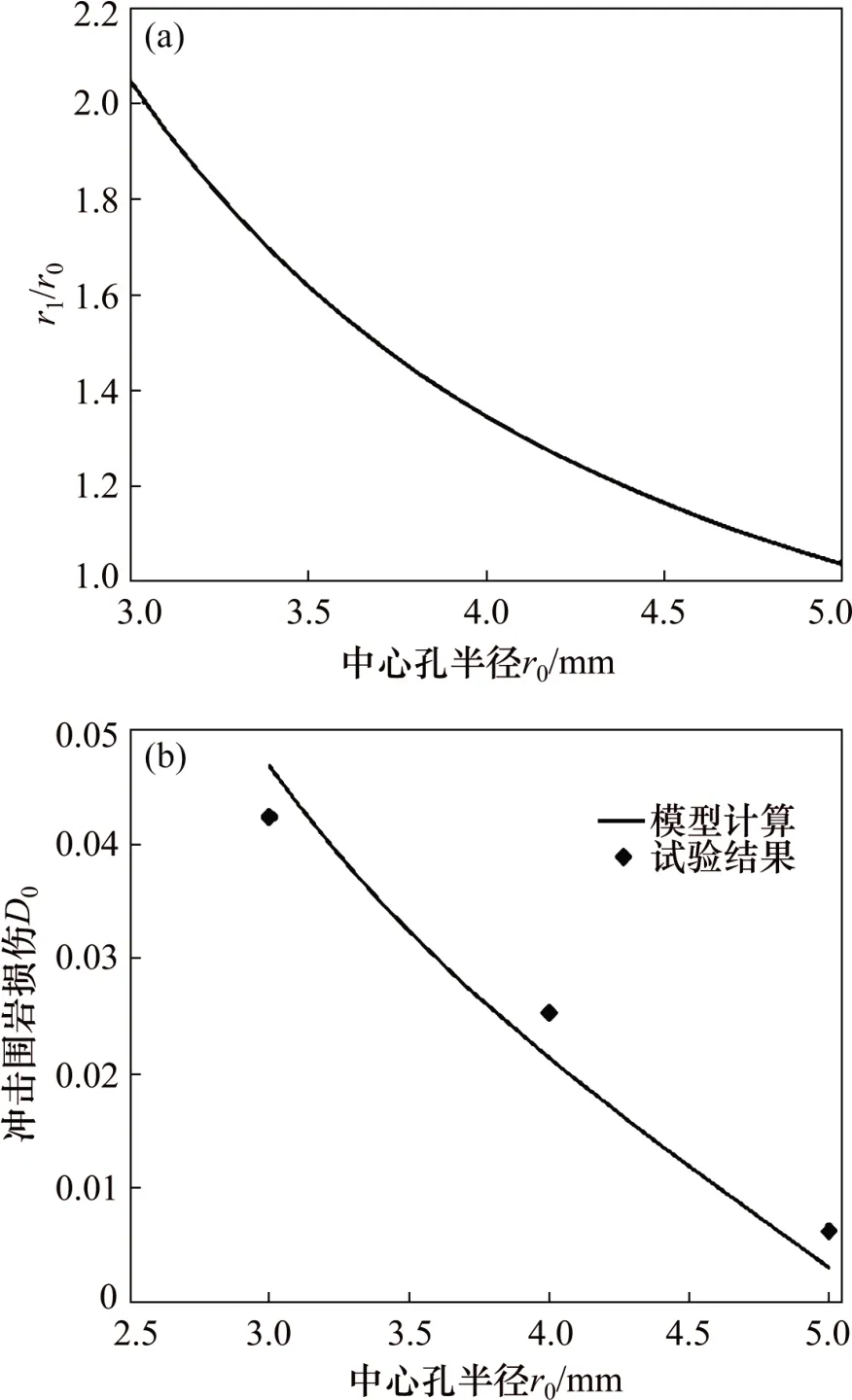
图6 r1/r0及冲击围岩损伤D0与中心孔半径r0的关系Fig.6 Relationship between r1/r0,impact damage D0 and central hole radius r0
4 结论
1)高频冲击中心孔会对围岩造成损伤;在同一冲击载荷作用下,随着中心孔半径的减小,岩样峰值应力下降,损伤区域与中心孔半径比r1/r0增大,冲击产生的围岩损伤增大;半径比的增长速率随着中心孔半径的减小而增大,当中心孔半径减小到一定值后,r1/r0不再明显增长;当冲击载荷不变时,中心孔半径r0增大到一定值后,半径比为1,不再对围岩产生损伤。
2)根据冲击载荷与建立的损伤模型得到r1/r0,进而由最终的钻孔直径确定所需的中心孔半径r0,可为复合凿岩钻具参数设计及硬岩大直径深孔采矿提供参考。
3)建立的损伤模型适应于高频冲击中心孔条件,模型计算结果与试验结果有较好的一致性;模型能够反映冲击中心孔岩样的应力、冲击围岩损伤与应变的关系,验证了模型的合理性。
