具有直接链路的能量收集认知协作中继网络中断概率分析

2019-09-18罗轶施荣华董健唐锟王雨婷

中南大学学报（自然科学版） 2019年8期

罗轶，施荣华，董健，唐锟，王雨婷

(1.中南大学信息科学与工程学院，湖南长沙，410083；2.湖南师范大学信息科学与工程学院，湖南长沙，410081)

为了解决能量受限认知中继网络(cognitive relay networks，CRNs)生存期短的问题，人们对射频能量收集(radio frequency energy harvesting，RF-EH)技术与CRNs融合形成的RF-EH-CRNs进行了研究[1-8]。区别于从主发送端(primary transmitter，PT)和/或次用户(secondary user，SU)节点的射频信号中收集能量的方式[1-4]，MONDAL 等[6-8]将功率信标(power-beacon，PB)[5]辅助RF-EH 方式引入CRNs，分别推导了多跳PB 辅助RF-EH-CRNs在无/有主网络(primary network，PN)干扰下的中断概率(outage probability，OP)。LE[8]分析了分布式多PB 辅助RF-EH-CRNs 在Nakagami-m衰落信道下的中断性能。近几年来，以机会中继选择(opportunistic relay selection，ORS)和部分中继选择(partial relay selection，PRS)这2种主动协作中继策略为基础的认知协作中继网络(cognitive cooperative relay networks，CCRNs)受到广泛关注[9-15]。但WU等[9-11]的研究中忽略了次网络(secondary network，SN)源节点和目的节点间的直接链路。SHARMA等[12]研究了采用ORS 和PRS 策略，具有单主接收端(primary receiver，PR)、中继硬件损伤和SN 直接链路的放大转发(amplify-and-forward，AF)CCRNs。MOUALEU 等[13]提出了具有单PR、单PT 和SN 直接链路的AF-CCRNs。HO-VAN[14]分析了具有单PR、单PT 和SN 直接链路的译码转发(decode- and-forward，DF)CCRNs 在采用ORS 策略及选择合并(selection combining，SC)和最大比值合并(maximum ratio combining， MRC)方式下的中断性能。而KANDELUSY 等[15]讨论了采用ORS 和PRS 策略且具有多PR、多PT和多SN目的节点以及SN直接链路的DF-CCRNs，并得出了SN 在采用SC 方式下的OP。近年来，采用RF-EH 技术和认知协作中继的EHCCRNs已成研究热点[16-18]。VERMA等[16]提出了采用携能传输的能量辅助DF-EH-CCRNs。YIN 等[17]讨论了两跳PB 辅助EH-CCRNs 在单窃听节点下的保密中断概率。而ABD-ELMAGID 等[18]则研究了具有有限中继缓存和电池容量的EH-CCRNs吞吐量。但是，以上研究均假设SN源节点和目的节点间不存在直接链路，目前对于具有SN 直接链路的PB 辅助EHCCRNs 的研究还很少。本文作者提出一种具有多PR、多SN目的节点、SN直接链路和SN硬件损伤的PB辅助DF-EH-CCRNs，并分析其在瑞利块衰落信道(Rayleigh block fading channel，RBFC)下采用ORS 策略和SC方式的SN精确和渐近中断概率。

1 网络系统模型

网络系统模型如图1所示。本文假设1个DF-EHCCRNs 模型，其中主网络由M个接收节点Qm(m∈{1,2,…,M})组成；次网络则由源节点S、N个DF 中继节点Rn和J个目的节点Dj(n∈{1,2,…,N}，j∈{1,2,…,J})组成。该模型可以表示包含几个目的节点的多用户CRNs。本文忽略主网络对次网络的干扰，模型中每个节点均为半双工方式工作的单天线设备。CCRNs 采用underlay 模式共享频谱，即S和R使用主网络授权频谱，同时通过直接链路以及选定Rn向已选定的目的节点Dj发送信息。安装了RF-EH 电路的所有R和S同时从功率信标节点B收集能量。假设所有网络链路均为独立RBFC，信道系数在一个时隙T内保持不变，而在不同时隙间独立变化[1-3]。hS,Rn，hS,Dj和hRn,Dj分别为节点S到Rn和Dj链路以及Rn到Dj链路的信道系数；fB,Rn和fB,S分别为B到Rn和S链路的信道系数；gS,Qm和gRn,Qm分别为节点S和Rn到Qm链路的信道系数。为了简单起见，与文献[1,15]类似，本文假设所有的主网络节点Q(R和D)紧靠在一起，因此S到主网络节点Q(S到R；S到D；B到R；R到Q以及R到D)链路信道增益是独立同分布的随机变量，即|hS,Rn|2，|hS,Dj|2，|hRn,Dj|2，|fB,Rn|2，|fB,S|2，|gS,Qm|2和|gRn,Qm|2分别服从期望为1/λS,R，1/λS,D，1/λR,D，1/βR，1/βS，1/ωS和1/ωR的指数分布。例如，λS,R=d ξS,R，其中dS,R为S到R的距离，ξ为路径损耗指数[1]。假设次网络节点接收端噪声为均值为0、方差为σ2的复高斯白噪声，表示为n0～CN(0,σ2)。

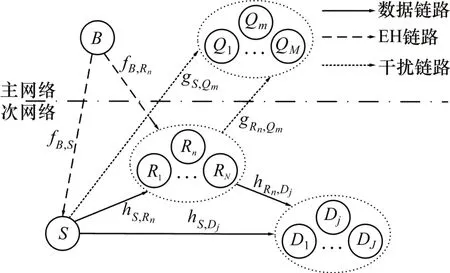
图1 网络系统模型Fig.1 Networks system model

BJORNSON 等[19]提出了一种收发信机硬件损伤模型。在该模型中，假设功率为P的信号s通过叠加了复高斯白噪声n且信道系数为h的无线信道进行传输。由于发射机和接收机的硬件损伤，导致信号s在发射和接收时产生失真。令τt和τr分别为由发射机和接收机硬件损伤导致的失真噪声，则接收端信号y可表示为

式中：τt～CN(0,k2tP)；τr～CN(0,k2rP|h|2)；参数kt和kr分别为发射机和接收机的硬件损伤水平。本文采用该模型对次网络节点的硬件损伤进行建模。为了简化分析，假设对于任意的n和j，节点S和Rn的发射机硬件损伤水平均为kt，节点Rn和Dj的接收机硬件损伤水平均为kr。

时隙结构示意图如图2所示。图2中，节点S和所有R在时隙的前αT时段(α为EH比率，0＜α＜1)同时从B收集能量，并在之后的(1-α)T时段进行数据传输(data transmission，DT)。根据文献[5]，EH 和DT所采用的信道完全分离，因此，即使Q的发射功率Pt较大，也不会对次网络和主网络产生干扰。假设节点q(q∈{S,Rn})的RF-EH电路能量转换效率均为η(0＜η＜1)，则其在EH阶段能够收集到的能量Eq为

式中：q收集到的噪声能量太小而被忽略。与文献[1,6]类似，假设q配置的大电容能存储其RF-EH电路收集到的所有能量，并且由于大电容存在漏电现象，在时隙结束时其所存储电能会被全部泄漏。

图2 时隙结构示意图Fig.2 Structural diagram of time slot

在underlay 模式下，为了确保主网络通信质量，次网络节点发射功率会受到主网络干扰约束PI的严格限制，即Q接收到的干扰信号功率不能超过PI。考虑到节点q具有硬件损伤，其发射功率Pq为

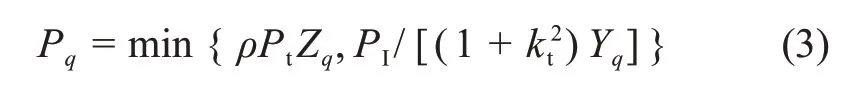
式中：Zq=|fB,q|2；Yq=max|gq,Qm|2，m=1,2,…,M；ρ= 2αη/(1 -α)，忽略电路功率消耗以及发送信息前大电容漏电所导致的能量损失。

为了降低复杂度并减少网络中传输链路信道状态信息的数据量，在节点S向D发送信息前，从节点D中选出直接链路信道质量最好的目的节点Dj*接收S和R传输的数据，其选择标准如下：

式中：j=1,2,…,J。在DT的前(1-α)T/2时段，节点S向所有的中继节点R和Dj*发送数据，Rn和Dj*的瞬时接收端信噪比γS,Rn和γS,Dj∗分别为：

式中：j=1,2,…,J。PS为节点S的发射功率；XS,Rn=|hS,Rn|2；XS,Dj=|hS,Dj|2；kt2,r=kr2+kt2。在前(1-α)T/2时段的最后，所有中继节点R对接收自节点S的数据进行译码，在随后的(1-α)T/2时段中继节点Rn将译码后的S节点数据转发给节点Dj*，则节点Dj*的瞬时接收端信噪比γRn,Dj∗为

式中：XRn,Dj∗=|hRn,Dj∗|2。

为了提高传输质量和降低系统复杂度，采用ORS策略从节点R中选出中继节点Rn*对节点Dj*进行转发，其选择标准如下：

式中：n=1,2,…,N。

在节点Dj*采用SC方式处理节点S和Rn*发送的信息，则次网络的端到端信噪比γe2e可以表示为

式中：n=1,2,…,N。

2 精确中断概率分析

中断概率是评估无线网络系统性能最重要的指标之一，本文将网络端到端的信噪比低于某一特定中断信噪比阈值γth的概率定义为中断概率(OP)。本节将推导出中断概率的精确闭合式。为了便于计算中断概率，首先推导出Yq和Uq(其中Uq=Pq/σ2，q∈{S,Rn})的累积分布函数(cumulative distribution function，CDF)和概率密度函数(probability density function，PDF)。由于Yq是M个独立同分布随机变量的最大值，其累积分布函数FYq(yq)和概率密度函数fYq(yq)分别为：

Uq的累积分布函数FUq(uq)和概率密度函数fUq(uq)分别为：

考虑到γS,Rn和γS,Dj∗存在相同随机变量US，使用条件概率将中断概率表示为

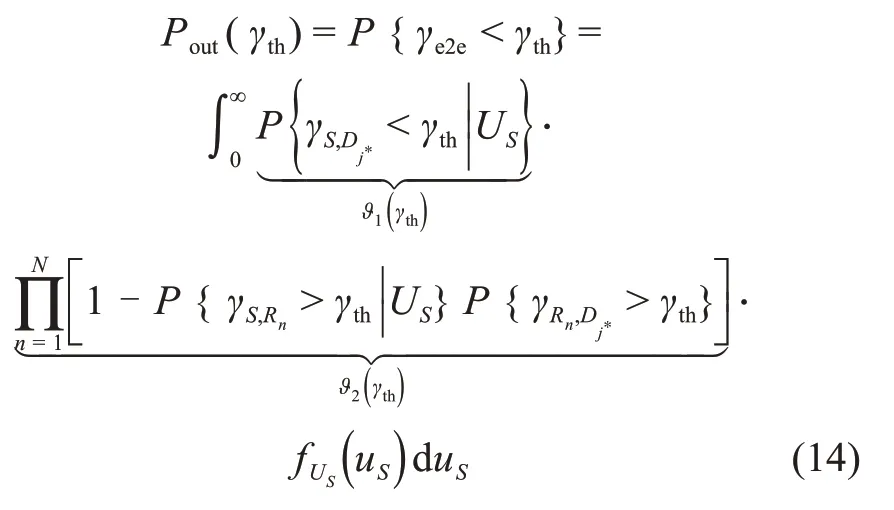
下面分别推导式(14)中的ϑ1(γth)和ϑ2(γth)。首先推导ϑ1(γth)，

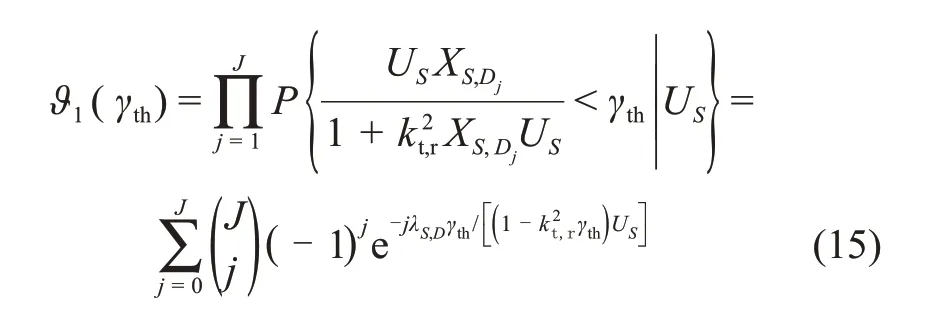
ϑ2(γth)可以表示为

依据文献[20]可得

式中：a(γth)=λR,Dγthσ2(1 +k2t)+mωRPI(1 -k2t,rγth)，K1(∙)为一阶第二类修正Bessel函数。

将式(13)，(15)和(16)代入式(14)，可得次网络精确中断概率Pout为

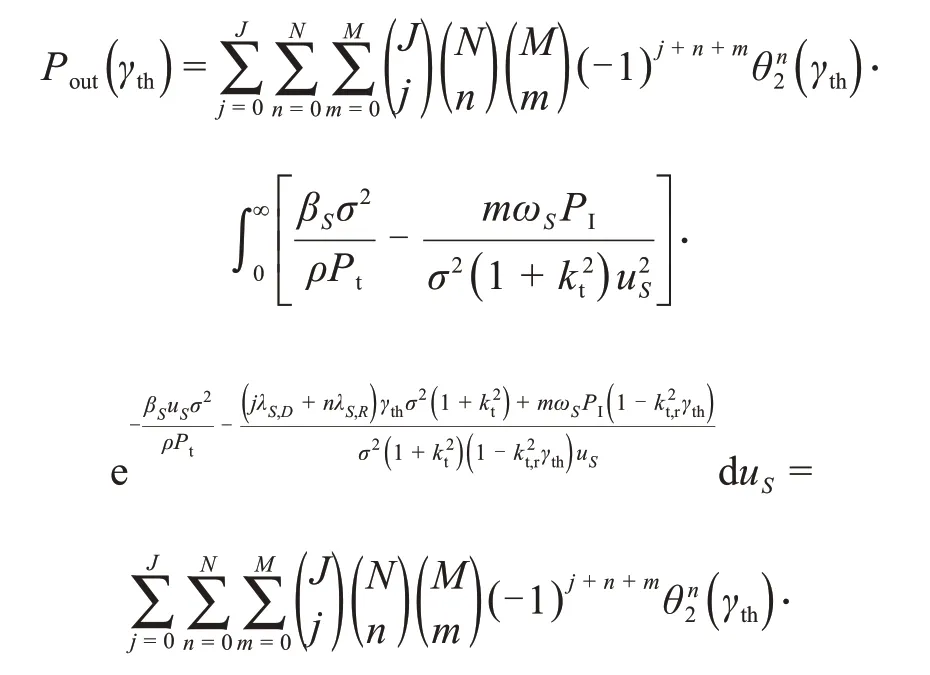
3 渐近中断概率分析

本节将分别推导在主网络对次网络无干扰限制(Pt≪PI)和有干扰限制(Pt≫PI)情况下次网络的渐近中断概率闭合式。当Pt≪PI时，主网络能容忍较大的干扰信号功率，节点q收集到的能量能全部用于发送信息；当Pt≫PI时，节点q能收集到较多能量，但其发射功率完全受PI限制。因此，在以上2 种情况下Pq(q∈{S,Rn})可分别表示为

3.1 无干扰限制下的渐近分析

当Pt≪PI时，式(5)～(7)可分别表示为

式(14)可以表示为

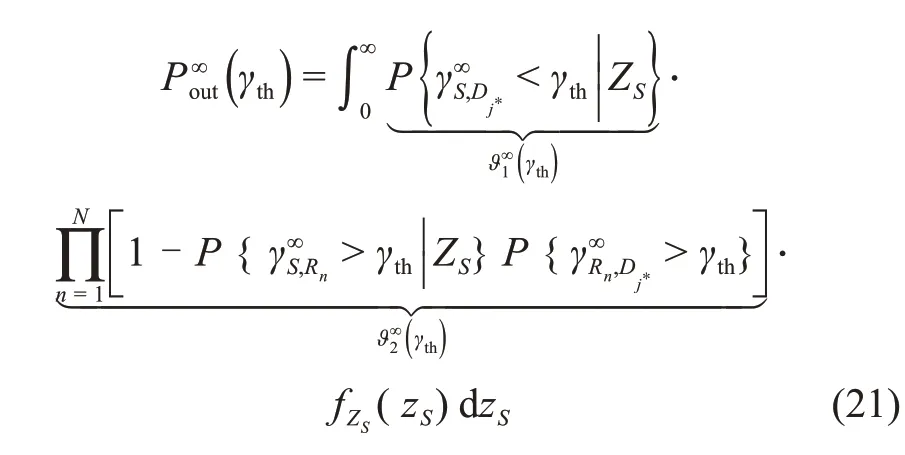
式中：ϑ∞2(γth)可以表示为

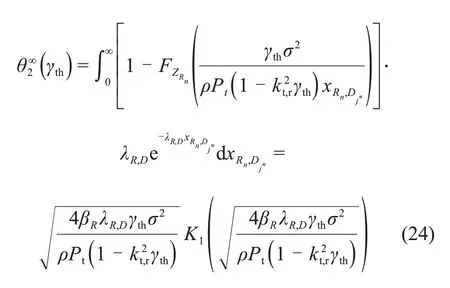
将式(22)和(23)代入式(21)，可得无干扰限制下的次网络渐近中断概率为

3.2 有干扰限制下的渐近分析

当Pt≫PI时，式(5)～(7)可分别表示为

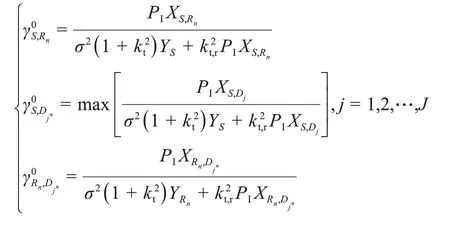
式(14)可表示为

下面分别推导式(26)中的ϑ01(γth)和ϑ02(γth)。ϑ01(γth)可以表示为

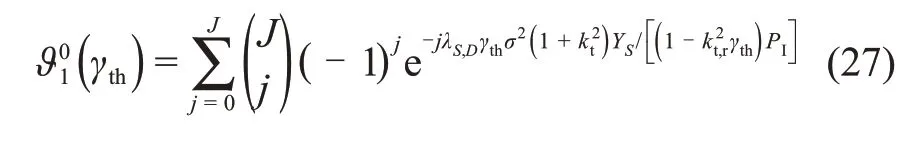
ϑ02(γth)可以表示为

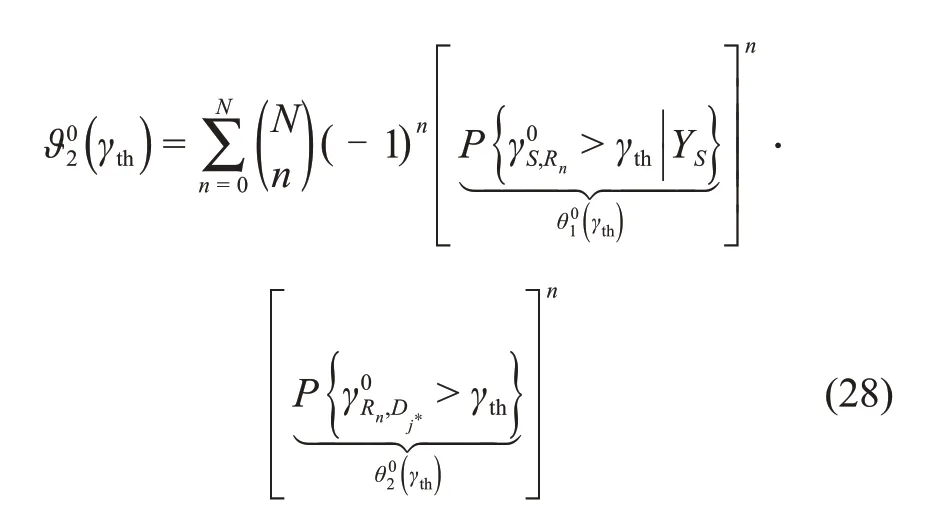
式中：d(γth)=λR,Dγthσ2(1 +k2t)。

将式(11)，(27)和(28)代入式(26)，可得有干扰限制下的次网络渐近中断概率为

从式(30)可以看出：P0out与Pt无关。一旦PI确定，Pt再大，节点q收集到的能量再多都无法使P0out下降。

4 仿真结果及分析

本节通过对中断概率理论分析的数值计算和105次Monte Carlo 仿真来分析次网络中断性能。将节点S，节点B，K个D节点，M个Q节点和N个R节点的位置分别设置在X-Y平面上的(-0.5， 0)，(-1，1)，(0.5，0)，(1.5，-0.5)和(0，1)这5 个点。在仿真分析中，中断阈值γth= 22Re2e/(1-α)- 1(其中Re2e为次网络的端到端信道容量[1])；ξ=2.5，σ2=1，Pt和PI均被σ2归一化。

当η分别为0.4 和0.8，PI分别为12 和15 dB，α=0.5，Re2e=0.85 bit/(s·Hz)，N=M=J=3，kt=kr=0.05 时，Pt与精确和渐近中断概率之间的函数关系如图3所示。从图3可见：1)给定PI和η，当Pt≪PI时，Pout与近似相等；随着Pt增大，Pout与均单调下降，且Pout逐渐大于；当Pt≫PI时，Pout将趋近于。这是因为当Pt逐步增加时，次网络节点收集到的能量随之增多，其发射功率逐渐增大，Q接收端的干扰信号功率也逐步增大到PI，此后受干扰约束限制，次网络节点的发射功率不再随Pt的增大而增加，Pout将出现饱和现象。2)给定PI和Pt，当η较大时，次网络节点能收集到较多能量以提高发射功率，从而降低Pout和。3)给定η和Pt，当PI较大时，Q能容忍次网络节点以较大发射功率传输信息，从而使Pout和降低。

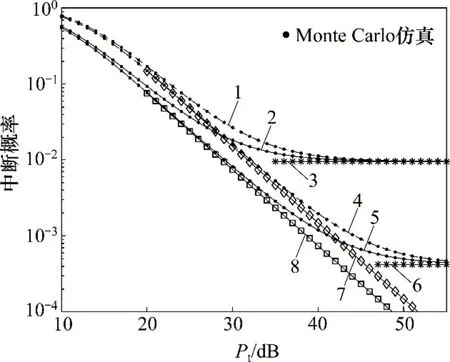
图3 Pt与中断概率之间的函数关系Fig.3 Function relation between Pt and OP

当PI=12 dB，η=0.8，α=0.5，Re2e=0.85 bit/(s·Hz)，N=M=J=3 时，次网络节点硬件损伤对中断概率的影响如图4所示。从图4可见：当Pt给定时，随着kt和kr的增大，Pout也随之增加。例如，当Pt=30 dB 时，次网络节点由无硬件损伤(kt=kr=0)变化到具有一定硬件损伤(kt=kr=0.2)后，Pout由小于1%增大到20%以上。由此可见，次网络节点硬件损伤对次网络的中断概率影响显著。

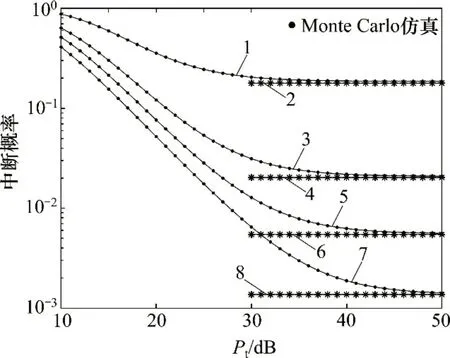
图4 硬件损伤对中断概率的影响Fig.4 Effect of hardware impairments on OP

当Pt=30 dB，η=0.8，α=0.5，Re2e=0.85 bit/(s·Hz)，kt=kr=0.05时，Q，R和D节点数对中断概率的影响分别如图5和图6所示。图5中，N=J=3，M=1,2,4,6；图6中M=3，N=J=1,2,5,10,15,20,25。从图5和图6可见：1)当N，J，M和Pt一定时，随着PI的增大，Pout单调下降并趋于饱和。这是因为次网络节点的发射功率会随PI的提升而增加，但其有限的存储能量决定了发射功率的最大值。2)给定N，J和PI，当M增大时，节点S和D到Q的干扰链路数目以及具有较大干扰信道增益的概率也随之增加，导致Pout增大。3)当M和PI给定时，增大N和J会带来更多的分集增益，从而降低Pout；但当N和J达到一定程度(如N=J＞20)后，再继续增大N和J，对Pout的降低影响很小，因此，需要合理设置N和J。

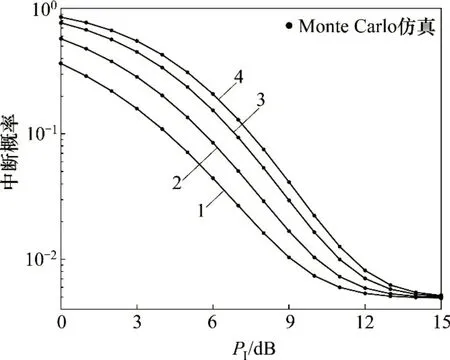
图5 主接收端Q节点数对中断概率的影响Fig.5 Effect of number of Q node on OP

图6 R和D节点数对中断概率的影响Fig.6 Effect of number of R and D nodes on OP

当Pt=15 dB，η=0.8，Re2e=0.85 bit/(s·Hz)，kt=kr=0.05，N=M=J=3 时，不同PI条件下α与中断概率Pout之间的函数关系如图7所示。从图7可见：1)当PI一定时，随着α的增加，Pout先减小再逐步增大。这是因为随着α从0开始逐渐增大，次网络节点能收集到更多能量用于提高发射功率，致使Pout降低；随着α的持续增大，γth随之增加，但次网络节点发射功率受PI限制不再升高，导致Pout上升。2)当PI取不同值时，Pout最小值所对应的α也不尽相同。例如，当PI=7 dB时，α取0.2可使Pout最小；当PI=10 dB时，α取0.3可使Pout最小；而当PI≥15 dB时，α取0.4可使Pout最小。因此，恰当设置α能有效降低Pout。